В этом материале я хочу сделать подробный обзор такого понятия, как «перплексия» («коэффициент неопределённости»), так как оно применяется в обработке текстов на естественном языке (Natural Language Processing, NLP). Я расскажу о двух подходах, которые обычно используются для определения этого понятия, и о тех идеях, которые лежат в основе этих подходов.

1. Пара слов о том, что такое языковые модели
Если вы хорошо знаете о том, что такое языковые модели, можете пропустить этот раздел.
Языковая модель — это статистическая модель, которая назначает вероятности словам и предложениям. Обычно такие модели используются для того, чтобы предсказать следующее слово w в предложении, учитывая все предыдущие слова, часто называемые «историей». Например, исходя из истории «For dinner I’m making __», какова вероятность того, что следующим словом будет «cement»? Какова вероятность того, что следующим словом будет «fajitas»?
Будем надеяться, что P(fajitas|For dinner I’m making) > P(cement|For dinner I’m making).
Тех, кто использует такие модели, кроме того, часто интересуют вероятности, которые эти модели назначают целым предложениям W, составленным из последовательностей слов (w_1,w_2,…,w_N).
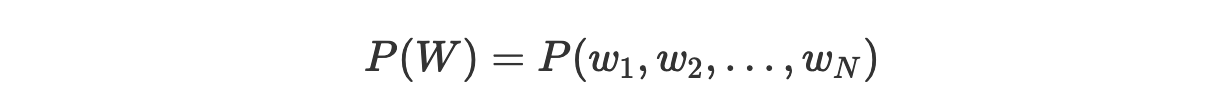
Предположим, нам нужна модель, умеющая назначать более высокие вероятности настоящим, синтаксически корректным предложениям.
Униграммная модель (unigram model) работает лишь на уровне отдельных слов. Такая модель, получив последовательность слов W, выдаст следующую вероятность:

Здесь отдельные вероятности P(w_i) могут быть, например, определены на основе частоты появления слов в обучающем множестве.
А вот N-граммная модель (n-gram model) вместо этого учитывает и предыдущие (n-1) слов для оценки вероятности появления следующего слова. Например, триграммная модель будет интересоваться предыдущими 2 словами. В результате получаем следующее:


Языковые модели могут встраиваться в более сложные системы в виде вспомогательных средств для решения различных языковых задач, таких, как перевод с одного языка на другой, классификация текстов, распознавание речи и так далее.
2. Оценка языковых моделей
Перплексия — это метрика, используемая для оценки языковых моделей. Зачем она может понадобиться? Почему нельзя просто оценить потери/точность итоговой системы на интересующей нас задаче?
На самом деле, можно использовать два различных подхода для оценки и сравнения языковых моделей:
-
Внешняя оценка. Тут применяется оценивание модели путём решения с её помощи задачи, на которую она рассчитана (например, задачи машинного перевода текстов), и анализ итоговых показателей потерь/точности. Это лучший подход к оцениванию моделей, так как это — единственный способ реально оценить то, как разные модели справляются с интересующей нас задачей. Но реализация этого подхода может потребовать больших вычислительных мощностей, его применение может оказаться медленным, так как для этого нужно обучение всей анализируемой системы.
-
Внутренняя оценка. Тут используется подход, предусматривающий поиск некоей метрики для оценки самих языковых моделей, без учёта конкретных задач, для решения которых их планируется использовать. Хотя внутренняя оценка моделей не так «хороша», как внешняя, если речь идёт об итоговой оценке модели, она являет собой полезное средство для быстрого сравнения моделей. Вычисление перплексии — это метод внутренней оценки моделей.
3. Перплексия как обратная вероятность тестового набора, нормализованная по количеству слов

Это, видимо, определение перплексии, которое встречается чаще всего. Здесь мы поговорим о смысле этого определения.
3.1. Вероятность тестового набора
Для начала подумаем о том, что собой представляет хорошая языковая модель. Как уже было сказано, нам нужно, чтобы наша модель назначала бы высокие вероятности настоящим, синтаксически корректным предложениям, а предложениям ненастоящим, некорректным, или очень редко встречающимся — низкие вероятности. При условии, что наш набор данных состоит из настоящих и корректных предложений, это значит, что лучшей моделью будет та, которая назначит наивысшую вероятность этому тестовому набору. Интуитивно понятно то, что если модель назначает высокую вероятность тестовому набору, это означает, что её этот набор не удивляет (она не приведена им в недоумение, не «перплексирована»), а это значит, что данная модель обладает хорошим пониманием того, как устроен язык.
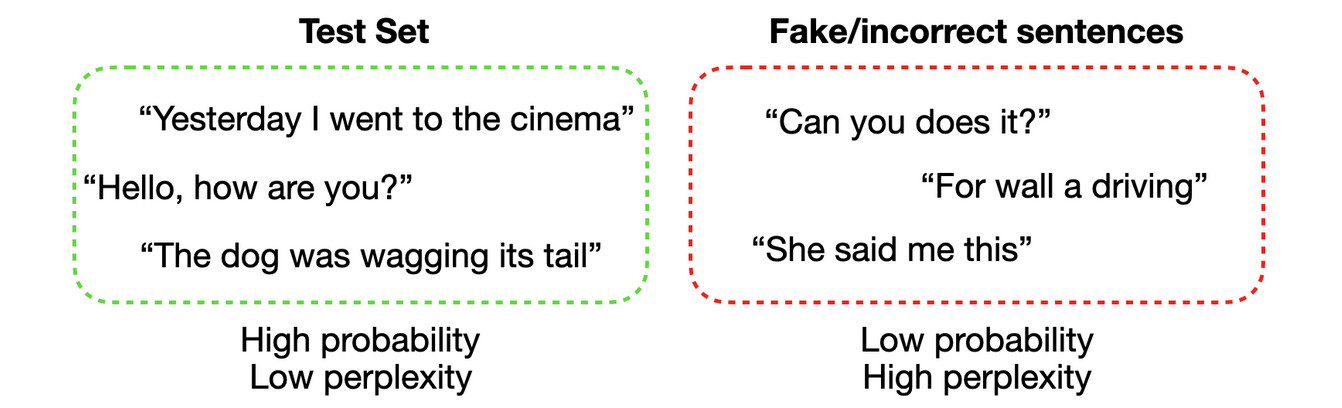
3.2. Нормализация
Тестовый набор, высокая вероятность, низкий уровень перплексии. Ненастоящие или неправильные предложения, низкая вероятность, высокий уровень перплексии
Стоит упомянуть о том, что наборы данных могут состоять из различного количества предложений, а сами предложения могут состоять из различного количества слов. Ясно то, что добавление в набор данных большего количества предложений ведёт к росту уровня неопределённости. В результате, при прочих равных условиях, у большего тестового набора вероятность, скорее всего, будет меньше, чем у меньшего. Нам, в идеале, хотелось бы иметь метрику, независимую от размера набора данных. Получить её можно, нормализовав вероятность тестового набора по общему количеству слов, что даст показатель, соответствующий одному слову.
Как это сделать? Если то, что мы хотим нормализовать, представляет собой сумму неких параметров, мы просто можем поделить эту сумму на количество слов и получить значение, соответствующее одному слову. Но вероятность последовательности слов вычисляется не путём сложения параметров, а путём их умножения. Возьмём, например, униграммную модель:

Как нормализовать эту вероятность? Это несложно сделать, если обратиться к логарифмической вероятности, что позволяет преобразовать произведение показателей в сумму:

Теперь полученный показатель можно нормализовать, разделив его на N и получив логарифмическую вероятность для одного слова:
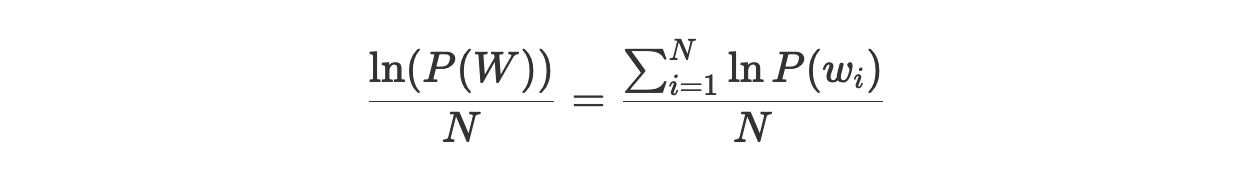
После этого от логарифма можно избавиться, прибегнув к операции возведения в степень:

Тут можно видеть, что мы выполнили нормализацию путём взятия из показателя корня N-й степени.
3.3. Собираем всё вместе
Теперь, возвращаясь к исходному уравнению перплексии, мы можем интерпретировать этот показатель как обратную вероятность тестового набора, нормализованную по количеству слов в тестовом наборе:
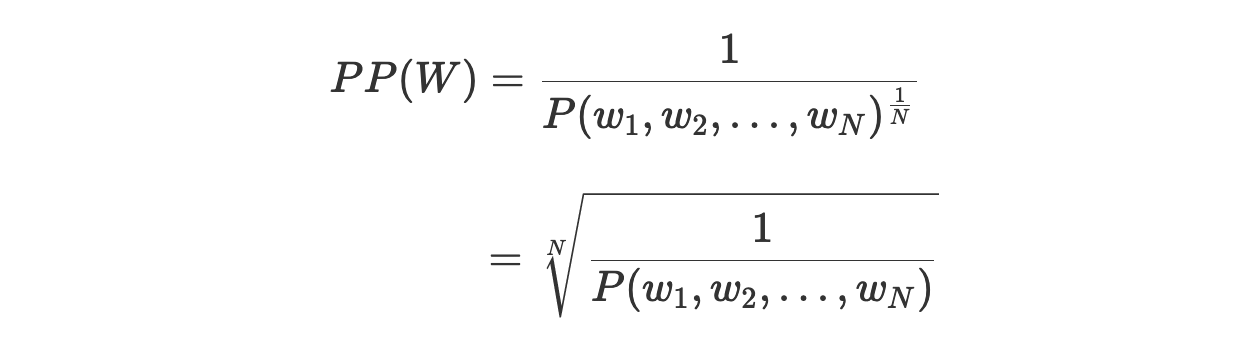
Обратите внимание на следующее.
То, что мы получаем обратную вероятность, означает, что чем ниже уровень перплексии — тем лучше модель.
В данном случае W — это тестовый набор. Он содержит, одно за другим, слова из всех предложений, включая токены начала (start-of-sentence, ) и конца (end-of-sentence, ) предложения.
Например, тестовый набор, состоящий из двух предложений, будет выглядеть так:
W = (<SOS>, This, is, the, first, sentence, . ,<EOS>,<SOS>,This, is, the, second, one, . ,<EOS>)N — это количество всех токенов в тестовом наборе, включая SOS/EOS и знаки препинания. В данном примере N = 16.
Если нужно — можно посчитать перплексию для отдельного предложения. В таком случае W будет представлять собой это предложение.
4. Перплексия как результат возведения 2 в степень, соответствующую показателю перекрёстной энтропии
Если вам нужно освежить знания об энтропии — я от всего сердца рекомендую взглянуть на этот материал.
Перплексию, кроме того, можно определить как результат возведения 2 в степень, соответствующую показателю перекрёстной энтропии:
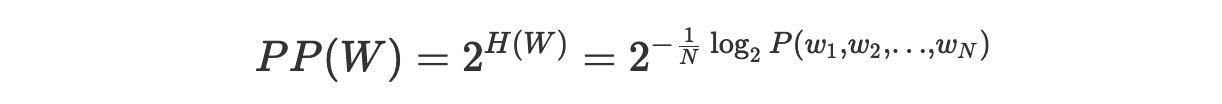
Мы сразу же можем доказать то, что это определение эквивалентно предыдущему:
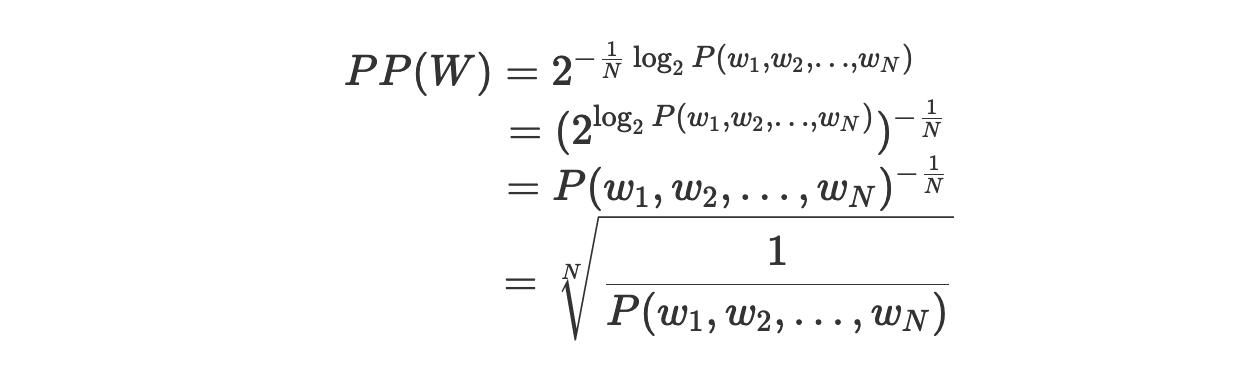
Как объяснить это определение, опираясь на понятие перекрёстной энтропии?
4.1. Перекрёстная энтропия языковой модели
Мы знаем о том, что энтропию можно интерпретировать как среднее количество битов, необходимое для хранения информации в переменной. Представить её можно так:
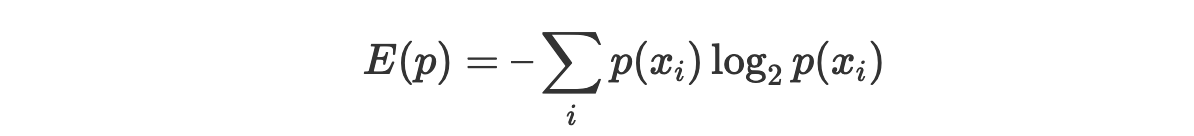
Нам известно и то, что кросс-энтропию можно представить так:
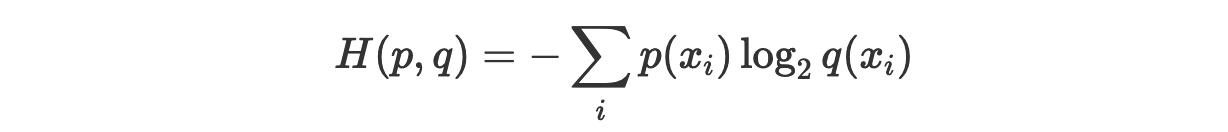
Это может быть интерпретировано как среднее количество битов, необходимое для хранения информации в переменной в том случае, если вместо реального распределения вероятности p мы используем предполагаемое распределение q.
В нашем случае p — это реальное распределение нашего языка, а q — это распределение, основанное на предположении, сделанном моделью на основании обучающего множества. Вполне очевидно то, что мы не можем знать реального распределения p, но, взяв достаточно длинное предложение W, состоящее из слов (то есть — используя большой показатель N), мы можем приблизительно определить кросс-энтропию для одного слова, используя теорему Шеннона–Макмиллана–Бреймана (подробнее об этом можно почитать здесь и здесь):
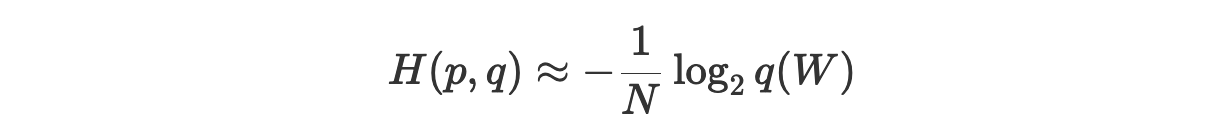
Перепишем эту формулу так, чтобы её форма соответствовала той, которую мы использовали в предыдущем разделе. Имея последовательность слов W длины N и обученную языковую модель P, мы можем приблизительно определить кросс-энтропию так:
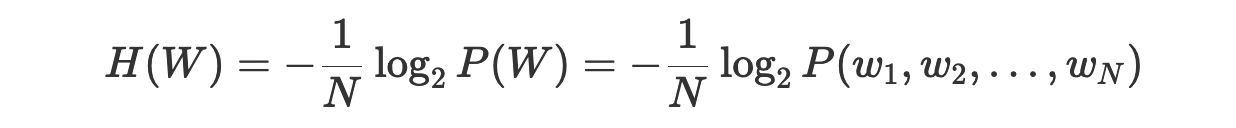
Давайте вспомним наше определение перплексии:
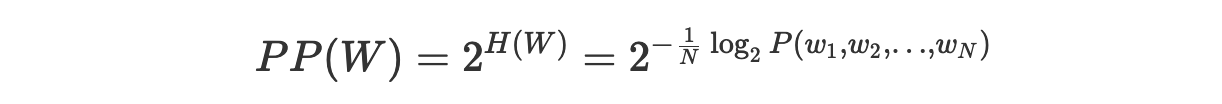
Основываясь на том, что мы знаем о кросс-энтропии, мы можем сказать, что H(W) — это среднее количество битов, необходимое для кодирования каждого слова. Это означает, что перплексия 2^H(W) — это среднее количество слов, которое может быть закодировано с использованием H(W) битов.
Как это интерпретировать? Перплексию можно рассматривать как взвешенный коэффициент ветвления.
4.2. Взвешенный коэффициент ветвления: бросаем игральную кость
Итак, выше мы сказали следующее:
-
H(W)— это среднее количество битов, необходимое для кодирования одного слова. -
2^H(W)— это среднее количество слов, которое может быть закодировано с использованиемH(W)битов.
Если мы, например, выясним, что H(W) = 2, это будет означать, что для кодирования каждого слова, в среднем, нужно 2 бита. А используя 2 бита, мы можем закодировать 4 слова.

Но что это значит? Давайте, ради упрощения нашей задачи, ненадолго забудем о языке и о словах, и представим, что наша модель, на самом деле, пытается предсказать результат бросания игральной кости. У обычной кости имеется 6 граней, в результате коэффициент ветвления для игральной кости равен 6. Коэффициент ветвления — показатель довольно-таки простой: он указывает на то, сколько возможных исходов может быть у каждого броска игральной кости.

Предположим, что мы обучаем модель на такой вот правильной кости. Модель учится тому, что каждый раз, когда мы бросаем кость, вероятность выпадения любой из сторон равняется 1/6. Далее, предположим, что мы создаём тестовый набор, бросая кость 10 раз, после чего получаем следующую последовательность исходов, весьма незамысловатую: T = {1, 2, 3, 4, 5, 6, 1, 2, 3, 4}. Какова перплексия этого набора данных?

Получается, что перплексия совпадает с коэффициентом ветвления.
Представим теперь, что у нас имеется неправильная игральная кость. Вероятность выпадения числа 6 равняется 7/12, а остальные числа выпадают с вероятностью 1/12 каждое. Мы снова обучаем модель, на этот раз — на учебном наборе данных, который создан с использованием этой неправильной игральной кости. В результате модель изучает именно эти вероятности. Затем мы создаём новый тестовый набор T, бросая кость 12 раз, получая 6 в 7 бросках, а в оставшихся 5 — другие цифры. Каким теперь является показатель перплексии?

Теперь этот показатель меньше, чем в прошлый раз. Это так из-за того, что модель знает о том, что выпадение 6 более вероятно, чем выпадение любого другого числа. В итоге модель меньше «удивляется», увидев 6, а так как в тестовом наборе шестёрок больше, чем других чисел, то общее «удивление», связанное с тестовым набором, оказывается меньшим. Коэффициент ветвления, как и прежде, равняется 6, так как любой бросок, как и ранее, может завершиться выпадением любого числа. А вот взвешенный коэффициент ветвления теперь ниже, причиной чего является тот факт, что выпадение одной из сторон кости более вероятно, чем выпадение других. Это можно попытаться описать так: при каждом броске кости наша модель так же не уверена в исходе, как если бы ей надо было бы выбирать между 4 разными вариантами, в противовес выбору между 6 вариантами в том случае, когда каждая сторона кубика может выпасть с одинаковой вероятностью.

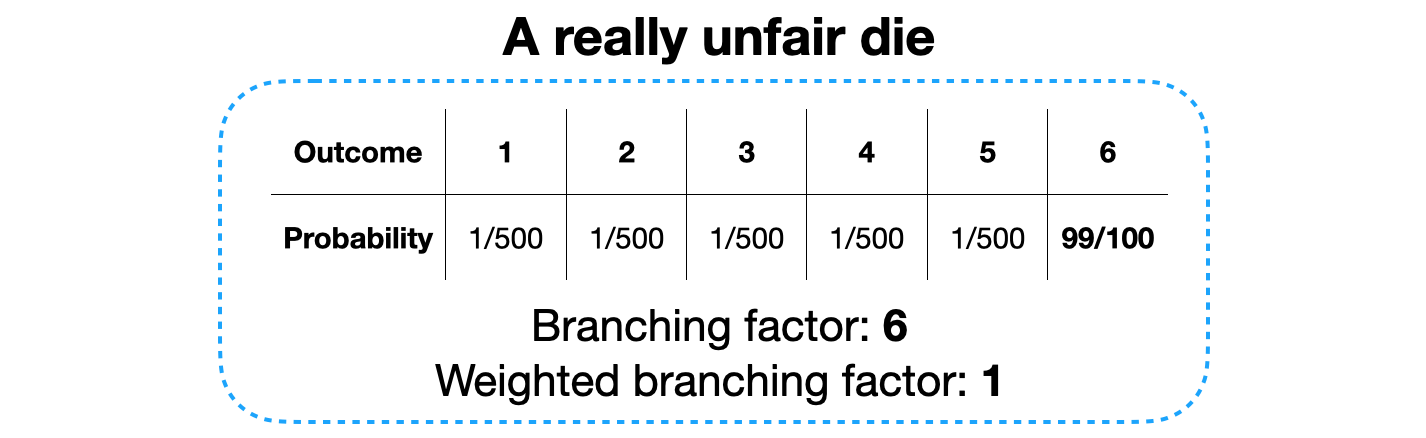
Для того чтобы ещё лучше во всём этом разобраться — давайте доведём наш пример до крайности. А именно — предположим, что у нас имеется очень неправильная кость, при броске которой 6 выпадает с вероятностью 99%, а другие числа — с вероятностью 1/500 каждое. Мы, как и прежде, обучаем модель с использованием этой игральной кости, а потом создаём тестовый набор, бросив кость 100 раз. Число 6 выпало 99 раз, а какое-то другое число — лишь один раз. Вот какой теперь будет перплексия:
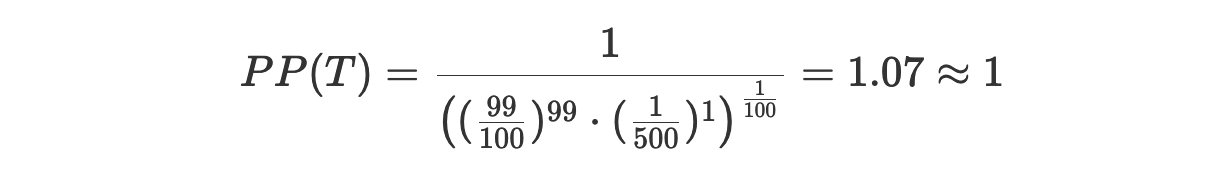
Коэффициент ветвления по-прежнему равняется 6, а вот взвешенный коэффициент ветвления теперь равняется 1, так как модель почти полностью уверена в том, что результатом каждого броска будет 6, и эта её уверенность совершенно обоснована. И хотя, с технической точки зрения, каждый бросок может закончиться любым из 6 исходов, есть лишь один исход, который появляется почти при каждом броске.
4.3. Взвешенный коэффициент ветвления: языковые модели
А теперь давайте применим то, о чём мы только что говорили, к языковым моделям и к кросс-энтропии.
Для начала надо сказать, что если у нас имеется языковая модель, пытающаяся предсказать следующее слово, её коэффициент ветвления — это просто количество слов, появление которых возможно в каждой из позиций, а это — всего лишь размер словаря.
Ранее мы говорили, что перплексия в языковой модели — это среднее количество слов, которое можно закодировать, используя H(W) битов. Теперь мы видим, что это значение всего лишь представляет собой средний коэффициент ветвления модели. Как уже было сказано, если мы выяснили, что значение кросс-энтропии равняется 2, то это указывает на показатель перплексии, равный 4, представляющий собой «среднее количество слов, которое может быть закодировано», а это — всего лишь средний коэффициент ветвления. Всё это значит, что, когда мы пытаемся предсказать следующее слово, наша модель так же «растеряна», как если бы ей пришлось выбирать между 4 различными словами.
5. Итоги
Перплексия — это метрика, используемая для оценки качества модели.
Перплексию можно определить как обратную вероятность тестового набора, нормализованную по количеству слов:
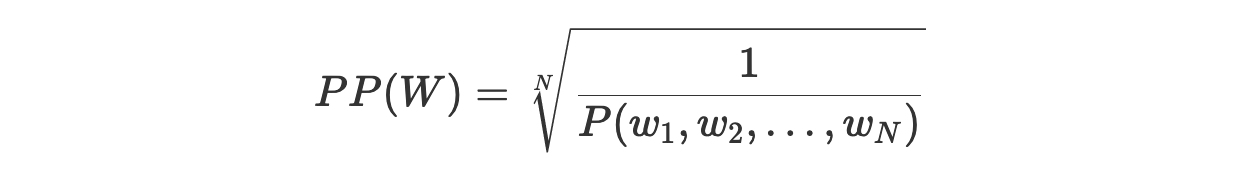
Альтернативный способ определения перплексии заключается в использовании кросс-энтропии, в то время как кросс-энтропия указывает на среднее количество битов, необходимых для кодирования одного слова, а перплексия — это количество слов, которое может быть закодировано с помощью этих битов:
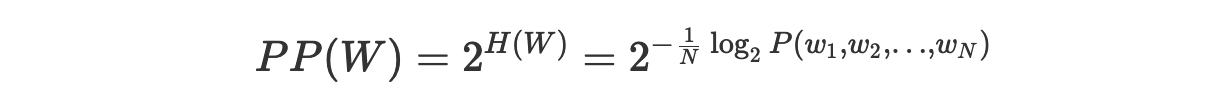
Перплексию можно интерпретировать как взвешенный коэффициент ветвления. Например, если показатель перплексии равен 100, это означает, что когда модели приходится предсказывать следующее слово, это приводит модель в такую же «растерянность», как если бы ей пришлось выбирать одно из 100 слов.
Вот полезные англоязычные материалы по теме:
-
Jurafsky, D. and Martin, J. H. Speech and Language Processing. Chapter 3: N-gram Language Models (2019).
-
Koehn, P. Language Modeling (II): Smoothing and Back-Off (2006). Data Intensive Linguistics
-
Vajapeyam, S. Understanding Shannon’s Entropy metric for Information (2014).
-
Iacobelli, F. Perplexity (2015)
-
Lascarides, A. Language Models: Evaluation and Smoothing (2020). Foundations of Natural Language Processing (Lecture slides)
-
Mao, L. Entropy, Perplexity and Its Applications (2019). Lei Mao’s Log Book
О, а приходите к нам работать? 😏
Мы в wunderfund.io занимаемся высокочастотной алготорговлей с 2014 года. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.
Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.
Сейчас мы ищем плюсовиков, питонистов, дата-инженеров и мл-рисерчеров.
Присоединяйтесь к нашей команде.
Комментариев нет:
Отправить комментарий