В прошлой статье я описал алгоритм, позволяющий строить более интересные (в противовес более коротким, как делают всякие яндексы-гуглы) пешеходные маршруты между двумя точками. Алгоритм загружал достопримечательности, парки и прочие приятные и интересные для пешеходов объекты из Open Street Map и прокладывал маршрут через них. В итоге путь мог оказаться на 10-20% длиннее, но гораздо живописнее и интереснее.

Фото города — Alex 'Florstein' Fedorov
В комментариях многие написали, что кроме маршрутов между двумя точками им интересно было бы строить круговые маршруты, которые бы начинались и заканчивались в одной и той же точке и укладывались в заданный лимит времени. Например, если у вас есть два часа до поезда или до встречи с друзьями, съездить куда-то далеко вы за это время не успеете, а вот погулять и посмотреть красоты поблизости вполне можно.
После некоторого количества экспериментов я сочинил генетический алгоритм, который строит достаточно неплохие (для меня) маршруты в такой ситуации. Под катом описание принципа работы и несколько примеров.
Итак, пользователи хотят иметь возможность совершить небольшой тур по окрестностям и вернуться обратно в точку начала за указанное время (обычно 1-2 часа). Как оказалось, такой тип прогулок довольно востребован. Например, в статье "Movement patterns of tourists within a destination" описано исследование треков 250 туристов в Гонконге, при этом 40% туристов начинали знакомство с городом с кругового маршрута в радиусе 500 метров от отеля. Однако
зачастую люди просто бродят вокруг, не зная что интересного можно увидеть поблизости.
Задача осложняется, если дело происходит не в туристическом центре (где куда ни пойди — везде найдешь что-то интересное), а где-нибудь на окраине, где достопримечательности надо искать.
Радиус и отбор достопримечательностей
Для построения маршрута нам сперва надо отобрать достопримечательности, которые мы хотим посетить. А для этого нужно определить область их поиска вокруг стартовой точки. Если пользователем определено максимальное время прогулки в M минут, то максимально удаленной точкой, до которой можно дойти и успеть вернуться, будет точка на расстоянии (V * M / 2), где V – скорость пешехода.
Средней предпочитаемой скоростью пешехода можно считать 1.4 метра в секунду. Однако при осмотре достопримечательностей человек идет несколько медленнее, так как тратит дополнительное время на осмотр. Я построил немного маршрутов по городу и погулял по ним, сравнивая хронометраж прогулки с тем, что предсказывало приложение. В результате оказалось, что средняя прогулочная скорость моя оказалась примерно на 20% меньше, т.е. примерно 1.1 м/с. Так как я периодически останавливался чтобы пофотографировать, свериться с картой, иногда лишний раз переходил дорогу чтобы выбрать лучший ракурс или купить мороженого.

Эксперименты я проводил в незнакомых районах города, с помощью моего алгоритма там можно найти всякие интересные штуки про которые раньше и не слышал. Вот, например, памятник первой листовке.
Выбор достопримечательности на максимальном расстоянии приведет к построению вырожденного кругового маршрута. Поскольку у пешехода уже не будет времени сходить с кратчайшего пути по прямой, он сможет посетить только эту достопримечательность, пройдя к ней и вернувшись обратно по той же улице, как показано красной стрелкой.
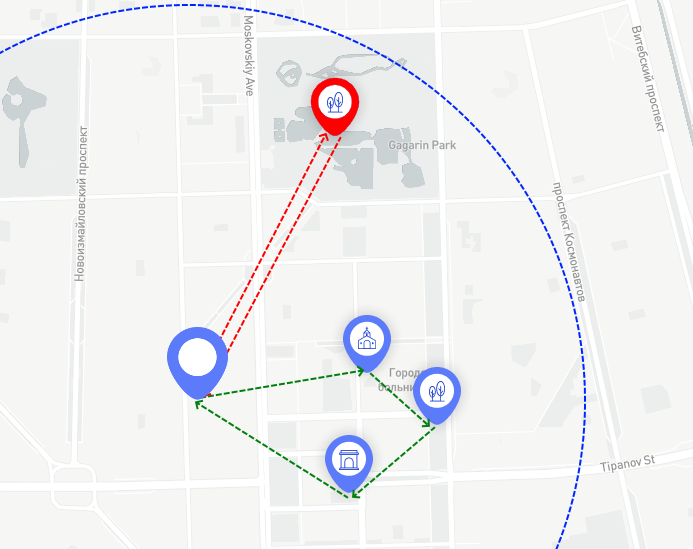
Тут мы можем или сходить в парк подальше, или посетить сразу несколько точек поближе
Но такая ситуация противоречит идее интересных круговых маршрутов, ведь по сути мы увидели только одну улицу и один объект, а хочется посмотреть побольше всего. Поэтому по результатам экспериментов был выбран радиус равный одной трети максимального расстояния. При таком радиусе поиска у пешехода хватит времени дойти до самой удаленной достопримечательности по радиусу, затем при необходимости пройти такое же расстояние по хорде в поисках других интересных объектов, и затем вовремя вернуться.
Проблемы лобового подхода
Окей, список достопримечательностей-кандидатов мы собрали. Осталось теперь выбрать, какие из них и в каком порядке мы хотим осмотреть. Посетить их все мы, скорее всего, не успеем, так что надо выбрать самое интересное их подмножество.
Сперва я попробовал сформулировать и построить обычный последовательный алгоритм. Однако быстро наткнулся на ряд проблем.
Если рассмотреть ситуацию с рисунка выше, то непонятно откуда начинать строить маршрут. Если парк — самая важная, но самая удаленная достопримечательность, то начав с нее мы получим вырожденный вариант, о котором писали раньше.
Следующее очевидное решение — как-то кластеризовать достопримечательности и пытаться искать путь до самого выгодного кластера, а затем ходить внутри него. Но тут опять все непонятно: с какого кластера начинать, в какую сторону идти. Всегда можно попасть в ловушку типа что мы пошли не в ту сторону и уперлись в "пустыню" — область без достопримечательностей, которую нам уже не хватит времени перейти и вернуться в стартовую точку.
В какой-то момент мне стало понятно, что я практически выполняю работу генетического алгоритма: рисую на карте разные маршруты и пытаюсь определить, насколько они понравились бы лично мне.
Генетический алгоритм
Получив пронумерованный список достопримечательностей, алгоритм должен выбрать упорядоченное подмножество, которое и составит основу кругового маршрута. Итоговый маршрут в таком случае является одним из размещений множества ключевых достопримечательностей (мы не хотим повторов и не обязаны использовать все возможные объекты).
Зная формулу для количества размещений из n по k можно прикинуть возможное количество вариантов. Если рассматривать часовой маршрут вокруг Дворцовой площади в Санкт-Петербурге, в радиусе 1320 метров (который определен, как описано выше) после фильтрации и кластеризации окажется 54 кандидата в ключевые достопримечательности.
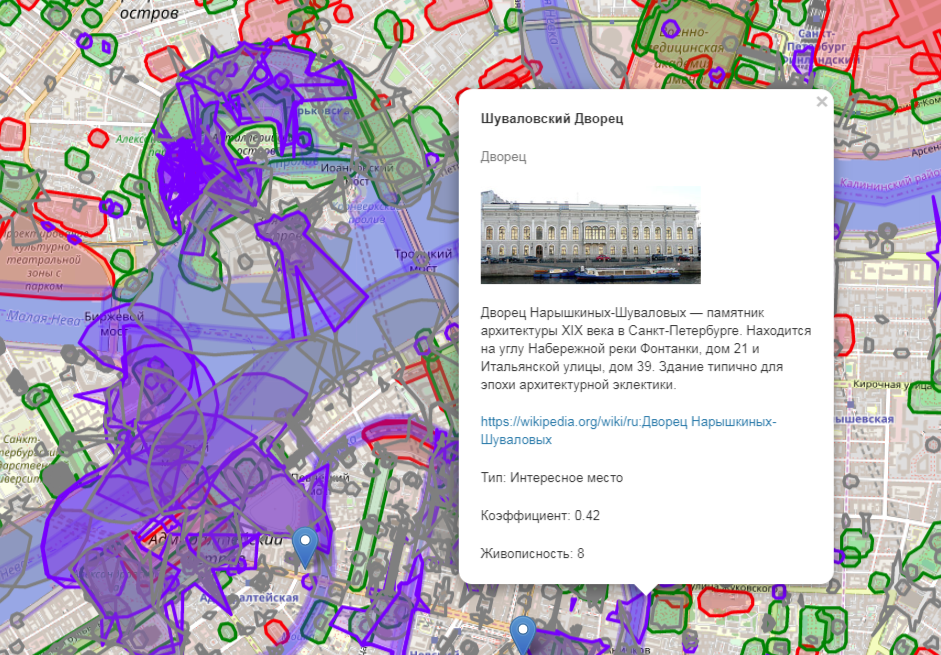
Адская каша из кучи достопримечательностей в центре, дебажный вывод областей видимости, рассчитанных по алгоритму из прошлой статьи
Принцип отбора и сортировки описан в прошлой статье, плюс мы дополнительно удаляем объекты с интересностью меньше 3 (ради таких незначительных объектов человек вряд ли будет готов далеко идти, разве что рядом вообще больше ничего нет). Таким образом возможное число маршрутов можно вычислить по формуле числа размещений из 54 по 5, оно равно 379501200. Для 2 часового маршрута, в радиус которого попадает уже 151 достопримечательность, это количество будет равняться 73423236600. Ну так, многовато для простого перебора.
Хромосомы и генетические операторы
Хромосомы в данном случае представляют собой строку, в которой каждый элемент – номер соответствующей ключевой достопримечательности. Для подобных задач, в которых хромосомы являются перестановками или размещениями, существуют специальные оптимизированные варианты генетических операторов. Такие операторы сохраняют свойство хромосомы оставаться перестановкой или размещением начального множества элементов.
- Для скрещивания используется Partially-Mapped Crossover (PMX).
- Для мутации используется обмен местами двух случайных генов (Swap Mutator).
Описание работы этих операторов с примерами можно найти, например, в работе "Genetic algorithms for the travelling salesman problem: A review of representations and operators".
Фитнес-функция
Фитнес-функция должна учитывать следующие факторы для построения интересного кругового маршрута:
- Суммарная интересность всех посещенных ключевых достопримечательностей должна быть как можно больше.
- Суммарное время в пути должно быть как можно ближе к заданному пользователем, маршрут не должен быть ни сильно длиннее, ни сильно короче. Короткие маршруты допустимы лишь тогда, когда поблизости нет достаточного количества достопримечательностей.
- Маршрут не должен пересекать сам себя. За каждое самопересечение мы добавляем штрафные проценты к итоговому значению функции.
- Форма маршрута должна быть приближена к кругу, он должен захватывать как можно большую область города и избегать вырожденных случаев. Для этого мы в функцию закладываем отношение площади фигуры, описанной маршрутом, к площади круга, в котором искались достопримечательности.
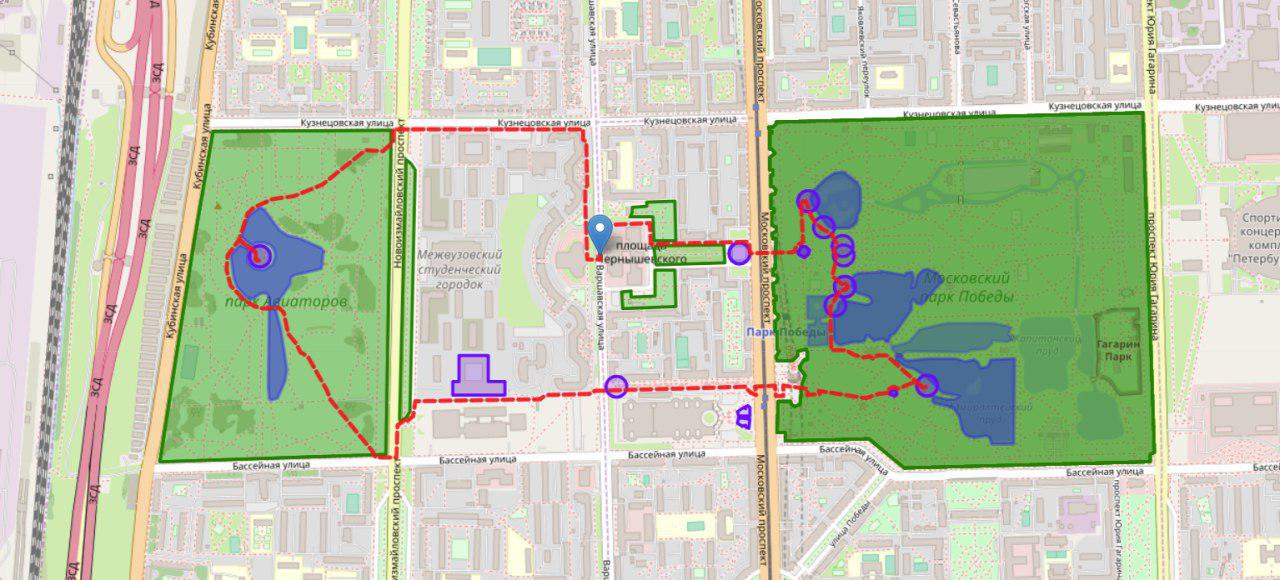
Вот пример хорошего кругового маршрута. Он проходит через два парка и нигде не посещает одно и то же место дважды
А вот пример явно неудачного маршрута. Он содержит тупиковые ответвления, где пешеходу придется возвращаться уже по осмотренной дорожке назад, и самопересечения. В местах пересечений обычно напрасно тратится время на повторный осмотр уже увиденных участков города.
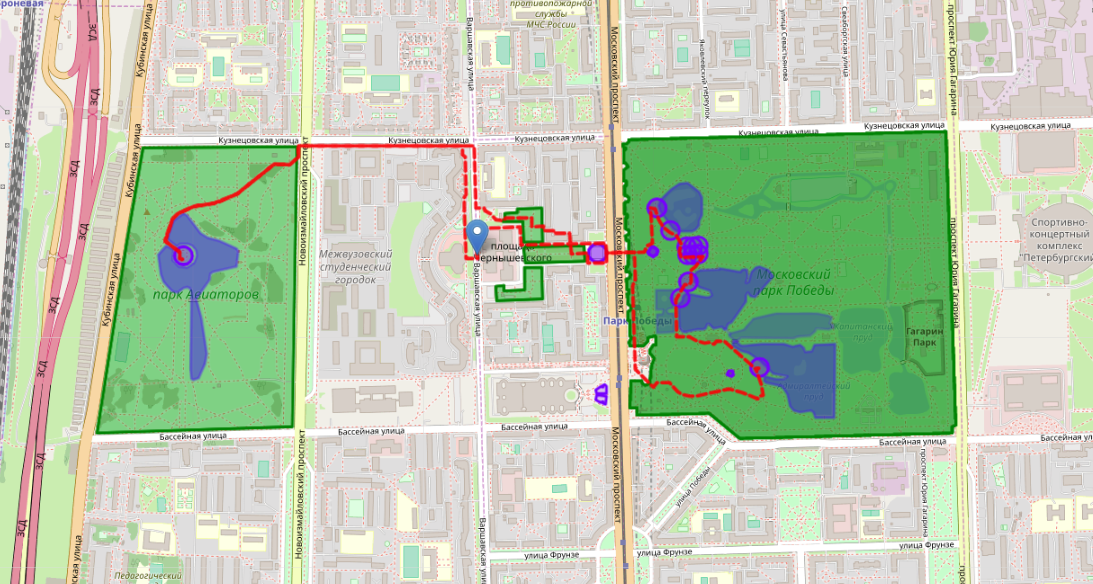
Плохой маршрут собственно был получен генетикой, в которой у фитнес-фунции были отключены пункты 3 и 4 (штрафы за самопересечения и за маленькую площадь)
Нюансы
Во время тестирования всплыли еще некоторые нюансы.
Превышение лимита времени
Во время работы генетики для ускорения длину маршрута мы считаем по прямым линиям между точками. А после того, как мы с помощью генетического алгоритма выбрали объекты для связи, путь между ними мы ищем алгоритмом из прошлой статьи. При этом путь может стать длиннее и вылезти за лимит времени. Ведь в городе часто кратчайший путь по улице может быть в разы длиннее прямой линии.
В среднем разница обычно около 10-20% и мы ее закладываем в фитнес-функцию (т.е. генетика ищет маршрут с запасом по времени, который затем съедается при прокладке детального маршрута). Иногда ее не хватает — приходится пересчитывать маршрут заново. Есть у нас в городах такие вот места, где разница между маршрутами "как птица" и "как пешеход" составляет километры.
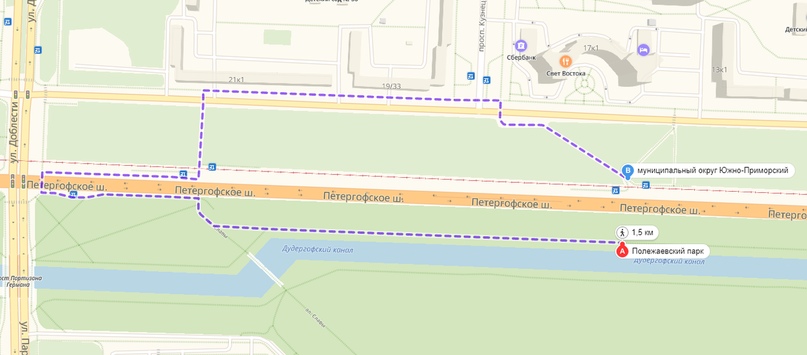
Между точками 50 метров по прямой, но полтора километра по тротуарам и переходам в обход.
Впрочем все равно алгоритм иногда превышает заданное пользователем время, но тут уж каждый сам может решить — есть ли у него лишних 10-15 минут или прогулку придется завершить пораньше.
Венеция
Когда алгоритм был готов, я для интереса решил добавить топовые туристические города Европы. Получилось интересно: города везде разные, особенности картографирования в OSM тоже, в итоге постоянно приходилось что-то допиливать.
Конкретно поиск круговых маршрутов сломался на Венеции. Так как это уникальный пример города с несвязанными областями — острова разделены Гранд-каналом, через который нет мостов, переправа возможно только на паромах.

В итоге алгоритм отбирал часть объектов с одной стороны от пролива, часть — с другой, затем не мог найти между ними сухопутного пути и падал. Пришлось добавить проверку на достижимость всех достопримечательностей из стартовой точки.
Иногда все-таки приходится возвращаться той же дорогой
В примере с парком выше есть кусочек маршрута, где придется возвращаться назад той же дорогой — это маленький полуостров, на котором стоит памятник с самолетом. На этот полуостров ведет единственная дорожка, по ней же придется и вернуться. Так что полностью запрещать такие возвраты нельзя. Алгоритм для этого повышает веса всех ребер, которые уже были пройдены, снижая вероятность возврата по ним, но все-таки делает это возможным.
Хотя иногда это все равно плохо работает. Например жалуются на главный кафедральный собор в Калининграде. Он находится на острове посередине реки, через который идет мост. С этого моста один спуск и одна дорожка к собору, видимо алгоритм слишком уж повышает веса этого единственного пути, что делает невыгодным возврат по нему. В итоге в собор он почти никогда маршрут не заводит, хоть это и одна из ключевых достопримечательностей города. Тут еще требуется какая-то доработка.
Результаты
Генетический алгоритм — штука немного непредсказуемая, поэтому иногда он глючит и рисует странные зигзаги. Но в целом результатом я доволен. Что особенно приятно, алгоритм работает не только в туристическом центре (где и так не проблема интересно провести время), но и на окраинах города. Где, зачастую, без подсказок найти что-то интересное очень сложно.
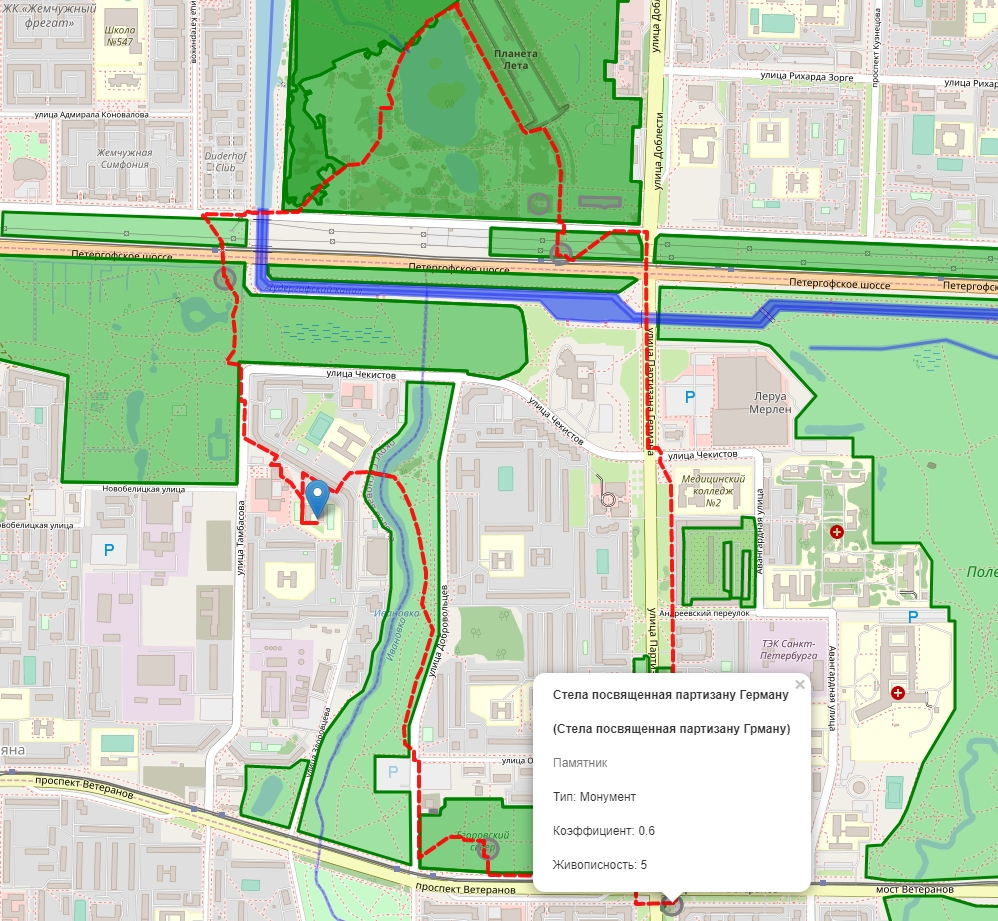
Даже в спальниках юго-запада можно найти достаточно памятников на двухчасовую прогулку
Попробовать алгоритм самостоятельно в одном из 77 поддерживаемых городов можно на нашем сайте https://sightsafari.city или в нашем Android-приложении (да-да, мы наконец-то его доделали).
Особенно интересно, как будет алгоритм работать в городах со сложным рельефом и перепадами высот. Мы добавили поддержку анализа рельефа к библиотеке поиска путей Graphopper, но проверить как следует не можем — Питер слишком ровный город.
В общем пробуйте, пишите отзывы, правильно ли строятся маршруты. Тут же можно оставить заявку на добавление новых городов.
Комментариев нет:
Отправить комментарий