Парсер Хабра: Кватернионы. Решение одной навигационной задачи

суббота, 3 апреля 2021 г.

Кватернионы. Решение одной навигационной задачи

История

Некоторое время назад я занимался одной интересной задачей, относящейся к спутниковой навигации. Используя фазовый фронт сигнала, объект навигации (ОНВ) измеряет координаты навигационных спутников (НС) в своей системе координат (локальная система, ЛСК). Также ОНВ получает значения положений НС в глобальной системе координат (ГСК), и измеряет время получения сигнала НС (рис. 1). Требовалось вычислить координаты ОНВ в ГСК и системное время, то есть решить навигационную задачу.

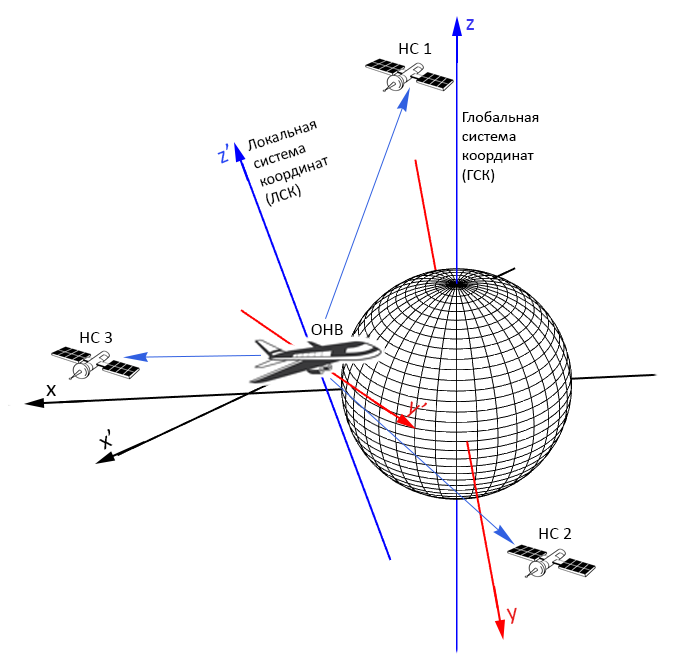
Задача была интересна тем, что её решение теоретически позволяет уменьшить число НС в сравнении с тем, сколько НС требуется в методах, реализованных в спутниковых системах навигации. Своё внимание в то время я в основном уделял исследованию качества измерений фазового фронта и получению навигационных уравнений для координат и времени, полагая при этом, что вычисление ориентации и координат ОНВ не вызовет особых проблем. Тем более, что на плоскости задача решалась быстро и просто.

Однако, когда я построил модель в трёхмерном пространстве, неожиданно выяснилось, что вычислить значения ориентации ОНВ при неизвестных его координатах в ГСК не получается. Несколько предпринятых попыток определить ориентацию с помощью матриц направляющих косинусов и поворотов привели к такому нагромождению тригонометрических функций, что продвигаться дальше к решению у меня не получалось. Какое-то время даже казалось, что аналитического решения вообще не существует.

Но оно, конечно, существует. Мне удалось найти решение этой задачи, используя свойства кватернионов. В этом материале я хочу описать саму задачу, ход и её решение, уделяя внимание ориентации и координатам ОНВ, и пока оставляя за рамками измерения координат по фазовому фронту.

Входные данные

Итак, входные данные:

$\mathbf R_i = \begin{bmatrix} x_i & y_i & z_i \end{bmatrix}^T$ : вектор-столбец положения -го НС в ГСК, i = 1, 2, 3 : номер НС,
$\mathbf R_i ^{'} = \begin{bmatrix} x_i^{'} & y_i^{'} & z_i^{'} \end{bmatrix}^T$ : вектор-столбец положения -го НС в координатах ЛСК; векторы $\mathbf R_i$ и $\mathbf R_i^{'}$ полагаем известными; ГСК, ЛСК: правые декартовы системы координат в 3-х мерном евклидовом пространстве E^3 с разнонаправленными базисами $(\mathbf e_x, \mathbf e_y, \mathbf e_z)$ и $( \mathbf e_x^{'}, \mathbf e_y^{'}, \mathbf e_z^{'})$ соответственно; начала координат ГСК и ЛСК не совпадают. Нижний индекс дальше будет обозначать номер вектора, верхний - номер элемента в векторе, если только не указано явно, что это степень.

Задача

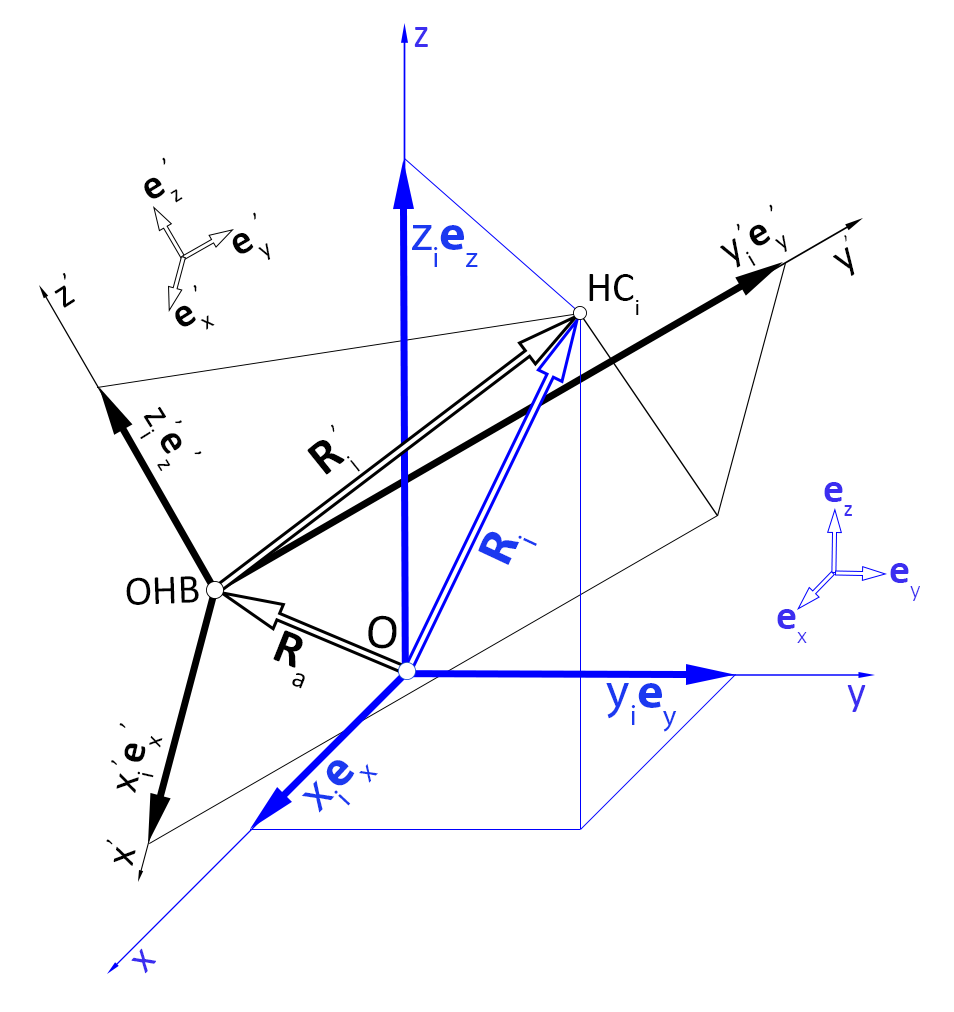
Нужно найти:

$\mathbf R_a = \begin{bmatrix} x_a & y_a & z_a \end{bmatrix}^T$ : вектор-столбец положения ОНВ в ГСК,

$\mathbf M$ : оператор перехода от ЛСК к ГСК, который я условно назвал "оператором ориентации" (рис. 2)

Решение

Теперь ход моих рассуждений и решения.

Разложение векторов $\mathbf R_i$ и $\mathbf R_i^{'}$ в своих базисах: $\mathbf R_i = x_i \mathbf e_x + y_i \mathbf e_y + z_i \mathbf e_z,\quad \mathbf R_i^{'} = x_i^{'} \mathbf e_x^{'} + y_i^{i} \mathbf e_y^{'} + z_i^{'} \mathbf e_z^{'}$ , где i=1,2,3 - номер НС. Базисные векторы ЛСК

$\begin{cases} \mathbf e_x^{'} = a_1^1 \mathbf e_x + a_1^2 \mathbf e_y + a_1^3 \mathbf e_z,\\ \mathbf e_y^{'} = a_2^1 \mathbf e_x + a_2^2 \mathbf e_y + a_2^3 \mathbf e_z,\\ \mathbf e_z^{'} = a_3^1 \mathbf e_x + a_3^2 \mathbf e_y + a_3^3 \mathbf e_z, \end{cases}$

где $\lbrace a_j^i: a_j^i \in \mathcal R \rbrace$ , $\mathcal R$ - множество вещественных чисел, i = 1, 2, 3 . Выписывая эти коэффициенты в матрицу

$\mathbf M = \begin{bmatrix} a_1^1 & a_2^1 & a_3^1\\ a_1^2 & a_2^2 & a_3^2\\ a_1^3 & a_2^3 & a_3^3 \end{bmatrix},$

получаем

$\mathbf e_x^{'} = \mathbf M \mathbf e_x,\; \mathbf e_y^{'} = \mathbf M \mathbf e_y,\; \mathbf e_z^{'} = \mathbf M \mathbf e_z,\;$

полагая, что $\mathbf e_x = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}^T$ , $\mathbf e_y = \begin{bmatrix} 0 & 1 & 0 \end{bmatrix}^T$ , $\mathbf e_z = \begin{bmatrix} 0 & 0 & 1 \end{bmatrix}^T$ . Следовательно, координаты вектора $\mathbf R_i^{'}$ в базисе ГСК $\mathbf R_i^{''} = \mathbf M \mathbf R_i^{'}$ . Можно сказать, что $\mathbf M$ является матрицей некоторого линейного оператора (или "оператора ориентации"), такого, что $E^3 \to E^3$ , определённого в базисе ГСК. Такой матрицей может быть матрица направляющих косинусов или любая из матриц поворотов.

Свойства произвольного евклидового пространства позволяют записать уравнение для вычисления вектора положения ОНВ:

$\mathbf R_a = \mathbf R_i - \mathbf M \mathbf R_i^{'}.$ (1)

Неудачный поиск решения

Уравнение (1) содержит две неизвестные матричные величины $\mathbf R_a$ и $\mathbf M$ , и имеет поэтому бесконечное число решений. Аналогичное соотношение для трёх различных НС в виде

$\mathbf R = \mathbf R_a + \mathbf M \mathbf R^{'},\qquad (2)$

где

$\mathbf R = \begin{bmatrix} x_1 & x_2 & x_3\\ y_1 & y_2 & y_3\\ z_1 & z_2 & z_3 \end{bmatrix},\quad \mathbf R_1 = \begin{bmatrix} x_1^{'} & x_2^{'} & x_3^{'}\\ y_1^{'} & y_2^{'} & y_3^{'}\\ z_1^{'} & z_2^{'} & z_3 ^ {'} \end{bmatrix} -$

квадратные невырожденные матрицы, также содержат две неизвестные матричные величины $\mathbf R_a$ и $\mathbf M$ . Можно переписать (1) и (2) так, чтобы избавиться от величины $\mathbf R_a$ :

$\mathbf R_a = \mathbf R_i - \mathbf M \mathbf R_i^{'} = \mathbf R_k - \mathbf M \mathbf R_k^{'},\quad i \ne k;\quad i,k=1,2,3,$

откуда

$(x_k^{'} - x_i^{'}) \mathbf M \mathbf e_x + (y_k^{'} - y_i^{'}) \mathbf M \mathbf e_y + (z_k^{'} - z_i^{'}) \mathbf M \mathbf e_z =\\ = (x_k - x_i) \mathbf M \mathbf e_x + (y_k - y_i) \mathbf M \mathbf e_y + (z_k - z_i) \mathbf M \mathbf e_z,$

или

$\mathbf M \mathbf R_{ki}^{'} = \mathbf R_{ki}, \qquad (3)$

где $\mathbf R_{ki}^{'} = \mathbf R_k^{'} - \mathbf R_i^{'}$ .

Если бы я смог как-нибудь найти $\mathbf M$ из (3) и подставить в (1), то задача была бы решена. К примеру, была сделана попытка расписать (3) по трём НС аналогично с (2), но в итоге матрицы получались вырожденные и уравнение единственного решения поэтому не имело. Попытки расписать и решить систему уравнение вроде

$\begin{cases} \mathbf M \mathbf R_{12}^{'} = \mathbf R_{12},\\ \mathbf M \mathbf R_{13}^{'} = \mathbf R_{13} , \end{cases} \qquad (4)$

приводили к тому самому нагромождению синусов и косинусов, о котором я упомянул во вступлении.

Здесь я и подумал, а получится ли найти $\mathbf M$ , если (3) или (4) записать в кватернионном виде. В итоге получилось, но продолжу по порядку.

Теория о кватернионе поворота

Два теоретических момента, которые, думаю, стоит упомянуть.

Кватернионом, как мы знаем, является математический объект вида $\dot q = q^0 + iq^1 + jq^2 + kq^3 = q^0 + \dot{ \mathbf q}$ , где q^0 , q^1 , q^2 , q^3 $\in \mathcal R$ , q^0 - скалярная часть (множитель вещественной единицы), $\dot{\mathbf q}$ - векторная часть; 1, i, j, k - вещественная и три разные мнимые единицы с таблицей умножения:

$\begin{split} 1^2 = 1,\quad 1i = i1,\quad 1j = j1,\quad 1k = k1,\quad i^2 = j^2 = k^2 = -1,\\ ij = -ji = k,\quad jk = -kj = i,\quad ki = -ik = j. \end{split}$

Кватернион даёт удобную возможность представления трёхмерных преобразований (вращений), определяя одновременно и ось поворота, и угол вращения. Если взять некоторый кватернион $\dot q = q^0 + \dot{\mathbf q} = q^0 + iq^1 + jq^2 + kq^3$ , такой, что $\Vert \dot q \Vert = 1$ , то можно записать, что $\Vert \dot q \Vert = q^{(0)^2} + \Vert \dot {\mathbf q } \Vert = 1$ , и значит $\Vert \dot q \Vert = \cos^2 \gamma + \sin^2 \gamma = 1$ , где $\cos^2 \gamma = q^{(0)^2}$ , $\sin^2 \gamma = \Vert \dot { \mathbf q} \Vert = q^{(1)^2} + q^{(2)^2} + q^{(3)^2}$ . Здесь индекс в скобках обозначает номер элемента, а верхний индекс без скобки - возведение в степень. Если вектор $\dot { \mathbf q}$ представить как

$\mathbf{ \dot q} = \frac{1}{\Vert \dot {\mathbf q} \Vert} (q^{(1)^2} + q^{(2)^2} + q^{(3)^2}) \Vert \dot {\mathbf q} \Vert = (q^{(x)^2} + q^{(y)^2} + q^{(z)^2}) \Vert \dot {\mathbf q} \Vert = (q^{(x)^2} + q^{(y)^2} + q^{(z)^2}) \sin^2 \gamma,$

где $q^x = \frac{q^1}{\vert \dot {\mathbf q} \vert}$ , $q^y = \frac{q^2}{\vert \dot {\mathbf q} \vert}$ , $q^z = \frac{q^3}{\vert \dot {\mathbf q} \vert}$ , то кватернион $\dot q$ запишется так:

$\dot q = \cos \gamma + \dot {\mathbf q}_n \sin \gamma,$

где $\dot {\mathbf q}_n = iq^x + jq^y + kq^z$ . Если теперь взять произвольный кватернион $\dot R$ с нулевой скалярной частью и вектором $\dot {\mathbf R}$ , то результатом операции

$\dot R^{'} = \dot q \circ \dot R \circ \dot q^{-1} \qquad (5)$

будет вектор $\dot{\mathbf R}^{'}$ с той же длиной, что и $\dot {\mathbf R}$ , но повёрнутый на угол $2 \gamma$ против часовой стрелки вокруг оси, направляющим вектором которой является $\dot {\mathbf q}_n$ . Дальше будут встречаться фразы вроде "кватернион $\dot q$ выполняет поворот вектора $\dot R$ ", которые, конечно, подразумевают применение кватерниона $\dot q$ к вектору $\dot{\mathbf R}$ и получение $\dot{\mathbf R}^{'}$ в соответствии с (5).

Последний теоретический момент. Для обозначения разных видов умножения используются такие общеизвестные значки: $\dot {\mathbf q} \dot {\mathbf r}$ или $\dot {\mathbf q} \cdot \dot {\mathbf r}$ : скалярное произведение, $\dot q \circ \dot r$ : кватернионное произведение, $\dot {\mathbf q} \times \dot {\mathbf r}$ : векторное произведение.

На этом с теорией всё.

Описание решения с кватернионами

Вернёмся к векторам $\mathbf R_{ki}^{'}$ и $\mathbf R_{ki}$ . Три замечания об их характере, которые потребуются дальше. Примем пока k = 1 , i = 2.

Нужные замечания

Во-первых, эти векторы являются свободными векторами, которые можно перемещать в пространстве, соблюдая параллельность перемещений.

Во-вторых, они неколлинеарны. Действительно, если бы они были коллинеарными, то (3) обращалось бы в истинное высказывание только при единичной матрице $\mathbf M$ и задачу решать не нужно было.

И, в-третьих, $\vert \mathbf R_{12}^{'} \vert = \vert \mathbf R_{12} \vert$ . В самом деле, так как $\mathbf M$ - это ортогональная матрица, которая не меняет длину вектора $\mathbf R_{12}^{'}$ , то из (3) следует, что длины векторов $\mathbf R_{12}^{'}$ и $\mathbf R_{12}$ равны.

Tак как в (3) длины векторов не имеют значения, для упрощения записей и решения дальше заменю векторы $\mathbf R_{12}^{'}$ и $\mathbf R_{12}$ их нормированными эквивалентами:

$\mathbf r_1 \equiv \frac{\mathbf R_{12}}{\vert \mathbf R_{12} \vert} = \begin{bmatrix} r_1^1 & r_1^2 & r_1^3 \end{bmatrix}^T, \qquad \mathbf p_1 \equiv \frac{\mathbf R_{12}^{'}}{\vert \mathbf R_{12}^{'} \vert} = \begin{bmatrix} p_1^1 & p_1^2 & p_1^3 \end{bmatrix}^T,$

и в виде кватернионов:

$\dot r = 0 + \mathbf{\dot r}_1 = 0 + ir_1^1 + jr_1^2 + kr_1^3, \quad \dot p = 0 + \mathbf{\dot p}_1 = 0 + ip_1^1 + jp_1^2 + kp_1^3.$

Кватернионная форма основных уравнений

Выражение (3) в кватернионной форме выглядит теперь так:

$\dot q \circ \dot r_1 \circ \dot q^{-1} = \dot p_1,\qquad (6)$

где $\dot q$ - неизвестный кватернион, эквивалент $\mathbf M$ , а выражение (1) так:

$\dot R_a = \dot R_1 - \dot q \circ \dot R_1 \circ \dot q^{-1}, \qquad (7)$

где $\dot R_a = 0 + ix_a + jy_a + kz_a$ , $\dot R_1 = 0 + ix_1 + jy_1 + kz_1$ .

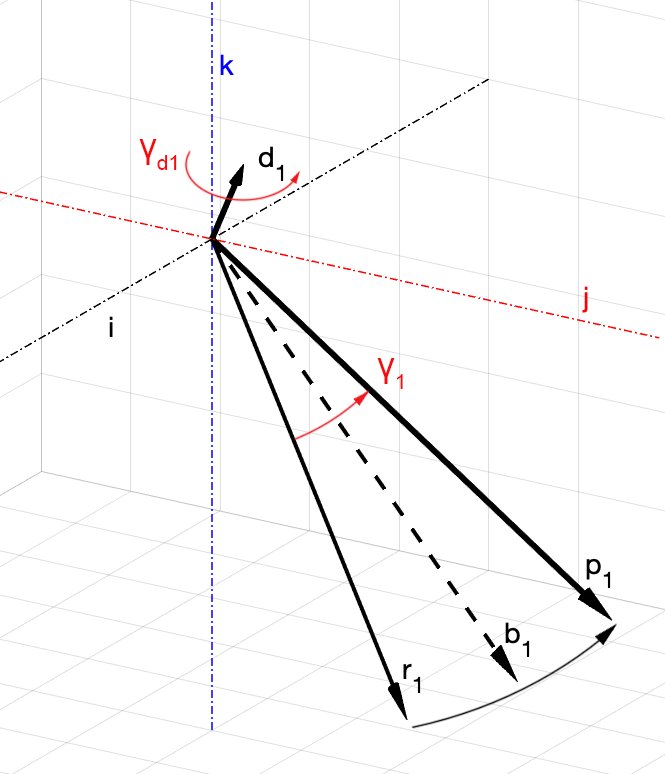
Так как векторы $\dot {\mathbf r}_1$ и $\dot {\mathbf p}_1$ свободны, неколлинеарны, то можно совместить их концы таким образом, чтобы $\dot {\mathbf r}_1$ и $\dot {\mathbf p}_1$ образовали угол $\gamma_1$ на плоскости, натянутой на эти векторы (пусть эта плоскость будет $\lambda_1$ ). Начало координат поместим в точку, общую для $\dot {\mathbf r}_1$ и $\dot {\mathbf p}_1$ (рис. 3), и будем полагать, что значение $\gamma_1$ известно.

Уравнение (6), аналогично уравнению (3), по-прежнему имеет бесконечное множество решений: можно найти сколько угодно различных $\dot q$ , которые удовлетворяют (6). Геометрически это обозначает, что можно найти бесконечное число различных прямых, вокруг которых можно выполнить вращение, совмещающее $\dot {\mathbf r}_1$ с $\dot {\mathbf p}_1$ . На рис. 3 приведён пример, в котором поворот выполняется по кратчайшему пути вокруг прямой с направляющим вектором $\dot {\mathbf d}_1$ , ортогональным плоскости $\lambda_1$ . Очевидно, что $\gamma_{d_1}\ = \gamma_1$ .

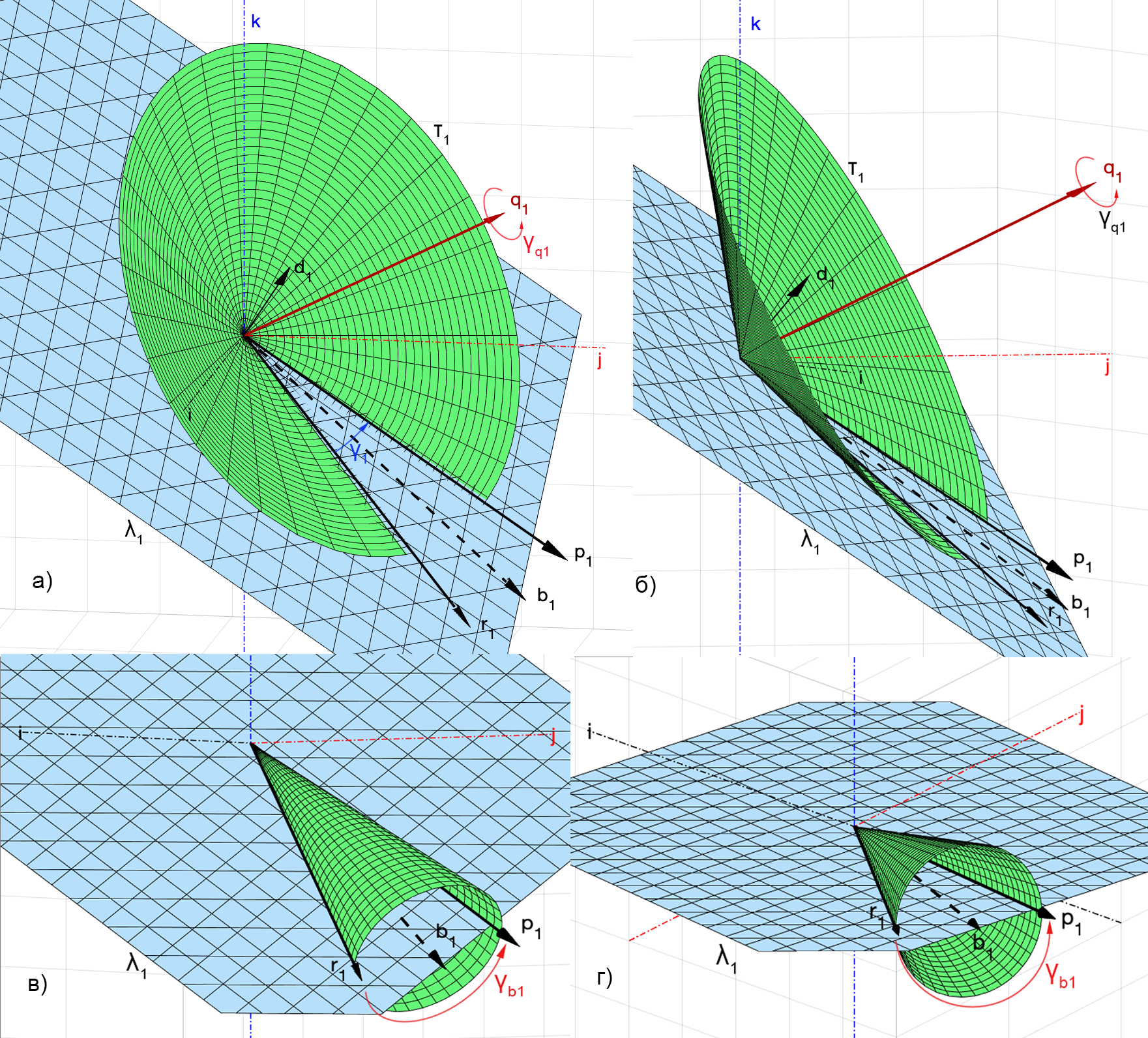
На рис. 4, а) и б) приведён пример, в котором вокруг некоторой оси с направляющим вектором $\dot {\mathbf q}_1$ построен круговой конус $\tau_1$ с направляющими прямыми $\dot {\mathbf r}_1$ и $\dot {\mathbf p}_1$ . Ясно, что вокруг такой оси можно сделать поворот, совмещающий $\dot {\mathbf r}_1$ с $\dot {\mathbf p}_1$ , который будет выполнен не по кратчайшему пути (не в плоскости $\lambda_1$ ), и угол $\gamma_{q_1}$ , измеряемый в плоскости основания конуса $\tau_1$ , не будет равен $\gamma_1$ , измеряемый в плоскости $\lambda_1$ .

Рис. 4. Поворот r к p вокруг произвольной оси

Чтобы найти неизвестное значение $\dot q$ , я добавил два новых объекта $\dot r_2 = \dot{R}_3^{'} - \dot{R}_1^{'}$ и $\dot p_2 = \dot R_3 - \dot R_1$ , получаемые из векторов $\mathbf R_3$ и $\mathbf R_1$ . Выражение (6), аналогично (4), расширяется до системы уравнений

$\begin{cases} \dot q \circ \dot r_1 \circ \dot q^{-1} = \dot p_1,\\ \dot q \circ \dot r_2\circ \dot q^{-1} = \dot p_2. \end{cases} \qquad (8)$

Теперь можно утверждать, что кватернион $\dot q$ , найденный из этой системы уравнений (8), является единственным решением, и он выполняет такой поворот в пространстве, который совмещает тройку векторов базиса ЛСК с векторами ГСК. Следовательно, его можно подставить в выражение (7) и вычислить искомое R_a - положение ОНВ.

Когда я записал (8), отчего-то стало ясно, что здесь безразмерная куча тригонометрии может не возникнуть, и аналитическое решение поэтому можно будет найти более-менее просто.

Геометрия задачи

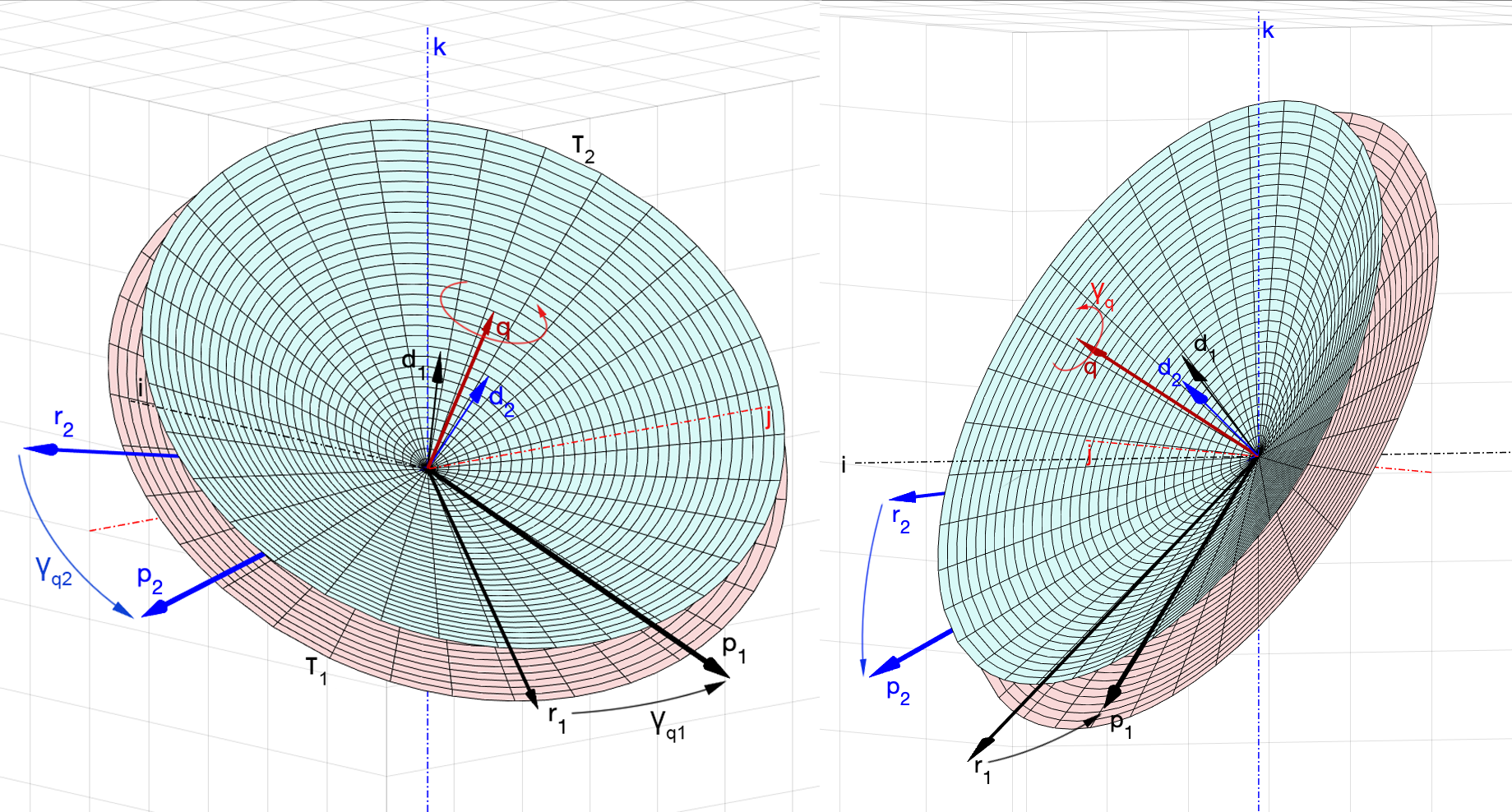
Геометрически задача теперь выглядит так. Нужно найти в пространстве такую ось, вокруг которой можно выполнить поворот, совмещающий вектор $\dot {\mathbf r}_1$ с вектором $\dot {\mathbf p}_1$ , и вектор $\dot {\mathbf r}_2$ с вектором $\dot {\mathbf p}_2$ . Прямые, направляющими векторами которых являются $\dot {\mathbf r}_1$ (или $\dot {\mathbf p}_1$ ) и $\dot {\mathbf r}_2$ (или $\dot {\mathbf p}_2$ ), образуют два различных круговых конуса $\tau_1$ , $\tau_2$ . Эти конусы имеют общую ось, направляющим вектором которой является искомый $\dot {\mathbf q}$ . При этом повороты $\dot {\mathbf r}_i$ к $\dot {\mathbf p}_i$ , i = 1, 2, будут выполняться не по кратчайшему пути, и поэтому углы $\gamma_{q_i}$ , измеренные в плоскости оснований конусов $\tau_i$ , будут отличаться от углов $\gamma_i$ (рис. 5).

Здесь и далее нам понадобятся два таких утверждения.

Утверждение 1. Угол поворота вокруг биссектрисы $\dot {\mathbf b}_1$ такого, который совмещает $\dot {\mathbf r}_1$ с $\dot {\mathbf p}_1$ , равен $\pi$ (рис. 4, в), г)).

Утверждение 2. Поворот, который совмещает $\dot {\mathbf r}_i$ с $\dot {\mathbf p}_i$ , i = 1, 2, вокруг некоторой прямой можно сделать тогда и только тогда, когда эта прямая лежит в плоскости, натянутой на $\dot {\mathbf d}_i$ и $\dot {\mathbf b}_i$ (плоскость $\delta_i$ ), рис. 6). Вокруг любой другой прямой такой поворот выполнить нельзя.

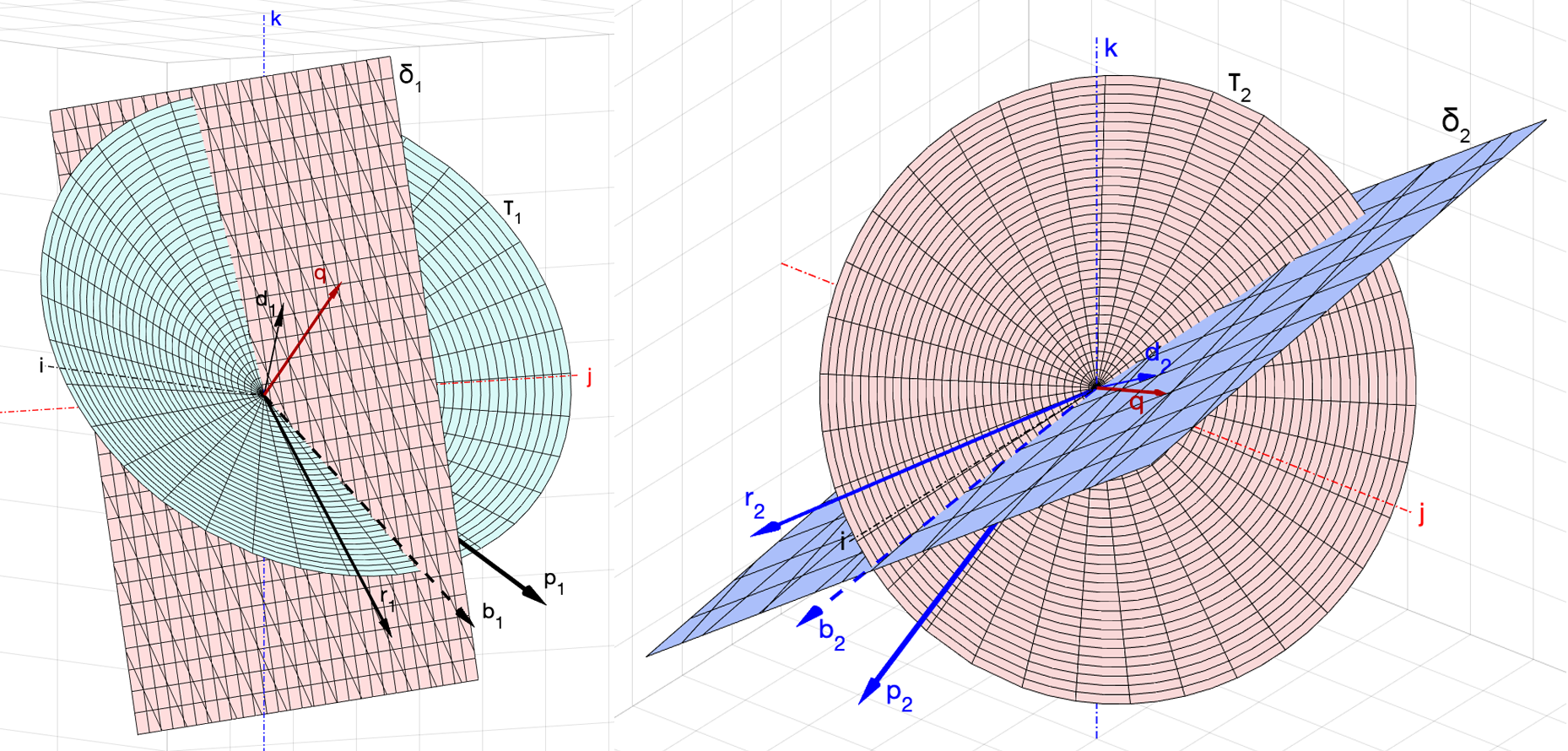
Для доказательства этих утверждений нужно рассмотреть свойства кругового конуса $\tau_i$ , образованного линией, направляющий вектор которой равен $\dot {\mathbf r}_i$ (или $\dot {\mathbf p}_i$ ), а ось лежит в плоскости $\delta_i$ .

Очевидно, что ось, вокруг которой можно сделать такой поворот, который совместит $\dot {\mathbf r}_i$ с $\dot {\mathbf p}_i$ , i = 1, 2, будет одновременно принадлежать обеим плоскостям $\delta_i$ , то есть будет совпадать с линией их пересечения. Поэтому вектор $\dot {\mathbf q}$ будем искать из уравнения линии пересечения плоскостей $\delta_i$ (рис. 7).

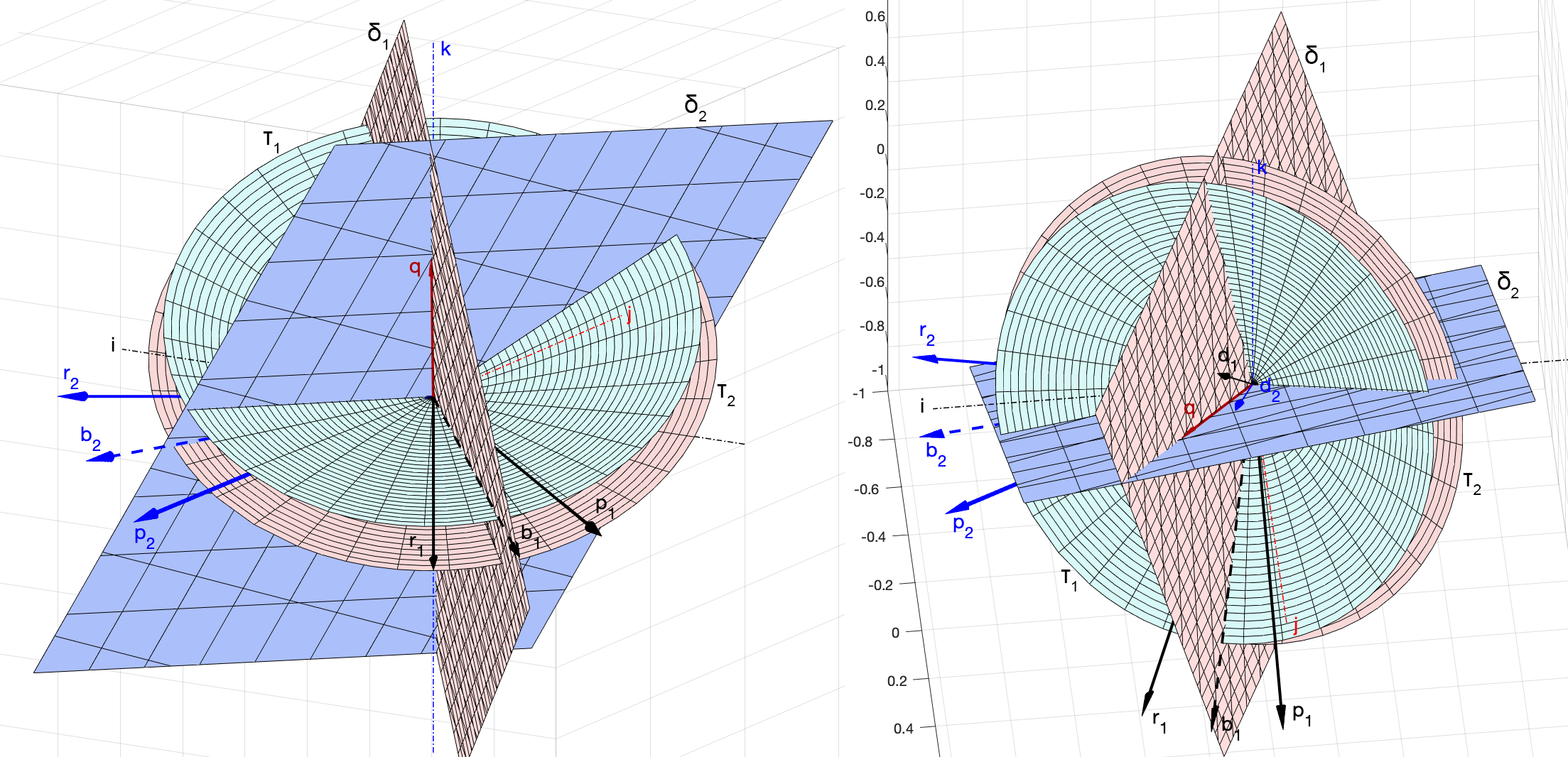
Эта прямая не будет совпадать с прямыми, определяемые направляющими векторами $\dot {\mathbf d}_i$ . Проходя через начало координат, она образует некоторый угол $\beta_1$ с вектором $\dot {\mathbf d}_1$ , и угол $\beta_2$ с вектором $\dot {\mathbf d}_2$ (рис. 8). Оба этих угла нам пока неизвестны и $\beta_1 \ne \beta_2$ .

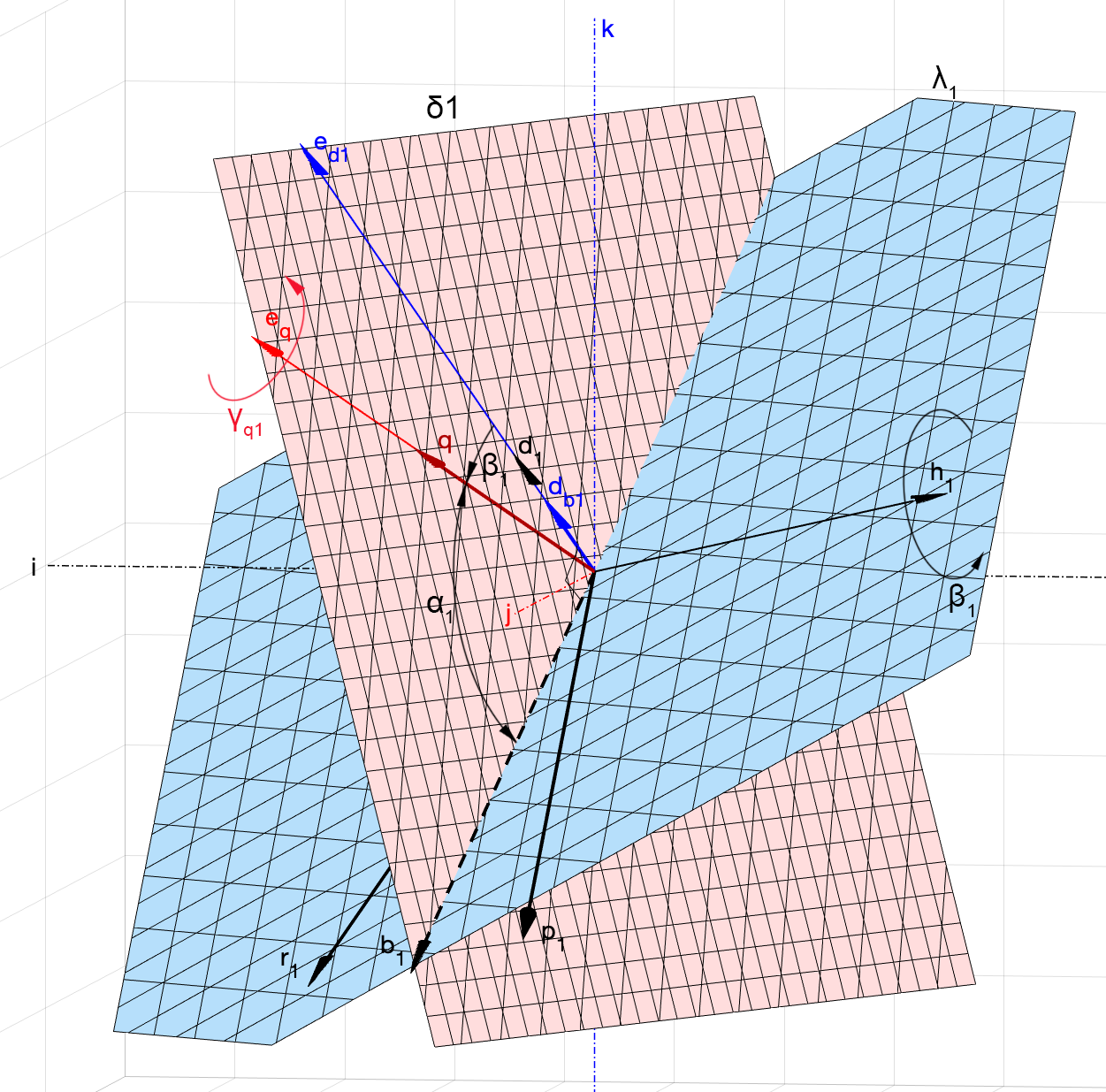
Посмотрим на рис. 8. Если взять некоторый кватернион $\dot e_{d_1}$ , который поворачивает вектор $\dot {\mathbf r}_1$ на $\pi$ в плоскости $\lambda_1$ , т.е.

$\dot e_{d_1} = 0 + \dot {\mathbf s}_1, \qquad (9)$

и повернуть его вокруг начала координат на угол $\beta_1$ в плоскости $\delta_1$ , то из

$\dot e_{q_1}(\beta_i) = \dot h_1(\beta_1) \circ \dot e_{d_1} \circ \dot h_1^{-1}(\beta_1) \qquad (10)$

мы получим вектор $\dot {\mathbf e}_{q_1}(\beta_1)$ , который в свою очередь является кватернионом поворота на угол $\pi$ для вектора $\dot {\mathbf r}_1$ , причём $\dot {\mathbf r}_1$ при этом будет описывать дугу в пространстве. Поворот $\dot {\mathbf e}_{d_1}$ к $\dot {\mathbf e}_{q_1}$ может быть выполнен кватернионом $\dot h_1(\beta_1)$ , который мы найдём чуть позже из условия его ортогональности к плоскости $\delta_1$ .

Из утверждения 2 следует, что вектор $\dot {\mathbf r}_1$ может быть совмещён с $\dot {\mathbf p}_1$ вращением вокруг оси с направляющим вектором $\dot {\mathbf e}_{q_1}(\beta_1)$ на некоторый угол $\gamma_{q_1}$ , который, очевидно, функционально зависит от $\beta_1$ . Поэтому, зная $\beta_1$ и зависимость $\gamma_{q_1} = f(\beta_1)$ , мы сможем построить из кватерниона $\dot {\mathbf e}_{q_i}$ кватернион $\dot q$ , являющийся решением задачи.

Зависимость $\gamma_{q_1} = f(\beta_1)$ мы найдём немного позже из простых тригонометрических соотношений.

Угол $\beta_1$ будем искать из следующих соображений. Так как $\dot {\mathbf q}$ ортогонален одновременно $\dot {\mathbf h}_1$ и $\dot {\mathbf h}_2$ , то результат векторного произведения $\dot {\mathbf h}_1(\beta_1) \times \dot {\mathbf h}_2(\beta_2)$ будет сонаправлен с $\dot {\mathbf q}$ . Обозначим

$\dot {\mathbf q}_e \equiv \dot {\mathbf h}_1(\beta_1) \times \dot {\mathbf h}_2(\beta_2) \qquad (11)$

и запишем такое скалярное произведение: $\dot {\mathbf e}_{q_1}(\beta_1) \dot {\mathbf q}_e$ . Отметим, что направление $\dot {\mathbf q}_e$ не зависит ни от $\beta_1$ , ни от $\beta_2$ . Поэтому для вычисления $\dot {\mathbf q}_e$ примем $\dot h_1 = \dot h_1 (\beta_1) \vert _{\beta_1 = \pi}$ и $\dot h_2 = \dot h_2 (\beta_2) \vert _{\beta_2 = \pi}$ , то есть угол, при котором $\vert \dot {\mathbf h}_i \vert = 1$ . Следовательно, в записанном выше скалярном произведении остаётся одна переменная $\beta_1$ , которую можно вычислить, решив уравнение

$\dot {\mathbf e}_{q_1}(\beta_1) \frac{\dot {\mathbf q}_e}{ \vert \dot {\mathbf q}_e \vert } = \dot {\mathbf e}_{q_1}(\beta_1) \dot{\mathbf q}_{e_{n}} = 1, \qquad (12)$

полагая, что $\vert \dot {\mathbf e}_{q_1} (\beta_1) \vert = 1$ . Теперь, зная $\beta_1$ , зависимость $\gamma_{q_1} = f(\beta_1)$ и вектор $\dot {\mathbf e}_{q_1}(\beta_1)$ , искомый кватернион $\dot {\mathbf q}$ будет выглядеть так:

$\dot {\mathbf q} = \cos \frac{\gamma_{q_1}}{2} + \dot {\mathbf e}_{q_1} \sin \frac{\gamma_{q_1}}{2}. \qquad (13)$

Осталось найти каждый из описанных выше элементов, чтобы решить задачу. Заметим, что объекты $\dot e_{d_2 }$ , $\dot e_{q_2}$ , $\dot h_2$ , $\beta_2$ , $\gamma_2$ , $\gamma_{q_2}$ определяются аналогично. Поэтому далее нижний индекс "1" или "2" буду заменять на " i ", подразумевая, что i = 1, 2 .

Кватернионы, которые будем искать

Ещё раз перечислим кватернионы и векторы, которые мы сейчас будем строить для получения решения:

кватернион $\dot d_i$ : совмещает вектор $\dot{\mathbf r}_i$ с $\dot{\mathbf p}_i$ по кратчайшей траектории,
кватернион $\dot b_i$ : направляющий вектор биссектрисы угла между векторами $\dot{\mathbf r}_i$ и $\dot{\mathbf p}_i$ ; векторы $\dot{\mathbf d}_i$ и $\dot{\mathbf b}_i$ определяют плоскость $\delta_i$ , в которой лежит искомый кватернион $\dot q$ ,
кватернион $\dot e_{d_i}$ : сонаправлен с $\dot d_i$ ; модуль векторной части $\dot e_{d_i}$ равен 1,
кватернион $\dot h_i(\beta_i)$ : поворачивает вектор $\dot{\mathbf e}_{d_i}$ в плоскости $\delta_i$ на угол $\beta_i$ ; значение $\beta_i$ неизвестно,
зависимость $\gamma_{q_i} = f(\beta_i)$ : вычисляет $\gamma_{q_i}$ для построения искомого кватерниона $\dot q$ из $\dot e_{q_i}$ ,
кватернион $\dot e_{q_i} (\beta_i)$ : получен поворотом вектора $\dot{\mathbf e}_{d_i}$ в плоскости $\delta_i$ на угол $\beta_i$ ; из $\dot e_{q_i}$ будет получено решение,
кватернион $\dot q_e$ : нужен для вычисления угла $\beta_i$ ,
и, наконец, результирующий кватернион $\dot q$ : получается из $\dot e_{q_i}$ , учитывая найденные $\beta_i$ и $\gamma_{q_i}$ .

Кватернион $\dot d_i$

Найдём кватернион $\dot d_i$ , который совмещает $\dot {\mathbf r}_i$ с $\dot {\mathbf p}_i$ по кратчайшей траектории. Вектор $\dot {\mathbf r}_i$ перемещается в плоскости $\lambda_i$ , а ось поворота перпендикулярна $\lambda_i$ и проходит через точку начала координат (рис. 3). Направляющий вектор этой оси может быть равен $\dot { \mathbf r}_i \times \dot {\mathbf p}_i$ . Так как $\vert \dot {\mathbf r}_i \vert = \vert \dot {\mathbf p}_i \vert = 1$ , и $\vert \dot {\mathbf r}_i \times \dot {\mathbf p}_i \vert = \vert \dot {\mathbf r}_i \vert \vert \dot {\mathbf p}_i \vert \sin \gamma_i$ , то:

$\dot {\mathbf r}_i \times \dot {\mathbf p}_i = \frac{ \dot {\mathbf r}_i \times \dot {\mathbf p}_i }{ \vert \dot {\mathbf r}_i \times \dot {\mathbf p}_i \vert } \vert \dot {\mathbf r}_i \times \dot {\mathbf p}_i \vert = \dot {\mathbf s}_i \sin \gamma_i, \qquad (14)$

где $\dot {\mathbf s}_i$ - единичный вектор, равный

$\dot {\mathbf s}_i = \frac{1}{\sin \gamma_i} \begin{vmatrix} i & j & k \\ r_i^1 & r_i^2 & r_i^3 \\ p_i^1 & p_i^2 & p_i^3 \end{vmatrix} = is_i^x + js_i^y + ks_i^z, \qquad (15)$

где

$s_i^x = \frac{r_i^2 p_i^3 - r_i^3 p_i^2}{\sin \gamma_i}, \quad s_i^y = \frac{r_i^3 p_i^1 - r_i^1 p_i^3}{\sin \gamma_i}, \quad s_i^z = \frac{r_1^1 p_1^2 - r_i^2 p_i^1}{\sin \gamma_i}. \qquad (16)$

Произведение $\dot {\mathbf s}_i \sin \gamma_i$ может представлять собой векторную часть некоторого кватерниона $\dot s_i$ , который выполняет поворот вектора $\dot {\mathbf r}_i$ на угол $2 \gamma_i$ в плоскости $\lambda_i$ : $\dot s_1 = \cos \gamma_i + \dot {\mathbf s}_i \sin \gamma_i$ . Поэтому кватернион поворота $\dot {\mathbf d}_i$ на угол $\gamma_i$ равен

$\dot d_i = \cos \frac{\gamma_i}{2} + \dot {\mathbf s}_i \sin \frac{\gamma_i}{2} \qquad (17)$

$\dot p_i = \dot d_i \circ \dot r_i \circ \dot d_i^{-1}.$

Кватернион $\dot b_i$

Найдём кватернион $\dot b_i$ . Он может быть получен из преобразования

$\dot b_i = \dot d_{b_i} \circ \dot r_i \circ \dot d_{b_i}^{-1}, \qquad (18)$

где $\dot d_{b_i}$ - кватернион, выполняющий поворот вектора $\dot {\mathbf r}_i$ на угол $\frac{\gamma_i}{2}$ . Учитывая (17), он равен

$\dot d_{b_i} = \cos \frac{\gamma_i}{4} + \dot {\mathbf s}_1 \sin \frac{\gamma_a}{4}. \qquad (19)$

Подставим $\dot d_{b_i}$ из (19) в (18), выполним кватернионные умножения и, учитывая (14), получим:

$\begin{split} \dot b_i = \dot {\mathbf r}_i \cos^2 \frac{\gamma_i}{4} - \dot {\mathbf r}_i \circ \dot {\mathbf s}_i \sin \frac{\gamma_i}{4} \cos \frac{\gamma_i}{4} + \dot {\mathbf s}_i \circ \dot {\mathbf r}_i \sin \frac{\gamma_i}{4} \cos \frac{\gamma_i}{4} - \dot {\mathbf s}_i \circ \dot {\mathbf r}_i \circ \dot {\mathbf s}_i \sin^2 \frac{\gamma_i}{4} = \\ = \dot {\mathbf r}_i \cos^2 \frac{\gamma_i}{4} - \dot {\mathbf r}_i \times (\dot {\mathbf r}_i \times \dot {\mathbf p}_i) \frac{\sin \frac{\gamma_i}{2}}{\sin \gamma_i} - ((\dot {\mathbf r}_i \times \dot {\mathbf p}_i) \times \dot {\mathbf r}_i ) \times (\dot {\mathbf r}_i \times \dot {\mathbf p}_i ) \frac{\sin^2 \frac{\gamma_i}{4}}{\sin^2 \gamma_i}. \end{split}$

Применяя правило "БАЦ минус ЦАБ" и упрощая, получаем

$\dot b_i =0 + (\dot {\mathbf r}_i + \dot {\mathbf p}_i) \frac{\sin \frac{\gamma_i}{2}}{\sin \gamma_i}. \qquad (20)$

Заметим, что $\vert \dot {\mathbf b}_i \vert = 1$ .

Зависимость $\gamma_{q_1} = f(\beta_1)$

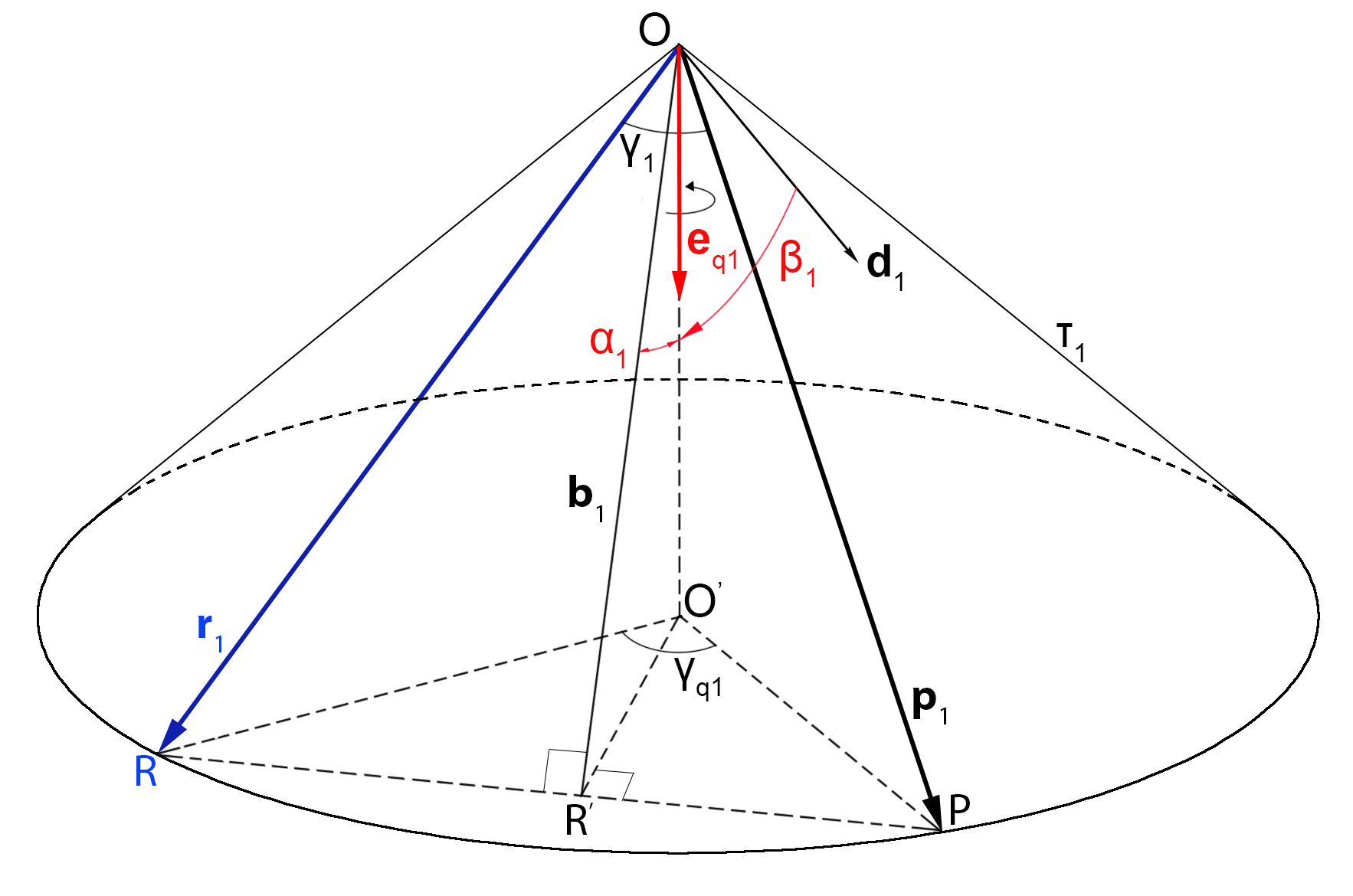
Найдём зависимость $\gamma_{q_1} = f(\beta_1)$ . Возьмём конус $\tau_1$ из рис. 6, для удобства развернём его основанием вниз и изобразим все основные векторы и углы (рис. 9). Также добавим угол $\alpha_i = \frac{\pi}{2} - \beta_1$ .

Будем находить зависимость угла $\gamma_{q_1}$ , соответствующего углу поворота вокруг $\dot {\mathbf q}_{e_1}$ от $\dot {\mathbf r}_1$ к $\dot {\mathbf p}_1$ , от значения угла $\beta_1$ , то есть от угла наклона $\dot {\mathbf q}_{e_1}$ к плоскости векторов $\dot {\mathbf r}_1$ , $\dot {\mathbf p}_1$ (т.е. к плоскости $\lambda_1$ ). Заметим, что при $\beta_1 = 0$ поворот выполняется по кратчайшей траектории вокруг $\mathbf{\dot d}_1$ .

Из соотношений прямоугольных треугольников запишем:

$\begin{split} \vert RR^{'} \vert = \vert \dot {\mathbf r} \vert \sin \frac{\gamma_1}{2}, \quad \vert \dot {\mathbf b}_1 \vert = \vert \dot {\mathbf r} \vert \cos \frac{\gamma_i}{2}, \quad \vert R^{'}O^{'} \vert = \vert \dot {\mathbf b}_1 \vert \sin \alpha_1, \end{split}$

откуда $\vert R^{'}O^{'} \vert = \vert \dot {\mathbf r}_1 \vert \cos \frac{\gamma_1}{2} \sin \alpha_1$ . Так как $\tan \frac{\gamma_{q_1}}{2} = \frac{\vert RR^{'} \vert }{\vert R^{'}O^{'} \vert}$ ), то

$\tan \frac{\gamma_{q_1} }{2} = \vert \dot {\mathbf r}_1 \vert \sin \frac{\gamma_1}{2} \frac{1}{\cos \frac{\gamma_1}{2} \sin \alpha_1} = \frac{1}{\sin \alpha_1} \tan \frac{\gamma_i}{2},$

откуда

$\gamma_{q_1} = 2 \arctan (\frac{1}{\cos \beta_1} \tan \frac{\gamma_1}{2}). \qquad (21)$

Из выражения (21) видно, что при $\beta_1 = 0$ значение $\gamma_{q_1} = \gamma_1$ , а при $\beta_1 = \frac{\pi}{2}$ значение $\gamma_{q_1} = \pi$ , что согласуется с утверждением 1. Заметим также, что угол $\gamma_{q_1}$ не зависит от длин векторов, а угол $\gamma_i$ полагается известным.

Кватернион $\dot h_i(\beta_i)$

Продолжим. Построим кватернион $\dot h_i$ . Поскольку он выполняет поворот $\dot{\mathbf e}_{d_i}$ на угол $\beta_i$ в плоскости $\delta_i$ , то

$\dot h_i(\beta_i) = \cos \frac{\beta_i}{2} + \dot{\mathbf e}_{d_i} \times \dot{\mathbf b}_i \sin \frac{\beta_i}{2}, \qquad (22)$

полагая, что $\vert \dot{\mathbf e}_{d_i} \vert = 1$ , $\vert \dot{\mathbf b}_i \vert = 1$ . Учитывая (9), (18), выполнив некоторые преобразования, получим

$\begin{split} \dot{\mathbf e}_{d_i} \times \dot{\mathbf b}_i = \dot{\mathbf r}_i (\tan^{-2} \gamma_i \sin \frac{\gamma_i}{2} - \tan^{-1} \gamma_i \cos \frac{\gamma_i}{2} - \frac{\sin \frac{\gamma_i}{2}}{\sin^2 \gamma_i}) + \dot{\mathbf p}_i (\frac{\cos \frac{\gamma_i}{2}}{\sin \gamma_i} - \frac{\cos \gamma_i}{\sin^2 \gamma_i} \sin \frac{\gamma_i}{2} + \frac{\sin \frac{\gamma_i}{2}}{\sin^2 \gamma_i}). \end{split}$

После упрощающих тригонометрических преобразований, подставляя в (22), получаем

$\dot h_i(\beta_i) = \cos \frac{\beta_i}{2} + (\dot{\mathbf p}_i - \dot{\mathbf r}_i) \frac{\cos \frac{\gamma_i}{2}}{\sin \gamma_i} \sin \frac{\beta_i}{2}, \qquad (23)$

при этом $\vert \dot h_i(\beta_i) \vert = 1$ .

Кватернион $\dot e_{q_i}(\beta_i)$

Найдём кватернион $\dot e_{q_i}$ . Выше мы записали выражение (9), которое определяет $\dot e_{q_i}$ . Приведём его здесь ещё раз: $\dot e_{q_i}(\beta_i) = \dot h_i(\beta_i) \circ \dot e_{d_i} \circ \dot h_i^{-1}(\beta_i)$ . Подставляя сюда полученный результат (23) и выражение (9), после преобразований получим:

$\dot e_{q_i} = C(A^2 \dot{\mathbf r}_i \times \dot{\mathbf p}_i -2AB(\dot{\mathbf r}_i + \dot{\mathbf p}_i)(\cos \gamma_i -1) - 2B^2 \dot{\mathbf r}_i \times \dot{\mathbf p}_i (1-\cos \gamma_i)),$

где $A \equiv \cos \frac{\beta_i}{2}$ , $B \equiv \frac{\cos \frac{\gamma_i}{2}}{\sin \gamma_i } \sin \frac{\beta_i}{2}$ , $C \equiv \frac{1}{\sin \frac{\gamma_i}{2}}$ . Упрощая, получаем:

$\dot e_{q_i} = \frac{1}{\sin \gamma_i} (\dot{\mathbf r}_i \times \dot{\mathbf p}_i \cos \beta_i + (\dot{\mathbf r}_i + \dot{\mathbf p}_i) \sin \frac{\gamma_i}{2} \sin \beta_i), \qquad (24)$

при этом $\vert \dot e_{q_i} \vert = 1$ .

Кватернион $\dot q_e$

Получим кватернион $\dot q_e$ . Как мы указывали выше, вектор этого кватерниона ортогонален каждому из векторов $\dot{\mathbf h}_1$ и $\dot{\mathbf h}_2$ , то есть $\dot {\mathbf q}_e \equiv \dot {\mathbf h}_i(\beta_i) \times \dot {\mathbf h}_i(\beta_i)$ (выражение (11)), и при этом $\vert \dot{\mathbf q}_e \vert \ne 1$ . Также мы отмечали, что угол $\beta_i$ не меняет направление вектора $\dot{\mathbf h}_i$ , и поэтому можно выбрать такое $\beta_i$ , при котором длина $\dot{\mathbf h}_i$ максимальна. Учитывая (23) при $\beta_i = \pi$ , получаем:

$\dot h_1 = (\dot{\mathbf p}_1 - \dot{\mathbf r}_1) \frac{\cos \frac{\gamma_1}{2}}{\sin \gamma_1}, \quad \dot h_2 = (\dot{\mathbf p}_2 - \dot{\mathbf r}_2) \frac{\cos \frac{\gamma_2}{2}}{\sin \gamma_2}, \qquad (25)$

следовательно,

$\dot{\mathbf q}_e = (\dot{\mathbf p}_1 - \dot{\mathbf r}_1) \times (\dot{\mathbf p}_2 - \dot{\mathbf r}_2) \frac{\cos \frac{\gamma_1}{2}}{\sin \gamma_1} \frac{\cos \frac{\gamma_2}{2}}{\sin \gamma_2}. \qquad (26)$

Нормированное значение

$\dot{\mathbf q}_{e_n} = \frac{ (\dot{\mathbf p}_1 - \dot{\mathbf r}_1) \times (\dot{\mathbf p}_2 - \dot{\mathbf r}_2) }{\vert (\dot{\mathbf p}_1 - \dot{\mathbf r}_1) \times (\dot{\mathbf p}_2 - \dot{\mathbf r}_2) \vert}. \qquad (27)$

Угол $\beta_i$

Подставляем результаты в выражение (12) и получаем уравнение, которое нужно решить относительно $\beta_1$ :

$\frac{1}{\sin \gamma_1} (\dot{\mathbf r}_1 \times \dot{\mathbf p}_1 \cos \beta_1 + (\dot{\mathbf r}_1 + \dot{\mathbf p}_1) \sin \frac{\gamma_1}{2} \sin \beta_1) \frac{ (\dot{\mathbf p}_1 - \dot{\mathbf r}_1) \times (\dot{\mathbf p}_2 - \dot{\mathbf r}_2) }{\vert (\dot{\mathbf p}_1 - \dot{\mathbf r}_1) \times (\dot{\mathbf p}_2 - \dot{\mathbf r}_2) \vert} = 1. \qquad (28)$

После преобразований получаем это уравнение в форме $A \cos \beta_1 + B \sin \beta_1 = 1$ , которое и решаем:

$\beta_1 = \arcsin \frac{1}{\sqrt{A^2 + B^2}} - \arcsin \frac{A}{\sqrt{A^2 + B^2}}, \qquad (29)$

где

$\begin{split} A = \frac{\dot{\mathbf r}_1 \times \dot{\mathbf p}_1}{\sin \gamma_1} \frac{ (\dot{\mathbf p}_1 - \dot{\mathbf r}_1) \times (\dot{\mathbf p}_2 - \dot{\mathbf r}_2) }{\vert (\dot{\mathbf p}_1 - \dot{\mathbf r}_1) \times (\dot{\mathbf p}_2 - \dot{\mathbf r}_2) \vert}, \quad B = \frac{\sin \frac{\gamma_1}{2}}{\sin \gamma_1} (\dot{\mathbf r}_1 + \dot{\mathbf p}_1) \frac{ (\dot{\mathbf p}_1 - \dot{\mathbf r}_1) \times (\dot{\mathbf p}_2 - \dot{\mathbf r}_2) }{\vert (\dot{\mathbf p}_1 - \dot{\mathbf r}_1) \times (\dot{\mathbf p}_2 - \dot{\mathbf r}_2) \vert} \end{split}.$

Решение

Зная $\beta_1$ , можно построить кватернион $\dot e_{q_1}$ из (24), подставить его в (13) и записать результат в виде:

$\dot q =\cos \frac{\gamma_{q_1}}{2} + \frac{1}{\sin \gamma_1} (\dot{\mathbf r}_1 \times \dot{\mathbf p}_1 \cos \beta_1 + (\dot{\mathbf r}_1 + \dot{\mathbf p}_1) \sin \frac{\gamma_1}{2} \sin \beta_1) \sin \frac{\gamma_{q_1}}{2}, \qquad (30)$

где

$\gamma_{q_1} = 2 \arctan (\frac{1}{\cos \beta_1} \tan \frac{\gamma_1}{2}), \qquad (31)$

а $\beta_1$ вычисляется из выражения (29).

Послесловие

Задача решена. Я попытался упростить итоговое выражение (30), но пока не получилось. В моделях оно работает, поэтому пока оставлю, как есть. На рис. 10 приведён простой пример нахождения ориентации ЛСК для того, чтобы затем определить R_a .

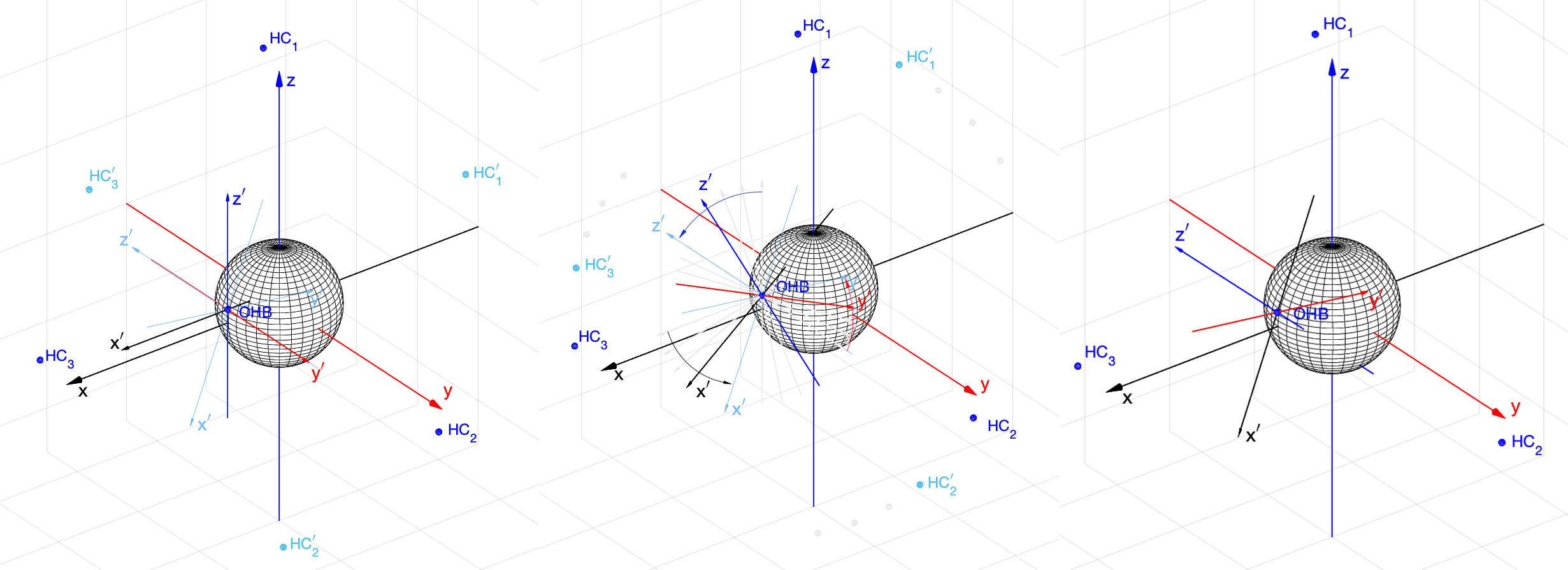
Вначале положение ЛСК $(x^{'}, y^{'}, z^{'})$ неизвестно, и мы полагаем, что оно может быть любым или, например, совпадающим с ГСК (то есть, мы "думаем", что оно совпадает, а на самом деле это не так). Измеренные координаты НС1', НС2' и НС3' существенно отличаются от истинных положений НС1, НС2 и НС3 (рис. 10, а)). Зная координаты НС в ГСК, вычисляется кватернион поворота $\dot q$ по (30) и выполняется вращение. На рис. 10, б) показано дискретное вращение с интервалом 10 градусов от старого положения ЛСК к истинному. При этом измеренные координаты НС (показаны светло-серым цветом) всё более приближаются к истинным. На рис. 10, в) показано вычисленное истинное положение ЛСК, и мы теперь можем определить R_a , то есть решить навигационную задачу (точнее, часть навигационной задачи, связанной с определением координат).

На этом пока всё. Отмечу только, что в ближайшем будущем я попробую поработать над одним недостатком выражения (30). При $\gamma_1$ близким к нулю, то есть когда ориентации ГСК и ЛСК мало отличаются, кватернион $\dot q$ вычисляется с ошибкой из-за множителя $\frac{1}{ \sin \gamma_1}$ . Это может приводить к значительным ошибкам вычисления ориентации ЛСК и, как результат, ошибкам определения положения R_a . Об этом в следующем материале.

Let's block ads! (Why?)

Парсер Хабра

...

суббота, 3 апреля 2021 г.

Кватернионы. Решение одной навигационной задачи

История

Входные данные

Задача

Решение

Неудачный поиск решения

Теория о кватернионе поворота

Описание решения с кватернионами

Нужные замечания

Кватернионная форма основных уравнений

Геометрия задачи

Кватернионы, которые будем искать

Послесловие

Комментариев нет:

Отправить комментарий

...

суббота, 3 апреля 2021 г.

Кватернионы. Решение одной навигационной задачи

История

Входные данные

Задача

Решение

Неудачный поиск решения

Теория о кватернионе поворота

Описание решения с кватернионами

Нужные замечания

Кватернионная форма основных уравнений

Геометрия задачи

Кватернионы, которые будем искать

Послесловие

Комментариев нет:

Отправить комментарий

суббота, 3 апреля 2021 г.