
От переводчика:
Представляю вашему вниманию статью авторства Andy Gainey, в прошлом независимого разработчика игровых инструментов, ныне сотрудника Paradox Development Studio. На мой взгляд, автор играючи создал один из лучших процедурных генераторов планет с открытым исходным кодом.
Дата публикации статьи: 2014/09/30

Последние две с половиной недели я работал над процедурным генератором планет. В эти выходные я наконец достаточно отшлифовал его, чтоб убедить себя выложить его в сеть. Можете посмотреть на него здесь. (Под капотом ресурсоемкий код на JavaScript, так что я рекомендую Chrome. Firefox и IE работают медленнее, но справляются. В других браузерах я пока не пробовал. И еще, я пока что не разбирался с тач-управлением, так что практически всё здесь работает только клавиатурно. Мобильные пользователи, извините). (Вверху находится ссылка на версию 2, загружена 7 апреля 2015, версия 1 всё еще доступна здесь).
Обновление, октябрь 2015: вдохновившись этим прототипом, был выпущен Worldbuilder версии 0.2.2. Включает в себя различные плоские проекции карты и детализацию вплоть до пикселя.
Генерация планеты включает в себя множество различных шагов, с применением разнообразных алгоритмов и техник. Они неидеальны, и некоторые из них, по-правде говоря, вычурны, и требуют тонкой настройки параметров и поведения. Некоторые из них плохи настолько, что мне от них не по себе. Но они работают. Работают достаточно неплохо для того, чтобы получать приятно выглядящие, и достаточно разнообразные планеты, так что эти механизмы вполне могут стать подспорьем при разработке механики какой-нибудь стратегической игры. Так что в случае, если кому-то удастся использовать некоторые полезные идеи из моей работы, дайте мне знать, что получилось (и сделайте побольше красочных картинок).
Статья длинная, так что вот содержание:
- Цилиндры и Сферы
- Тесселяция Сферы
- Иррегулярности Повсюду
- Подразделяемые Икосаэдры
- Возвышенности
- Погода
- Биомы
- Код, Библиотеки, и прочие мелочи
- Итог
Цилиндры и Cферы

До того как я углублюсь в технические подробности, пара слов о моей изначальной мотивации. Последние несколько лет у меня были некоторые расплывчатые идеи об игре, являющейся несоревновательной адаптацией Civilization, в жанре песочницы. И чтобы это было в масштабе целой планеты. Но меня всегда раздражало, что стандартные планетарные карты почти всегда оказывались цилиндрическими. Будь на ней квадратная, изометрическая, или гексагональная сетка, раз карта замыкается слева и справа, но не сверху и снизу, она фактически является цилиндрической.

Это эффективная и простая техника, создающая некоторое подобие планетарной карты. Но многое в ней будет недоступно. Проложение траекторий ракет и судоходных путей через полюса, например. Так же это приводит к странности, которую вполне можно игнорировать, когда расстояние вокруг земного шара одинаковое далеко на севере (или юге), и на экваторе. Такого конечно не может быть в мире, близком к сферическому.
Так что, из-за этого раздражения, и возможно еще ради того, чтобы попросту "принять вызов", я потратил некоторое время в размышлениях, как решить задачу получения более сферической карты. Но в тоже время, карты, поделенной на тайлы. Как в Civilization, и многих других стратегических играх, я хотел оставить тайловую систему. Довольно много других игр успешно экспериментировали со сферическими картами, построенными не на тайлах. Но лично я не знаю ничего о тех, где пытались сделать сферичность, оставляя при этом строгую тайловую систему для передвижений и других стратегических элементов. Мне нравятся механики тайловых карт, и я хочу привнести туда ощущения сфероидального мира.
Тесселяция Сферы
Я теперь легко понимаю, почему до сих пор не сталкивался с играми, в которых это пробовали сделать. Пытаться разместить тайлы на сфере это крайне тяжелое и неблагодарное дело. Максимальное число идеально однородных тайлов — 20, в виде треугольников, образующих икосаэдр. При любом превышении двадцатки необходимо уходить от однородности, и тут есть несколько путей. Это могут быть тайлы с разными количеством соседей, как в усечённом икосаэдере, гексагоны и пентагоны вперемешку. Или это могут быть тайлы полностью одинакового полигонального типа, но в различной степени искаженные, как если бы мы разделяли куб и затем проецировали все точки на сферу. У нас бы было много четырехугольников, но очень мало из них выглядело бы квадратными. Подход с разделением и проекцией также ведет предсказуемому появлению нескольких изолированных точек, с которыми соприкасается меньше тайлов, чем обычно. С разделяемым кубом, это происходит по крайней мере в восьми изначальных углах куба, где лишь три квадрата касаются точки вместо четырых. Или, в случае усеченного икосаэдра, где лишь пять треугольников касаются точек вместо шести (это можно увидеть на следующей внизу картинке, на многограннике справа сверху).
В целом, игра вполне может использовать технику подразделения, принимая некоторые нерегулярности, как компромисс. Любые стратегические эффекты, такие как редкие, но предсказуемо расположенные пентагонные тайлы, в которых проще держать оборону, так как их можно атаковать лишь с пяти сторон вместо шести — могут быть восприняты как особенности данной игровой механики. Однако я был слишком упрям, чтобы согласиться с этим. К счастью, мне уже довелось придумать творческое решение этой головоломки в прошлом году, и с тех пор оно находилось в моей голове.
Иррегулярности Повсюду
Проблема перемежающихся иррегулярностей состоит в их предсказуемости. Если их много, они образуют очень прослеживаемую и неорганичную структуру. Если их слишком мало, то благодаря изолированности, они выглядят "белыми воронами". Но что если бы они не были предсказуемы? Что если бы они не были изолированными?
Если бы иррегулярности могли потенциально находиться повсеместно, и притом слегка зависеть от расположения друг друга? Иногда располагаясь прямо вплотную друг к другу, или даже соединяясь в кластеры из трех-четырех штук? Может тогда они перестанут выглядеть неуместно. Может тогда они станут более естественной частью игровой механики, нежели чем простой девиацией.
Итак, как можно разбить сферу на тайлы органично? Вдохновившись отличной статьей от Amit Patel о генерации полигональных карт, вначале я попробовал сгенерировать набор случайных равномерно распределенных по поверхности сферы точек, а затем создать на их базе диаграмму Вороного. К сожалению, я несколько застрял на этом, так как большинство материалов по диаграмме Вороного фокусируется лишь на двумерных диаграммах. Найти доступные описания было непросто, и адаптировать всё это к трем измерением оказалось каверзной задачей. Всё усложнял тот факт, что я притом хочу получить двумерную диаграмму, но не в евклидовом пространстве, а в сферическом. Но меня вдохновил один двумерный метод, который я нашел. Основная идея в том, что вы берете 2D набор точек, и проецируете их на 3D параболу (попросту вычисляя z = x2 + y2). Затем вы находите выпуклую оболочку для 3D точек, которая, благодаря свойствам параболических проекций, гарантированно включает в себя все точки. Выпуклая оболочка будет удобным эквивалентом триангуляции Делоне для точек. А триангуляция Делоне как раз легко конвертируется в соответствующую диаграмму Вороного.
Как и в случае с параболой, я знал что все мои точки будут включены в выпуклую оболочку, так что чтобы получить диаграмму Вороного, мне оставалось лишь научиться построению выпуклой оболочки. Однако разобраться в том как эффективно её строить оказалось гораздо сложнее, чем я ожидал. Опять же, справочные материалы фокусировались работе с плоскостями. У меня получилось создать вроде бы рабочий рекурсивный "разделяй-и-властвуй" алгоритм, но он был уродлив. На каждом шагу был риск создать пару вогнутых треугольников, так что в алгоритме приходилось постоянно это проверять и чинить сетку треугольников каждый раз когда генерировалась такая вогнутость.
Когда всё это начало работать, я применил алгоритм Ллойда для релаксации сетки, как было рекомендовано в статье Amit'а выше, чтобы тайлы стали получаться более равномерными, и стало поменьше совсем крошечных или перекрученных тайлов. Но здесь-то я и уткнулся в неприятности. Что бы я ни пробовал, у меня не получалось удержать порядок построения выпуклой оболочки моим алгоритмом; он продолжал создавать перекрывающиеся или вообще развернутые треугольники то тут, то там, а порой и всюду. К тому же, я так и не смог научиться надежно избегать неимоверно коротких ребер между тайлами, и это часто смотрелось так будто четыре тайла соприкасаются в единой точке, хотя по факту соприкасались только два, а остальные просто едва заметно разделены соприкасающимеся тайлами. В ретроспективе, я думаю что у меня есть пара идей как избежать тех проблем, придерживаясь той же основной техники, но в то время я забросил это.
Подразделяемые Икосаэдры
Вместо этого, я решил начать со строго упорядоченной сетки, и затем шаг за шагом искажать ее пока она не станет по-настоящему неупорядоченной. Здесь отлично подходил подразделяемый икосаэдр, так как в нем не было проблем с искажением форм и размеров тайлов при масштабировании (Мне хотелось добавить лишь некрупные по масштабу искажения, и сохранить общую однородность). Поначалу, я разделял каждый из треугольников напрямую, и все точки, лежащие на одной плоскости я затем проецировал на сферу, но я выяснил что это создавало некоторые нежелательные крупномасштабные искажения. Позже я узнал что со сферической линейной интерполяцией, или slerp функцией, этого можно избежать, ура!
Также, я не хотел остаться в итоге с треугольными тайлами. Мне больше нравится гексагональная карта, где тайлы гарантированно не могут соприкасаться лишь одной точкой — соседние тайлы всегда имеют общее ребро. К счастью, треугольную сетку очень легко привести к точно такому же виду: попросту считаем каждую точку треугольной сетки тайлом, а каждый треугольник считаем углом тайла. Так получается двойственный многогранник (Также являющийся базисом для конвертации триангуляции Делоне в диаграмму Вороного). Вот схема, где первым идет обычный икосаэдр, вторым с гранями подразделенными на два сегмента, и третьим где они подразделены на восемь. Ниже показано, как каждый из них конвертируется в двойственный многогранник.
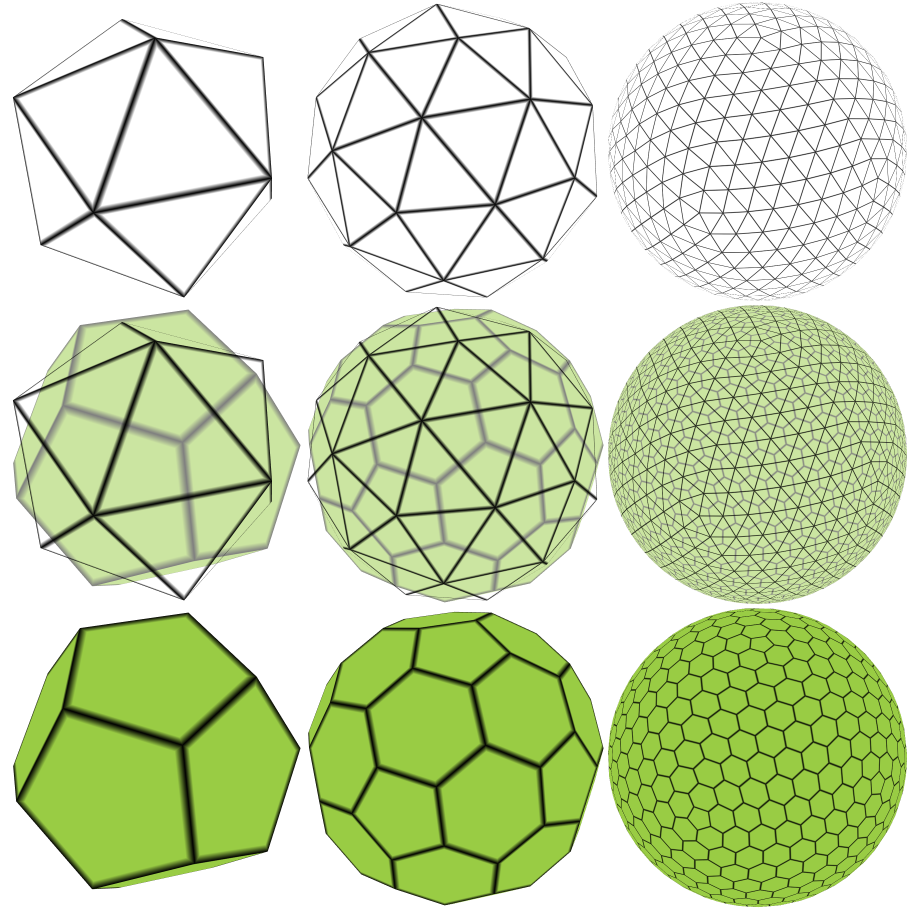
Подразделяемые икосаэдры, и соответствующие им двойственные многогранники
Заметим, что двойник обычного икосаэдра полностью состоит из пентагонов (из двенадцати, если быть точным; это додэкаэдр), на у более высоких подразделений практически одни гексагоны. По факту, неважно насколько подразделять, всегда будет оставаться ровно двенадцать пентагонов в фиксированных частях сетки, там где находились вершины изначального икосаэдра. Настало время добавлять иррегулярности.
К моему удовольствию, одна из функций которую я написал пока работал над алгоритмом выпуклой оболочки, делала как раз то что нужно для создания неравномерностей. Идея проста: находим два треугольника с общим ребром. Удаляем его, заменяя его на другое ребро, протянутое между двух точек, находящихся на противоположных концах этих двух треугольников. В некотором смысле, ребро оказывается повернуто, и топология сетки изменяется. Правда, это может привести к созданию чрезмерно тупоугольных треугольников, которые в свою очередь уродуют вид тайла. Так что мы несколько релаксируем сеть, пытаясь вытянуть эти треугольники обратно в приблизительно равномерную форму, при этом стараясь не сильно искажать соседние треугольники. Вот изображение этого процесса в действии, с примером как он влияет на тайлы, cформированные двойственным многогранником:
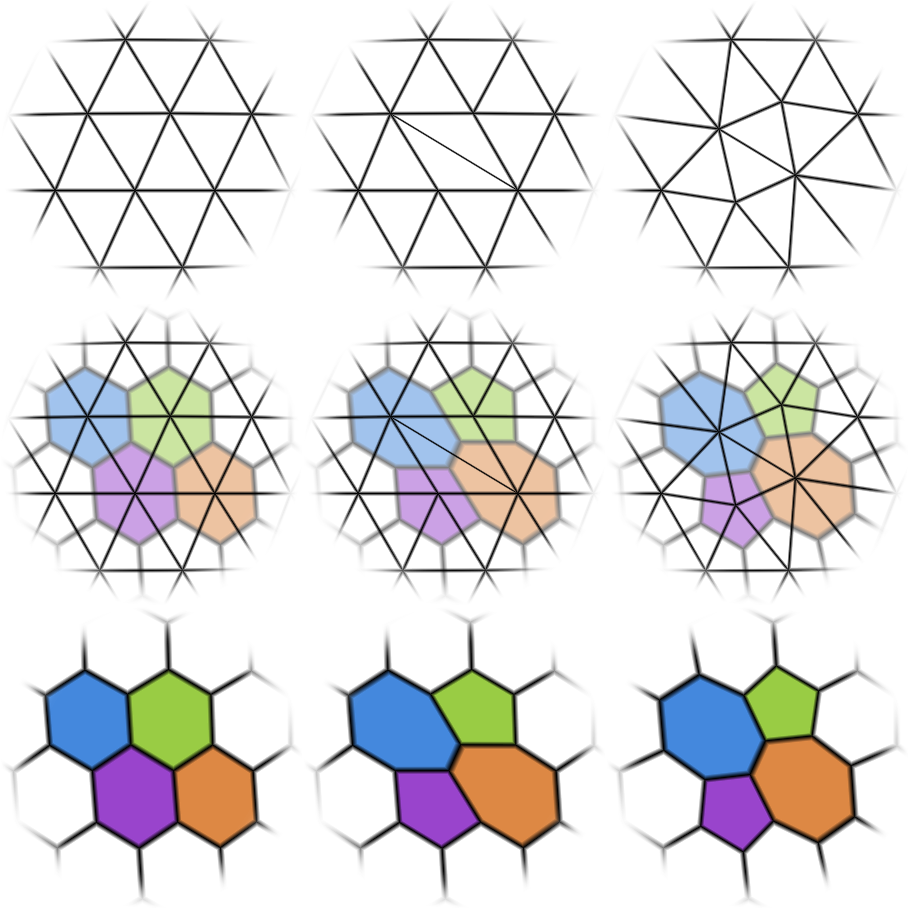
Вращение ребра для пертурбации топологии сетки
Заметим, что изначально все тайлы были гексагонами, но после трансофрмации два гексагона стали пентагонами, а другие два — гептагонами (семиугольниками). С использованием такой техники, численность пентагонов и гептагонов всегда будет сохранять баланс (хотя пентагонов будет ровно на двенадцать больше, чем гептагонов, благодаря изначальной дюжине). Однако если мы сделаем это на достаточном числе случайных ребер, то соотношение один-к-одному будет совсем не очевидным, а пентагоны с гептагономи будут перемешаны повсюду. Также этот подход позволяет мне увеличивать и уменьшать равномерность просто изменяя количество ребер, подвергаемое вращению. Ниже три примера искаженной сетки. На первой совсем мало вращений ребер, на второй — умеренное количество, там все еще можно разглядеть гексагональные паттерны, и на третьей примере вращений ребер очень много.

Слегка, умеренно и сильно искаженные сетки, все на основе подразделяемого икосаэдра
В моем конкретном использовании этой трансформации, я добавил несколько проверок случайного выбранного ребра перед тем как приступать к его вращению. Во-первых, если вращение сгенерирует тайл с более чем 7-ю или меньше чем 5-ю соседями, то такое ребро я отбрасываю и выбираю следующее случайное. Во-вторых, если длины исходного ребра и повернутого ребра слишком сильно различались, я отменял такое вращение, так как выходило бы, что я делаю и без того сильно искаженный сегмент сетки еще хуже. В-третьих, мне необходимо было убедиться, что ни один из исходных треугольников не имел тупых углов, примыкающих к общему ребру. Это добавило несколько тяжелых вычислений к проверке, но помогло избежать некоторых искажений сетки, от которых мне трудно было избавиться. Третья сетка на изображении сверху искажена максимально в пределах этих ограничений. Дальнейшие вращения ребер больше не приводят к значимому усилению иррегулярности.
И касательно релаксации сетки — я решил не проводить ее после каждого отдельного вращения ребра. Вместо этого, я делал пачку вращений, а потом проходил единой релаксацией по всей сетке. Дальше я делал еще несколько вращений, и повторял релаксацию. Я делал так 6 раз (произвольное число, выбранное эмпирически), а затем я несколько раз прогонял релаксацию пока сетка не достигала порога достаточной "расслабленности". Или, по крайней мере, пока релаксации не переставали фактически действовать, начиная вместо этого просто вращать сетку по кругу.
Также, я в итоге использовал другой метод, нежели чем алгоритм Ллойда. Тот требовал вычисления центров окружностей для каждого треугольника в триангуляции Делоне чтобы сгенерировать диаграмму Вороного, с последующим вычислением центроидов каждой ячейки на диаграмме, чтобы создать новую триангуляцию Делоне. Мало того, что это куча вычислений, так еще из-за моих искажений в сетке, центры окружностей бывали довольно дикими, особенно в тупоугольном треугольнике, когда центр вообще не находился в границах самого треугольника. Результатом часто были вырожденные, перекрывающиеся или развернутые треугольники, с которыми мне приходилось бороться ранее, и я начал осознавать, что именно центры окружностей создавали большую часть этих проблем.
Вместо этого я полностью сосредоточился на центроидах треугольников, которые гарантированно всегда оставались внутри его границ. Для каждого треугольника я вычислял расстояние от каждого угла до центроида. Я сравнивал эти расстояния с предварительно вычисленным идеальным расстоянием для равностороннего треугольника соответствующего размера, исходя из заданного размера площади поверхности планеты и количества треугольников. Затем я вытягивал или выталкивал углы чтобы приблизить их к этому идеальному расстоянию. (Всё же мне пришлось немного отступаться от идеального размера, иначе возникало слишком сильное давление на сетку, из-за которого некоторые треугольники полностью выворачивались, так как для них не хватало места.) Возможно, есть более правильное математическое объяснение, почему это работает, или другой подход, который бы позволил достичь того же концепта более эффективно, но и мой метод работал достаточно хорошо, так что я остался с ним.
После того, как я получал полностью релаксированную искаженную сетку, я генерировал двойственный многогранник, интерпретируя треугольники как углы тайлов, а вершины — как грани тайлов. (Ребра остаются, по существу, на прежних местах, хотя визуально они становятся более или менее ортогональными их исходному размещению, как вы можете видеть на некоторых изображениях выше.) Как уже упоминалось, общий подход для этого с помощью диаграммы Вороного — это использовать центры окружностей треугольников, но я опять же обнаружил, что с центроидами получалось более надежно. Хотя они и создавали некое визуальное растяжение, которое с центрами окружностей лучше удавалось избегать, но я осознал, что такие растянутые тайлы не были обязательно чем-то плохим; субъективно, тайлы на базе центроидов выглядели, пожалуй, даже лучше. И поскольку они также позволяли избегать диких выкручиваний тайлов в случае использования центров окружностей, я был в восторге и решил разбираться с оставшимися частями генерации планет.
Возвышенности
На этом этапе, чтобы сделать красивый скриншот для #ScreenshotSaturday в Твиттере, я использовал состряпанный на скорую руку вероятностый алгоритм заливки, чтобы создать участки земли и воды, раскрасив одни зеленым, а другие синим, с некоторыми случайными вариациями, чтобы добавить отличий. Это сработало достаточно хорошо для десяти минут, которые понадобились чтобы это закодить, но такого алгоритма было недостаточно чтобы создать интересные географические конструкции. Мне как минимум нужны были настоящие высоты.
Шум Перлина — распространенный алгоритм для такого типа задач, и мне уже доводилось играться с ним в прошлом. Но, по какой-то причине, я не решался идти по этому же пути. Хотя те структуры, что им генерируются, безусловно выходят сложными и интересными, в них все же присутствует определенный визуальный вкус, который является не совсем тем, что искал я. Шум Перлина имеет тенденцию быть чересчур равномерным, а я же хочу отчетливую географию с элементами, которые действительно выделяются. Например, горные хребты и цепочки островов, которые выглядят действительно уместно, а не являются случайным побочным продуктом бездумного алгоритма генерации высот.
Естественным образом, приходили в голову тектонические плиты, и я был достаточно смел, чтобы взяться за них. Честно говоря, в тот момент мне казалось что этот подход мог быть одним из более быстрых путей для получения интересной географии, в сравнении с использованием шума Перлина. В конечном счете, это оказалось не совсем так, но плиты все же сработали впечатляюще, несмотря на то, что я не до конца понимал, что же я делаю.
Первым шагом было определить, собственно, плиты. Для этого я выбирал фиксированное число случайных начальных тайлов, а затем просто проводил случайную заливку с ними всеми одновременно. Когда каждый тайл планеты наконец принадлежал какой-либо тектонической плите, я вычислял несколько других случайных параметров каждой плиты, которые будут отражать их движение и другие атрибуты. Первым параметром была ось, проходящая сквозь центр планеты, вокруг которого плита движется, а также небольшой угол, задающий скорость движения. Обычно это представляло из себя дрейфующее движение, хотя оно может создавать и движение вращательного типа, если ось проходит через саму плиту. Вторым параметром был еще один небольшой угол, представляющий скорость вращения вокруг произвольно выбранной центральной точки плиты. Вместе эти два параметра давали каждой тектонической плите случайное количество дрейфа и вращения, которые естественным образом создавали бы конфликтующие движения границ плит относительно друг друга. В дополнение к движению, я случайно помечал плиту как океаническую или нет, а затем случайно выбирал желаемую высоту плиты. Эта высота находилась в пределах определенного позитивного диапазона для наземных плит и отрицательного диапазона для океанических. (Конечно, плавающие океаны с водопадами в милю высотой были бы великолепны, но давайте пока придерживаться благоразумных алгоритмов.)
Следующим шагом было взять движения плит и вычислить тип и степень напряженности в каждой точке вдоль их границ. Для каждой точки соприкосновения я рассчитал движения каждой из плит в этой конкретном месте. Результат их вычитания давал мне относительное движение. Затем я выделял из этого движения составной элемент, который ровно перпендикулярен границе плиты в этом месте. Он и соответствовал количеству относительного движения, которое непосредственно толкало пластины друг на друга, или же оттягивало их в разные стороны. Это я определил как давление, которое могло быть как положительным (столкновение) или отрицательным (разделение). Я также определил относительное движение, которые было параллельно границе, как сдвиг (только сама величина этого движения была важна, так что сдвиг был строго неотрициательным).
Тектонические плиты, их движение и напряженности вдоль границ
После того, как были вычислены тип и степень напряженности вдоль границ плиты, я использовал эту информацию для задания высоты в каждой граничной точке. Для точек, где положительное давление было особенно заметным, я вначале проверял, являются ли обе плиты океаническими или сухопутными. Если они были одинаковыми, то я относился к ним как к напрямую сталкивающимся, брал максимальную высоту из двух плит, а затем добавлял еще некоторую величину для создания горного хребта. Если же сталкивались океаническая и сухопутная плиты, я предполагал, что океаническая плита уходит под земную плиту, и корректировал расчеты высоты. Для взаимодействий с отрицательным давлением или сдвигом, я попросту использовал максимальную из высот и создавал более слабое возвышение, вне зависимости от типа вовлеченных плит. Для границ же, где напряженности всех видов были достаточно низкими, я просто усреднял высоты обеих плит и устанавливал результат как высоту границы.

Высоты, рассчитанные исходя из взаимодействий тектонических плит.
Когда наконец все тектонические взаимодействия определены и граничные высоты вычислены, настало время вычислять высоты всех внутренних точек каждой из плит. Здесь я использовал очередь с приоритетом для обработки точек в порядке удаления их от границ. Для каждой точки я использовал расстояние до границы, расстояние до центра плиты и высоту и уровень тектонической активности ближайшей границы для определения возвышенности этой точки. Большая часть тектонической активности генерировала достаточно простую кривую возвышенностей, которая интерполировалась от границы к центру. Сухопутные плиты с океаническими плитами, подлезающими под них, имели несколько иную кривую, начинающуюся с более низкой отметки, быстро поднимающейся в горный хребет, а затем снова опускающуюся до общей высоты плиты. Вдохновлялся я картинками из Википедии про конвергентные границы.
В итоге, я думаю, я внес достаточно допущений и неточностей, чтобы геологи словили с моего решения двойной фейспалм. Но кого это волнует? У меня теперь клёво выглядящие континенты! Ну, то есть, их заготовки.
Погода
Покраска растительности, гор и океанов, базирующаяся на одном только уровне высот, была достаточной, чтобы снова дать мне хорошую картинку для Твиттера. Но всё еще не хватало пустынь, лесов, джунглей и других разнообразных биомов. Чтобы осилить эту задачу, я решил что мне понадобятся расчеты воздушных потоков, распространяющие тепло и влагу вокруг, и понимание, как влага будет зависеть от высот на пути своего следования, постепенно превращаясь в осадки. К счастью, я не чувствовал себя обязанным придерживаться реалистичной симуляции воздушных потоков. Вместо этого я просто выбрал несколько случайных точек на земном шаре, и назначил их центральными точками вокруг которых воздух будет перемещаться, без затей, по кругу. Однако всё же если две круговых структуры накладывались, то я рассчитывал средневзвешенное значение, чтобы определить окончательное направление и интенсивность воздушного потока в этой точке. Благодаря тщательному отбору точек на сфере, а также некоторому случайному отклонению их местоположения, силы и масштаба влияния, я в итоге получил структуры воздушных потоков, которые казались хорошим компромиссом между упорядоченностью и хаотичностью.
Добавление тепла и влаги в расчеты оказалось сложнее, чем я ожидал. Идея была довольно проста: за один проход сгенерировать некоторое количество тепла и влаги в каждой точке планеты, а затем в несколько проходов перемещать тепло и влагу согласно движению воздушных потоков, пока всё оно не будет распределено. Оказалось что этот хитрый процесс сложно провернуть правильно, особенно когда приходится жонглировать параметрами энергий, расстояний, площадей, скоростей и масс. И всё это просто машинные числа с плавающей точкой без привязки к конкретным физическим величинам. Мне было лениво, я подгонял значения возводя в степень и деля числа по мере необходимости, чтобы прийти к более-менее рабочему варианту. Полагаю, всё это нужно когда-нибудь взять и переписать с нуля. Тем не менее, как и в большей части вышеописанной работы, в итоге цели были достигнуты в удовлетворяющем меня на тот момент объеме.
В моей реализации я вначале вычислял тепло. В каждой точке генерировалось одинаковое количество тепла (что, теперь как я понимаю, было глупо; как минимум, полярные регионы абсорбировали бы меньше тепла от звезды). Затем я весьма упрощенно распределял его вокруг — каждая точка поглощала столько движущегося мимо тепла, сколько могла, что зависело от скорости воздуха (более низкая скорость давала больше времени на поглощение большего тепла). Наконец, используя поглощенное количество тепла, высоту, и гео широту каждой точки, я вычислял итоговую температуру, вписанную в свою собственную температурную шкалу от -2/3 до +1, с 0 в качестве точки замерзания.

Температура, определенная на основе воздушных потоков, высоты и гео координат
Когда с температурой всё стало определено, она была использована для вычисления распределения влажности по тайлам. Сухопутные тайлы не производили влаги; они только потребляли её. Океанические тайлы производили влагу в зависимости от своего размера и температуры. Более горячие зоны испаряли больше влаги в воздух, нежели чем холодные области. (Как и в случае с геологами, уверен, сейчас я раздражаю метеорологов. Пусть посочувствуют друг другу). Дальше влага распространяется аналогично теплоте, но с некоторыми дополнительными условиями для высоты и температуры (большая высота и меньшая температура вызовет больше осадков. В результате воздух, поступающий на сушу с океана, будет нести много влаги. Если воздушные массы движутся над большими равнинными областями, то больше количество влаги будет продвигаться вглубь материка, и всюду будет достаточное количество осадков, пока воздух не станет слишком сухим. Однако если воздух проходит над горным хребтом, он имеет тенденцию быстро проливаться осадками, и в результате земля по ту сторону хребта оказывается заметно суше. Это явление известно как дождевая тень.

Влага, определенная на основе воздушных потоков, водных массивов, температуры и высоты
Биомы
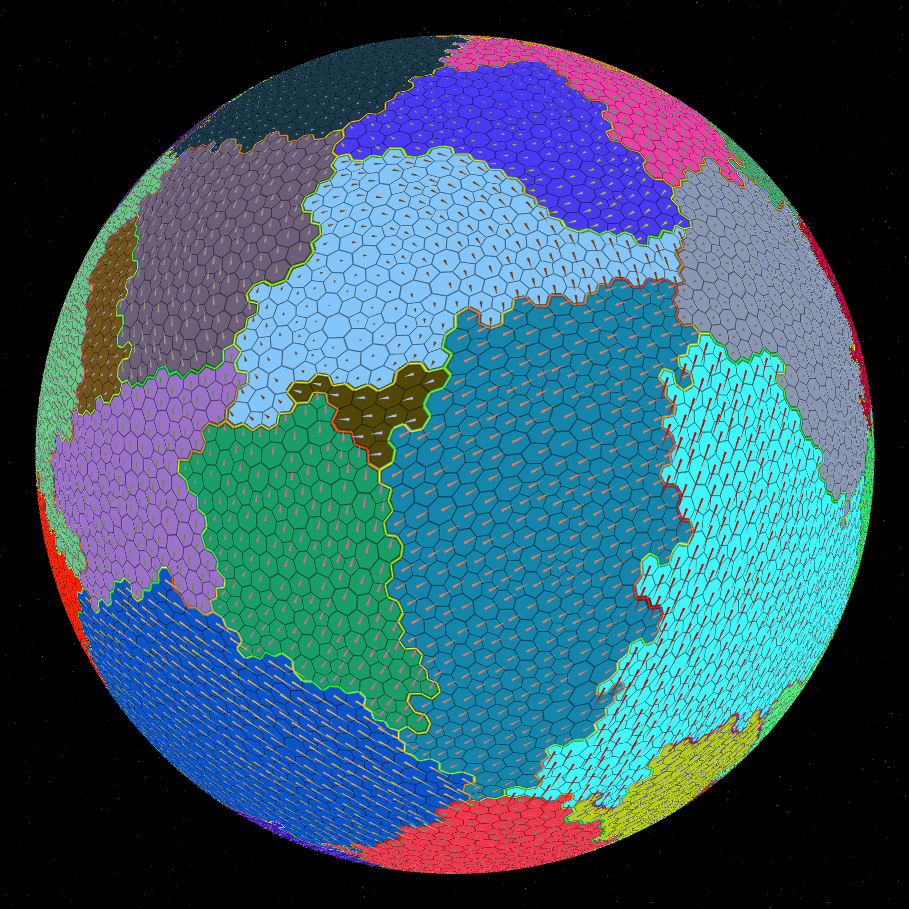
Теперь, когда у меня были высота, температура и осадки, я решил, что получил достаточно данных для генерации интересных биомов. Эту функциональность можно было бы дорабатывать бесконечно, но я собрал несколько правил, которые определяли, какой из небольшого набора биомов назначается тайлу, исходя из этих трех параметров. Низинные теплые регионы с малым количеством осадков становились пустынями, а с большим количеством — тропическами лесами. Низинные умеренные регионы со средним количеством осадков становились пастбищами. Холодные регионы с низкой влажностью становились тундрой. Высотные регионы превращались в скалистые горы или снежные гор в зависимости от температуры и количества осадков. И так далее. Это дало мне необходимое разнообразие для создания примеров планет (см ниже), и более-менее отражает ту версию, которая публично доступна на моем вебсайте.

Планета высокой детализации

Планета средней детализации

Планета низкой детализации, без искажений топологии оригинального подразделяемого икосаэдра. Посмотрите на отвратительно вклинившийся пентагон, немного справа снизу от центра
Код, Библиотеки, и прочие мелочи
100% кода написано на JavaScript, загрузить его можно здесь. В качестве обертки над WebGL применяется three.js. Он довольно легок в использовании, и давал мне простой доступ к буферам вершин и треугольников, что отлично подходит для процедурно сгенерированной геометрии. Документация имеет пробелы, и отчасти устаревшая, но быстрый взгляд в исходники обычно проясняет ситуацию. Это мой первый проект в области WebGL, и я получил удовольствие от этого опыта.
Я по-прежнему использую jQuery для манипуляций с HTML. Здесь я впервые использовал HTML как оверлей над canvas-ом, и меня очень радует, что такая техника позволила применить мои навыки владения HTML для создания UI в околоигровом окружении. А в сочетании с jQuery всё вышло еще лучше.
Я по-прежнему мечтаю чтобы Lua стал языком веба вместо JavaScript. Разочаровывает невозможность использовать ссылку на объект как ключ внутри объекта-словаря. Впрочем, я адаптировал свои конструкции чтобы это компенсировать, так что это не стало серьезным препятствием для проекта (хотя пришлось повозиться). Что реально зацепило меня в этот раз, так это исключительно однопоточная модель исполнения JavaScript. Первоначально все процессы, описанные выше исполнялись в рамках единственной функции generatePlanet(). Как только вычисления стали достаточно сложными, это начало приводить к тому что браузер могут убить всю страницу потому что полагал, что страница зависала перманентно. Это также означало что у меня не было надежды на реализацию индикатора прогресса, не говоря уже о возможности отмены процесса генерации планеты.
Конечно, Lua тоже не имеет поддержки работы с потоками "из коробки", и скорее всего имел бы схожую однопоточную модель, если бы был реализован в браузерах. Но что в нем есть уже давно так это корутины — то что в JavaScript еще неизвестно появится ли в хоть сколько-нибудь обозримом будущем (И кто знает, сколько еще времени потребуется чтобы их начал поддерживать Internet Explorer). С корутинами, я смог бы держать код чистым, действуя как бы в одном потоке, но применяя yield в уместные моменты, позволяя браузеру заняться своими делами, прежде чем вернуть контроль моей длительной операции.
В качестве альтернативы, я написал свою собственную утилиту для этого. JavaScript хотя бы поддерживает обращение с функциями как с объектами, анонимные функции и замыкания. Это позволило мне создать систему, где каждая функция может либо выполнять работу, либо может зарегистрировать дополнительные функции которые вместе выполняют эту работу. Каждая функция может запускаться один раз, или несколько раз, как в цикле, пока вся ее работа не будет выполнена. Также, каждая функция способна сообщать относительную долю собственной работы по сравнению с долями других соседних функций, а также насколько далеко зашло её выполнение (предполагая, что это известно; иногда бывает трудно оценить прогресс в достижении конечного условия). Это позволяет проводить достаточно эффективный подсчет прогресса даже для крайне разнородных вычислений. Если захотите взглянуть, у меня в исходниках эта утилита названа SteppedAction.
Итог
Я наконец дал себе высказаться, так что на этом и заканчивается пост в блоге. Но это не конец для генератора планет. Теперь я вернусь к играм, и попробую применить генератор для проверки и прототипитрования некоторых моих идей касательно игровых механик. Хотя изначально он и был задуман для использования в игре типа civilizaition-песочницы, я подумываю сейчас о сочетании стратегии с развитием городов как в Civilization, с более простым и быстрым стратегическим геймплеем игр серии Warlords от Steve Fawkner. Я думаю, мне следует контролировать собственный полет мыслей, и придерживаться более разумных и достижимых целей, прежде чем я осилю движение к самым высоким и амбициозным целям. Даже в этому случае, никаких обещаний, как долго у меня займет создать нечто, что я готов буду показать, не даю; такие вещи не предсказать.
Однако, возможно я не удержусь от работы над 2-й версией генератора планет. Оптимизировать некоторы алгоритмы, исправить часть моих ошибок, добавить в ландшафт реки. Опять же, никаких обещаний, но вы также можете следить и за этим (пригодится мой RSS фид). Подпишитесь на меня в Твиттере (@AndyGainey), и вы скорее всего сможете увидеть превьюшки задолго то того, как я соберусь выложить их на своем сайте.



Комментариев нет:
Отправить комментарий