В Steam появились новые игры от Electronic Arts

4 июня 2020 года в сервисе Steam неожиданно для многих пользователей стали доступны сразу более десятка новых игр от Electronic Arts (+13 на данный момент). Также с 5 июня 2020 года игрокам стало доступно переиздание Command & Conquer и Red Alert в разрешении 4K от бывших сотрудников Westwood Studios.
Компании Electronic Arts и Valve заключили партнерство в прошлом году, но тогда его плодом стал выпуск в Steam в ноябре 2019 года игры «Звездные Войны Джедаи: Павший Орден». И после этого момента в Steam новые игры от EA не выходили.

Однако, спустя 6 месяцев, в начале июня 2020 года сразу тринадать игр от EA, помимо переиздания Command & Conquer и Red Alert, стали доступны пользователям:

• Dragon Age 2;
• Crysis 3;
• Need for Speed Heat;
• Plants vs. Zombies: Битва за Нейборвиль!;
• Need for Speed Rivals;
• Need for Speed (2015);
• Unravel;
• Unravel Two;
• Sea of Solitude;
• Dragon Age: Inquisition;
• Fe;
• Burnout Paradise Remastered;
• Mirror's Edge Catalyst.

Согласно информации портала VentureBeat, в ближайшее время добавит EA еще добавит в Steam и другие свои игры, например, некоторые части Battlefield, Titanfall 2 и The Sims 4. Также ЕА и Valve подтвердили, что скоро в Steam появится и платная подписка EA Access, которая дает доступ к эксклюзивным пробным версиям некоторых игр компании, а также скидки на покупки.

Ранее в конце мая 2020 года открыла для игрового сообщества и энтузиастов исходные коды игр Command & Conquer: Tiberian Dawn и Red Alert из обновленной редакции (Remastered Collection). Исходные тексты базовых библиотек TiberianDawn.dll и RedAlert.dll опубликованы под лицензией GPLv3 и доступны на GitHub. Таким образом, легендарная Command & Conquer стала первой из знаменитых игр в жанре RTS (стратегия в реальном времени), код которой теперь доступен под свободной лицензией.

Let's block ads! (Why?)

[Перевод] Две ошибки Эйнштейна

Привет, читатель! Меня зовут Ирина, я веду телеграм-канал об астрофизике и квантовой механике «Quant». Хочу поделиться с вами переводом статьи об ошибках, которые допустил Альберт Эйнштейн в процессе научной деятельности. В чем-то он признал свою неправоту, а с чем-то наотрез отказался соглашаться.

Приятного чтения!

Гравюра на дереве из книги Камилля Фламмариона 1888 года «L'Atmosphère: météorologie populaire». Подпись гласит: «Миссионер Средневековья говорит, что он нашел точку, где соприкасаются небо и земля», и продолжает: «Что же тогда есть в этом голубом небе, которое, несомненно, существует и которое закрывает звезды днем?»
Научное исследование основывается на соотношении между реальностью природы, как она наблюдается, и представлением этой реальности, сформулированным теорией на математическом языке. Если все следствия теории экспериментально доказаны, то она считается обоснованной. Этот подход, который использовался в течение почти четырех столетий, создал последовательный свод знаний. Но эти успехи были достигнуты благодаря интеллекту человеческих существ, которые, несмотря ни на что, могут держаться за свои ранее существовавшие убеждения и предубеждения. Это может повлиять на прогресс науки, даже на величайшие умы.

Первая ошибка

В своем главном труде по общей теории относительности Эйнштейн написал уравнение, описывающее эволюцию Вселенной во времени. Решение этого уравнения показывает, что Вселенная нестабильна, а не представляет собой огромную сферу с постоянным объемом, вокруг которой скользят звезды, как считалось в то время.

В начале XX века люди жили с устоявшейся идеей статичной Вселенной, в которой движение звезд никогда не меняется. Это, вероятно, связано с учением Аристотеля, утверждающего, что небо неизменно, в отличие от Земли, которая тленна. Эта идея вызвала историческую аномалию: в 1054 году китайцы заметили появление нового света на небе, но ни один европейский документ не упоминает об этом. Тем не менее его можно было увидеть даже днем, и оно продолжалось несколько недель. Это была сверхновая, то есть умирающая звезда, остатки которой до сих пор можно рассматривать как Крабовидную туманность. Господствующая в Европе мысль не позволяла людям принять явление, которое так сильно противоречило идее неизменного неба. Сверхновая — это очень редкое явление, которое можно наблюдать невооруженным глазом лишь раз в столетие. Самое последнее из них датируется 1987 годом. Так что Аристотель был почти прав, полагая, что небо остается неизменным — по крайней мере, в масштабе человеческой жизни.

Чтобы оставаться в согласии с идеей статичной Вселенной, Эйнштейн ввел в свои уравнения космологическую постоянную, которая заморозила состояние Вселенной. Его интуиция сбила его с пути истинного: в 1929 году, когда Хаббл продемонстрировал, что Вселенная расширяется, Эйнштейн признал, что совершил «свою самую большую ошибку».

Квантовая случайность

Квантовая механика развивалась примерно в то же время, что и теория относительности. Она описывает физику в бесконечно малом масштабе. Эйнштейн внес большой вклад в эту область в 1905 году, интерпретируя фотоэлектрический эффект как столкновение электронов и фотонов — то есть бесконечно малых частиц, несущих чистую энергию. Другими словами, свет, который традиционно описывается как волна, ведет себя как поток частиц. Именно этот шаг вперед, а не теория относительности, принес Эйнштейну Нобелевскую премию в 1921 году.

Но, несмотря на этот жизненно важный вклад, он упрямо отвергал ключевой урок квантовой механики — что мир частиц не связан строгим детерминизмом классической физики. Квантовый мир вероятностен. Мы знаем только, как предсказать вероятность возникновения события среди целого ряда возможностей.

Крабовидная туманность, наблюдаемая сегодня на разных длинах волн, не была зарегистрирована европейцами, когда она появилась в 1054 году. Картинки слева направо: вид в радиоволнах, инфракрасных лучах, видимом свете, ультрафиолетовых лучах, рентгеновских лучах, гамма-лучах.

В слепоте Эйнштейна мы снова видим влияние греческой философии. Платон учил, что мысль должна оставаться идеальной, свободной от случайностей действительности — благородная идея, но не подчиняющаяся предписаниям науки. Знание требует совершенной согласованности со всеми предсказанными фактами, тогда как вера основана на вероятности, порожденной частичными наблюдениями. Сам Эйнштейн был убежден, что чистая мысль способна полностью охватить реальность, но квантовая случайность противоречит этой гипотезе.

Эйнштейн не принял этот фундаментальный индетерминизм, который был сформулирован его провокационным приговором: «Бог не играет в кости со Вселенной». Он представлял себе существование скрытых переменных, то есть еще не открытых чисел за пределами массы, заряда и спина, которые физики используют для описания частиц. Но эксперимент не поддержал эту идею. Нельзя отрицать, что существует реальность, которая превосходит наше понимание — мы не можем знать все о мире бесконечно малого.

Случайные прихоти воображения

В процессе научного метода все еще существует стадия, которая не является полностью объективной. Это то, что приводит к концептуализации теории, и Эйнштейн со своими мысленными экспериментами подает знаменитый пример этого. Он заявил, что «воображение важнее знания». Действительно, рассматривая разрозненные наблюдения, физик должен представить себе лежащий в их основе закон. Иногда несколько теоретических моделей соревнуются в объяснении того или иного явления, и только в этот момент логика снова берет верх.

«Роль разума состоит не в том, чтобы обнаружить, а в том, чтобы подготовиться. Это хорошо только для служебных задач» (Симона Вейл, «Гравитация и грация»).

Таким образом, прогресс идей проистекает из того, что называется интуицией. Это своего рода скачок в познании, который выходит за пределы чистой рациональности. Грань между объективным и субъективным уже не является полностью твердой. Мысли исходят от нейронов под действием электромагнитных импульсов, причем некоторые из них особенно плодородны, как будто между клетками происходит короткое замыкание, где действует случайность.
Но эти интуиции, или «цветы» человеческого духа, не одинаковы для всех — мозг Эйнштейна произвел «E=mc²», тогда как мозг Пруста придумал замечательную метафору. Интуиция возникает случайно, но эта случайность ограничена опытом, культурой и знаниями каждого человека.

Результат эксперимента Юнга с интерференцией: картина формируется бит за битом с приходом электронов (8 электронов на фото a, 270 электронов на фото b, 2000 на фото c и 60 000 на фото d), которые в конечном итоге образуют вертикальные полосы, называемые интерференционными полосами.

Преимущества случайности

Это не должно быть шокирующим известием о том, что существует реальность, не постигаемая нашим собственным разумом. Без случайности мы руководствуемся нашими инстинктами и привычками, всем, что делает нас предсказуемыми. То, что мы делаем, ограничивается почти исключительно этим первым слоем реальности, с обычными заботами и обязательными задачами. Но есть и другой слой реальности, тот, где очевидная случайность является отличительной чертой.

«Никогда административные или академические усилия не заменят чудес случайности, которыми мы обязаны великим людям» (Оноре де Бальзак, «Кузен Понс»).

Эйнштейн — пример изобретательного и свободного духа, но он все же сохранил свои предубеждения. Его «первую ошибку» можно резюмировать словами: «Я отказываюсь верить в начало Вселенной». Однако эксперименты доказали, что он ошибался. Его вердикт о том, что Бог не играет в кости, означает: «Я отказываюсь верить в случайность». Однако квантовая механика предполагает обязательную случайность. Его предложение ставит вопрос о том, будет ли он верить в Бога в мире без случайностей, что значительно ограничило бы нашу свободу, поскольку мы тогда были бы ограничены в абсолютном детерминизме. Эйнштейн был упрям в своем отказе. Для него человеческий мозг должен быть способен знать, что такое Вселенная. С гораздо большей скромностью Гейзенберг учит нас, что физика ограничена описанием того, как природа реагирует в данных обстоятельствах.

Квантовая теория показывает, что полное понимание нам недоступно. В свою очередь, она предлагает случайность, которая приносит как разочарования и опасности, так и выгоды.

«Человек может избежать законов этого мира только на мгновение. Мгновения паузы, созерцания, чистой интуиции… именно с этими вспышками он способен на сверхчеловеческое» (Симона Вейл, «Гравитация и грация»).

Эйнштейн, легендарный физик, является прекрасным примером творческого существа. Поэтому его отказ от случайности — это парадокс, потому что именно случайность делает возможной интуицию, допускающую творческие процессы как в науке, так и в искусстве.

Let's block ads! (Why?)

Правообладатели постарались: с YouTube могут исчезнуть музыкальные видеоуроки с разборами чужих композиций

Повсеместная самоизоляция, вызванная пандемией, приковала миллионы глаз к мониторам. Многие нашли отдушину в виде обучения, в частности, игре на музыкальных инструментах. Возросший интерес к обучающему музыкальному контенту обострил проблемы, связанные с авторскими правами на композиции, разборами которых занимаются некоторые видеоблогеры. Под очередную раздачу юридических панчей попали именно т.н. разборщики — музыкальные блогеры (чаще гитарные), демонстрирующие новичкам как сыграть их любимые композиции каких-нибудь Metallica или Radiohead. Их деятельность за последние 10 лет превратилась в своеобразную индустрию, которую сегодня может уничтожить применение неоднозначных норм авторского права.

Блогеры отмечают, что YouTube всё чаще блокирует видео с разборами известных произведений. Это происходит как по прямым жалобам правообладателей, так и в результате действия поисковых алгоритмов, обнаруживающих в видео фрагменты композиций, защищенных авторским правом. Под катом мои мысли о проблеме, а также мнение гитарного блогера, преподавателя и музыканта Юрия (Fredguitarist) Шильникова по поводу проблемы и её возможного решения.

Что происходит?

Разборщики на YouTube столкнулись с тем, что их видео стали чаще блокировать c формулировкой “нарушение авторских прав”. Такое происходило и раньше, однако санкции в отношении разборщиков были менее жесткие и, как правило, для видео просто отключалась монетизация. Сегодня же контент блокируется, а при троекратном грубом нарушении удаляется весь канал обзорщика.

Ситуация доходит до абсурда, например, как сообщают www.guitarworld.com,
совместное видео легендарного сессионного басиста Лиланда Склар (Leland Sklar) и фолкового гитариста Джеймса Тейлора с их собственным произведением попало под ограничительные меры хостинга.

Оказалось, что по договорным обязательства все творческие продукты Тейлора принадлежат третьей стороне. Именно на основании жалобы некоего третьего правообладателя, имеющего права на контент Тейлора, YouTube удалил совместное видео музыкантов, проигнорировав таким образом права и желание самих авторов.

Не менее комична ситуация с гитарным блогером Родни Мак Ги (Rodney McG), которого цитирует www.guitarworld.com, он также получил страйк на собственное произведение, которое было перезалито в другой аранжировке. По его словам, видео было удалено со ссылкой на требование автора, хотя он от хостинга ничего не требовал. Он даже решил записать цикл роликов по этому поводу.

“Пандемический невроз правообладателей" также коснулся кавер-версий. В последние полгода музыкальные коллективы и исполнители, публикующие каверы на их любимые группы, часто с разрешением самих коллективов стали значительно чаще получать претензии от сервиса.

Как сообщают источники близкие к администрации YouTube, в сервисе также не очень довольны положением вещей. С одной стороны они вынуждены соглашаться с законными требованиями правообладателей и защищают таким образом интересы некоторой части крупных клиентов. С другой — жесткие меры в отношении такого контента приводят к его сокращению, а соответственно снижению количества просмотров, низкой лояльности пользователей, уменьшению прибыли от размещения рекламы, а также к банальному перерасходу ресурсов на обеспечение политики в области авторских прав.

К чему это может привести?

Учитывая существующую юридическую практику и позицию, которую обычно занимает крупнейший видеохостинг планеты, я попробую немного поиграть в бабушку Вангу и сделать прогноз о развитии ситуации.

Оптимистичный сценарий предполагает, что всё останется как есть и в дальнейшем политика YouTube не будет ужесточаться, и действуя в рамках существующего неуклюжего и неоднозначного законодательства об авторском праве, сервис не станет вредить себе.

Таким образом к концу массовой самоизоляции фокус правообладателей сместится, а обзорщиков и кавероделов оставят в покое, лишь изредка бросая страйки на откровенно криворукие разборы песен и бездарные ужасные каверы. Последние, ввиду низкого качества, явно не будут соответствовать понятиям о добросовестном использовании, а соответственно, их не жалко. Я нахожу, что этот сценарий возможен в силу того, что сам сервис заинтересован в максимальном разнообразии качественного контента.

Пессимистичный сценарий предполагает применение правила о 15 секундах (разрешение использования не более 15 секунд композиции, а также детальный подход к вопросу упущенной выгоды (убытков) правообладателя. Т.е., если правообладатель гипотетически мог потерять средства, то считается, что он понес убытки от публикации. При этом будет нивелироваться либо игнорироваться всё, что может отнести контент к категории добросовестного использования.

В итоге, обучающий контент с разбором композиций смогут выкладывать только сами авторы произведений и только в том случае, что прочие правообладатели, типа продюсерских центров или звукозаписывающих компаний не возражают. Это колоссально сократит количество каналов такого рода и фактически убьет одну из отраслей ютьюб блогинга. В первую очередь от такого развития событий пострадает сам сервис, останутся недовольными пользователи.

Музыканты также вряд ли серьезно увеличат прибыль, при этом смогут в полной мере ощутить, что их контрактные ограничения распространяются также и на ютьюб. Как мне кажется в пессимистичном сценарии в выигрыше будут только сторонние правообладатели, которые зарабатывают на рекламе и продаже музыки, но не имеют прямого отношения к её созданию.

Утопический сценарий. Создатели музыки и блогеры смогут продавить реформирование мировой системы авторского права по причине её неработоспособности и абсурдности. Это приведет к созданию новой системы авторского права, предполагающей справедливое вознаграждение для авторов при возможности свободного использования контента. Продавцам контента придется адаптироваться к новой системе, отказаться от старых форм работы и поступиться существенной частью доходов в пользу музыкантов и общества.

Специальное мнение от Fredguitarist

О решении проблемы с авторскими правами для разборщиков я спросил основателя и гитариста группы JASE, «отца» российского гитарного ютьюба — Юрия Шильникова, боле известного как Fredguitarist. Далее его точка зрения.

На самом деле вопрос очень непростой, на первый взгляд, я здесь вижу два решения:

1) Деление монетизации пополам, ведь очевидно, что автор, разбирая популярную песню, набирает себе таким образом просмотры и повышает вероятность записи к себе на уроки (если таковые имеются) или продажи рекламы на своем канале, но с другой стороны, он тоже проделывает определенную работу и, возможно, потенциально увеличивает популярность этой песни.

2) Выдача лицензий на разборы, понятно, что это весьма трудно реализовать, но вроде есть кавер-группы, работающие по лицензии, значит потенциально это реально. Очевидно, что во многих случаях уровень разборщика настолько низок, что любой профессиональный музыкант лишь снисходительно улыбнётся, увидив такой разбор. Тем не менее, крайне низкий уровень разборщика может резко негативно сказаться на начинающих гитаристах, ведь многие новички думают, что раз так показывают «с экрана» то значит так и надо.

В качестве заключения

Я искренне надеюсь, что со временем найдётся взаимовыгодное и справедливое решение проблем, связанных с разборами и с авторскими правами. Очевидно, что для этого у законодателей во всём мире должно созреть понимание неактуальности и неэффективности существующей системы авторского права. Я буду искренне признателен за ваше мнение в комментариях и участие в небольшом опросе.

Традиционная реклама
Этот блог существует благодаря тому, что мы продаём аудиоаппаратуры, музыкальные инструменты и много другой полезной электроники. В нашем каталоге вы найдёте усилители, акустические сиcтемы, наушники, телевизоры и многое другое

Let's block ads! (Why?)

Аллокаторы памяти

Всем привет! Не так давно, после очень плотного изучения аллокаторов и алгоритмов распределения памяти, а также в последующем применении их на практике мне в голову пришла идея написать статью, в которой будет максимально подробно рассказано о них. Считаю, что данная тема будет достаточно востребованной, так как в сети, особенно в русскоязычной части, на данный момент существует очень мало источников, посвященных этому вопросу.

Предисловие

Для начала, хотелось бы сразу отметить, что если кто-то впервые слышит термины «аллокатор», «алгоритмы распределения памяти» и не понимает, для чего это все нужно, то тогда, прежде чем читать данную статью, я рекомендую ознакомиться с данным источником. В данной статье достаточно хорошо рассказывается, какие существуют проблемы в стандартных аллокаторах памяти, и для каких целей стоит использовать другие способы распределения памяти, помимо стандартных. Здесь же я буду рассказывать только о самих алгоритмах распределения, ну и, конечно же, в конце приведу реализацию одного из аллокаторов, которая может быть без проблем использована в стандартных контейнерах С++.

Основы

Концептуально выделяется пять основных операции, которые можно осуществить над аллокатором (хочется отметить, что не все аллокаторы могут явно соответствовать этому интерфейсу):

• create – создает аллокатор и отдает ему в распоряжение некоторый объем памяти;
• allocate – выделяет блок определенного размера из области памяти, которым распоряжается аллокатор;
• deallocate – освобождает определенный блок;
• free – освобождает все выделенные блоки из памяти аллокатора (память, выделенная аллокатору, не освобождается);
• destroy – уничтожает аллокатор с последующим освобождением памяти, выделенной аллокатору.

Linear Allocator

Linear Allocator, он же «линейный» — это самый простой вид аллокаторов. Идея состоит в том, чтобы сохранить указатель на начало блока памяти выделенному аллокатору, а также использовать другой указатель или числовое представление, которое необходимо будет перемещать каждый раз, когда выделение из аллокатора завершено. В этом аллокаторе внутренняя фрагментация сведена к минимуму, потому что все элементы вставляются последовательно (пространственная локальность), и единственная фрагментация между ними — выравнивание.
Дальше предлагаю рассмотреть несколько примеров, в которых будет наглядно показано в деталях, как работает данный аллокатор. Возьмем некоторый блок памяти равный 14 байтам и отдадим его в управление аллокатору. Как видно из картинки ниже, мы сохраняем указатель на начало памяти (start), а также храним два указателя, либо два числовых представления, которые содержат информацию об общем (end) и используемом (used) размерах памяти.

Представим, что в аллокатор поступил запрос на выделение 4 байт памяти. Действия аллокатора на исполнения этого запроса будут следующие:

• проверить достаточно ли памяти для выделения;
• сохранить текущий указатель used, который в дальнейшем будет отдан пользователю, как указатель на блок выделенной памяти из аллокатора;
• сместить указатель used на величину равную объему выделенного блока памяти, т.е. на 4 байта.

Дальше, например, приходит запрос на выделение 8 байт и, соответственно, действия аллокатора будут точно такими же вне зависимости от размера выделяемого блока памяти.

А вот здесь уже будет немного интереснее, например, если приходит запрос на выделение только 1 байта, и если мы не хотим выравнивать блоки в памяти (например адреса кратные 2, 4, …), то действия аллокатора останутся точно такими же.

Но, если нам нужно выделять блоки памяти с определенным выравниванием (например выравнивание адресов кратных 2), то здесь действие аллокатора немного меняется. Меняется оно не в плане реализации, а в том, что помимо самих данных равных объему одного байта, мы еще забираем и один дополнительный байт из памяти аллокатора для выравнивания, который не несет никакой смысловой нагрузки. Как раз-таки это и есть та самая возможная минимальная фрагментация памяти внутри линейного аллокатора.

Отлично, теперь самое время поговорить об освобождении памяти. Как уже отмечалось ранее, данный вид аллокоторов не поддерживает выборочное освобождение определенных блоков памяти. То есть, если провести тонкую аналогию с malloc/free, имея указатель, скажем, на 0xFFAA00, мы могли бы освободить этот блок памяти, но вот линейный аллокатор нам этого позволить не может.

Все, что мы можем сделать, это освободить всю занятую память целиком внутри аллокатора и продолжить работать с ним, как с совершенно пустым.

Pool Allocator

Идея блочного аллокатора заключается в том, что он разделяет некоторый большой участок памяти на более мелкие участки одинакового размера. По своей сути он также является очень простым аллокатором, так как, когда запрашивается выделение, он просто возвращает один из свободных участков памяти фиксированного размера, а когда запрашивается освобождение то, он просто сохраняет этот участок памяти для дальнейшего использования. Таким образом, распределение работает очень быстро, а фрагментация все еще очень мала.

Дальше, также, как и с линейным аллокатором, предлагаю рассмотреть все на примере, чтобы детальнее понять, как он работает, поэтому возьмем некоторый блок памяти равный 12 байт и отдадим его в управление аллокатору. Как видно из картинки ниже, мы сохраняем указатель на начало (start) и конец (end) памяти, которой управляет аллокатор, а также список (freeblocks) из адресов свободных блоков в аллокаторе. В качестве средства для хранения данных о том, что блок занят или свободен, можно использовать много средств, например массив из булевых значений, но я именно решил остановиться на выборе односвязного списка, так как он наиболее просто и наглядно характеризует данную концепцию (кстати, сами звенья списка можно хранить в свободных блоках памяти, тем самым убрав дополнительные расходы с памятью).

Если приходит запрос на выделение одного блока памяти, то действия аллокатора очень примитивные. Сначала он проверяет, есть ли звенья в списке свободных блоков, если их там нет, то не трудно догадаться, что память в аллокаторе уже закончилась. Если же там есть хотя бы одно звено, то он просто достает корневое или хвостовое (в данной реализации отдаются хвостовые звенья) звено списка и отдает его адрес пользователю.

Если приходит запрос на выделение нескольких блоков памяти, то аллокатор точно так же по очереди проделывает те же действия, описанные на предыдущем шаге.

Что касается освобождения блока, если приходит запрос на освобождение, то тогда аллокатор просто добавляет этот адрес в один из концов односвязного списка. Стоит отметить такой момент, что в качестве адреса блока для освобождения может прийти, например адрес, несоответствующий адресу памяти аллокатора, например 0xEFAB12, и тогда будет возможна такая ситуация, что мы в дальнейшем отдадим пользователю тот участок памяти, который нам не принадлежит (конечно же, это приведет к undefined behavior или если очень сильно повезет, то просто к краху программы). Для избегания этой возможной проблемы как раз-таки и используются begin и end, которые позволяют проверить, не ошибся ли пользователь адресом во время запроса на операцию освобождения.

Помимо выхода за пределы памяти, которой не управляет аллокатор, есть еще одна возможная проблема. Пользователь может прийти с запросом освободить совершенно любой адрес, находящийся в области памяти аллокатора, но не равный адресу начала какого-либо из блоков, допустим блока с адресом 0xFFAA07. Эта операция, конечно же, приведет к undefined behavior. Если есть необходимость дополнительно проверять, все ли правильно делает пользователь, то есть возможность это отслеживать. Для отслеживания этого существует множество решений, например хранить также адреса и занятых блоков или вообще проверять адрес на кратность размеру блоков в аллокаторе (все зависит от фантазии и от конкертной ситуации, в которой используется аллокатор).

Stack Allocator

На самом деле, это умная эволюция линейного распределителя, которая позволяет управлять памятью, как стеком. Все так же, как и раньше, мы сохраняем указатель вместе с «header» блоком (в дальнейшем будет употребляться, как заголовок) на текущий адрес памяти и перемещаем его вперед для каждого выделения. В отличие от линейного аллокатора, мы также можем переместить его назад, то есть выполнить операцию deallocate, которая линейным аллокатором не поддерживается. Как и прежде, сохраняется принцип пространственной локальности, а фрагментация все еще минимальная.

Предлагаю рассмотреть несколько примеров все с тем же блоком памяти в 14 байт. Как и с линейным аллокатором, мы точно также сохраняем указатели на начало памяти (start) и конец (end), а также указатель на конец используемой памяти (used).

Когда приходит запрос на выделение памяти, помимо выделения некоего ее объема памяти, запрашиваемого пользователем, мы еще дополнительно выделяем заголовок (пользователь с ним никак не будет взаимодействовать), в котором храним сведения о том, сколько было выделено байт (в данном примере размер заголовка составляет 2 байта). Например, если пришел запрос на выделение 2 байт, то состояние аллокатора будет точно таким же, как на рисунке ниже. Важно отметить то, что пользователю будет отдан указатель не на заголовок, а на блок, следующий сразу за заголовком, то есть в данном примере это блок с адресом 0xFFAA02.

Аналогичная ситуация будет и, например с выделением 6 байт.

А вот с освобождением все немного поинтереснее (как уже обсуждалось ранее, выделять и освобождать память мы можем только с использованием алгоритма LIFO). Для начала от указателя, который пользователь просит освободить, нужно отнять размер заголовка, после чего разыменовать значение и уже только после этого сдвинуть указатель used на размер заголовка вместе с размером блока, полученного из заголовка. Здесь так же, как и с блочным аллокатором, возможна ситуация освобождения «рандомных» блоков памяти, которая также приведет к undefined behavior. Дополнять аллокаторы дополнительными проверками или нет – дело каждого. Самое главное — не забывать об этом моменте.

Теперь, разобравшись в основах, самое время освоить что-то более серьезное.

«Примитивный стандартный аллокатор»

Дальше будет представлена реализация аллокатора, который можно будет без проблем использовать с STL. Алгоритм распределения памяти в этом аллокаторе будет схож с алгоритмом, который используется стандартным аллокатором. Хочу сразу отметить, что не претендую на полноту реализации malloc, мною были взяты лишь основные концепции из него c добавлением в некоторых местах своей логики. Все его тонкости и нюансы, конечно же, не были учтены в этой реализации…

В основе алгоритма лежит взаимодействие с «chunks» (дальше будет употреблено, как участок, в данной реализации их размер статичен и должен быть кратен четырем, а также все выделения памяти из памяти аллоктора выравниваются на размер, кратный четырем), о которых дальше и пойдет речь. В качестве примера возьмем участок c размером 16 байт. Внутри себя он будет содержать указатели на начало (start) и конец (end) памяти, указатель на максимальный блок памяти (maxblock) и множество (freeblocks), в котором будут храниться заголовки свободных блоков. Размер заголовка в данной реализации занимает 4 байта, но он может без проблем варьироваться в размере для нужных вам целей. Например, если вы точно знаете, что размер выделяемых блоков памяти будет не больше, чем максимальное числовое значение, которое можно представить в одно или двухбайтной переменной, то можно будет использовать заголовок в размере 1 или 2 байт.

При операции выделения памяти из участка, прежде всего нужно проверить, достаточно ли памяти (в данной реализации, это константная операция, мы просто сравниваем с maxblock заголовком и, если размер аллоцируемой памяти меньше, чем максимальный блок, то значит у нас достаточно памяти для этого выделения). Если памяти достаточно, то мы просто отдаем адрес памяти, следующий за заголовком, как и в стековом аллокаторе, а также удаляем прошлый заголовок из множества свободных блоков и уже только после этого добавляем туда новый заголовок, только что выделенного блока памяти. Важно отметить, что если мы аллоцировали память из максимального блока, то нам нужно будет обновить значение максимального блока.

При последующих выделениях все происходит точно также, как и на предыдущем шаге.

Но вот как только память в участке закончилась, аллокатор берет и просто создает еще один участок того же или большего размера (в данной реализации все участки одинакового размера). Стоит также следить за тем, чтобы размер возможного блока для выделения не превышал размер участка с вычетом размера заголовка.

Дальше уже в новом участке можно без проблем выделять нужные блоки памяти. Выделение памяти будет происходить по точно такому же сценарию, как и в предыдущем участке.

Теперь немного о том, почему именно в данной реализации размер участка должен быть кратен четырем. Ответ очень просто – это делается для простоты реализации и восприятия алгоритма. Так как возможна такая ситуация, что в конце участка может остаться некоторая область памяти, в которой просто на просто не поместится заголовок (пример этого продемонстрирован на следующем рисунке). Чтобы решить эту проблему, можно будет заполнять эту память дополнительным выравниваем, либо делать размер заголовка меньшим или же использовать дополнительные средства для отслеживания этой возможной проблемы, иначе эта память будет потеряна и самая главное, что в дальнейшем потерянная память сможет накапливаться!

Прежде, чем освободить память, нужно определить, в каком участке находится блок (в текущей реализации эта операция с линейной сложностью относительно общего количества участков, если подразумевается, что будет большое количество участков, то ее можно будет сделать константной, добавив в заголовок индекс участка, в котором была выделена память). В последующем операция освобождения идентична со стековым аллокатором, за исключением того, что нужно будет добавить адрес заголовка освобожденного блока во множество свободных блоков, а также обновить maxblock, если размер только что освобожденного блока больше, чем maxblock.

Важно отметить, что в данной реализации, при каждом последующем освобождении памяти происходит попытка дефрагментации в том участке из которого была освобождена память. Дефрагментация нужна для того, чтобы объединять свободные блоки в большие по размеру. Например, в данной ситуации, как на рисунке ниже, мы не сможем выделить 6 байт, пусть даже размер свободной памяти нам и позволяет это сделать, но зато фрагментация говорит нам твердое и решительное «нет»!

Операция дефрагментации очень примитивная. Суть ее заключается в том, что после операции освобождения памяти идет проверка, не свободны ли два соседних блока слева и справа от освобожденного. Если два соседствующих блока свободны, то они объединяются в один единый.

Еще хотелось бы отметить, что данная реализация будет катастрофически ужасно работать с выделением маленьких блоков памяти, например равных 1 байту. В такой ситуации мы получаем +7 лишних байт на выделение всего лишь одно байта памяти из-за того, что размер заголовка равен 4 байтам и еще плюс 3 байта для вырывания адресов, которые должны быть кратны четырем. Этим я хочу сказать, что не стоит слепо использовать какой-либо алгоритм распределения памяти, так как вместо долгожданной оптимизации иногда можно получить только лишь дополнительные затраты.

Думаю, теории будет достаточно и поэтому, как сказал Линус Торвальдс: «Болтовня ничего не стоит. Покажите мне код». Ну что ж, приступаем…

Реализация

Требования к аллокаторам приведены в стадарте С++ в главе "Allocator requirements [allocator.requirements]". Исходя из тех требований самый примитивный интерфейс аллокатора, который может использоваться в STL, должен выглядеть примерно вот так:

template<class T>
class Allocator 
{
    typedef T value_type;
    Allocator(аргументы конструктора);
    template <class T> 
    Allocator(const <T>& other);
    T* allocate(std::size_t count_objects);
    void deallocate(T* ptr, std::size_t count_objects);
};

template<class T, class U>
bool operator==(const Allocator<T>&, const Allocator<U>&);
template<class T, class U>
bool operator!=(const Allocator<T>&, const Allocator<U>&);

Предполагается, что STL контейнеры обращаются к аллокатору не напрямую, а через шаблон std::allocator_traits, который предоставляет значения, такие как:

typedef T* pointer;
typedef const T* const_pointer; 
… 

Отлично, с требованиями разобрались, теперь наконец приступаем к написанию аллокатора. Для начала напишем некоторый интерфейс или адаптер, на самом деле это трудно назвать и тем, и другим, поэтому пусть это будет некая «прослойка», в которой при помощи стратегий мы сможем без проблем менять алгоритм аллоцирования памяти для определенных целей:

// Common interface for interaction with STL
// containers and algorithms. You can manually change
// allocation algorithm with different 'AllocationStrategy'
//
// In this implementation was not implented 'adress' and 'max_size'
// unnecessary functions for.

template<typename T, class AllocationStrategy>
class Allocator
{
    static_assert(!std::is_same_v<T, void>, "Type of the allocator can not be void");
public:
    using value_type = T;

    template<typename U, class AllocStrategy>
    friend class Allocator;
    
    template<typename U>
    struct rebind
    {
        using other = Allocator<U, AllocationStrategy>;
    };
public:
    Allocator() = default;
    
    explicit Allocator(AllocationStrategy& strategy) noexcept
        : m_allocation_strategy(&strategy) {}
    
    Allocator(const Allocator& other) noexcept
        : m_allocation_strategy(other.m_allocation_strategy) {}
    
    template<typename U>
    Allocator(const Allocator<U, AllocationStrategy>& other) noexcept
        : m_allocation_strategy(other.m_allocation_strategy) {}
    
    T* allocate(std::size_t count_objects)
    {
        assert(m_allocation_strategy && "Not initialized allocation strategy");
        return static_cast<T*>(m_allocation_strategy->allocate(count_objects * sizeof(T)));
    }
    
    void deallocate(void* memory_ptr, std::size_t count_objects)
    {
        assert(m_allocation_strategy && "Not initialized allocation strategy");
        m_allocation_strategy->deallocate(memory_ptr, count_objects * sizeof(T));
    }
    
    template<typename U, typename... Args>
    void construct(U* ptr, Args&&... args)
    {
        new (reinterpret_cast<void*>(ptr)) U { std::forward<Args>(args)... };
    }
    
    template<typename U>
    void destroy(U* ptr)
    {
        ptr->~U();
    }
private:
    AllocationStrategy* m_allocation_strategy = nullptr;
};

template<typename T, typename U, class AllocationStrategy>
bool operator==(const Allocator<T, AllocationStrategy>& lhs, const Allocator<U, AllocationStrategy>& rhs)
{
    return lhs.m_allocation_strategy == rhs.m_allocation_strategy;
}

template<typename T, typename U, class AllocationStrategy>
bool operator!=(const Allocator<T, AllocationStrategy>& lhs, const Allocator<U, AllocationStrategy>& rhs)
{
    return !(lhs == rhs);
}

Благодаря стратегии для распределения памяти, мы сможем делать примерно вот так:

template<typename T>
using AllocatorForSmallObjects = Allocator<T, StrategyForSmallObjects>;
template<typename T>
using AllocatorForBigObjects = Allocator<T, StrategyForBigObjects>;

То есть мы можем гибко менять алгоритмы распределения для необходимых целей в той или иной ситуации. Единственное требование к AllocationStrategy — у них должны быть операции allocate и deallocate.

// Strategy for manipulation memory chunks, like
// a primitive malloc allocator.
//
// Warning: if you try to deallocate some random block
// of the memory, most of all it will be an undefined behavior,
// because current implementation doesn't check this possible situation.

template<std::size_t CHUNK_SIZE = 16'384u>
class CustomAllocationStrategy
{
    static_assert(CHUNK_SIZE != 0u, "Chunk size must be more, than zero");
    static_assert(CHUNK_SIZE <= std::numeric_limits<std::uint32_t>::max(),
        "Chunk size must be less or equal max value of the uint32_t");
public:
    void* allocate(std::size_t size)
    {
        assert(size < CHUNK_SIZE && "Incorrect chunk size for future usage");

        if (size == 0u)
        {
            return nullptr;
        }
        
        for (auto& chunk : m_chunks)
        {
            void* allocated_block = chunk.tryReserveBlock(size);
            if (allocated_block) //if the block was not reserved, then memory in the chunk has run out
            {
                return allocated_block;
            }
        }

        m_chunks.push_back(details::Chunk<CHUNK_SIZE>{});
        auto& chunk = m_chunks.back();
        std::uint8_t* allocated_block = chunk.tryReserveBlock(size);
        return allocated_block;
    }

    void deallocate(void* memory_ptr, std::size_t size)
    {
        if ( (!memory_ptr) || (size == 0u) )
        {
            return;
        }

        std::uint8_t* deallocation_ptr = static_cast<std::uint8_t*>(memory_ptr);
        for (auto& chunk : m_chunks)
        {
            if (chunk.isInside(deallocation_ptr))
            {
                chunk.releaseBlock(deallocation_ptr);
            }
        }
    }
private:
    std::deque<details::Chunk<CHUNK_SIZE>> m_chunks{ 1u };
};

Здесь и дальше используются стандартные контейнеры. Согласен, что будет очень много выделений из кучи. Думаю, что для тех, кто будет писать свои аллокаторы, это будет неприемлемо. В качестве альтернативы, конечно же, можно писать свои контейнеры или использовать чужие, заточенные под определенные нужды, но в данной реализации я старался как можно проще преподнести материал, поэтому мой выбор лег именно на стандартные контейнеры.

namespace details
{

    std::size_t getAlignmentPadding(std::size_t not_aligned_address, std::size_t alignment)
    {
        if ( (alignment != 0u) && (not_aligned_address % alignment != 0u) )
        {
            const std::size_t multiplier = (not_aligned_address / alignment) + 1u;
            const std::size_t aligned_address = multiplier * alignment;
            return aligned_address - not_aligned_address;
        }

        return 0u;
    }

    // Current chunk implementation works only with size
    // aligned by 4 bytes, because HEADER_SIZE now also 4 bytes.
    // You can modify it with HEADER_SIZE without problems for your purposes.

    template<std::size_t CHUNK_SIZE>
    class Chunk
    {
        static constexpr std::size_t HEADER_SIZE = 4u;
        static_assert(CHUNK_SIZE % HEADER_SIZE == 0, "CHUNK_SIZE must be multiple of the four");
        static_assert(CHUNK_SIZE > HEADER_SIZE, "CHUNK_SIZE must be more than HEADER_SIZE");
    public:
        Chunk()
        {
            m_blocks.resize(CHUNK_SIZE);
            std::uint32_t* init_header = reinterpret_cast<std::uint32_t*>(m_blocks.data());
            *init_header = CHUNK_SIZE - HEADER_SIZE;
            m_max_block = init_header;
            m_free_blocks.insert(init_header);
        }
        
        bool isInside(const std::uint8_t* address) const noexcept
        {
            const std::uint8_t* start_chunk_address = reinterpret_cast<const std::uint8_t*>(m_blocks.data());
            const std::uint8_t* end_chunk_address = start_chunk_address + CHUNK_SIZE;
            return (start_chunk_address <= address) && (address <= end_chunk_address);
        }
        
        std::uint8_t* tryReserveBlock(std::size_t allocation_size)
        {
            const std::size_t not_aligned_address = reinterpret_cast<std::size_t>(m_max_block) + allocation_size;
            const std::size_t alignment_padding = getAlignmentPadding(not_aligned_address, HEADER_SIZE);
            const std::uint32_t allocation_size_with_alignment = static_cast<std::uint32_t>(allocation_size + alignment_padding);
            if ( (!m_max_block) || (allocation_size_with_alignment > *m_max_block) ) // Check on enaught memory for allocation
            {
                return nullptr;
            }
            
            // Find min available by size memory block
            const auto min_it = std::min_element(m_free_blocks.cbegin(), m_free_blocks.cend(), [allocation_size_with_alignment] (const std::uint32_t* lhs, const std::uint32_t* rhs)
            {
                if (*rhs < allocation_size_with_alignment)
                {
                    return true;
                }
                
                return (*lhs < *rhs) && (*lhs >= allocation_size_with_alignment);
            });
            
            assert(min_it != m_free_blocks.cend() && "Internal logic error with reserve block, something wrong in implementation...");
            assert(**min_it >= allocation_size_with_alignment && "Internal logic error with reserve block, something wrong in implementation...");
            
            std::uint32_t* header_address = *min_it;
            std::uint32_t* new_header_address =
                reinterpret_cast<std::uint32_t*>(reinterpret_cast<std::uint8_t*>(header_address) + HEADER_SIZE + allocation_size_with_alignment);
            if (m_free_blocks.find(new_header_address) == m_free_blocks.cend()) // check if there is free memory in the current block
            {
                const std::uint32_t old_block_size = *header_address;
                const std::uint32_t difference = old_block_size - HEADER_SIZE;
                if (difference >= allocation_size_with_alignment) // check if there is enough space for another block
                {
                    const std::uint32_t new_block_size = difference - allocation_size_with_alignment;
                    *new_header_address = new_block_size;
                    m_free_blocks.insert(new_header_address);
                }
            }
            
            m_free_blocks.erase(header_address);
            *header_address = static_cast<std::uint32_t>(allocation_size);
            if (header_address == m_max_block) // if the maximum block were changed, then need to find the maximum block again
            {
                // Find max block by size
                const auto max_it = std::max_element(m_free_blocks.cbegin(), m_free_blocks.cend(), [] (const std::uint32_t* lhs, const std::uint32_t* rhs)
                {
                    return (*lhs) < (*rhs);
                });
                
                // If there are no free blocks, therefore the memory in this chunk is over
                m_max_block = (max_it != m_free_blocks.cend()) ? (*max_it) : (nullptr);
            }

            return reinterpret_cast<std::uint8_t*>(header_address) + HEADER_SIZE;
        }
        
        void releaseBlock(std::uint8_t* block_ptr)
        {
            std::uint8_t* header_address = block_ptr - HEADER_SIZE;
            const std::uint32_t size_relized_block = *header_address;
            if ( (!m_max_block) || (size_relized_block > *m_max_block) ) // if the relized block is greater than the maximum, then need to replace it
            {
                m_max_block = reinterpret_cast<std::uint32_t*>(header_address);
            }
                
            m_free_blocks.insert(reinterpret_cast<std::uint32_t*>(header_address));
            auto forward_it = m_free_blocks.find(reinterpret_cast<std::uint32_t*>(header_address));
            auto backward_it = tryDefragment(forward_it, m_free_blocks.end());
            tryDefragment(std::make_reverse_iterator(backward_it), m_free_blocks.rend());
        }
    private:
        template<typename DstIterator, typename SrcIterator>
        constexpr DstIterator getIterator(SrcIterator it) const
        {
            using iterator = std::set<std::uint32_t*>::iterator;
            using reverse_iterator = std::set<std::uint32_t*>::reverse_iterator;
            if constexpr ( (std::is_same_v<SrcIterator, iterator>) && (std::is_same_v<DstIterator, reverse_iterator>) )
            {
                return std::make_reverse_iterator(it);
            }
            else if constexpr ( (std::is_same_v<SrcIterator, reverse_iterator>) && (std::is_same_v<DstIterator, iterator>) )
            {
                return it.base();
            }
            else
            {
                return it;
            }
        }
        
        template<typename Iterator>
        Iterator tryDefragment(Iterator start_it, Iterator end_it)
        {
            // primitive defragmentation algorithm - connects two neighboring
            // free blocks into one with linear complexity
   
            auto current_it = start_it++;
            auto next_it = start_it;
            std::uint32_t* current_header_address = *current_it;
            if ( (current_it != end_it) && (next_it != end_it) )
            {
                std::uint32_t* next_header_address = *next_it;
                const std::uint32_t current_block_size = *current_header_address;
                const std::uint32_t* available_current_block_address =
                    reinterpret_cast<std::uint32_t*>(reinterpret_cast<std::uint8_t*>(current_header_address) + HEADER_SIZE + current_block_size);
                if (available_current_block_address == next_header_address)
                {
                    const std::uint32_t next_block_size = *next_header_address;
                    const std::uint32_t new_current_block_size = current_block_size + HEADER_SIZE + next_block_size;
                    *current_header_address = new_current_block_size;
                    if (new_current_block_size > *m_max_block)
                    {
                        m_max_block = reinterpret_cast<std::uint32_t*>(current_header_address);
                    }
                            
                    auto delete_it = getIterator<std::set<std::uint32_t*>::iterator>(next_it);
                    return getIterator<Iterator>(m_free_blocks.erase(delete_it));
                }
            }
            
            return current_it;
        }
    public:
        std::vector<std::uint8_t*> m_blocks;
        std::set<std::uint32_t*> m_free_blocks;
        std::uint32_t* m_max_block;
    };

}

Теперь немного о том, как можно украсить использование аллокаторов вместе со стандартными контейнерами:

template<typename T, std::size_t CHUNK_SIZE = 16'384u>
using CustomAllocator = Allocator<T, CustomAllocationStrategy<CHUNK_SIZE>>;

template<typename T>
using CustomAllocatorWithStackChunks = Allocator<T, CustomAllocationStrategy<1'024u>>;

template<typename T>
using CustomAllocatorWithHeapChunks = Allocator<T, CustomAllocationStrategy<16'384u>>;

template<typename T>
using custom_vector = std::vector<T, CustomAllocator<T>>;

template<typename T>
using custom_list = std::list<T, CustomAllocator<T>>;

template<typename T>
using custom_set = std::set<T, std::less<T>, CustomAllocator<T>>;

template<typename T>
using custom_unordered_set = std::unordered_set<T, std::hash<T>, std::equal_to<T>, CustomAllocator<T>>;

template<typename K, typename V>
using custom_map = std::map<K, V, std::less<K>, CustomAllocator<std::pair<const K, V>>>;

template<typename K, typename V>
using custom_unordered_map = std::unordered_map<K, std::hash<K>, std::equal_to<K>, CustomAllocator<std::pair<const K, V>>>;

using custom_string = std::basic_string<char, std::char_traits<char>, CustomAllocator<char>>;

Можно также использовать аллокаторы и с умными указателями, но для этого придется написать небольшую прослойку:

template<typename T>
using custom_unique_ptr = std::unique_ptr<T, std::function<void(T*)>>;

template<class Allocator, typename T = typename Allocator::value_type, typename... Args>
custom_unique_ptr<T> make_custom_unique(Allocator allocator, Args&&... args)
{
    const auto custom_deleter = [allocator](T* ptr) mutable
    {
        allocator.destroy(ptr);
        allocator.deallocate(ptr, 1u);
    };
        
    void* memory_block = allocator.allocate(1u);
    if (memory_block)
    {
        T* object_block = static_cast<T*>(memory_block);
        allocator.construct(object_block, std::forward<Args>(args)...);
        return custom_unique_ptr<T>{ object_block, custom_deleter };
    }

    return nullptr;
}

Ну и теперь, наконец, пример использования всего этого:

int main(int argc, char** argv)
{
    CustomAllocationStrategy allocation_area{};

    CustomAllocator<int> custom_int_allocator{ allocation_area };
    custom_vector<int> vector{ custom_int_allocator };
    for (int i = 0u; i < 100; ++i)
    {
        vector.push_back(i);
        std::cout << vector.at(i) << " ";
    }
    
    vector.resize(16u);
    for (int val : vector)
    {
        std::cout << val << " ";
    }

CustomAllocator<int> custom_int_allocator_copy = vector.get_allocator();
    custom_unique_ptr<int> ptr1 = make_custom_unique<CustomAllocator<int>>(custom_int_allocator_copy, 100);
    custom_unique_ptr<int> ptr2 = make_custom_unique<CustomAllocator<int>>(custom_int_allocator_copy, 500);
    custom_unique_ptr<int> ptr3 = make_custom_unique<CustomAllocator<int>>(custom_int_allocator_copy, 1000);
    custom_unique_ptr<int> ptr4 = make_custom_unique<CustomAllocator<int>>(custom_int_allocator_copy, 1500);
    std::cout << *ptr1 << " " << *ptr2 << " " << *ptr3 << " " << *ptr4 << " ";
    
    CustomAllocator<float> custom_float_allocator { custom_int_allocator };
    custom_list<float> list{ { 10.0f, 11.0f, 12.0f, 13.0f, 14.0f, 15.0f }, custom_float_allocator };
    for (float val : list)
    {
        std::cout << val << " ";
    }
    
    CustomAllocator<std::pair<double, double>> custom_pair_allocator{ allocation_area };
    custom_map<double, double> map{ { { 1.0, 100.0 }, { 2.0, 200.0 } }, custom_pair_allocator };
    for (const auto& it : map)
    {
        std::cout << "{" << it.first << " : " << it.second << "} ";
    }
    
    CustomAllocator<double> custom_double_allocator{ allocation_area };
    custom_set<double> set{ { 1000.0, 2000.0, 3000.0 }, custom_double_allocator };
    for (double val : set)
    {
        std::cout << val << " ";
    }

    CustomAllocator<char> custom_char_allocator{ allocation_area };
    custom_string string1{ "First allocated string without SBO ", custom_char_allocator };
    custom_string string2{ "Second allocated string without SBO ", custom_char_allocator };
    custom_string string3{ "Third allocated string without SBO ", custom_char_allocator };
    custom_string result_string = string1 + string2 + string3;
    std::cout << result_string;
    
    return EXIT_SUCCESS;
}

Хотелось бы заострить внимание на том, что данная реализация является самой примитивной, но она может быть без проблем расширена в ту сторону, которая вам необходима, поэтому все в ваших руках!

Заключение

Спасибо за внимание, очень надеюсь, что данная статья оказалась кому-то полезной. Также желаю всем успехов в тесном взаимодействии с памятью, и самое главное, не забывать очень важные слова Дональда Кнута: «Преждевременная оптимизация — корень всех зол».

Ссылка на репозиторий с полной реализацией аллокатора.

Используемые источники

1. habr.com/ru/post/274827
2. github.com/mtrebi/memory-allocators

Let's block ads! (Why?)

[Из песочницы] Объективность рейтинга публикации

Здравствуйте, уважаемые хабровчане. В данном посте описано моё наблюдение касательно корпоративного блока и субъективное мнение об объективности рейтинга статей на хабре. Статья — под катом.

Дисклеймер: данный пост не несет цели кого-либо обвинить, все это — субъективные мысли автора.
Пользуясь Хабром более года, лишь в последнее время стал замечать особенность: некоторые статьи компаний имеют высокий рейтинг публикаций, при том, что они не имеют ни активного обсуждения в комментариях, ни большого количества просмотров.

Для сравнения, вот некоторые публикации вне корпоративного блога, которые имеют сравнимый рейтинг. Касательно объективности такого сравнения — чуть ниже:

Конечно, нельзя обвинять никого в накрутке, потому что это вполне может быть как и крайне хорошая статья в блоге компании, так и спорная статья, опубликованная независимым автором, соответственно ни рейтинг статьи, ни количество просмотров — не показатель. Однако слишком часто я замечаю картину следующего характера: вышла статья в блоге компании полчаса назад, её просмотрело полтысячи человек, которые массово поставили ей суммарно 15-20 плюсов, и слишком редко я такое наблюдаю в статьях независимых авторов.

Естественно, справедливо заметить: «ну даже если кто-то и накручивает рейтинг — что с того?». Ответ иным вопросом: когда вы видите статью с высоким рейтингом — это вызывает у вас интерес, желание открыть, прочесть её, она вызывает бОльший интерес, нежели статья с околонулевым рейтингом?

В большинстве случаев статьи в блоге компании содержат рекламу, и высокий рейтинг публикации становится одним из факторов релевантности маркетинга компании на весьма авторитетной площадке с крайне высоким качеством аудитории — ведь большинство читателей хабра имеют высокую покупательную способность, являются взрослыми и состоятельными людьми.

В это же время, на мой взгляд, рейтинг статьи должен отображать лишь актуальность и качественность самой статьи — но не служить инструментом продвижения и пиара каких-либо компаний. Если статья актуальна, качественна и интересна — она будет иметь высокий рейтинг и сама по себе, и реклама в такой статье будет лишь подтверждением того, что компания, опубликовавшая данный пост поощряет создание интересного контента своими работниками, и что сами сотрудники компании — образованные люди, с которыми приятно работать и которые могут предоставлять качественные услуги клиентам.

Когда написание статей в блогах компаний ставится на конвейер, а их главной целью становится не создание качественного контента, интересного пользователям, а лишь реклама услуг компании — мне кажется, в этот момент сам Хабр теряет свою актуальность и независимость.

В памятке для пишущих статьи есть пункт, гласящий, что жалобные статьи это плохо. Однако мне неизвестно иного способа донести недовольство ситуацией, ведь любая критика — это жалоба на то, что не устраивает пользователя информационного ресурса, зрителя фильма, читателя книги.

Подводя итог, хочу отметить, что я ни в коем случае не обвиняю компании в накрутке рейтинга, а администрацию Хабра — в его необъективности, ибо просто не имею никаких объективных аргументов. Только хочу задать вопрос, вызывают ли у вас доверие ситуации, когда статья, просмотренная 160-ю людьми, имеет рейтинг +18?

Let's block ads! (Why?)

[Из песочницы] МК-61: история, эмуляция, устройство

Расцвет эпохи программируемых калькуляторов в нашей стране пришёлся на середину 80-х годов. Потом на смену относительно сытым и благополучным временам пришла эпоха бандитского капитализма, когда стране стало не до выпуска своей высокотехнологичной продукции бытового назначения, вот уже сменились поколения, но ностальгия по тем временам, когда мы бессонными ночами пытались сократить код программы хотя бы на пару байтов, чтобы уместить задуманную функцию, выискивали всё новые и новые недокументированные возможности, придумывая способы, как их можно использовать на практике, сочиняли целые циклы рассказов в качестве фона для наших игровых программ, не даёт забыть свой МК-61 со 105 байтами программной памяти. Поэтому хочу написать заметку о том, что собой представляли и как работали эти самые программируемые калькуляторы. Даже если эта тема сегодня периодически и поднимается, то не настолько часто, чтобы приесться уважаемому читателю, так что надеюсь поведать что-то новое.

Немного истории

Для начала небольшой экскурс в историю. Программируемый калькулятор отличается от инженерного возможностью задать пользовательскую программу вычислений, имеет увеличенную память и набор операций для управления ходом исполнения программы, т. е. по сути является примитивным портативным компьютером. Отечественные программируемые калькуляторы (ПМК) принято делить на поколения. Первый массовый советский карманный ПМК, получивший обозначение Б3-21, увидел свет в 1977 году, он имел 60 шагов программной памяти, два операционных регистра X и Y, семь регистров памяти, а также двунаправленный кольцевой стек на шесть чисел (объединённый с X, который выводился на индикатор). Вычисления на нём производились в формате обратной (постфиксной) бесскобочной записи, т. е. сперва в операционный стек помещались операнды, затем над ними производилась операция, — это позволяло значительно упростить как сам калькулятор, так иногда и работу с ним. На базе этого ПМК строилось их первое поколение, к нему относятся, например, настольные варианты МК-46 и МК-64. Несмотря на очевидные недостатки, прежде всего заоблачную цену (350 рублей на момент появления в продаже), появление первых ПМК значительно упростило жизнь людям, имеющим дело со сложными вычислениями.

На смену им пришли «ПМК расширяющегося ряда», про них и пойдёт речь в этой статье. Это поколение в 1980 году начал калькулятор Б3-34, он получил новый процессор из серии К145ИК13 (на его базе также создавались и некоторые инженерные калькуляторы). Он по-прежнему работал в обратной бесскобочной нотации, но зато у него появилось место под 98 шагов программы, 14 регистров памяти и стек из 4 ячеек (плюс дополнительный регистр предыдущего результата), была добавлена косвенная адресация и циклы со счётчиком. Этот ПМК содержит два упомянутых процессора с разной прошивкой: один — как управляющее устройство, другой — как математический сопроцессор. Вместе с двумя микросхемами памяти К145ИР2 они соединены однобитной шиной (магистралью) в кольцо, получая сигналы синхронизации от тактового генератора К145ГФ3.

Наконец, в 1984 году был выпущен МК-61. Получив корпус калькулятора из семейства Б3-34 — МК-54, он получил дополнительный, третий процессор — К745ИК1306. Таким образом у нового устройства появились дополнительные функции (модуль, целая и дробная часть, знак числа и другое), семь дополнительных шагов программной памяти — теперь их стало 105, и ещё один регистр. Стоил он 85 рублей — цена внушительная, но при необходимости подъёмная. Именно эта машинка стала самым массовым и популярным ПМК в нашей стране. В следующем году был выпущен МК-61 с энергонезависимой памятью (ППЗУ) объёмом 512 байтов и возможностью подключения блоков расширения памяти с прошитыми в них библиотеками программ (выпускались централизованно) — МК-52.

Следующее поколение представлено микрокомпьютером МК-85 и его «сородичами». С одной стороны это был качественный скачок вперёд, с другой — это были калькуляторы со встроенным интерпретатором морально устаревшего и даже не русифицированного языка BASIC и 16-битным процессором с системой команд компьютеров американской фирмы DEC. С развалом страны и их производство сошло на нет, на этом история отечественных программируемых калькуляторов заканчивается…

Значимость и продолжение истории

Но семейство Б3-34 прочно закрепилось в быту советского человека. До массового распространения персональных компьютеров оставалось ждать пару десятилетий, да и счастливчикам, ставшим обладателями такового ещё тогда, в карман всё равно его было не положить. А ПМК были относительно доступны и практичны, поэтому и обрели заслуженное уважение наших людей. Я бы даже назвал народную любовь к ПМК социально-культурным явлением. Пользовались этими приборами, казалось бы, сугубо инженерного назначения, все категории граждан: от школьников младших классов до пенсионеров преклонных лет, мужчины и женщины самых разнообразных профессий, со всех концов нашей страны — от Западной Украины до Чукотки и от Кольского полуострова до Средней Азии. Весьма полезными ПМК были и для студентов (прежде всего инженерных специальностей) с интеллектом выше среднего, но поскольку дефицит таковых начал наблюдаться уже тогда, основным контингентом пользователей было всё же взрослое население.

Трудно найти сферу человеческой деятельности, где не был применён наш микрокалькулятор. Нужно подсчитать параметры статистического ряда или определить рентабельность производства? Рассчитать параметры электрической цепи, вычислить молярную массу вещества, найти радиус чёрной дыры? Легко. Смоделировать манёвры боевого самолёта, рассчитать курс морского судна или сориентировать орбитальный корабль? Пожалуйста. Известно, например, что МК-52 реально использовался штурманами военно-морского флота, а также, в качестве запасного вычислительного устройства, космонавтами. Выбрать класс трактора или оценить параметры почвы, определить генетическое расстояние между популяциями, рассчитать пропорции в кулинарии, дозу или концентрацию лекарства, сгенерировать узор для вязания? Всё есть. Увлекаетесь нумерологией, биоритмами и прочей лженаукой? Найдутся и для вас программки.

А игры, которые создавались сотнями и целыми сериями с сюжетом, — это вообще отдельная тема. Было всё: от крестиков-ноликов и мини-шашек до симуляций исторических сражений и экономики государства. Были изданы десятки книг, сборников программ, рецептов программирования. В популярнейших журналах, издававшихся многомиллионными тиражами, таких как «Наука и жизнь», «Техника — молодёжи» и др., регулярно печатались рубрики, посвящённые ПМК. Отдельно очень активно шло изучение недокументированных возможностей калькуляторов этой серии, особенностей реализованных функций и т. п., получившее название «еггогология» — от слова, которым обозначалась ошибка при вычислениях, — «ЕГГОГ». Рассматривались также способы аппаратной модификации устройств.

Сегодня об этой занятной науке можно прочитать лишь в отсканированных журналах, например в библиотеке сайта Сергея Тарасова, посвящённого ПМК. Очень рекомендую тем, кто желает погрузиться в атмосферу тех лет. А на сайте Евгения Века собрано более 250 авторских игровых программ — подборка даёт хорошее представление об игровом движении калькуляторщиков и о самом явлении.

Хотя с развалом страны и прекращением выпуска новых моделей калькуляторов интерес к теме в народе стал резко падать, народные умельцы всё же не сидели без дела. В 2003 году программист Евгений Троицкий разработал симулятор отечественных калькуляторов «Калькуляторы 3000» — арифметических, инженерных и программируемых — наверное, единственный в своём роде с таким охватом и точностью симуляции. А «в железе» на это всё можно посмотреть на сайте музея вычислительной техники Сергея Фролова.

Писались статьи, сканировались печатные материалы, принимались и другие попытки воссоздать калькуляторы программно, переводилась на иностранные языки документация. Причём не только русские люди не дают нашим калькуляторам бесследно раствориться в прошлом. Вот, например, очень примечательные случаи: француз Гийом сравнивает быстродействие МК-61 и МК-52 и пишет транслятор BASIC-подобного языка в код ПМК, голландец Альфред исследует недокументированные особенности МК-61 и возможности «синтетического программирования» калькулятора, а канадец Виктор тестирует и сравнивает МК-61 с другими калькуляторами из своей коллекции.

Кто-то даже пытается заработать на приятных воспоминаниях. Так, новосибирская фирма «Семико» собрала из китайских запчастей пару калькуляторов, назвав их в честь отечественных МК-61 и МК-52 и снабдив похожим языком. Понятно, что дальше продвижения на Интернет-помойках вроде Википедии дело не пошло, и рынок ожидаемо проигнорировал это начинание.

И вот в 2012 году инженер из США Феликс Лазарев, вооружившись профессиональным микроскопом, смог при участии Евгения Троицкого и других энтузиастов проанализировать и восстановить содержимое ПЗУ микросхем процессоров МК-61. Так были созданы первые эмуляторы калькуляторов серии Б3-34 (за исключением МК-52, у которого не была отсканирована микросхема, управляющая энергонезависимой памятью).

Вскоре с использованием восстановленного кода был написан эмулятор МК-61 на JavaScript. Сегодня это, по всей видимости, наиболее функциональный и удобный эмулятор из всех. Не требуя скачивания и установки, он позволяет работать как с самим МК-61, так и с калькуляторами-аналогами Б3-34 (без третьего процессора), а также с такими устройствами, как арифмометр «Феликс-М», логарифмическая линейка «НЛ-10М» и русские счёты. Во время работы калькулятора на экране показывается содержимое всех регистров памяти, операционного стека, адресов возврата из подпрограмм и счётчика команд в режиме реального времени. Имеется возможность скопировать и ввести сохранённое состояние или поставить исполнение на паузу. Важной функцией является возможность ввести и прочитать код программы, используя общепринятые мнемоники команд в различных вариантах, т. е. теперь можно просто скопировать код программы, вставить в эмулятор и запустить, не вводя его вручную.

Работа на калькуляторе

Думаю, многим, кого заинтересовала эта тема, захочется опробовать на практике, «на ощупь» этот самый калькулятор. Так что давайте теперь посмотрим, как собственно работать на этих машинках.

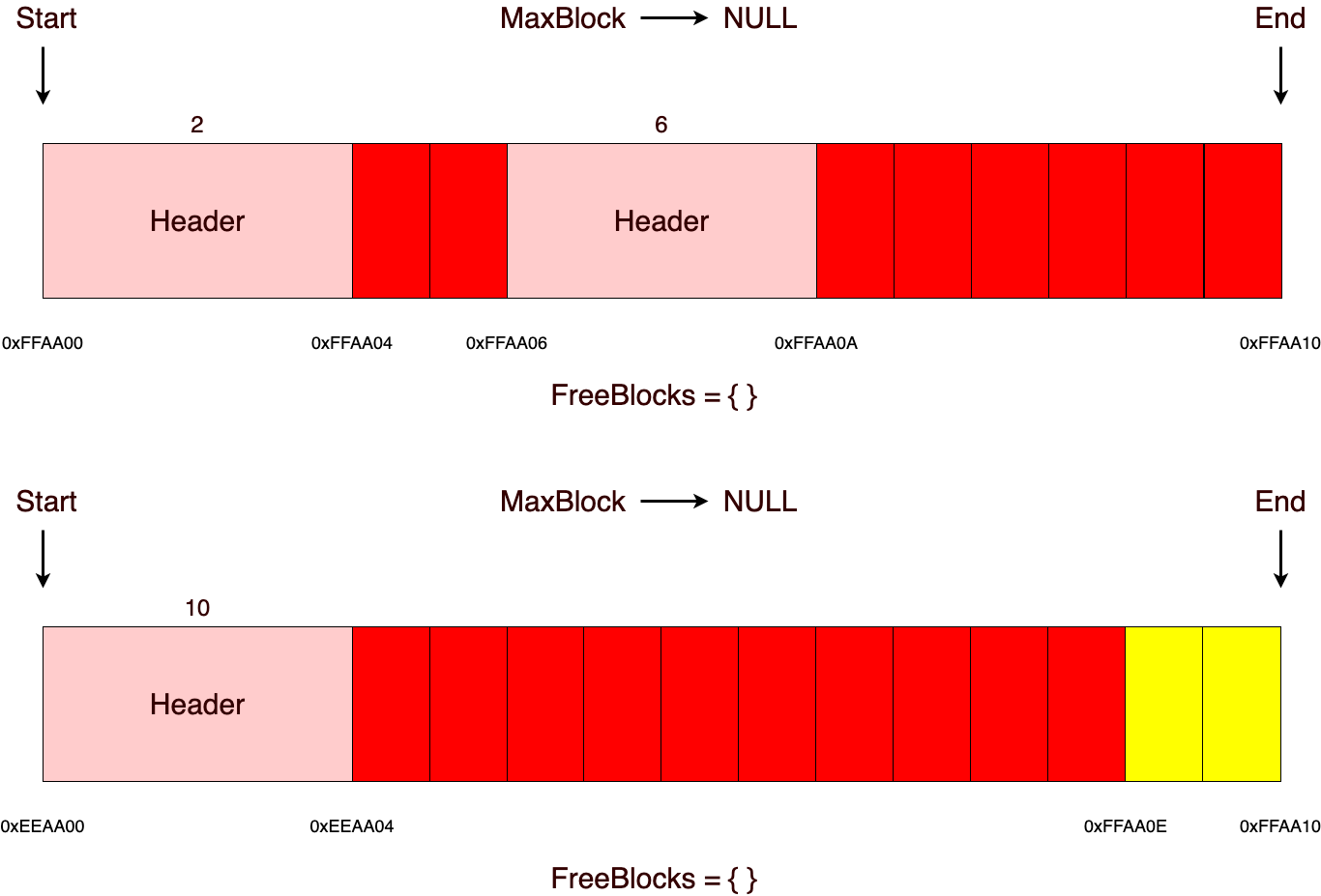
Впервые добравшись до МК-61, человек, знакомый с традиционными арифметическими и инженерными калькуляторами, обычно задаётся вопросом: где здесь кнопка «=» или скобки? Попробуем разобраться. Итак, для начала калькулятор нужно включить. В верхней его части находится индикатор, на котором отображается число, с которым в данный момент работает калькулятор. Он также работает и с другими числами, расположенными в ячейках памяти, называемых регистрами, но обычно результат вводится и выводится на индикатор, значение которого также находится в регистре, обозначаемом X. Слева под индикатором находится переключатель, подписанный справа «Вкл», — включаем, на индикаторе загорится «0». Число набирается традиционно, при помощи цифровых кнопок. Можно также ввести дробное число посредством кнопки десятичной запятой (справа от кнопки «0»), поменять его знак («/−/») и ввести порядок («ВП»). Например, нужно ввести число −0,00000123 — для этого последовательно нажимаем: «[1] [2] [3] /−/ ВП [8] /−/».

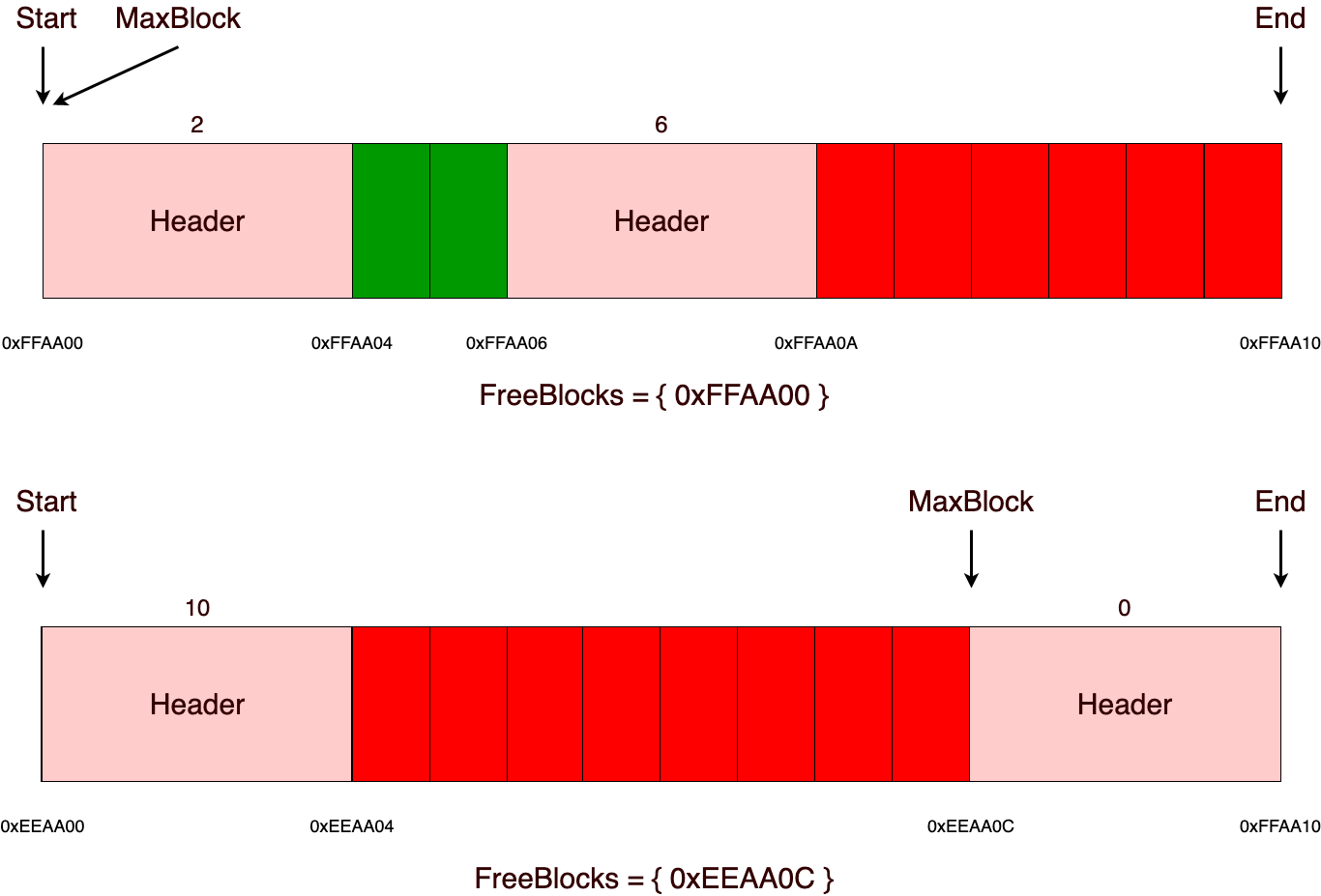
Как же тут выполнять арифметические операции? Чтобы понять это, необходимо ознакомиться с таким понятием, как операционный стек. Стек нашего калькулятора — это просто четыре регистра, связанные между собой порядком помещения и извлечения из них чисел. Он подобен стопке, колоде карт: верхняя карта (в нашем случае число) лежит в регистре X и отображается на индикаторе. Когда мы кладём число в эту стопку, остальные числа оказываются глубже (под ним), а оно перед нами, на индикаторе. В нашем распоряжении находятся четыре регистра стека (и один дополнительный, в него помещается результат предыдущей операции), обозначаемые буквами X, Y, Z, T (и X1), мы можем производить с ним определённые операции. Вводимое с клавиатуры число оказывается в регистре X. Его можно поднять (скопировать) в следующий за ним регистр Y, при этом содержимое Y переместится в Z, содержимое Z — в T (предыдущее значение T сотрётся). Стек можно вращать, при этом X перемещается в T, T — в Z и т. д. Подъём или спуск значений происходит и при выполнении некоторых действий.

Тут дело в том, что калькулятор, как уже было сказано ранее, принимает выражения в бесскобочной постфиксной нотации, т. е. не в традиционной форме «a + b =», а в форме «a b +», т. е. сначала вводятся числа, после производится операция. А вводятся числа как раз в этот самый стек. Введя число в регистр X, его нужно поднять в Y, для этого используется кнопка [В↑]. После этого можно начинать вводить следующее число, предыдущее значение X при этом сотрётся.

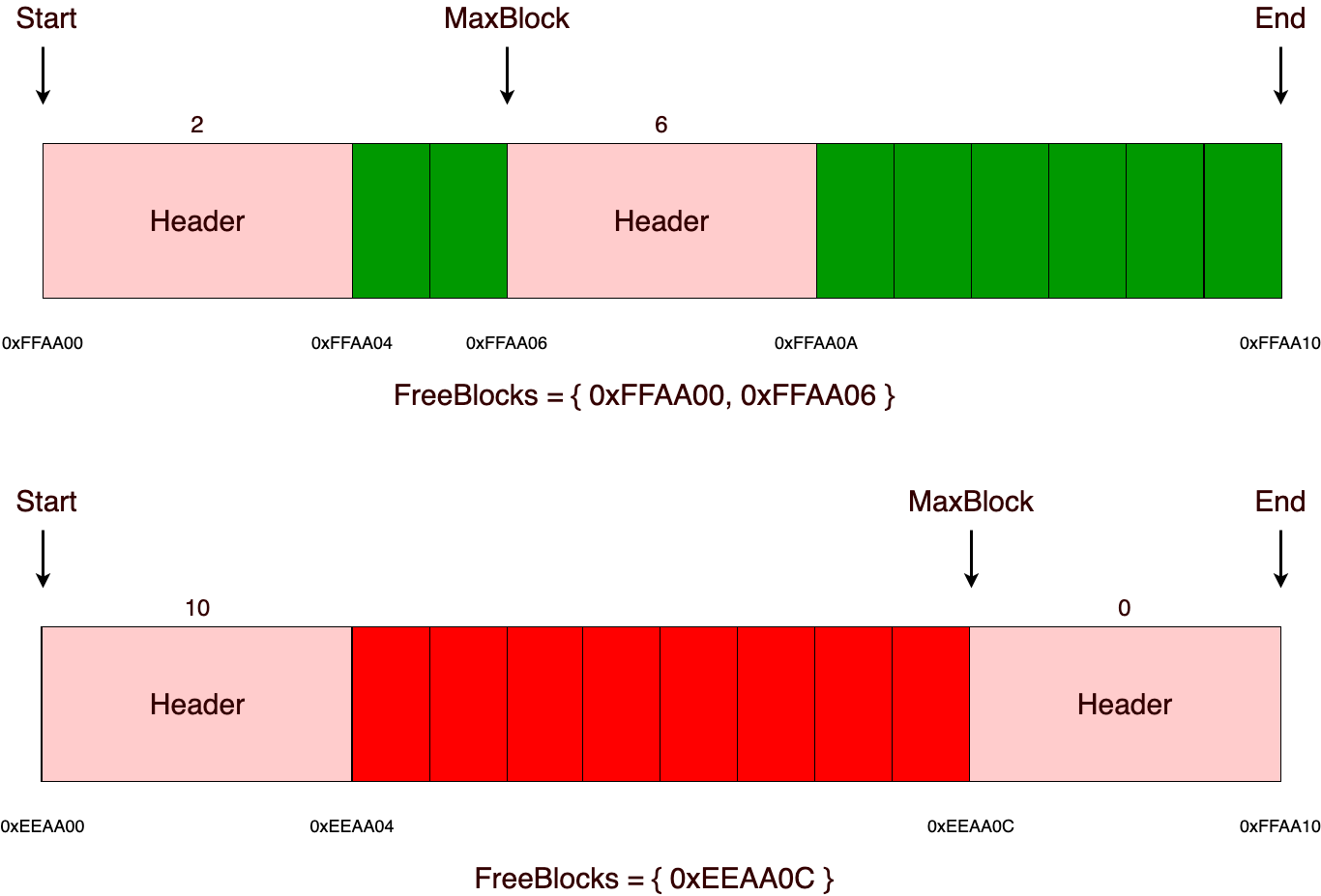
Операции над числами делятся на двухместные (с двумя аргументами: сложение, вычитание, возведение в степень и т. д.) и одноместные (над одним числом: корень, тригонометрия, логарифмы и т. д.). Двухместные операции производятся над регистрами X и Y. Для примера сложим два числа: «[1] [В↑] [2] [+]». Здесь в X вводится число 1, поднимается в Y, в X вводится число 2, после чего Y и X складываются, результат — на индикаторе (в X). При этом значения стека спускаются: T обнуляется, предыдущее значение T перемещается в Z, Z — в Y, в X1 — предыдущее значение X (т. е. 2). В случае с вычитанием выполняется операция $\$inline\$X\; =\; Y\; -\; X\$inline\$$ (аналогично с делением). Для доступа к функциям, обозначения которых нанесены над кнопками, используются кнопки [F] и [K] соответственно цвету, которым написано обозначение функции. Например, для вычисления натурального логарифма числа нужно нажать «[F] [2]» (над кнопкой «2» находится обозначение «ln»).

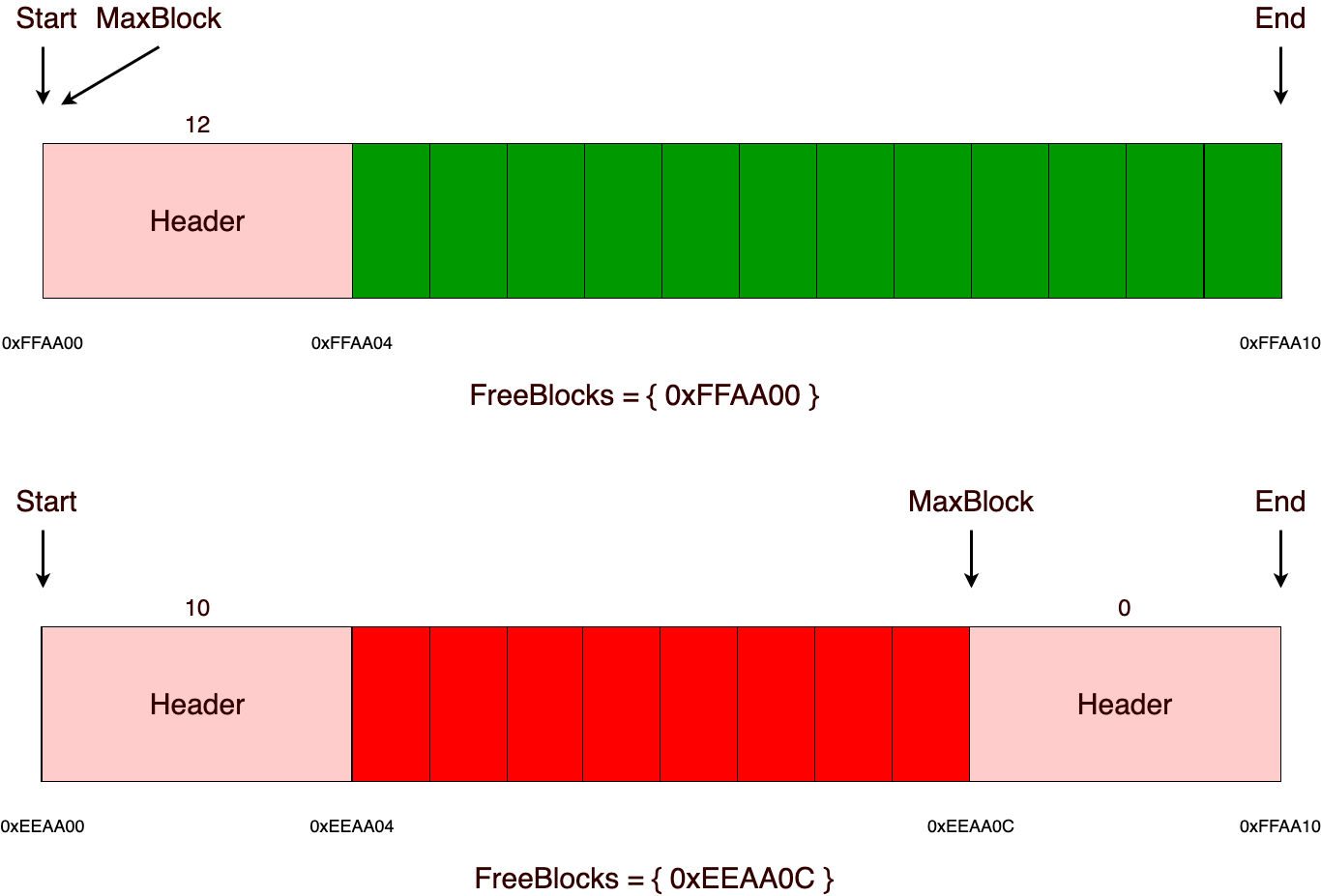
В качестве основной памяти в МК-61 используется 15 регистров общего назначения. Они обозначаются цифрами от 0 до 9 и буквами от A до E (10—15). Для помещения числа в один из регистров используется кнопка «X→П», после нажатия которой нужно нажать соответствующую номеру регистра кнопку на цифровой клавиатуре или кнопку, подписанную нужной буквой снизу/справа от неё. Аналогичным образом число извлекается из регистра посредством кнопки «П→X». При работе на калькуляторе для хранения промежуточных данных зачастую используется стек. При этом необходимо следить, чтобы сохранённое значение не было стёрто в процессе вычислений. В МК-61 существует также косвенная адресация регистров. Так, например, если поместить в регистр №7 число 8, то при помощи последовательного нажатия «[K] [П→X] [7]» на индикаторе появится содержимое регистра №8. Здесь необходимо отметить, что при косвенном обращении через регистры 0—3 ихнее значение предварительно уменьшается на единицу, а через 4—6 — увеличивается. Т. е. если в Р4 было 5, то «[K] [П→X] [4]» выдаст число из Р6.

Теперь посмотрим, как вводятся и исполняются программы. Для запуска режима ввода программы необходимо нажать последовательность кнопок «[F] [ВП]» («ПРГ»). Далее вводится программа, аналогично тому, как производятся вычисления в ручном режиме. В правой части индикатора отображается счётчик команд, текущее его значение показывает адрес, по которому будет размещена вводимая инструкция (шаг программы). Максимальная длина программы — 105 шагов. При вводе программы на индикаторе отображаются три последних (предшествующих указываемому адресу) кода инструкции.

Напишем для примера программу, которая умножит вводимое число на 3, прибавит к нему 4 и возведёт полученное значение в квадрат. Для этого последовательно нажимаем: «[В↑] [3] [×] [4] [+] [F] [×] [С/П]». В результате в программной памяти окажется программа: «↑ 3 × 4 + x² С/П». При оформлении кода программы в текстовом виде указывается не непосредственно клавиша, которую необходимо нажать, а инструкция, которая будет выполнена: в нашем случае — не «F ×», а «x²». Команда «С/П» (стоп/пуск) останавливает выполнение программы.

Теперь выходим из режима программирования нажатием «[F] /−/» («АВТ»). Для запуска программы обнуляем счётчик шагов кнопкой «В/О» (возврат/очистка), вводим начальные данные, например, 5. Запускаем программу — «С/П». После выполнения на индикаторе 361.

Примеры программ

Рассмотрим пример программы, выполняющей реальные вычисления. Этот код вычисляет дату Пасхи по введённому номеру года:

П2      1       9       ПП      86      П3      ИП2     4       ПП      86
П4      ИП2     7       ПП      86      П5      1       9       ИП3     *
1       5       +       3       0       ПП      86      П6      2       ИП4
*       4       ИП5     *       +       6       ИП6     *       +       6
+       7       ПП      86      ИП6     +       П1      3       П4      ИП2
1       -       2       10^x    /       [x]     ^       ^       4       /
[x]     -       2       0       +       ИП1     +       П3      3       1
-       x>=0    76      П3      КИП4    ИП3     3       0       -       x>=0
83      П3      КИП4    ИП3     ИП4     С/П     П0      <->     П1      <->
/       [x]     ИП0     *       ИП1     -       /-/     В/О

Чтобы не вводить его вручную, как на реальном устройстве, достаточно просто вставить его в эмуляторе в окошко «Код программы» и нажать кнопку «Ввести в память». Вводим на клавиатуре номер года, нажимаем «С/П» для запуска (если счётчик команд не обнулён, то обнуляем его, нажав перед запуском «В/О»). Примерно через 14 секунд получим результат: на индикаторе (в регистре X) будет номер месяца, в регистре Y — число месяца; нажимаем «⟷», чтобы обменять значения X и Y и увидеть номер дня.

Или вот такая программа, которая переводит числа в троичную симметричную систему счисления:

ЗН      П2      Вx      |x|     П0      0       П3      П4      1       П5
ИП0     /-/     x<0     80      ИП0     ^       ^       3       /       [x]
П0      3       *       -       П1      ИП3     x#0     54      ИП1     x=0
38      ИП2     ПП      88      0       П3      БП      10      ИП1     1
-       x=0     49      ИП2     /-/     ПП      88      БП      10      0
ПП      88      БП      10      ИП1     x=0     62      0       ПП      88
БП      10      ИП1     1       -       x=0     72      ИП2     ПП      88
БП      10      ИП2     /-/     ПП      88      1       П3      БП      10
ИП3     x#0     86      ИП2     ПП      88      ИП4     С/П     8       +
ИП5     *       ИП4     +       П4      ИП5     1       0       *       П5
В/О

Вводим число, выполняем — на экране результат. При этом -1, 0 и 1 обозначаются соответственно цифрами 7, 8 и 9. Например, введя 123, получим 977778, т. е. «+----0». Особенно забавно, что такой код, показанный нынешним «кодерам-прогерам» с дипломами ЕГЭ-бакалавров, ввергает их в ступор и экзистенциальный ужас (проверено не раз), не говоря уже о предложении написать что-то самим. Но это далеко не самое сложное, что есть в этих калькуляторах. Попробуем же понять их внутреннее устройство, используя для этого JS-код эмулятора.

Внутреннее устройство

В 1990 году Ярослав Карпович Трохименко выпустил книгу «Программируемые микрокалькуляторы: устройство и пользование», в которой досконально описал работу ПМК «расширяющегося ряда» на всех уровнях организации, аппаратных и программных. Хотя там и не был напечатан весь код ПЗУ калькуляторных процессоров, это сократило путь к программному воспроизведению устройств в разы и дало первые объяснения глубинным причинам эффектов «еггогологии».

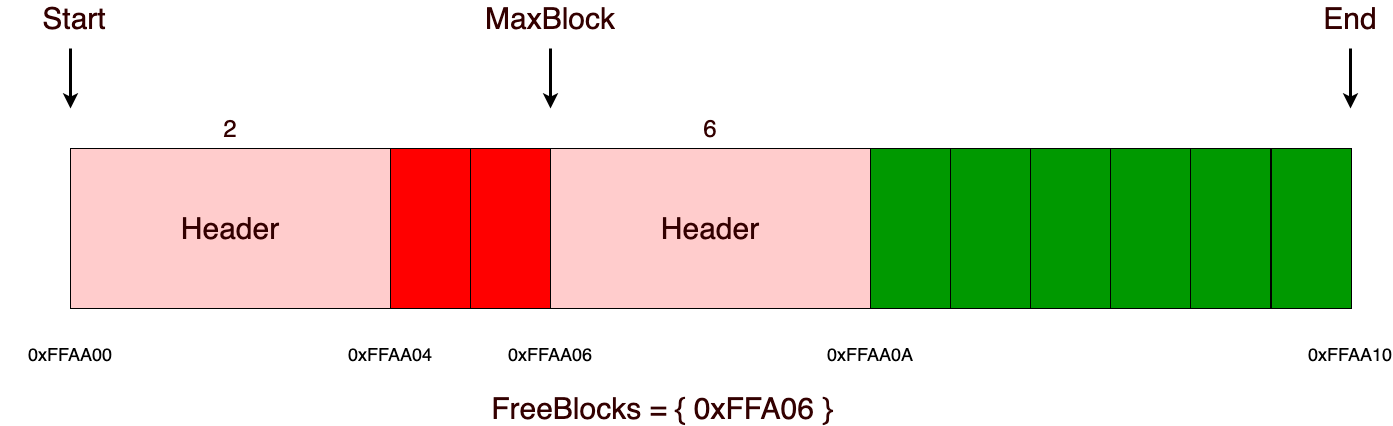
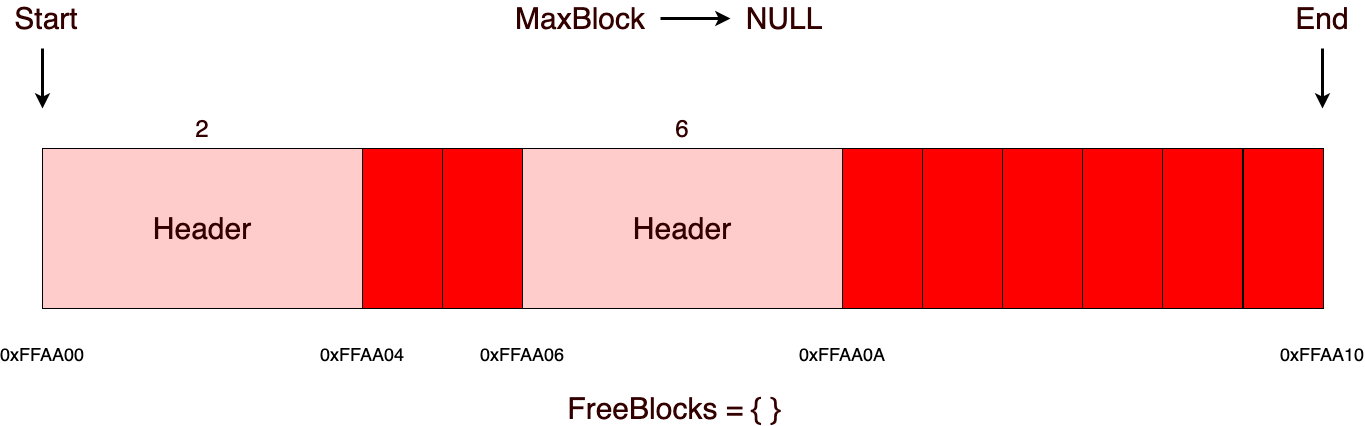
Итак, как уже было сказано выше, МК-61 работает под управлением трёх процессоров К745ИК13, отличающихся только прошивкой (серия К745 — бескорпусные варианты К145). Они соединены однобитной шиной, реализующей последовательное соединение процессоров вместе с микросхемами оперативной памяти К745ИР2 в кольцо. Графически схему калькулятора можно изобразить так:

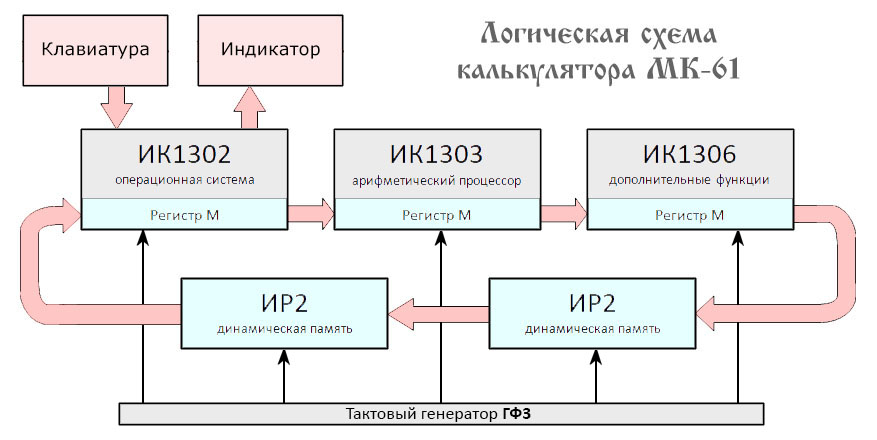
Процессор ИК13 оперирует 4-битными словами. Его динамическая память представлена тремя регистрами M, R и ST объёмом 42 слова каждый, а также регистрами S и S1 размером в одно слово и однобитными ячейками L, T и П. Кроме того, в коде эмулятора имеются переменные для реализации взаимодействия между процессорами, памятью, индикатором, клавиатурой и для сохранения предыдущего состояния.

Память ПЗУ процессора состоит из 256 команд по 23 бита, 128 синхропрограмм, являющихся массивами из девяти шестибитных ячеек, и 68 микрокоманд по 28 битов. Каждая команда содержит три адреса синхропрограмм; ячейки синхропрограммы являются адресами микрокоманд; а биты микрокоманды определяют, какие элементарные операции необходимо выполнить на текущем такте процессора. За один такт выполняется одна микрокоманда и по системной магистрали прогоняется одна тетрада битов, а за 42 такта выполняется одна команда.

constructor(ПЗУ) {
    [this.ПЗУ_микрокоманд, this.ПЗУ_синхропрограмм, this.ПЗУ_команд] =
        [ПЗУ.микрокоманды, ПЗУ.синхропрограммы, ПЗУ.команды];
    this.Сброс();
}

Сброс() {
    [this.M, this.R, this.ST] =
        [new Array(42).fill(0), new Array(42).fill(0), new Array(42).fill(0)];
    [
        this.S, this.S1, this.L, this.T, this.П,
        this.такт, this.команда, this.АСП,
        this.вход, this.выход,
        this.клав_x, this.клав_y
    ] = new Array(12).fill(0);
    this.запятые = new Array(14).fill(false);
    this.обновить_индикатор = false;
}

Выбор микрокоманды для текущего такта

На первом из 42-х такте определяем адрес новой команды, которую мы начинаем исполнять, взяв 4-битное слово из регистра R по адресу 36 в качестве младших разрядов и по адресу 39 в качестве старших, и берём эту команду из кода ПЗУ. Сама команда состоит из трёх адресов синхропрограмм, под которые отведено дважды по 7 битов и третий раз — 8, а также флага, влияющего на выполнение определённой части микрокоманды. Если биты третьего адреса с третьего по последний равны нулю, то обнуляем ячейку T.

if (this.такт == 0) {
    this.команда = this.ПЗУ_команд[this.R[36] + 16 * this.R[39]];
    if ((this.команда >>> 16 & 0b111111) == 0) this.T = 0;
}

Определяем, к какой девятке (по порядку) относится номер такта и какое место в ней занимает. Девятка тактов определяет, какой адрес синхропрограммы, записанный в команде, использовать.

const
    девятка_тактов = this.такт / 9 | 0,
    такт_в_девятке = this.такт - девятка_тактов * 9;

Если это первый такт в девятках с номерами 0, 3 или 4, то следует установить синхропрограмму. Если номер такта относится к первым трём девяткам, то адрес синхропрограммы составляют первые 7 битов команды; если к четвёртой, то вторые 7 битов. А если же к пятой, то берём третьи 8 битов, но в случае, если адрес синхропрограммы больше 31, на первом такте пятой девятки помещаем в регистр R по адресу 37 младшие 4 бита адреса, по адресу 40 — старшие, сам же адрес заменяем на 95 (на любом такте). Таким образом имеется возможность передать два слова в память непосредственно из команды (поэтому поле этого адреса сделано длиннее).

if (такт_в_девятке == 0 && !(девятка_тактов > 0 && девятка_тактов < 3)) {
    if (девятка_тактов < 3)
        this.АСП = this.команда & 0b1111111;
    else if (девятка_тактов == 3)
        this.АСП = this.команда >>> 7 & 0b1111111;
    else if (девятка_тактов == 4) {
        this.АСП = this.команда >>> 14 & 0b11111111;
        if (this.АСП > 31) {
            if (this.такт == 36) {
                this.R[37] = this.АСП & 0b1111;
                this.R[40] = this.АСП >>> 4;
            }
            this.АСП = 95;
        }
    }
}

Определяем адрес микрокоманды, записанный в синхропрограмме. Последняя представляет собой последовательность из 9 адресов микрокоманд, но в массиве они записаны раздельно. Поэтому умножаем вычисленный адрес синхропрограммы на 9, получив индекс её первого элемента, и добавляем к нему значение по следующему правилу: если номер такта — от 0 до 5, то используем его, если от 6 до 20, то берём остаток от деления его на 3, прибавив к нему 3, а если от от 21 до 41, то номер такта в девятке.

let АМК = this.ПЗУ_синхропрограмм[
    this.АСП * 9 +
    (this.такт < 6 ? this.такт : this.такт < 21 ? this.такт % 3 + 3 : такт_в_девятке)
];

На всякий случай отсекаем биты старше 6-го (в коде эмулятора все остальные данные из ПЗУ используются только по частям, что позволяет не беспокоиться о некорректных данных), и если адрес микрокоманды — от 60 до 63, то реализуем условный выбор в зависимости от состояния ячейки L: для значения 0 — чётные номера больше 60, для 1 — нечётные. Таким образом, хоть адрес микрокоманды и 6-битный, но самих микрокоманд 68.

АМК &= 0b111111;
if (АМК > 59) {
    АМК = (АМК - 60) * 2;
    if (this.L == 0) АМК++;
    АМК += 60;
}

Вытаскиваем микрокоманду из кода ПЗУ и разбираем её на массив однобитных микроприказов (флагов), которые далее составляют поля микрокоманды — либо поодиночке, либо в совместно, определяя номер выполняемого действия.

let микрокоманда = this.ПЗУ_микрокоманд[АМК], микроприказы = [];
for (let сч = 0; сч < 28; сч++) {
    микроприказы.push(микрокоманда & 1);
    микрокоманда >>>= 1;
}

Сумматор и клавиатура

На этот раз определяем, к какой уже тройке по порядку относится номер такта и создаём объект сумматора с параметрами α, β, γ и полем суммы Σ. Далее, если микроприказ с номером 25 установлен в 1, используем данные с клавиатуры — параметры x и y, особенные для каждой кнопки (x также используется для передачи меры угла): если следующая за текущей тройка тактов не равна x, то выполняем побитовую дизъюнкцию ячейки S1 с y. После этого проходим по первым 12 микроприказам, выполняя их, если они установлены.

const тройка_тактов = this.такт / 3 | 0;
const сумматор = { альфа: 0, бета: 0, гамма: 0, сигма: 0 };

if (микроприказы[25] == 1 && тройка_тактов != this.клав_x - 1)
    this.S1 |= this.клав_y;

for (let сч = 0; сч < 12; сч++)
    if (микроприказы[сч] == 1)
        this.Выполнить_микроприказ(сч, сумматор);

После этого снова работаем с клавиатурой. Если хотя бы один из битов команды с номерами 18—23 установлен в 1 и y кнопки равен нулю, то обнуляем T. Если же все упомянутые биты нулевые, то устанавливаем значение в массиве запятых на индикаторе равным L, флаг необходимости обновления индикатора, и если при этом следующая тройка тактов равна x, а y больше 0, то записываем y в S1, а в Т — 1. Затем выполняем при необходимости микроприказы с 12, 13 и 14.

if ((this.команда >>> 16 & 0b111111) > 0) {
    if (this.клав_y == 0) this.T = 0;
}
else {
    if (тройка_тактов == this.клав_x - 1 && this.клав_y > 0) {
        this.S1 = this.клав_y;
        this.T = 1;
    }
    this.запятые[тройка_тактов] = this.L > 0;
    this.обновить_индикатор = true;
}

for (let сч = 12; сч < 15; сч++)
    if (микроприказы[сч] == 1)
        this.Выполнить_микроприказ(сч, сумматор);

Теперь складываем входы сумматора, от суммы берём младших 4 бита и кладём в Σ, а 5-й бит (флаг переноса) — в П.

const сумма = сумматор.альфа + сумматор.бета + сумматор.гамма;
сумматор.сигма = сумма & 0b1111;
this.П = сумма >>> 4 & 1;

Поля микрокоманды

Если последний бит команды равен 0 или это последняя девятка тактов (точнее говоря, их в ней всего 6), то определяем значение следующего поля микрокоманды из битов 15, 16 и 17 (в порядке возрастания старшинства). Если полученное значение не равно нулю, то выполняем микроприказ с номером, равным этому полю, увеличенным на 14 (количество уже обработанных микроприказов). Последнее приходится учитывать, поскольку действий предусмотрено 35, а битов в микрокоманде — всего 28, т. е. некоторые биты группируются в поля. При том же условии относительно номера такта или битов 24—31 проходим по микроприказам 18 и 19 (действие определяется номером, увеличенным на четыре — 7 предусмотренных тремя битами действий минус 3 битовых места в микрокоманде).

if ((this.команда >>> 22 & 1) == 0 || девятка_тактов == 4) {
    const поле_микрокоманды =
        микроприказы[17] << 2 |
        микроприказы[16] << 1 |
        микроприказы[15];
    if (поле_микрокоманды > 0)
        this.Выполнить_микроприказ(поле_микрокоманды + 14, сумматор);
    for (let сч = 18; сч < 20; сч++)
        if (микроприказы[сч] == 1)
            this.Выполнить_микроприказ(сч + 4, сумматор);
}

Проходим по микроприказам 20 и 21. Потом следуют три двухбитовых поля, определяющих, соответственно, по три действия (при нулевом значении поля ничего не делается).

for (let сч = 20; сч < 22; сч++)
    if (микроприказы[сч] == 1)
        this.Выполнить_микроприказ(сч + 4, сумматор);

for (let сч = 0; сч < 3; сч++) {
    const поле_микрокоманды =
        микроприказы[23 + сч * 2] << 1 |
        микроприказы[22 + сч * 2];
    if (поле_микрокоманды > 0)
        this.Выполнить_микроприказ(поле_микрокоманды + 25 + сч * 3, сумматор);
}

На выход микросхемы подаётся слово из регистра M, соответствующее номеру такта, после чего вместо него записывается слово, поступившее на вход. Такт увеличивается; если становится равным 42, то обнуляется, — приступаем к обработке следующей команды.

this.выход = this.M[this.такт];
this.M[this.такт] = this.вход;
this.такт++;
if (this.такт == 42) this.такт = 0;

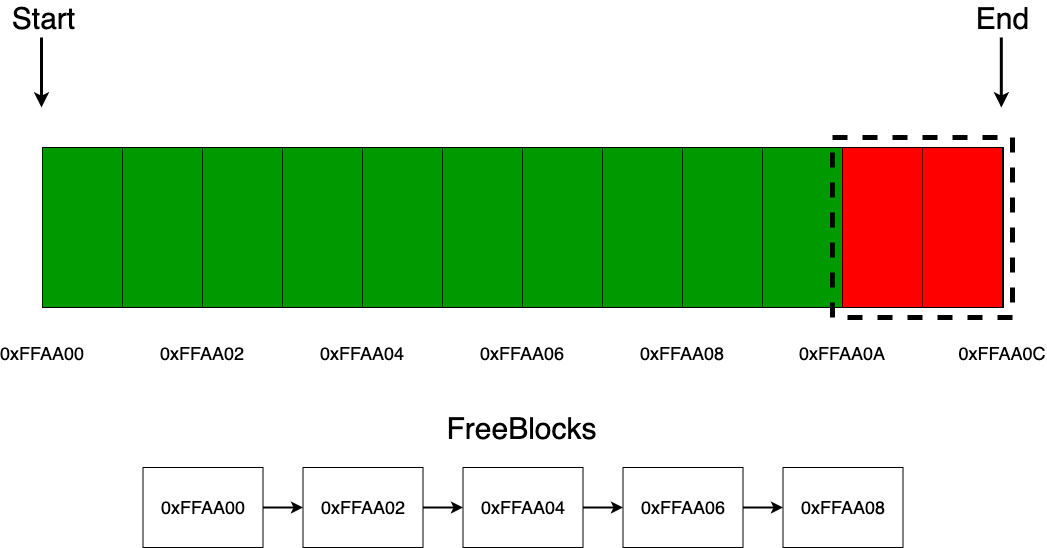
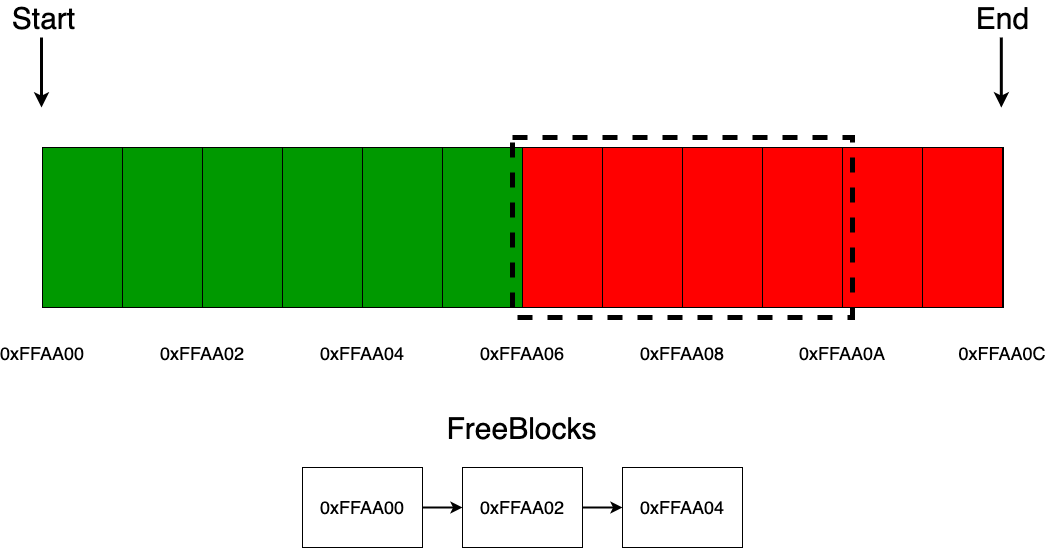
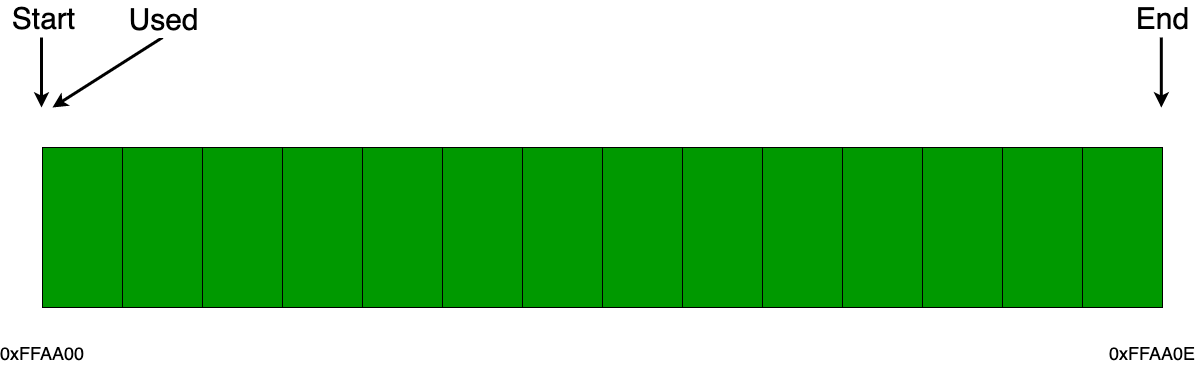
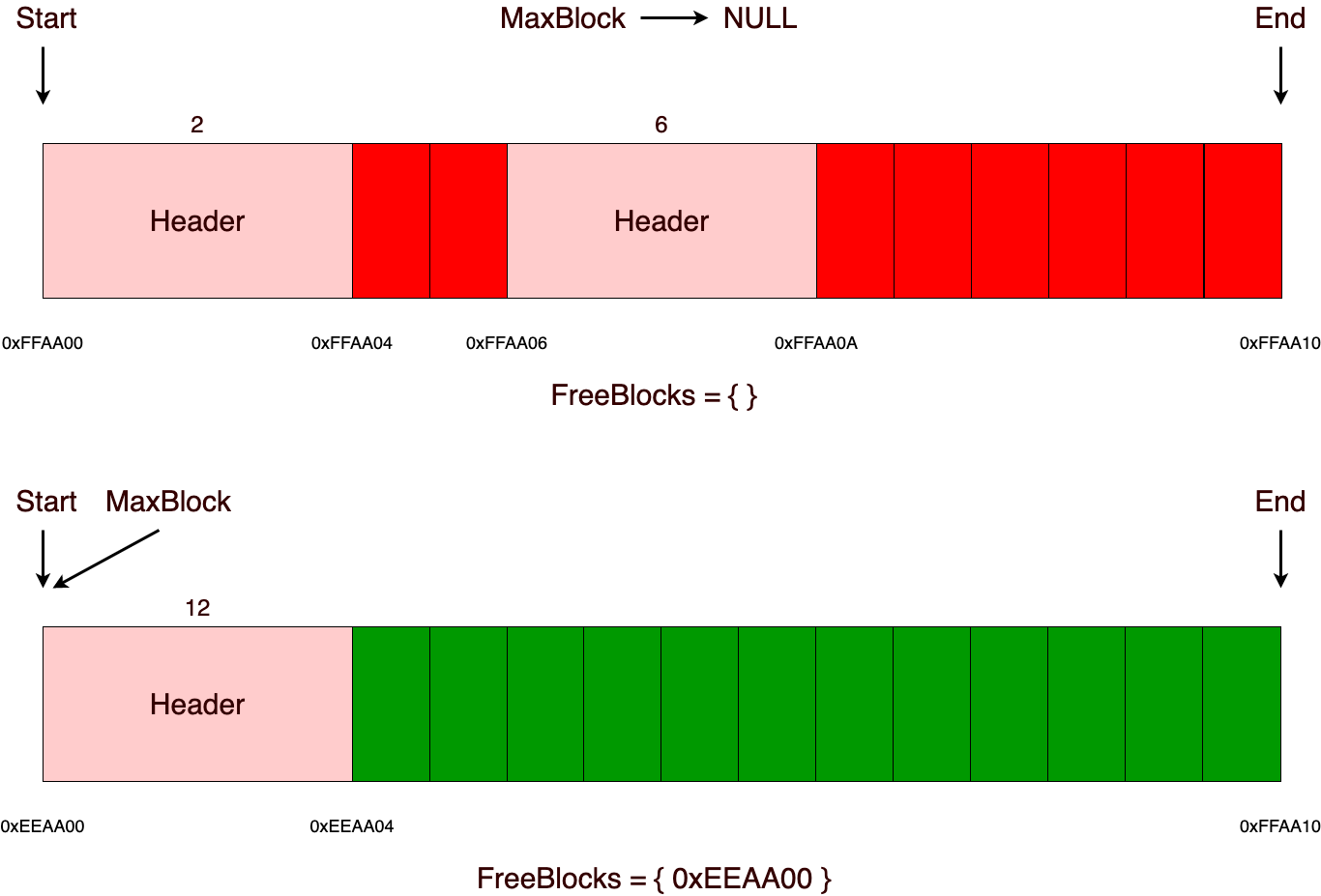
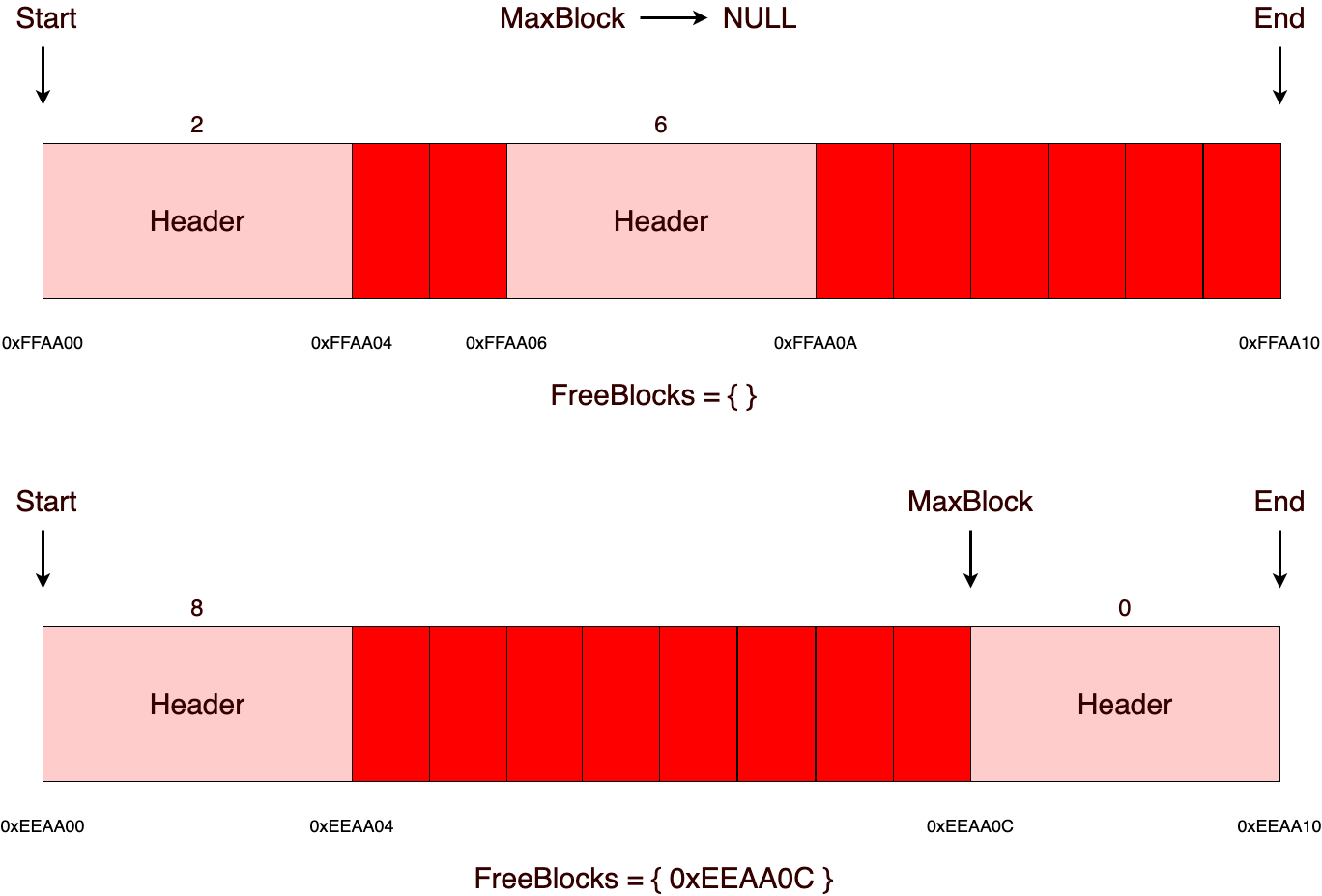
Последний фрагмент собственно составляет также содержание такта памяти ИР2, с той разницей что тактов там 252, как и число слов в единственном регистре M. После выполнения такта одного процессора значение ячейки выхода присваивается ячейке входа следующего процессора или памяти. Чтобы замкнуть кольцо на такте, который был обработан, после прохождения по всем элементам от ИК1302 до второго ИР2 значение выхода последнего передаётся в ячейку первого с номером обработанного только что такта. Память ИР2 вместе с регистрами процессоров ИК13 (не включая сверхоперативные ячейки) можно визуально изобразить так (положение на 84-м такте ИР2):

Микроприказы

А вот и содержание самих микроприказов. Здесь биты микрокоманды с номерами 0—6 влияют на вход сумматора α, 7—11 — на β, 12—14 — на γ. Влияние заключается в побитовой дизъюнкции имеющегося значения входа сумматора с некоторым значением (результат является новым значением входа). Выбор действия с номером от 15 до 21 задаётся трёхбитным полем микрокоманды с битами 15—17, а за действия 22 и 23 отвечают соответственно биты 18 и 19; это всё влияет на регистр R, на слово, задаваемое текущим номером такта, либо на одно из двух предшествующих ему. Предшествующие и следующие адреса берутся по модулю 42, т. е. предыдущим адресом для 0 является 41 (0 — следующим для 41). Биты 20 и 21 задают действия под номерами 24 и 25 соответственно — над регистром M и ячейкой L. Далее идут три двухбитовых поля, отвечающих каждое за три действия — над регистрами S, S1 и ST. В регистре ST операции производятся над тройкой слов, начинающейся с текущего номера такта.

Микроприказы

Выполнить_микроприказ(номер, сумматор) {
    switch (номер) {
        case 0: сумматор.альфа |= this.R[this.такт]; break;
        case 1: сумматор.альфа |= this.M[this.такт]; break;
        case 2: сумматор.альфа |= this.ST[this.такт]; break;
        case 3: сумматор.альфа |= ~this.R[this.такт] & 0b1111; break;
        case 4: if (this.L == 0) сумматор.альфа |= 0xA; break;
        case 5: сумматор.альфа |= this.S; break;
        case 6: сумматор.альфа |= 4; break;
        case 7: сумматор.бета |= this.S; break;
        case 8: сумматор.бета |= ~this.S & 0b1111; break;
        case 9: сумматор.бета |= this.S1; break;
        case 10: сумматор.бета |= 6; break;
        case 11: сумматор.бета |= 1; break;
        case 12: сумматор.гамма |= this.L & 1; break;
        case 13: сумматор.гамма |= ~this.L & 1; break;
        case 14: сумматор.гамма |= ~this.T & 1; break;
        case 15: this.R[this.такт] = this.R[(this.такт + 3) % 42]; break;
        case 16: this.R[this.такт] = сумматор.сигма; break;
        case 17: this.R[this.такт] = this.S; break;
        case 18: this.R[this.такт] = this.R[this.такт] | this.S | сумматор.сигма; break;
        case 19: this.R[this.такт] = this.S | сумматор.сигма; break;
        case 20: this.R[this.такт] = this.R[this.такт] | this.S; break;
        case 21: this.R[this.такт] = this.R[this.такт] | сумматор.сигма; break;
        case 22: this.R[(this.такт + 41) % 42] = сумматор.сигма; break;
        case 23: this.R[(this.такт + 40) % 42] = сумматор.сигма; break;
        case 24: this.M[this.такт] = this.S; break;
        case 25: this.L = this.П; break;
        case 26: this.S = this.S1; break;
        case 27: this.S = сумматор.сигма; break;
        case 28: this.S = this.S1 | сумматор.сигма; break;
        case 29: this.S1 = сумматор.сигма; break;
        case 30: this.S1 = this.S1; break;
        case 31: this.S1 = this.S1 | сумматор.сигма; break;
        case 32:
            this.ST[(this.такт + 2) % 42] = this.ST[(this.такт + 1) % 42];
            this.ST[(this.такт + 1) % 42] = this.ST[this.такт];
            this.ST[this.такт] = сумматор.сигма;
        break;
        case 33: {
            const x = this.ST[this.такт];
            this.ST[this.такт] = this.ST[(this.такт + 1) % 42];
            this.ST[(this.такт + 1) % 42] = this.ST[(this.такт + 2) % 42];
            this.ST[(this.такт + 2) % 42] = x;
        } break;
        case 34: {
            const
                x = this.ST[this.такт],
                y = this.ST[(this.такт + 1) % 42],
                z = this.ST[(this.такт + 2) % 42];
            this.ST[this.такт] = сумматор.сигма | y;
            this.ST[(this.такт + 1) % 42] = x | z;
            this.ST[(this.такт + 2) % 42] = y | x;
        } break;
    }
}

Так работает один процессор, выполняя одну микрокоманду. В режиме исполнения программы реальный калькулятор выполняет около 3–4 шагов пользовательской программы в секунду, примерно на такую же скорость работы настроен и эмулятор. Для прохождения одного шага такт повторяется 23520 раз, выполняя 560 команд, прописанных в коде ПЗУ.

Это обстоятельство и сам довольно нетривиальный алгоритм исполнения кода делают реконструкцию механизмов и алгоритмов работы, запрограммированных в коде микросхем этих калькуляторов, очень и очень затруднительной. Достоверно и детально описать, как это работает, могли лишь причастные к разработке этих устройств; сегодня же любителям советских программируемых калькуляторов, интересующимся этой темой, остаётся лишь тоскливо рассматривать под лупой каждый бит восстановленного кода и пытаться понять, зачем он нужен.

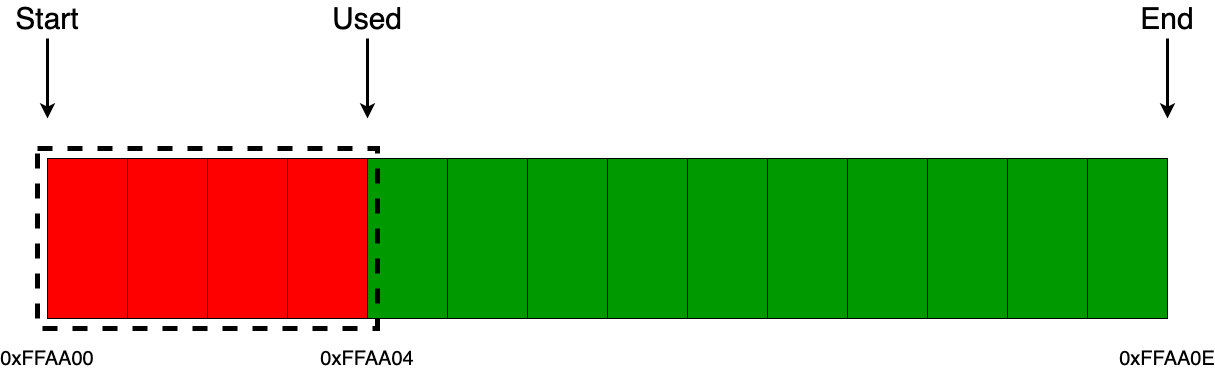
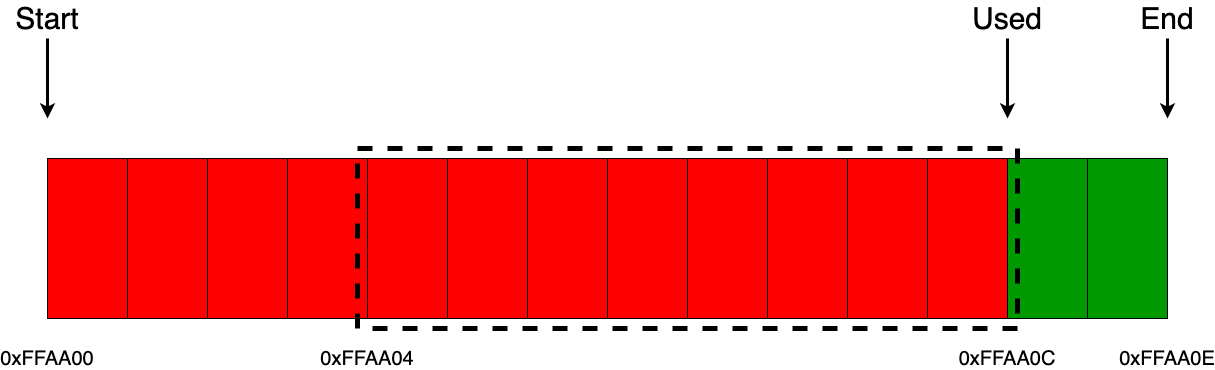
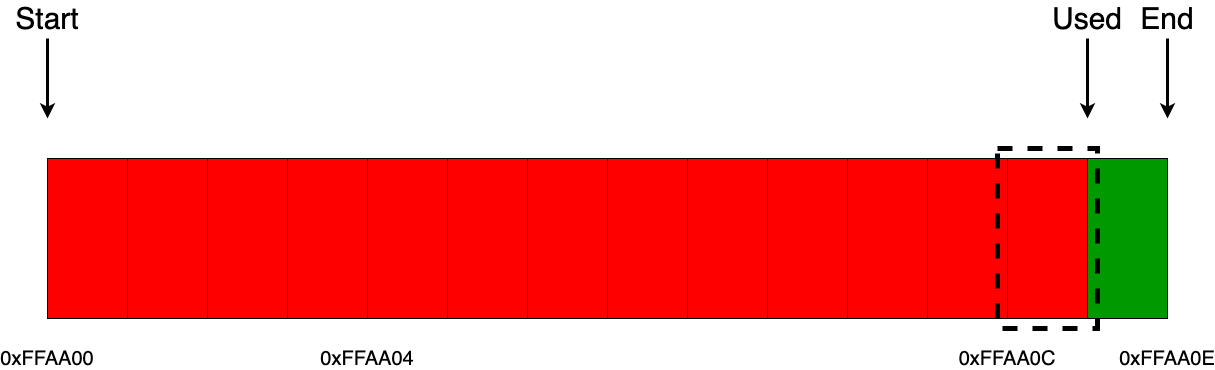
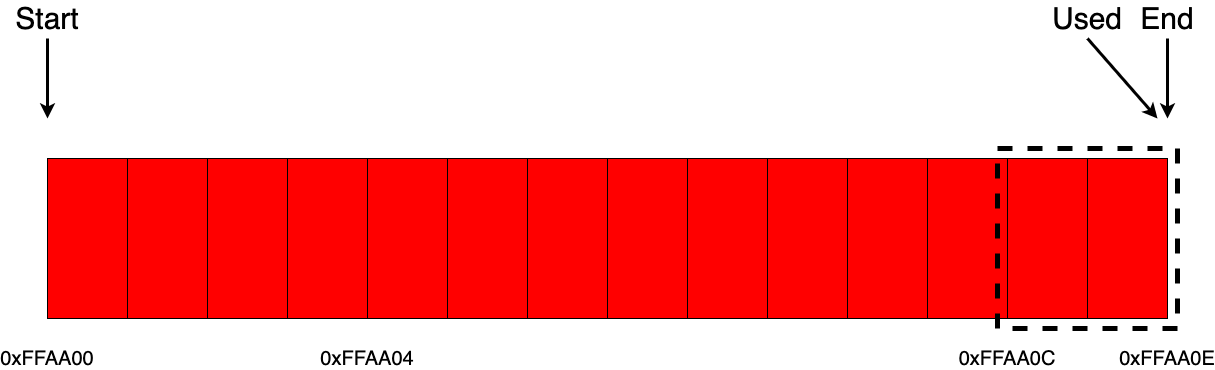
Впрочем, некоторые моменты благодаря эмулятору и книге «Устройство и пользование» всё же удалось прояснить. Например, стало понятно, как возникают числа с порядком больше 99, работа с которыми была одним из основных направлений «еггогологии» – т. н. «электронный океан чисел». Разряды числа в памяти хранятся в двоично-десятичной форме, т. е. одна тетрада битов кодирует одну десятичную цифру (хотя может кодировать и шестнадцатеричную). Сами числа представлены в экспоненциальной форме и занимают 12 ячеек (вообще 14 – треть от длины регистра, но два разряда – служебные), при этом первая ячейка обозначает знак порядка, следующие две – сам порядок, потом ещё одна ячейка – знак мантиссы и восемь – собственно мантисса. Хотя на знак отведено аж четыре бита, используются только два значения – 0 для положительных чисел и нуля и 9 для отрицательных. Так вот, при переполнении следующий разряд порядка записывается в ячейку его знака, т. е. $\$inline\$10\; ^\; \{50\}\; \backslash times\; 10\; ^\; \{50\}\$inline\$$ даёт «$\$inline\$ЕГГОГ\$inline\$$», но в памяти записан порядок $\$inline\$[1]\; [0]\; [0]\$inline\$$, где единица стоит в ячейке знака. Над этим значением можно производить некоторые операции, как над обычным числом, правда, до тех пор, пока порядок находится в пределах второй сотни – дальше начинаются сложности (причём над «ЕГГОГом», полученным именно таким способом; полученный при делении на 0, например, ничего не даст). Однако глубинные механизмы «числового океана» всё же так и остались невыясненными.

Используя эмулятор, можно, например, изучить содержание памяти калькулятора во время каких-либо манипуляций или же прогонять код по одному такту или команде, можно посмотреть на порядок выполнения команд каждого процессора или попробовать добавлять или убирать устройства с системной магистрали. Но насколько это позволит продвинуться в изучении работы МК-61?..

---

Завершить эту заметку хочу цитатой, которая, на мой взгляд, хорошо резюмирует написанное выше.

Программирование МК-61 имеет глубокий философский подтекст.

Ограниченность ресурсов и доступного инструментария, добровольно принимаемая программистом, отражает собой многовековой опыт аскетических духовных практик. Сложнейшая многоуровневая иерархия программ управления калькулятором – от кода, вводимого человеком, до микрокоманд и микроприказов — есть отражение необычайной сложности божественного мироздания, всех глубин и уровней материи – от крупномасштабных структур вселенной до элементарных частиц, от сознания до неживой материи, от социума до первозданного хаоса и небытия.

Сам микрокод, прошитый в ПЗУ калькулятора, предстаёт объектом благоговейного созерцания, ибо никто не может в полной мере постичь принципы его работы, структуру или как-либо повлиять на его работу, склоняя нас к агностицизму и мыслям об иллюзорности свободы воли. Тройственность структуры микрокода – команды, синхропрограммы и микрокоманды – и три процессора калькулятора отсылают нас к вытекающей из христианского представления о Боге как о Троице троичности бытия, к естественной (троичной) аристотелевой логике и к концепции триединой русской нации.

Программа, подаваемая человеком калькулятору, представляя собой с одной стороны низкоуровневый автокод, составленный из элементарных команд, с другой же – высокоуровневые инструкции, исполняемые прошивкой ПЗУ, демонстрирует нам диалектический закон единства и борьбы противоположностей. Исполнение же программы, когда, пройдя 105 шагов программной памяти, калькулятор возвращается в начало и продолжает исполнение кода, есть образ колеса сансары, а получение решения задачи становится подобием нирваны, достигнутой в результате правильно написанной и выполненной программы.

Let's block ads! (Why?)