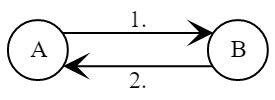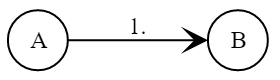...

суббота, 16 ноября 2019 г.

Бессмысленные совещания на работе на самом деле «являются формой терапии»

Исследователи из университета Мальмё в Швеции пришли к выводу, что собрания на работе следует рассматривать скорее как форму «терапии», а не способ принятия решений. Там люди получают возможность продемонстрировать свой статус, а также снять стресс.

Профессор политологии Патрик Холл (Patrik Hall) из университета Мальмё говорит, что в современных компаниях наблюдается некое противоречие: собирается больше совещаний, но на них принимается мало решений. И хотя многие рядовые сотрудники выражают низкую оценку этим собраниям, но число таких мероприятий продолжает расти.

Политолог говорит, что увеличение числа встреч отражает изменения в численности и качестве персонала: в фирмах становится меньше людей, непосредственно выполняющих работу, а больше тех, кто занимает «коммуникативные» и «совещательно-интенсивные» должности: это стратеги, советники, консультанты и менеджеры.
По мнению профессора, в компаниях выросла численность сотрудников на управленческих должностях, которые часто не очень хорошо определены, и где «иерархия не так ясна». Эти люди не заняты конкретной разработкой продукта.

«Многие менеджеры не знают, что делать», — объясняет Патрик Холл, а когда они «не уверены в своей роли», то реагируют на это генерацией ещё большего количества совещаний: «Люди любят поговорить, и это помогает им найти свою роль». Многие из этих людей могут проводить половину своего рабочего времени на собраниях.

Встречи могут «вызвать чувство бессмысленности», говорит Холл. Но он утверждает, что многие не понимают истинный смысл этих мероприятий. В какой-то момент такие совещания — особенно длительные — начинают выполнять «почти терапевтическую» функцию.

Независимо от заявленной задачи совещания, оно представляет «возможность пожаловаться и получить признание коллег». В то же время исследования показывают, что ощущение бессмысленности приводит к тому, что некоторые участники совещаний могут потерять терпение — и проводить большую часть времени, играя со своими мобильными телефонами.

Некоторые находят совещания неприятной тратой времени и задаются вопросом, почему должны их терпеть. Но учёный утверждает, что негативное отношение к встречам может быть вызвано тем, что их реальные цели неправильно поняты. Истинной целью таких встреч может быть утверждение авторитета организации — напоминание сотрудникам, что они являются её частью. Такие встречи на самом деле не ставят задачу принять какое-то решение, говорит Холл.

Профессор Холл даёт некоторые рекомендации, чтобы повысить эффективность совещаний. Он предлагает бронировать комнаты на более короткие промежутки времени, поскольку опыт показывает, что обычно совещания затягиваются на весь отведённый период, сколько бы на него не выделялось. Очень редко они заканчиваются раньше срока.

Кроме того, важно «равенство» участников: «Когда вы встречаетесь с коллегами на одном уровне, как профессионал, вы можете обсудить различные вопросы, которые вас интересуют», — говорит он. Когда же на совещаниях доминируют разные уровни статуса, они становятся «борьбой за власть» и оставляют разочарование.

«Люди часто чувствуют себя маргинализированными. Они чувствуют, что них никакого влияния или положения в компании. В этих случаях складывается впечатление, что встречи ничего не улучшают, а на самом деле вызывают ещё большее разочарование», — так профессор объясняет распространённое мнение, что многие совещания представляют собой пустую трату времени.

Let's block ads! (Why?)

на Комментариев нет:
Ярлыки: ,

«Услышать» космос: от темной материи до кометы Чурюмова — Герасименко

Известно, что звук в безвоздушном пространстве не распространяется. Но назвать космос немым нельзя. Рассказываем, как «звучат» планеты и другие космические объекты, и где их послушать.


Фото NASA / Unsplash

Радио для темной материи


Темная материя — составляет большую часть Вселенной. Ученым известно (благодаря гравитационным аномалиям), что темная материя существует, но зарегистрировать её пока не удалось. Она не излучает свет, а также любое другое электромагнитное излучение, видимое современным телескопам. Группа физиков предложила способ детекции темной материи — «послушать» её. Они разрабатывают своеобразное «радио», на основе детекторов гравитационных волн. Они будут улавливать аксионы — гипотетические нейтральные частицы, удерживающие протоны и нейтроны вместе — составляющие существенную часть холодной тёмной материи.
В этом году физики из Стокгольмского университета предложили подход, который усилит эффект «радио». Они предположили, что электрическое поле аксионов можно использовать для создания колебаний в плазме, что сделает сигнал более явным.

Отметим, что в 2017 году аналогичный проект начали развивать в Стэндфордском университете. В основу их «радио» для темной материи легла концепция корпускулярно-волнового дуализма. Она предполагает, что материальные микроскопические объекты при одних условиях проявляют свойства волн, а при других — свойства частиц. И эти волны можно зарегистрировать с помощью антенн и резонаторов. Нужно лишь настроиться на частоту темной материи. Вероятно, сигнал будет очень слабым, поэтому инженеры дополнительно разрабатывают высокочувствительные магнитометры. Они могут чувствовать поля с индукцией менее одного фемтогаусса. Пока ученые пытаются «расслышать» темную материю, некоторые звуки космоса можно послушать уже сейчас.

Черная дыра и «голос» Юпитера


Чтобы мы могли услышать, как «звучат» планеты и другие небесные тела, физики преобразуют электромагнитные волны в звуковые. Это творческий процесс, который похож на создание музыки. Впервые космическое излучение преобразовали в звук в 1996 году. Тогда зонд «Галилео» сделал запись электромагнитных волн Юпитера. Правда, позже оказалось, что это были заряженные частицы от спутника планеты — Ганимеда.


Сделать нужную аудиозапись удалось в 2016 году. Тогда НАСА опубликовало запись с космического аппарата «Юнона» в момент его вхождения в магнитосферу Юпитера. Зонд передал на Землю звуки, которые возникли при взаимодействии магнитного поля планеты и солнечного ветра.
Существует аналогичная запись с Сатурна. Её сделал зонд «Кассини», который вылетел с Земли в 1997 году. Источник радиоволн, которые издает Сатурн, — полярное сияние на полюсах планеты длительностью от нескольких минут до часа. Акустический фон газового гиганта характеризуется большим количеством высоких и низких тонов и постоянным изменением частоты звучания.

В 2014 году аппарат «Филы» с зонда «Розетта» высадился на поверхность кометы Чурюмова — Герасименко. Там он зафиксировал издаваемый ей звук с помощью инструмента для изучения плазменной среды. Комета «поет» на частоте 40–50 мГц — вибрации вызывают частицы плазмы, проходящие сквозь магнитное поле.
Если говорить о других небесных телах, то еще в 2003 году физики из Кембриджа под руководством Эндрю Фабиана (Andrew Fabian) обнаружили «поющую» черную дыру в кластере Персея — в центре скопления галактик. Астрономы использовали телескоп «Чандра». Он улавливал рентгеновское излучение, которое исходило из самого центра кластера. Так ученые выявили звуковые волны от сверхмассивной черной дыры.

Скопление галактик способствует тому, что космический газ «пульсирует» из-за множества гравитационных воздействий — он и издает низкий «звук», указывающий на изменение давления в черной дыре. Ученые считают, что она поет уже многие миллиарды лет, а издаваемый ей шумовой фон на 57 октав ниже ноты «до». Это — за пределами слышимости человеческого уха.

Музыка с «Хаббла»


Сотрудники НАСА превратили в «музыку» ультразвуковые данные, которые получил телескоп «Хаббл». Каждому элементу на сделанных снимках специальный компьютерный алгоритм назначил свой звук. Звездам и небольшим галактикам присвоил короткие звуки, а спиральным галактикам — длинные.

Многие западные издания назвали эту «музыку» жуткой и пугающей. Кстати, у NASA есть собственный аккаунт в SoundCloud — там агентство выкладывает не только тематические подкасты, но и другие звуки из космоса.



О чем еще мы пишем в нашем «Мире Hi-Fi»:

Российские ученые записали музыку космических пульсаров
Новый ультразвуковой сенсор позволит «послушать» бактерии — как он устроен
«Послушай, чтобы найти поломку»: аудиозаписи неисправных индустриальных машин
«Стервозная Бетти» и современные аудиоинтерфейсы: почему они говорят женским голосом?
Аудиоинтерфейсы: звук как источник информации на дороге, в офисе и в небе
«Гул Земли»: теории заговора и возможные объяснения

Let's block ads! (Why?)

на Комментариев нет:
Ярлыки: ,

[Из песочницы] Дизайн интерфейса для игры, рисуем кольцо Хавеля из Dark Souls 3

Здравствуйте, дорогие друзья!

Я Михаил Кравченко, дизайнер игровых интерфейсов.

Это статья о том как нарисовать кольцо Хавеля из игры Dark Souls 3. Перед вами результат, которого я добился примерно за полтора часа работы в фотошопе.

Дизайнера интерфейсов периодически просят нарисовать несколько иконок для игры, например, когда художник в отпуске и что-то срочно понадобилось. Так что иметь такой навык в своем арсенале довольно полезно. Ниже я опишу процесс рисования иконки.
Иконки удобно рисовать в большом размере, а потом уменьшать до нужного. Это позволяет рисовать довольно небрежно, а при уменьшении картинки небрежно нарисованные места перестают быть заметными. Я обычно выбираю размер в 4 раза больше чем тот, что понадобится в итоге. На картинке ниже показана иконка в увеличенном размере, как видите, она нарисована довольно небрежно.

Референсы


Референсы — это изображения, которые помогают изучить предмет. Глядя на них мы понимаем как он освещен, какая у него фактура и цвет. И все это помогает улучшить наш результат.

Например, если мы собираемся нарисовать камень, нужно найти несколько фоток камней, изучить их и только потом рисовать. А в процессе рисования обязательно держать фотки на видном месте и периодически на них поглядывать. В нашем случае в качестве референса выступает кольцо из игры.

Набросок


Набросок нужен чтобы обозначить основные формы, из которых состоит предмет. При создании наброска нужно идти от общего к частному — сперва наметить габаритные размеры предмета, а потом уточнить его детали. Если мы сразу перейдем к мелким деталям, то скорее всего напортачим с габаритными размерами и в результате получим кривой предмет.

У меня есть круглая жесткая кисть для набросков, параметры alpha и flow выставляю в районе 30%. Они также меняются от силы нажатия на перо. Такая кисть позволяет постепенно уточнять детали наброска и находить нужную форму. Ниже вы видите настройки кисти.

Ставим слева референс, а справа рисуем набросок. В итоге получаем примерно такой результат.

Силуэт


Далее идет работа с силуэтом предмета. Нужно создать новый слой и выбрать обычное лассо.
Хоткей на создание нового слоя — Ctrl+Shift+N, а лассо можно найти на панели инструментов, или вызвать клавишей L.

Обведем предмет с помощью лассо. Можно делать это по частям, удерживая клавишу Shift. После чего зальем выделенную область цветом, нажав Alt + Backspace. Получим залитый силуэт, выделенный по периметру.

Завернем слой с заливкой в группу — кликнем на него и нажмем Ctrl+G. На панели слоев появится папка, а в ней будет слой с заливкой.

Кликнем по папке и нажмем на иконку маски в нижней части панели слоев.

На группе появляется значок маски.

Теперь можно рисовать на слоях внутри группы и не бояться вылезти за границы силуэта предмета. Маска спрячет всё что находится за ними.

Объем


Дальше покажем объем предмета. Сперва десатурируем наш референс. На этом этапе цвета будут нам только мешать, поэтому нужно их отключить. Кликаем на слой с референсом и создаем поверх него корректирующий слой для параметров hue saturation.

Зажимаем Alt и кликаем между слоями. Теперь корректирующий слой приклеился к слою с референсом и влияет только на него. Кликаем на корректирующий слой и передвигаем ползунок saturation до упора влево.

Картинка стала черно-белой.

Создадим новую группу в нашей группе с маской, в ней будут слои, в которых мы покажем объем. Вот как это работает. Берем лассо и выделяем светлые области предмета, потом заливаем их белым цветом и регулируем прозрачность слоя, чтобы результат стал ближе к референсу.

Прозрачность слоя регулируется вот здесь.

Ее также можно изменять, нажимая цифры на клавиатуре. Цифра 1 — 10%, 2 — 20%, 3 — 30% и так далее. Дальше создаем новый слой и повторяем процедуру для более светлых участков предмета, а потом делаем то же самое для темных участков. Ниже вы видите несколько таких шагов.

В итоге получилась болванка с объемом.

Текстуры


Следующим шагом набросим на предмет текстуры. Как и на прошлом этапе, нужно сделать новую папку и создать в ней несколько слоев с режимом наложения Soft light.

Режим выставляется здесь:

Потом берём текстурную кисть и проходимся по всей поверхности предмета. Текстурные кисти бывают большими и порой за ними не видно предмета, который мы рисуем. Чтобы скрыть очертания кисти, жмем на CapsLock.

Как и на прошлом этапе, можно использовать несколько слоев. В итоге болванка станет шероховатой и можно будет двигаться дальше.

Детали


Снова создаем отдельную группу и слои в ней.

Берём жесткую кисточку и прорабатываем детали. Если выбрать кисточку и нажать Alt, она превратится в пипетку и позволит брать цвета прямо с рисунка. Сперва работаем большой кистью, а потом постепенно уменьшаем ее. Горячие клавиши на изменение размера кисточки — это квадратные скобки. Левая уменьшает кисть, а правая — увеличивает.

Если нужно показать четкие формы, можно использовать лассо. Выделить нужную область и провести по ней кистью. Когда мы выделяем какую-то область с помощью лассо, по ее периметру образуются бегущие контуры. Чтобы они не мешали, их можно отключить, нажав Ctrl + H.

Еще в какой-то момент вы можете заметить, что картинке не хватает объёма. Это можно исправить, создав слой с режимом наложения Softlight и дорисовав недостающий объем мягкой кистью. Добавлять его лучше постепенно, используя кисть с прозрачностью. В итоге у нас получается чёрно-белое изображение предмета близкое к оригиналу.

Цвета


Мы закончили с формой и можем добавить цвета. Прячем или удаляем корректирующий слой референса, опять берем новый слой и новую группу. Для слоя выбираем режим наложения color. Берем мягкую полупрозрачную кисть и понемногу добавляем цвет на предмет. Напомню — если выбрать кисть и зажать Alt, она превратится в пипетку и мы можем брать цвета прямо с референса.

Кстати, прозрачность кисти можно менять, нажимая клавиши с цифрами на клавиатуре. 1 — 10%, 2 — 20% и так далее. Как и на прошлых этапах, мы можем использовать несколько слоев и регулировать их прозрачность, чтобы менять интенсивность цвета и добиваться результата близкого к референсу.

Оставшиеся детали


Последним этапом уточняем оставшиеся детали. Нам снова понадобится новая группа и новые слои в ней. На этом этапе добиваемся максимального сходства с референсом.

Готово.

Надеюсь что эта статья была для вас полезной, исходник и кисти можно скачать по ссылкам ниже.

Кисти
Исходник

Всем удачи, и творческих успехов.

Let's block ads! (Why?)

на Комментариев нет:
Ярлыки: ,

Государственные органы штата Калифорния не будут покупать автомобили на ДВС

Начиная от 15.11.2019 правительственные учреждения штата Калифорния не будут покупать седаны, которые работают на ДВС. А начиная с января — перестанут покупать любые автомобили на ДВС у компаний, которые не соглашаются с Калифорнийскими правилами по выбросам и расходам топлива.
Да, очень жестко и очень быстро калифорнийцы отреагировали на давление со стороны автопроизводителей, а также федеральных властей на счет того, что они не вправе регулировать и устанавливать правила на счет уровня выбросов парниковых газов, а также среднего расхода топлива для каждого производителя.
В 2018-м году штат потратил 74 миллионов долларов США на приобретение транспортных средств, что было эквивалентом 2672 единиц техники.

Самая цифра — не очень большая. Но это определенный звоночек. Если мы не можем повлиять на правила, значит будет голосовать кошельком.
Предположу, что если эти решения останутся в силе, то после этого могут быть введены и более жесткие меры, например, въезд в город на ДВС — под запретом или же могут обложить дополнительными налогами владельцев автомобилей или же продавцов ископаемого топлива. В любом случае, это определенные шаги, которые могут подхватить и другие штаты, как это было с «зелеными» кредитами.
Также стоит напомнить, что в Калифорнии продается почти половина автомобилей Тесла, которые реализовываются в США.
Источник новости

Let's block ads! (Why?)

на Комментариев нет:
Ярлыки: ,

«Криптосистемы-протоколы»: Диффи—Хеллмана, Эль-Гамаля, MTI/A(0), STS

Предисловие
Данный текст будет являться одной из переписанных глав для учебного пособия по защите информации кафедры радиотехники и систем управления, а также, с этого учебного кода, кафедры защиты информации МФТИ (ГУ). Полностью учебник доступен на github (см. также draft releases). На Хабре планирую выкладывать новые «большие» куски, во-первых, чтобы собрать полезные комментарии и замечания, во-вторых, дать сообществу больше обзорного материала по полезным и интересным темам. Предыдущие разделы главы «Криптографически протоколы»: 1, 2, 3

Как и создатели трёхпроходных протоколов из предыдущего раздела, авторы следующих алгоритмов считали их не просто математическими конструкциями, обеспечивающие некоторую элементарную операцию (например, шифрование с открытым ключом), но пытались вокруг одной-двух формул построить законченную систему распространения ключей. Некоторые из этих конструкций, преобразовавшись, используются до настоящего времени (например, протокол Диффи-Хеллмана), некоторые — остались только в истории криптографии и защиты информации.

Позже в 1990-х годах будут разделены математические асимметричные примитивы (шифрование и электронная подпись) и протоколы, эти примитивы использующие, что будет продемонстрировано в разделе про асимметричные протоколы.

Протокол Диффи—Хеллмана


Первый алгоритм с открытым ключом был предложен Диффи и Хеллманом в работе 1976 года «Новые направления в криптографии» (Bailey Whitfield Diffie, Martin Edward Hellman, «New directions in cryptography», [Diffie, Hellman 1976]). Данный протокол, который также можно назвать схемой Диффи—Хеллмана, стал первым, позволивший уменьшить требования к каналу связи для установления защищённого соединения без предварительного обмена ключами.

Протокол позволяет двум сторонам создать общий сеансовый ключ используя такой канал связи, который может прослушивать злоумышленник, но в предположении, что последний не может менять содержимое сообщений.

Пусть $p$ — большое простое число, $g$ — примитивный элемент группы $\mathbb{Z}_p^*$, $y = g^x \bmod p$, причём $p$, $y$ и $g$ известны заранее. Функцию $y=g^{x} \bmod p$ считаем однонаправленной, то есть вычисление функции при известном значении аргумента является лёгкой задачей, а её обращение (нахождение аргумента) при известном значении функции — трудной. (Обратную функцию $x = \log_g y \bmod p$ называют функцией дискретного логарифма. В настоящий момент не существует быстрых способов вычисления такой функции для больших простых $p$.)

Протокол обмена состоит из следующих действий.

Взаимодействие участников в протоколе Диффи—Хеллмана
  1. Алиса выбирает случайное $2 \leq a \leq p - 1$
    $Alice \to \left\{ A = g ^ a \bmod p \right\} \to Bob$
  2. Боб выбирает случайное $2 \leq b \leq p-1$
    Боб вычисляет сессионный ключ $K = A ^ b \bmod p$
    $Bob \to \left\{ B = g ^ b \bmod p \right\} \to Alice$
  3. Алиса вычисляет $K = B ^ a \bmod p$

Таким способом создан общий секретный сессионный ключ $K$. За счёт случайного выбора значений $a$ и $b$ в новом сеансе будет получен новый сессионный ключ.

Протокол обеспечивает только генерацию новых сессионных ключей (цель G10). В отсутствие третей доверенной стороны он не обеспечивает ни аутентификацию сторон (цель G1), из-за отсутствия проходов с подтверждением владения ключом отсутствует аутентификация ключа (цель G8). Зато, так как протокол не использует длительные «мастер»-ключи, можно говорить о том, что он обладает свойством совершенной прямой секретности (цель G9).

Протокол можно использовать только с такими каналами связи, в которые не может вмешаться активный криптоаналитик. В противном случае протокол становится уязвим к простой «атаке посередине».

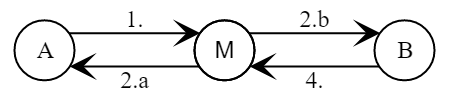
Взаимодействие участников в протоколе Диффи—Хеллмана в модели с активным криптоаналитиком
  1. Алиса выбирает случайное $2 \leq a \leq p - 1$
    $Alice \to \left\{ A = g ^ a \bmod p \right\} \to Mellory~(Bob)$
  2. Меллори выбирает случайное $2 \leq m \leq p-1$
    Меллори вычисляет сессионный ключ для канала с Алисой

    $K_{AM} = A ^ m \bmod p = g ^ {am} \bmod p$


    $Mellory~(Alice) \to \left\{ M = g ^ m \bmod p \right\} \to Bob$
    $Mellory~(Bob) \to \left\{ M = g ^ m \bmod p \right\} \to Alice$
  3. Алиса вычисляет сессионный ключ для канала с Меллори (думая, что Меллори это Боб)

    $K_{AM} = M ^ a \bmod p = g ^ { am } \bmod p$

  4. Боб выбирает случайное $2 \leq b \leq p-1$
    Боб вычисляет сессионный ключ для канала с Меллори (думая, что Меллори это Алиса)

    $K_{BM} = M ^ b \bmod p = g ^ { bm } \bmod p$


    $Bob \to \left\{ B = g ^ b \bmod p \right\} \to Mellory~(Alice)$
  5. Меллори вычисляет сессионный ключ для канала с Бобом

    $K_{BM} = B ^ m \bmod p = g ^ { bm } \bmod p$



В результате Алиса и Боб получили новые сессионные ключи, но «защищённый» канал связи установили не с друг с другом, а со злоумышленником, который теперь имеет возможность ретранслировать или изменять все передаваемые сообщения между Алисой и Бобом.

Протокол Диффи—Хеллмана отличается от большей части протоколов распространения ключей из-за того, что не использует другие криптографические примитивы (функции шифрования, электронно-цифровой подписи или хеширования), но сам по себе является в некотором смысле криптографическим примитивом для построения более сложных протоколов. Он обеспечивает генерацию случайного числа в распределённой системе без доверенного центра. Причём ни одна из сторон не может заставить другую сторону использовать старый сессионный ключ, в отличие от, например, протокола Yahalom.

Протокол можно изменить таким образом, чтобы вместо мультипликативной группы простого умножения использовать аддитивную группу сложения точек эллиптической кривой. В этом случае стороны по прежнему будут выбирать некоторые случайные целые числа, но не возводить генератор-число в степень, а умножать генератор-точку на загаданное число.

  1. Стороны договорились о группе точек эллиптической кривой $\mathbb{E}$, её циклической подгруппе $\mathbb{G}$ мощности $n = \| \mathbb{G} \|$ и генераторе $G$ группы $\mathbb{G}$ (или хотя бы достаточно большой подгруппы группы $\mathbb{G}$).
  2. Алиса выбирает случайное $2 \leq a \leq n - 1$
    $Alice \to \left\{ A = a \times G \right\} \to Bob$
  3. Боб выбирает случайное $2 \leq b \leq n - 1$
    Боб вычисляет точку $K = b \times A$
    $Bob \to \left\{ B = g \times G \right\} \to Alice$
  4. Алиса вычисляет точку $K = a \times B$

В качестве нового сессионного ключа стороны могут выбрать, например, первую координату найденной точки $K$.

Протокол Эль-Гамаля


Протокол Эль-Гамаля ([ElGamal, 1984], [ElGamal, 1985]) за счёт предварительного распространения открытого ключа одной из сторон обеспечивает аутентификацию ключа для этой стороны. Можно гарантировать, что только владелец соответствующего закрытого ключа сможет вычислить сеансовый ключ. Однако подтверждение факта получение ключа (выполнение целей G1 и G8) не является частью протокола.
Взаимодействие участников в протоколе Эль-Гамаля
  1. Алиса и Боб выбирают общие параметры $p$ и $g$, где $p$ — большое простое число, а $g$ — примитивный элемент поля $\mathbb{Z}_p^*$.
    Боб создаёт пару из закрытого и открытого ключей $b$ и $K_B$:

    $\begin{array}{l} b: 2 \leq b \leq p - 1, \\ K_B = g^b \bmod p. \end{array}$


    Открытый ключ $K_B$ находится в общем открытом доступе для всех сторон. Криптоаналитик не может подменить его — подмена будет заметна.
  2. Алиса выбирает секрет $x$ и вычисляет сеансовый ключ $K$

    $ K = K_B^{x} = g^{bx} \bmod p. $

    $ Alice \to \left\{ g^x \bmod p \right\} \to Bob$

  3. Боб вычисляет сеансовый ключ

    $ K = (g^x)^{b} = g^{bx} \bmod p. $


Протокол не обеспечивает гарантию выбора нового сессионного ключа в каждом сеансе протокола (G10), а использование «мастер»-ключа $K_B$ для передачи сеансового ключа позволяет злоумышленнику вычислить все сессионные ключи из прошлых сеансов при компрометации закрытого ключа $b$ (цель G9).

Протокол MTI/A(0)


В 1986 году Ц. Мацумото (Tsutomu Matsumoto), И. Такашима (Youichi Takashima) и Х. Имаи (Hideki Imai) предложили несколько алгоритмов, позже названных семейством протоколов MTI ([Matsumoto, Tsutomu, Imai 1986]). За счёт предварительного распространения открытых ключей обоих сторон они обеспечивали неявную аутентификацию ключа (цель G7). То есть сессионный ключ гарантированно мог получить только владельцы соответствующих открытых ключей. Мы рассмотрим одного из представителей данного семейства — протокол MTI/A(0).

Предварительно стороны договорились об общих параметрах системы $p$ и $g$, где $p$ — большое простое число, а $g$ — примитивный элемент поля $\mathbb{Z}_p^*$.

Взаимодействие участников в протоколе MTI/A(0)

Каждая из сторон (Алиса и Боб) сгенерировала пару из закрытого и открытого ключей:

$\begin{array}{ll} Alice: & ~ a, ~~ K_A = g^a \bmod p, \\ Bob: & ~ b, ~~ K_B = g^b \bmod p. \\ \end{array}$


  1. Алиса сгенерировала случайное число $R_A: ~ 2\leq R_A\leq p-1$
    $ Alice \to \left\{ g^{R_A} \bmod p \right\} \to Bob$
  2. Боб сгенерировал случайное число $R_B: ~ 2\leq R_B\leq p-1$
    Боб вычислил сеансовый ключ $K = (g^{R_A})^b \cdot K_A^{R_B} \bmod p$
    $ Bob \to \left\{ g^{R_B} \bmod p \right\} \to Alice$
  3. Алиса вычислила сеансовый ключ $K = (g^{R_B})^a \cdot K_B^{R_A} \bmod p$

Если открытые ключи $K_A$ и $K_B$ соответствуют своим закрытым ключам $a$ и $b$, то вычисленные участниками сессионные ключи совпадают:

$\begin{array}{lll} (g^{R_A})^b \cdot K_A^{R_B} \bmod p & = & g^{b R_A + a R_B} \bmod p, \\ (g^{R_B})^a \cdot K_B^{R_A} \bmod p & = & g^{a R_B + b R_A} \bmod p. \end{array}$


Из-за сложности задачи дискретного логарифмирования злоумышленник не сможет получить $a, R_A$ или $b, R_B$ из передаваемых сообщений, а предварительная публикация открытых ключей гарантирует, что сессионный ключ получат только легальные пользователи. Случайный выбор $R_A$ и $R_B$ гарантирует, что обе стороны могут быть уверены в создании нового сессионного ключа в каждом сеансе протокола.

Как и другие представители криптосистем-протоколов, MTI не разрабатывался с учётом возможности компрометации закрытых «мастер»-ключей $a$ и $b$ (цель G9).

Протокол Station-to-Station


Протокол STS (Station-to-Station, [Diffie, Oorschot, Wiener 1992]) предназначен для систем мобильной связи. Он использует идеи протокола Диффи—Хеллмана и криптосистемы RSA. Особенностью протокола является использование механизма электронной подписи для взаимной аутентификации сторон.

Предварительно стороны договорились об общих параметрах системы $p$ и $g$, где $p$ — большое простое число, а $g$ — примитивный элемент поля $\mathbb{Z}_p^*$.

Каждая из сторон $A$ и $B$ обладает долговременной парой ключей: закрытым ключом для расшифрования и создания электронной подписи $K_{\text{public}}$ и открытым ключом для шифрования и проверки подписи $K_{\text{public}}$.

$\begin{array}{ll} A: K_{A,\text{private}}, K_{A,\text{public}}: \forall M : & \text{Verify}_A ( M, S_A( M ) ) = true, \\ & D_A ( E_A( M ) ) = M, \\ B: K_{B,\text{private}}, K_{B,\text{public}}: \forall M : & \text{Verify}_B ( M, S_B( M ) ) = true, \\ & D_B ( E_B( M ) ) = M. \\ \end{array}$

Где $\text{Verify}_A(\dots)$ это функция проверки электронной подписи на открытом ключе $K_{A, \text{public}}$, а $D_A$ — функция расшифрования с использованием закрытого ключа $K_{A, \text{private}}$.

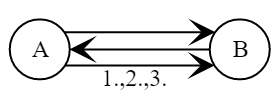
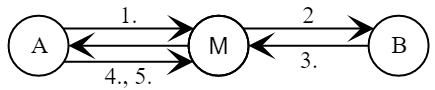
Протокол состоит из четырёх проходов, три из которых включают передачу сообщений ([Черёмушкин 2009]).

Взаимодействие участников в протоколе STS
  1. Алиса выбирает случайное число $R_A: 2 \leq R_A \leq p-1$.
    $Alice \to \left\{ A, m_A = g^{R_A} \bmod p \right\} \to Bob$
  2. Боб выбирает случайное число $R_B: 2 \leq R_B \leq p-1$.
    Боб вычисляет сессионный ключ $K = m_A^{R_B} \bmod p$.
    $Bob \to \left\{ B, A, m_B = g^{R_B} \bmod p, E_K( S_B ( m_A, m_B )) \right\} \to Alice$
  3. Алиса вычисляет сессионный ключ $K = m_B^{R_A} \bmod p$.
    Алиса проверяет подпись в сообщении $E_K( S_B ( m_A, m_B ))$.
    $Alice \to \left\{ A, B, E_K( S_A ( m_A, m_B ) ) \right\} \to Bob$
  4. Боб проверяет подпись в сообщении $E_K( S_A ( m_A, m_B ))$.

Протокол обеспечивает арантию формирования новых ключей (G10), но не совершенную прямую секретность (G9).

Как показала атака Лоу 1996 года ([Lowe 1996]), протокол не может гарантировать аутентификацию субъектов (цель G1), ключей (G7) и подтверждение владения сессионным ключом (G8). Хотя злоумышленник не может получить доступ к новому сессионному ключу, если протокол использовать только для аутентификации субъектов, Алиса может принять злоумышленника за Боба.

Взаимодействие участников в протоколе STS при атаке Лоу
  1. Алиса выбирает случайное число $R_A: 2 \leq R_A \leq p-1$.
    $Alice \to \left\{ A, m_A = g^{R_A} \bmod p \right\} \to Mellory~(Bob)$
  2. $Mellory \to \left\{ M, m_A \right\} \to Bob$
  3. Боб выбирает случайное число $R_B: 2 \leq R_B \leq p-1$.
    Боб вычисляет сессионный ключ $K = m_A^{R_B} \bmod p$.
    $Bob \to \left\{ B, M, m_B, E_K( S_B ( m_A, m_B )) \right\} \to Mellory$
  4. $Mellory~(Bob) \to \left\{ B, A, E_K( S_B ( m_A, m_B )) \right\} \to Alice$
  5. Алиса вычисляет сессионный ключ $K = m_B^{R_A} \bmod p$.
    Алиса проверяет подпись в сообщении $E_K( S_B ( m_A, m_B ))$.
    $Alice \to \left\{ A, B, E_K( S_A ( m_A, m_B ) ) \right\} \to Mellory~(Bob)$

После успешного завершения протокола Алиса уверена, что общается с Бобом.

Как и все остальные «криптосистемы-протоколы», протокол Station-to-Station основывается на некотором внешнем источнике информации об открытых ключах участников, не подвергая сомнению корректность и надёжность этого источника. Что, в общем случае, неверно. Если информация о ключах участников нужно получать извне при каждом сеансе протокола (например, если участников много, и запомнить ключи всех возможности нет), то канал получения открытых ключей будет основной целью активного криптоаналитика для рассмотренных протоколов. Как от этого защититься с использованием примитивов асимметричной криптографии — в следующем разделе.

Литература


  • [Diffie, Hellman 1976] Diffie W., Hellman M. E. New directions in cryptography // Information Theory, IEEE Transactions on. — 1976. — нояб. — т. 22, № 6. — с. 644—654. — ISSN 0018-9448. — DOI: 10.1109/TIT.1976.1055638.
  • [ElGamal, 1984] El Gamal T. A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms // Proceedings of CRYPTO 84 on Advances in Cryptology. — Santa Barbara, California, USA: Springer-Verlag New York, Inc., 1985. — с. 10—18. — ISBN 0-387-15658-5. — URL: dl.acm.org/citation.cfm?id=19478.19480.
  • [ElGamal, 1985] El Gamal T. A public key cryptosystem and a signature scheme based on discrete logarithms // IEEE Transactions on Information Theory. — 1985. — июль. — т. 31, № 4. — с. 469—472. — DOI: 10.1109/TIT.1985.1057074.
  • [Matsumoto, Tsutomu, Imai 1986] Matsumoto T., Takashima Y., Imai H. On seeking smart publickey-distribution systems // Trans. Inst. Electron. Commun. Eng. Jpn. Sect. E. т. 69. вып. 2. — 02.1986. — с. 99—106.
  • [Diffie, Oorschot, Wiener 1992] Diffie W., Van Oorschot P. C., Wiener M. J. Authentication
    and authenticated key exchanges // Designs, Codes and Cryptography. — 1992. — июнь. — т. 2, № 2. — с. 107—125. — ISSN 1573-7586. — DOI: 10.1007/BF00124891.
  • [Lowe 1996] Lowe G. Some new attacks upon security protocols // CSFW ’96 Proceedings of the 9th IEEE workshop on Computer Security Foundations. —Washington, DC, USA: IEEE Computer Society, 1996. — с. 162.
  • [Черёмушкин 2009] Черёмушкин А. В. Криптографические протоколы: основные свойства и уязвимости // Прикладная дискретная математика. — 2009. — нояб. — вып. 2. — с. 115—150. — URL: cyberleninka.ru/article/n/kriptograficheskieprotokoly-osnovnye-svoystva-i-uyazvimosti.pdf.

Послесловие
Автор будет благодарен за фактические и другие замечания к тексту.

Let's block ads! (Why?)

на Комментариев нет:
Ярлыки: ,
Подписаться на: Сообщения (Atom)