. Кроме этого, есть область 
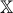, в которой генерируются начальные позиции частиц. В соответствии с планом работы GS, начинается все с генерации системы частиц 
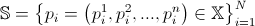, где 
— максимальное количество частиц в системе.Сила, действующая в момент времени 
на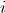 
-ю частицу со стороны 
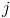-й, рассчитывается по формуле 
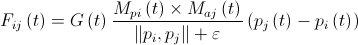, где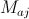 
— активная гравитационная масса 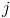-й частицы, 
— пассивная гравитационная масса 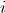-й частицы, 
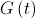— гравитационная постоянная в соответствующий момент времени, 
— малая константа, 
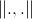— евклидово расстояние между частицами.
Чтобы алгоритм был не детерминированным, а стохастическим, в формулу расчета результирующей силы 
добавляются случайные величины 
(равномерно распределенные от нуля до единицы). Тогда результирующая сила равна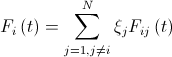 
.
Посчитаем ускорения и скорости: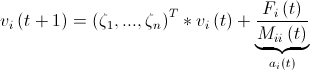 
, где 
— операция покомпонентного умножения векторов, 
— случайная величина, равномерно распределенная от нуля до единицы,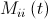 
— инертная масса 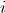-й частицы.
Остается пересчитать положение частиц. Сделать это очень просто: 
.
К текущему моменту осталось два вопроса: как изменяется гравитационная постоянная и как рассчитывать массы частиц. Значение гравитационной постоянной должно определяться монотонно убывающей функцией, зависящей от начального значений постоянной 
и момента времени , т.е.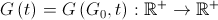 
.
Например, можно брать следующие функции:
Теперь можно приступить к заключительной части повествования: к пересчету масс. В простейшем случае все три массы (пассивная, активная и инерциальная) приравниваются:
. Тогда значение масс можно пересчитать по формуле: 
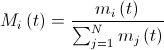, где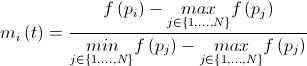 
.Конечно, можно рассчитывать массы исходя из их физического значения, тем не менее Рашеди об этом не говорит (и никто из авторов, которых я смог найти).
This entry passed through the Full-Text RSS service — if this is your content and you're reading it on someone else's site, please read the FAQ at fivefilters.org/content-only/faq.php#publishers. Five Filters recommends:
- Massacres That Matter - Part 1 - 'Responsibility To Protect' In Egypt, Libya And Syria
- Massacres That Matter - Part 2 - The Media Response On Egypt, Libya And Syria
- National demonstration: No attack on Syria - Saturday 31 August, 12 noon, Temple Place, London, UK
Комментариев нет:
Отправить комментарий