Введение
Numenta NuPIC — открытая реализация алгоритмов, моделирующих процессы запоминания информации человеком, происходящие в неокортексе. Исходные коды NuPIC на github
В двух словах, назначение NuPIC можно описать как «фиговина, выявляющая, запоминающая и прогнозирующая пространственные и временные закономерности в данных». Именно этим большую часть времени занимается человеческий мозг — запоминает, обобщает и прогнозирует. Очень хорошее описание этих процессов можно найти в книге Джеффа Хокинса «On Intelligence» (есть русский перевод книги под названием «Об интеллекте»).
На сайте Numenta есть подробный документ, детально описывающий алгоритмы и принципы работы, а также несколько видео.
Сборка и установка
Описана в readme файле в репозитории, поэтому детализировать не буду. Для работы, nupic потребуется python2.7 (или 2.6) с заголовочными файлами.
Параметры и структура модели
Ключевым понятием nupic является модель неокортекса (или просто — модель), представляющая собой набор клеток, обрабатывающих и запоминающих входные данные. В процессе обработки входных данных, клетки прогнозируют вероятное развитие событий, что автоматически формирует прогноз на будущее. Про то, как это делается, я расскажу в следующей статье, сейчас лишь общее описание самых необходимых вещей.
Модель состоит из нескольких процессов, поведение каждого из которых задается набором параметров.
Encoder
Входные данные проходят через encoder, преобразуясь в понятный модели вид. Каждая клетка воспринимает лишь бинарные данные, причем для работы, близкие по значению данные должны иметь похожее бинарное представление.
Например, на вход модели мы хотим подавать числа из интервала от 1 до 100 (скажем, текущую относительную влажность). Если просто взять бинарное представление чисел, что значения 7 и 8, расположены рядом, но бинарное их представление отличается очень сильно (0b0111 и 0b1000). Чтобы этого избежать, encoder преобразует числовые значения в набор единичных бит, сдвинутых пропорционально пропорционально значению. Например, для диапазона значений от 1 до 10 и трех единичных бит, получаем следующее представление:
- 1 -> 111000000000
- 2 -> 011100000000
- 3 -> 001110000000
- 7 -> 000000111000
- 10 -> 000000000111
Если на входе несколько значений, то их бинарные представления просто объединяются вместе.
Аналогично представляются значения с плавающей точкой и дискретный набор значений (true/false, и другие перечислимые типы).
Spatial Pooler
Основная задача SP — обеспечить активацию близкого набора клеток на похожий набор данных, добавляя в эту активацию элемент случайности. Подробное обсуждение как это делается выходит за рамки статьи интересующиеся могут подождать продолжения, либо обратиться к первоисточнику (whitepaper).
Temporal Pooler
Помимо определения похожих образов входных данных, NuPIC умеет различать контекст этих данных, анализируя их поток во времени. Достигается это за счет многослойности набора клеток (так называемые клеточные колонки), и подробное описание также выходит за намеченные рамки. Тут достаточно сказать, что без этого, система не отличала бы символ B в последовательности ABCABC от того же символа в CBACBA.
Практика: синус
Довольно теории, перейдем к практической стороне вопроса. Для начала возьмем простую функцию синуса, подадим на вход модели и посмотрим насколько хорошо она сможет ее понять и предсказать.
Полный код примера, разберем ключевые моменты.
Для создания модели по набору параметров, используется класс ModelFactory:
from nupic.frameworks.opf.modelfactory import ModelFactory
model = ModelFactory.create(model_params.MODEL_PARAMS)
model.enableInference({'predictedField': 'y'})
MODEL_PARAMS — это довольно развесистый dict с полным набором параметров модели. Все параметры нас сейчас не интересуют, но на некоторых стоит остановится.
'sensorParams': {
'encoders': {
'y': {
'fieldname': u'y',
'n': 100,
'name': u'y',
'type': 'ScalarEncoder',
'minval': -1.0,
'maxval': 1.0,
'w': 21
},
},
Здесь задаются параметры encodera, преобразующего значение синуса (в диапазоне от -1 до 1) в битовое представление. Значения minval и maxval определяют диапазон, значение n задает общее количество бит в результате, а w — количество единичных бит (оно почему-то должно быть нечетным). Таким образом, весь диапазон разделяется на 79 интервалов с шагом 0.025. Для проверки вполне достаточно.
Остальные параметры менять пока не нужно — их много, но значения по умолчанию вполне работают. Даже после прочтения witepaper и нескольких месяцев копания с кодом, точное назначение некоторых опций остается для меня загадкой.
Вызов метода enableInference у модели, указывает какой из входных параметров мы хотим прогнозировать (он может быть только один).
Подготовка закончена, можно накачивать модель данными. Делается это так:
res = model.run({'y': y})
В аргументы подается dict, в котором перечислены все входные значения. На выходе модель возвращает объект, содержащий в себекопию входных данных (как в оригинальном представлении, так и в закодированном), а также прогноз на следующий шаг. Больше всего нас интересует именно прогноз в поле inferences:
{'encodings': [array([ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 1., 1.,
1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32)],
'multiStepBestPredictions': {1: 0.2638645383168643},
'multiStepPredictions': {1: {0.17879642297981466: 0.0083312500347378464,
0.20791169081775931: 0.0083320832430621525,
0.224951054343865: 0.020831041503470333,
0.24192189559966773: 0.054163124704840825,
0.2638645383168643: 0.90834250051388887}},
Прогнозировать мы можем на несколько шагов сразу, поэтому в словаре multiStepPredictions ключом является количество шагов прогноза, а значением — другой словарь с прогнозом в ключе и вероятностью в значении. Для примера выше, модель предсказывает значение 0.26386 с вероятностью 90.83%, значение 0.2419 с вероятностью 5.4% и т.д.
Наиболее вероятный прогноз находится в поле multiStepBestPredictions.
Вооружившись всем этим знанием, пытаемся прогнозировать простой синус. Ниже показаны графики прогонов программы, с указанием параметров запуска. На верхнем графике синяя линия — оригинальный синус, зеленая — прогноз модели, сдвинутый на один шаг влево. На нижнем графике среднеквадратичная ошибка за 360 значений назад (полный период).
Вначале ошибка довольно велика, и прогнозируемое значение заметно отличается от оригинального значения (sin-predictor.py -s 100):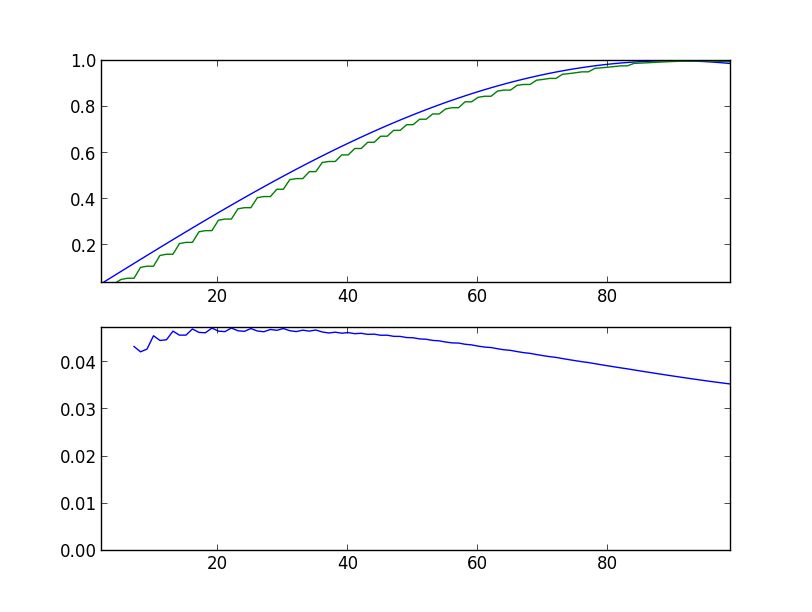
Через 1000 шагов: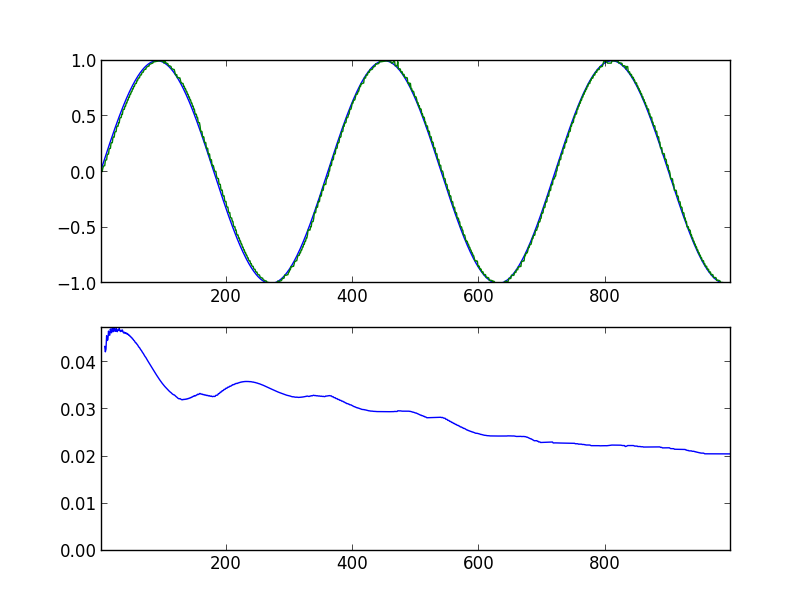
Прогресс налицо. Через 10000 шагов: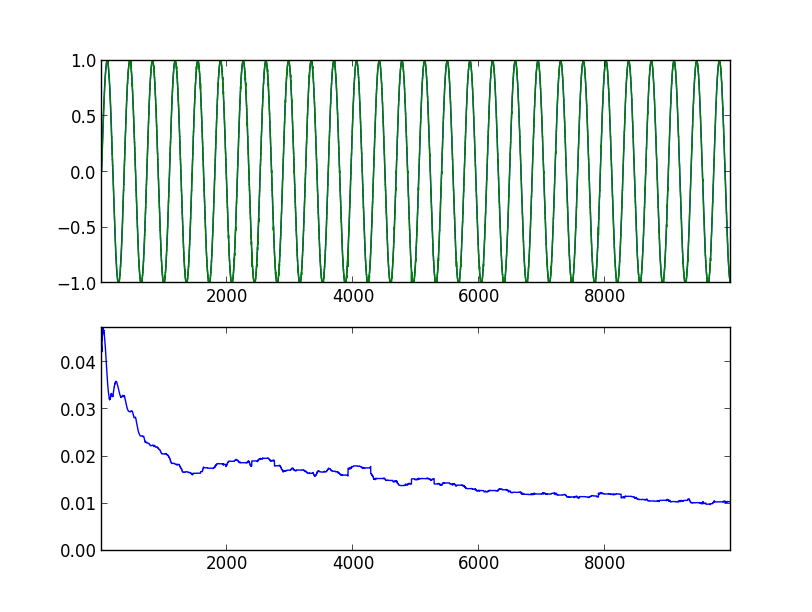
Через 10000 шагов, последние 360 значений: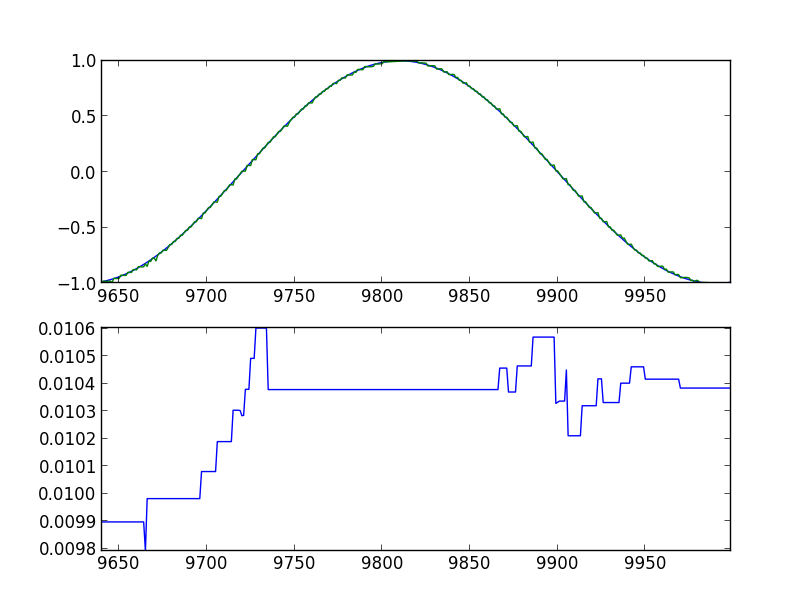
Видно, что модель определенно получила некоторые представления о том что от нее хотят.
Заключение
В этой статье я попытался дать самое общее представление о том как пользоваться NuPIC, не уходя в дебри деталей реализации. За кадром осталось много всего — структура сети, система визуализации cerebro, swarming, и т.п. Если будет время и интерес к теме, статьи можно продолжить.
This entry passed through the Full-Text RSS service — if this is your content and you're reading it on someone else's site, please read the FAQ at fivefilters.org/content-only/faq.php#publishers. Five Filters recommends:
- Massacres That Matter - Part 1 - 'Responsibility To Protect' In Egypt, Libya And Syria
- Massacres That Matter - Part 2 - The Media Response On Egypt, Libya And Syria
- National demonstration: No attack on Syria - Saturday 31 August, 12 noon, Temple Place, London, UK
Комментариев нет:
Отправить комментарий