
Древние греки — приверженцы концепций, имеющих строгий логический смысл — всячески избегали концепции бесконечности. Действительно, какое нам дело до бесконечного ряда чисел, если ни записать, ни представить его мы не можем.
В средние века логическую строгость отбросили ради математических результатов и разработали чрезвычайно эффективные алгоритмические методы, оперирующие в вычислениях бесконечностью.
В XX в. стала отчетливо проступать другая проблема. С бесконечностью мы можем разобраться при помощи одного символа (∞), но что делать с числами, которые меньше бесконечности, но при этом невообразимо огромны?
Мы вплотную подошли к числам, едва уступающим «уроборосу», но при этом все еще имеющим теоретическое и практическое значение. Вы, вероятно, могли слышать о числе Грэма, которое является верхней границей для решения определенной проблемы в теории Рамсея. Спустя 88 лет после появления теоремы Рамсея математики готовы отбросить старые методы и пойти еще дальше.
Добро пожаловать в кроличью нору без дна.
Вступление, в котором нужно вспомнить прошлое
В XVII в. математик и философ Блез Паскаль писал о своем страхе перед бесконечностью, о чувстве собственной незначительности при мысли о безбрежных просторах космоса. Интересно, что сказал бы Паскаль о числе Грэма, состоящем из башни чисел высотой от Земли до самой отдаленной звезды, в каждом числе которой прячется своя башня из чисел? Каждый изгиб числа в башне чисел, которая состоит из башни чисел, вмещает в себя башню других чисел — но даже с такой формулировкой мы и близко не подошли к открытию, сделанному Грэмом.
Истоки числа Грэма следует искать в 1928 г., когда молодой математик Фрэнк Рамсей во время работы над статьей о логике заметил удивительную вещь: полная неупорядоченность невозможна. Каждое достаточно большое множество чисел, точек или объектов обязательно содержит высокоупорядоченную структуру.
Догадка, которая была лишь небольшой частью работы о логике, положила начало совершенно новой области математики, называемой теорией Рамсея. Ее часто объясняют на примере вечеринки: предположим, вы хотите найти идеальный баланс между теми, кто знает друг друга, и незнакомцами. Вы рисуете карту отношений всех ваших друзей, связывая двух людей, если они являются друзьями, синей линией, и красной — если они не знакомы друг с другом. Тогда может получиться подобная иллюстрация:

Красота теории Рамсея заключается в том, что задачи в этой области всегда очень легко формулировать. Рассматривая пример с вечеринкой, очень интересно понять, какого количества людей достаточно для образования группы, в которой всегда окажется четверо людей либо знакомых, либо не знакомых друг с другом.
В группе из 17 точек, изображенных на рисунке выше, невозможно найти четыре точки, для которых сеть соединяющих их ребер была бы целиком красной или синей. Поэтому требуется более 17 человек, чтобы среди них обязательно оказалось четверо людей, знакомых или не знакомых друг с другом. На самом деле в группе из 18 человек всегда найдутся либо четверо знакомых, либо четверо не знакомых друг с другом.
Возьмем любое звездное скопление. В нем всегда можно найти группу, которая с очень большой точностью образует какую-нибудь заданную конфигурацию — прямую линию, прямоугольник, ковш.
Математики стараются вычислить, сколь велико должно быть множество звезд, чисел или каких-либо объектов, чтобы можно было гарантировать существование определенной желаемой подструктуры. На решение таких задач часто уходят десятилетия.
Теория Рамсея также имеет большое практическое значение — от организации хорошей вечеринки до построения более совершенных сетей коммуникации и систем передачи и поиска информации. На самом деле очень сложно представить, для каких целей могут послужить многие методы, разработанные для решения задач в теории Рамсея — это самый передовой край математики.
Как и почему Грэм пришел к своему числу
Американский математик Рональд Льюис Грэм (родился в 1935 г.) внес значительный вклад в дискретную математику. Грэм — личность разносторонняя. В свое время он даже был президентом международной ассоциации жонглеров, но прославился исключительно за счет большого положительного целого числа, которое служит верхней границей конкретной проблемы в теории Рамсея.
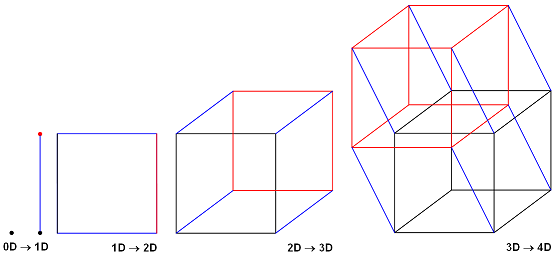
N-мерный куб всегда содержит 2n вершин. Несмотря на их размерность, n-мерные кубы — это просто графы, вершины которых связаны ребрами
Любой n-мерный куб мы можем превратить в полный граф, просто соединив все вершины. Остальные ребра, сформированные таким образом, находятся внутри или на одной из граней. Представим, что эти края имеют два цвета — красный и синий. Таким образом, Грэм сформулировал интересный вопрос, лежащий в плоскости классической теории Рамсея: при каком минимальном значении N двухцветного k-мерного куба каждая такая раскраска обязательно содержит раскрашенный в один цвет полный подграф с четырьмя вершинами, каждая из которых лежит в одной плоскости?

Полный граф на трехмерном кубе с раскраской ребер в два цвета
В 1971 г. Рональд Грэм и Брюс Ли Ротшильд доказали, что у этой задачи есть решение, и оно представляет собой число, которое больше 6 (нижняя граница), и меньше некоего N. Нижняя граница впоследствии была повышена до 13, а верхняя граница получила название малого числа Грэма. Малое число Грэма меньше числа, попавшего в Книгу рекордов Гиннесса, но это все равно невообразимо огромное число.
В общем-то, задача Грэма не звучит как нечто сверхъестественное — ее может понять и пятиклассник. Но на простые вопросы иногда очень трудно получить ответы. Если решение меньше, чем число Грэма, которое мы знаем, то каков же ответ? Число Грэма, как и некоторые другие большие числа, просто говорит нам, что у некоторой задачи в принципе есть решение, и это решение можно найти. Оптимизировав решение задачи, мы можем сдвинуть число Грэма ближе к 1, и двигать его до тех пор, пока не найдем реального решения.
Как число стало легендой
Итак, Рональд Грэм написал профессиональную математическую работу по теории Рамсея, которая привлекла внимание журналиста Мартина Гарднера. Именно Гарднер ипоспособствовал попаданию числа Грэма в Книгу рекордов Гиннесса, после чего число привлекло внимание широкой общественности.
Проблема, которую Грэм пытался решить, на самом деле была лишь одним конкретным примером применения теории Рамсея. Дальнейшие исследования в этой теории дали математикам бóльшие числа, чем даже число Грэма. Эти числа не являются точным решением проблем, а выступают верхней границей.
Возможно, лучшие теоремы в теории Рамсея могут резко сократить верхние границы, что приведет к исчезновению огромного количества супербольших чисел. Такое, к примеру, случилось с числом Скьюза: в 1987 г. его определили как 8,185·10370, а через 30 лет оказалось, что оно лежит между 1019 и 1,3971672·10316.
Чем же очаровал Грэм людей? Красотой и наглядностью.
Чтобы оперировать гигантскими числами, Грэм использовал быстрорастущие функции. Многие из этих функций знакомы всем — сложение, умножение и возведение в степень. Математики создали новые функции, которые масштабируются намного быстрее.
Для записи числа Грэм использовал стрелочную нотацию Кнута — расширение возведения в степень. Точно так же, как возведение в степень является повторным умножением и обозначается одной стрелкой, направленной вверх, две стрелки вверх обозначают итерационное возведение в степень, три стрелки — повторное итерационное возведение в степень и т.д.
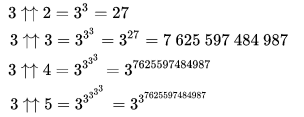
Или так:
3↑↑5 = 3↑3↑3↑3↑3 = три в степени три в степени 7 625 597 484 987.
Математики поняли, что, имея дело с большими числами, требуется каждый раз использовать новый оператор, который должен быть мощнее предыдущего. ↑↑ — следующий оператором от ↑, так же как ↑ — следующий оператор от умножения, и точно так же, как умножение — это один оператор от сложения. Таким образом, увеличение количества последовательных стрелок увеличивает способность работать с большими числами.
Если добавить еще одну стрелку, то скорость формирования новых чисел значительно возрастет:
3 ↑↑↑ 3 дает нам башню из степеней троек высотой в 7 трлн чисел.
Четыре стрелочки даст число, записать которое будет уже очень трудно. Обратимся к примеру из замечательной статьи «Число Грэма на пальцах»:
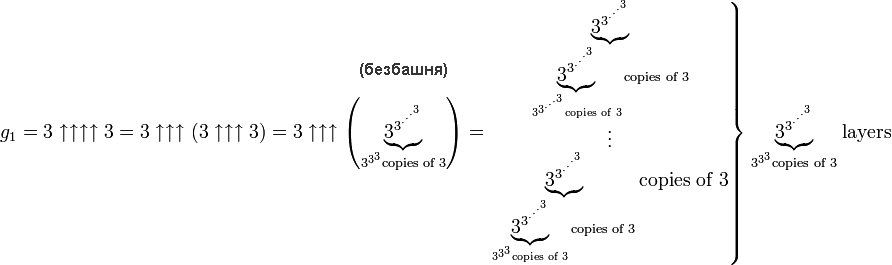
А вот оригинальная иллюстрация, которую Гарднер использовал для объяснения числа Грэма:
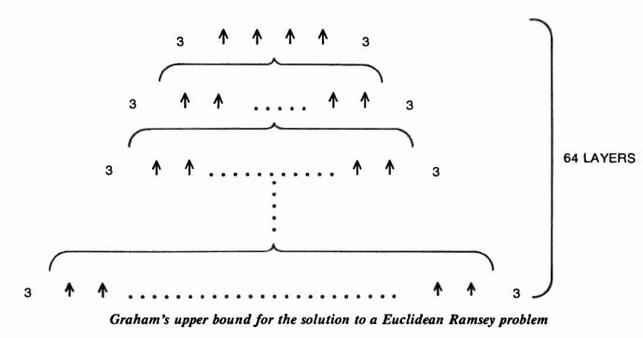
Самый верхний уровень равен 3 ↑↑↑↑ 3. Формулу вы видели выше. Под ним находится слой, в котором число стрелочек равно 3 ↑↑↑↑ 3. Далее идет слой, в котором число стрелочек равно числу стрелочек в предыдущем слое. И так до 64-го слоя.
Красота этого выражения в том, что если вы захотите превзойти число Грэма и напишите «супербольшое число = число Грэма + 1», то в математических масштабах ничего не изменится. Все равно что залезть на вершину Эвереста и прыгать на ней — Эверест все равно останется самой высокой горой, на вершину которой вы можете взобраться.
Но где-то в Солнечной системе есть и Олимп, не так ли?
Нотация Бауэрса: начало кроличьей норы
Дальнейшая работа с теорией Рамсея математиков Джозефа Краскала и Харви Фридмана привела к числу TREE(3), у которого даже самая нижняя граница решения является сверхогромной, не говоря о верхней.
Если число Грэма мы хотя бы можем записать, то число TREE(3) невозможно поместить в рамки нотации Кнута. Судите сами:
TREE (3) = … > AA(187196)(4), где даже A2(4) больше, чем число атомов во Вселенной, ведь А — функция Аккермана, которая определяется рекурсивно для неотрицательных целых чисел m и n следующим образом:
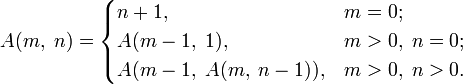
Используя функцию Аккермана, можно очень легко записать число Грэма ≈ A64(4).
Математики вычислили, что у TREE(3) есть теоретическая граница, которую можно записать с помощью массивной нотации, предложенной в 2002 г. Джонатаном Бауэрсом. В массивной нотации существует пять правил:
- {а} = а и {a,b} = ab
- {а,b,c,…,n,1} = {а,b,c,…,n}
- {а,1,b,c,…,n} = a
- {а,b,1,…,1,c,d…,n} = {а,a,a,…,{а,b – 1,1…,1,c,d…,n},c – 1,d…,n}
- Если правила 1—4 не применяются, то {а,b,c,d…,n} = {а,{а,b – 1,c,d…,n},c – 1,d…,n}
В простейшем случае массивная нотация при массиве из двух элементов выглядит следующим образом: {10,100} = 10100 или же 10 ↑ 100.
Функция возрастает невероятно быстро. Массив из трех элементов {10,100,2} в стрелочной нотации Кнута будет иметь следующий вид: 10 ↑2 100.
Тройные массивы Бауэрса полностью идентичны тройным цепочкам обозначения Конвея (еще один метод записи — соединенные горизонтальными стрелками (цепочками) числа, растут быстрее нотации Кнута):
{3,3,3} = 3 → 3 → 3 = 3 ^ (3 ^ (3 ^ (3 ^… 7 625 597 484 987 раз… ^ 3) ^ 3) ^ 3)
Массив из четырех элементов (например {10,100,1,2}) уже больше самого числа Грэма — благодаря хитрости, придуманной Бауэрсом: на четвертом элементе он «оптимизирует» формулу, как раньше мы оптимизировали умножение и возведение в степень, только теперь математик занимается удвоением скобок:
{3,3,1,2} = 3 1 3 = 3 {3 {3} 3} 3 = {3, 3, {3, 3, 3}}.
Более подробный разбор этой операции вы можете найти в статье «Bird’s Linear Array Notation».
При этом «самое больше число, использованное в серьезном математическом доказательстве», ограничено между {3,65,1,2} и {3,66,1,2}. Речь сейчас идет только о линейных массивах, а ведь они могут быть и гипермерными. В принципе массив Бауэрса из четырех элементов способен вместить в себя всю нотацию Конвея, а гипермерные массивы (на иллюстрации выше) уже становятся математической гиперигрой.
Красота математики в том, что мы можем работать с данными, которые даже представить невозможно. Любую сложную задачу можно облегчить до невероятно простых значений. Возможно, ответы на некоторые вопросы мы никогда не найдем, но методы, использованные для их решения, могут пригодиться в других областях знаний. Сама проработка этих методов построения иерархий по скорости роста функций совершенствует многие разделы математики.
Бауэрс сделал удачную попытку ответить на вопрос, как с помощью иерархии приемов расширить возможности формальной системы. Фактически мы записываем не само число иносказательным образом, а способ когда-нибудь прийти к этому числу хотя бы в теории.
Нотации Бауэрса стали отличной возможностью подобраться к пониманию функции TREE. Конечно, определить величину TREE(3) мы не можем, но с помощью итерационного «улучшения» нотации, проведенного английским математиком Крисом Бердом, удалось выяснить, что TREE(3) > {3,6,3[1[1¬1,2]2]2}.
TREE(3)
TREE — быстрорастущая функция в теории графов, разработанная математиком Харви Фридманом.
Предположим, что мы имеем последовательность k-пронумерованных деревьев T1, T2,… со следующими свойствами:
- каждое дерево Ti имеет не более i вершин;
- ни одно дерево невложимо гомеоморфно в любое дерево, следующее за ним в последовательности.
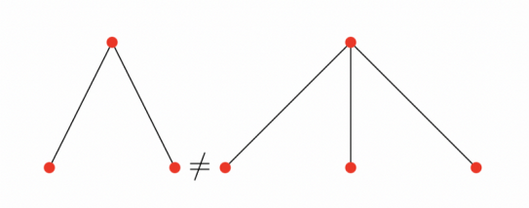
Ti < Tj, то есть Ti невложимо в Tj
Такая последовательность не может быть бесконечной. Первым эту теорию выдвинул Джозеф Крускал в 1960 г. Харви Фридман расширил теорию, задав вопрос: учитывая k, какова максимальная длина такой последовательности деревьев?
Эта максимальная длина является функцией от k, называемой TREE(k).
TREE(1) = 1. Первое дерево — уникальное дерево с одной вершиной, помеченной 1. Это дерево, очевидно, вложимо в любое другое дерево, поэтому мы закончили на 1:

TREE(2) = 3. Первое дерево может быть только единственным одновершинным деревом, помеченным 1 или 2. Обозначим его 1 (красный). Тогда никакие другие деревья не могут использовать метку 1 — все вершины должны быть помечены меткой 2 (синий). Второе дерево может быть либо единственным одновершинным деревом, либо уникальным двухвершинным:
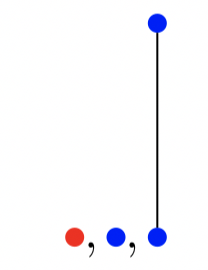
Вот мы и подошли к самому интересному: TREE(3) = … — это непостижимо великое число. Вероятно, способ определить его масштабы никогда не будет изобретен, так как это на порядок выше человеческих возможностей. Посмотрим, как выглядит начало числа:
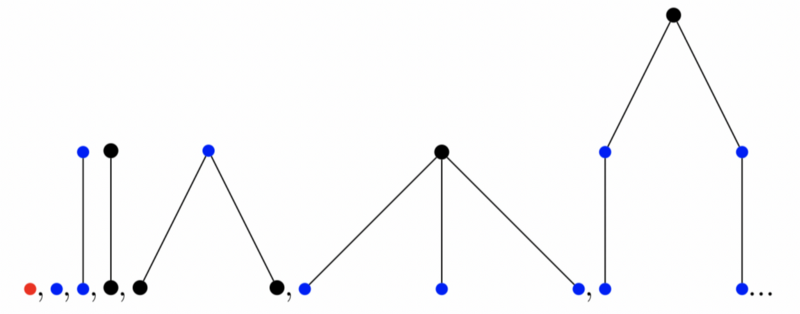
TREE(3) начинается таким образом и продолжается ОЧЕНЬ долгое время.
Бездна: SCG(n)
Математики не могли остановиться на TREE(3) и пошли дальше. Нет, не к TREE(4). Функция TREE(n) более слабая по сравнению с Buchholz гидрами и Subcubic Graph Numbers. Subcubic Graph Function — SCG(n) — дает величайший результат.
Здесь нужно сделать небольшое отступление: с 1983 до 2004 г. математики Нил Робертсон и Пол Д. Сеймур в 500-страничном исследовании разработали теорию о том, что любое наследуемое свойство графов характеризуется конечным числом запрещенных подграфов. Теорема Робертсона-Сеймура распространяет эти результаты на произвольные замкнутые по минорам семейства графов. Теорема указывает, что множество тороидальных графов имеет конечное препятствующее множество, но не дает ни одного такого множества. Полный набор запрещенных миноров для тороидальных графов остается неизвестным и содержит по меньшей мере 16 тыс. графов.
Простой субкубический граф представляет собой конечный простой граф, в котором каждая вершина имеет степень не более трех. Предположим, у нас есть последовательность простых субкубических графов G1, G2, ... — такая, что каждый граф Gi имеет не более i + k вершин (для некоторого целого k) и гомеоморфно вложим в Gj.
Теорема Робертсона-Сеймура доказывает, что подкубические графы (простые или нет) вполне обоснованы гомеоморфной вложимостью, подразумевая, что такая последовательность не может быть бесконечной. Таким образом, для каждого значения k существует последовательность с максимальной длиной. Функция SSCG(k) обозначает эту длину для простых субкубических графов. Функция SCG(k) обозначает эту длину для (общих) субкубических графов.
Последовательность SSCG начинается с SSCG(0) = 2, SSCG(1) = 5, но затем быстро растет. SSCG(2) = 3 × 23 × 295 – 8 ≈ 103,5775 × 1028.
SSCG(3) не только больше, чем TREE(3), он намного больше, чем TREE (TREE (... TREE(3) ...)), где общая глубина вложенности формулы является уровнем TREE(3) функции TREE. Нет качественного различия между асимптотическими темпами роста SSCG и SCG. Ясно, что SCG(n) ≥ SSCG(n), но также можно сказать, что SSCG(4n + 3) ≥ SCG(n).
В бесконечность и дальше: BIG FOOT и другие числа

Математики и сейчас разрабатывают теории, которые могут использоваться для создания «самого-самого» числа. «Король» цифрового ряда часто меняется, но закончить сегодняшний обзор хочется на прекрасном числе BIG FOOT. Пусть оно больше, чем TREE(3) и SSCG(3) вместе взятые, но уже не считается САМЫМ большим. Однако механика его создания не потеряла актуальности и используется для исследования новых величайших чисел.
Прежде чем переходить к легендарному снежному человеку, познакомимся с теорией чисел Райо. Число Райо — это большое число, названное в честь математика Агустина Райо, победившего на «дуэли больших чисел» в 2007 г. со следующим определением: «Самое маленькое число, большее, чем любое конечное число, которое может быть определено выражением на языке первого порядка теории множеств с использованием менее, чем гугола (10100) символов».
BIG FOOT является аналогом числа Райо — его определение почти идентично. BIG FOOT расширяет теорию множеств первого порядка, используя уникальную область дискурса, называемую oodleverse, с использованием языка, называемого first-orderoodletheory (FOOT), и обобщая теорию множеств n-го порядка сколь угодно большого n.
Пусть FOOT(n) обозначает наибольшее натуральное число, однозначно определяемое в языке FOOT не более чем в n символах. BIG FOOT определяется как FOOT10(10100), где FOOTa(n) — это FOOT(n) (рекурсия).
BIG FOOT таким образом равен
FOOT(FOOT(FOOT(FOOT(FOOT(FOOT(FOOT(FOOT(FOOT(FOOT(10100))))))))))
Поиски конечного числа продолжаются. Будет ли оно когда-нибудь найдено?
Блез Паскаль так описал экзистенциальный ужас, охватывающий его при мысли о безграничности мира: «Вечная тишина этого бесконечного пространства пугает меня». Числа дают нам возможность установить рамки понимания и границы дозволенного, взять под контроль страх уробороса. Они — наше реликтовое излучение, возможность подойти к метафорическому краю мира. Но, как в космосе нельзя долететь до такого места, где будет висеть табличка «конец Вселенной», так и в математике невозможно достичь последнего рубежа. Впрочем, это нам еще предстоит проверить.
P.S. Автор не является профессиональным математиком и надеется, что не допустил грубых ошибок в статье. Если вы заметили неточность — сообщите. Также приветствуются комментарии, расширяющие изложенный материал.
Источники:
Комментариев нет:
Отправить комментарий