Статьи из цикла:
Введение
Задача этой статьи — помочь вам быстро познакомиться с основными принципами работы квантовых вентилей и понять, как эти вентили объединяются в цепи, наглядно представляющие квантовые алгоритмы (некоторые из них мы обсудим в последующих публикациях).
Для вашего удобства я опубликую сводную информацию обо всех важнейших вентилях, элементах схем и т. п. из статей этой серии в виде шпаргалки (чтобы вам не пришлось долго искать нужные сведения). В моих будущих статьях она будет называться «Квантовые вычисления: краткая справка».
Основы: квантовые состояния
Начнем с основ — с обозначений некоторых распространенных квантовых состояний, которыми мы будем впоследствии манипулировать:
Все они являются чистыми однокубитными состояниями, поэтому их можно представить в виде точек на сфере Блоха:
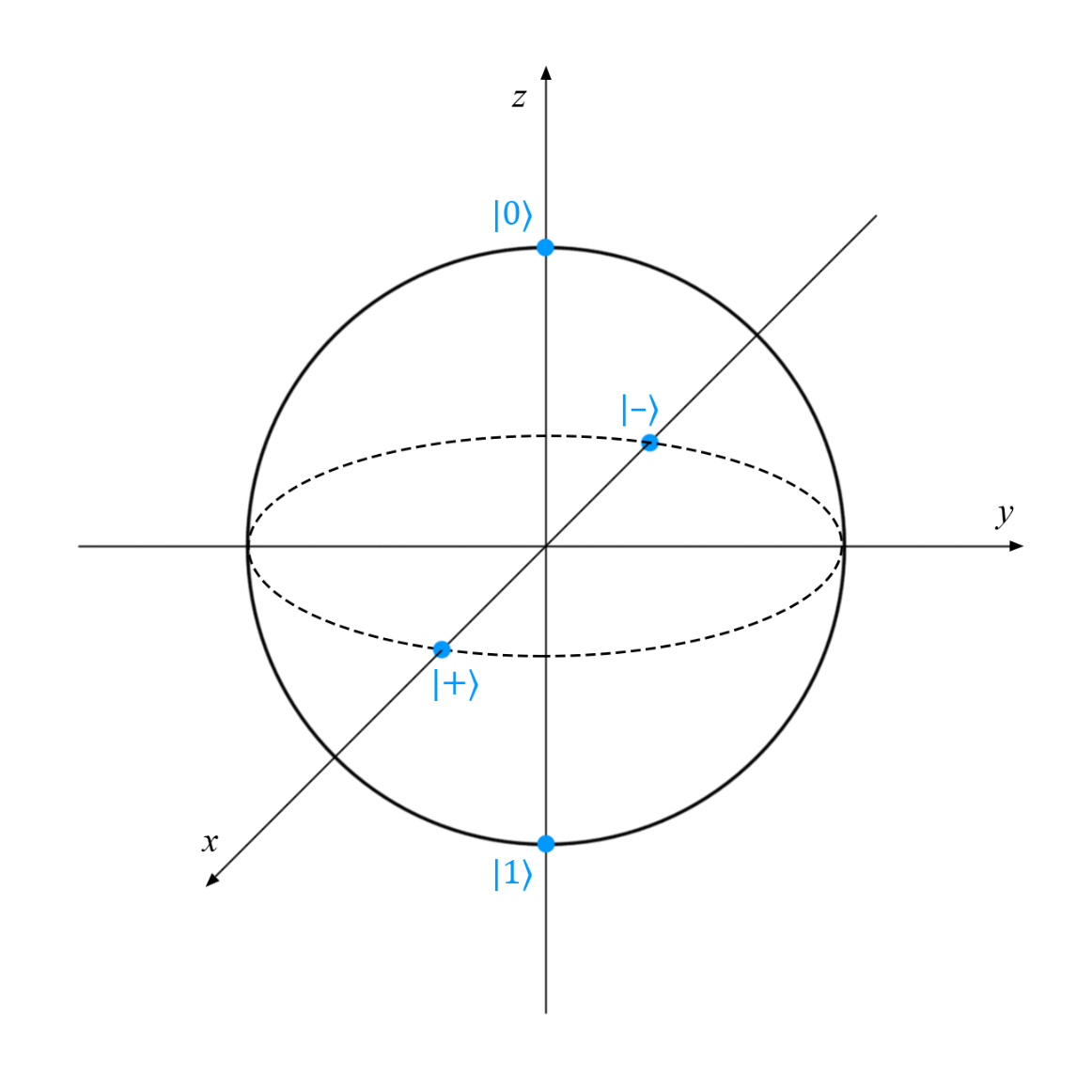
Теперь — четыре состояния Белла (их еще называют парами ЭПР, в честь Эйнштейна, Подольского и Розена — именно они являются авторами идей, которые впоследствии развил Белл). Это простейшие примеры квантовой запутанности двух кубитов:
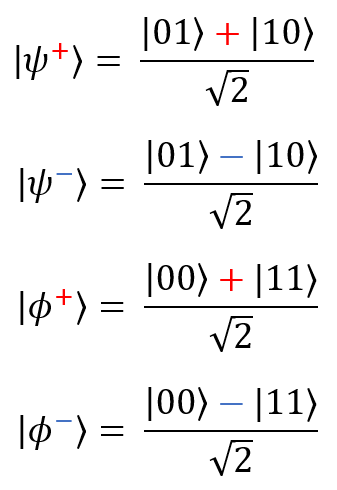
И наконец, мы будем использовать так называемые состояния ГХЦ (Гринберга — Хорна — Цайлингера). Вот их общая форма (для n кубитов) и простейшая форма (для трех кубитов):
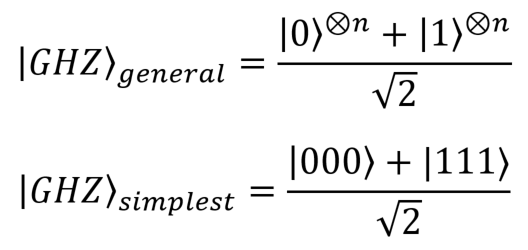
Состояния Белла и состояния ГХЦ очень важны, потому что их поведение кардинально отличается от предсказаний классической теории из-за уровня запутанности в таких системах (этот принцип «максимальной запутанности» будет рассмотрен в одной из последующих публикаций).
Основы: радианы
Углы поворота в теории квантовых вычислений измеряются в радианах. Полная окружность (360°) соответствует 2π радиан. Углы измеряются против часовой стрелки. Ниже показаны величины важнейших углов в градусах и в радианах.
Основы: диаграммы квантовых цепей
Перед тем как углубляться в изучение квантовых вентилей, следует изучить основы построения диаграмм квантовых цепей (это не займет много времени):
- Время на квантовой диаграмме движется слева направо.
- Каждому кубиту соответствует одиночная горизонтальная линия.
- Вентили обычно обозначаются квадратами. Тип вентиля обозначается буквами или другими символами в этом квадрате (бывают и исключения из этого правила. Обычно это кубитные вентили, у которых есть классические аналоги (пример — вентиль NOT)).
- Некоторым вентилям может соответствовать несколько элементов диаграммы (пример — вентиль NOT).
- В результате измерения кубита все суперпозиции коллапсируют, квантовые свойства кубита исчезают, и он превращается в обычный бит. Поэтому можно считать, что измерительный элемент (показанный ниже) принимает на вход кубит и выдает классический бит. Этой операции в языке Q# соответствует команда Measure(bases: Pauli[], qubits: Qubit[]) или M(qubit: Qubit) по основанию Z.
Вот обозначения важнейших элементов:
Более подробная информация приводится в документации здесь и в книге М. Нильсена и И. Чанг «Квантовая информация и квантовые вычисления».
Однокубитные вентили
Однокубитные вентили закономерно являются самыми простыми, поэтому мы начнем с них. Операцию, выполняемую любым однокубитным вентилем, можно представить как поворот вектора, характеризующего состояние кубита, в другую точку сферы Блоха (см. ниже).
Самые элементарные однокубитные вентили — это вентили Паули X, Y и Z:
Вентиль Y ожидаемо соответствует повороту вектора вокруг оси y на π радиан. В результате такой операции вектор |0〉 превращается в i|1〉, а |1〉 — в -i|0〉.
Вентиль Z представляет собой особый случай вентиля фазового сдвига 
(см. ниже) при фи = π = 180°. Он соответствует повороту вектора вокруг оси z на π радиан. Вектор |0〉 он оставляет без изменений, а |1〉 преобразует в -|1〉.
Ниже работа этих преобразований проиллюстрирована с помощью сферы Блоха (ось вращения в каждом случае выделена красным; на картинку можно нажать, чтобы увеличить ее):
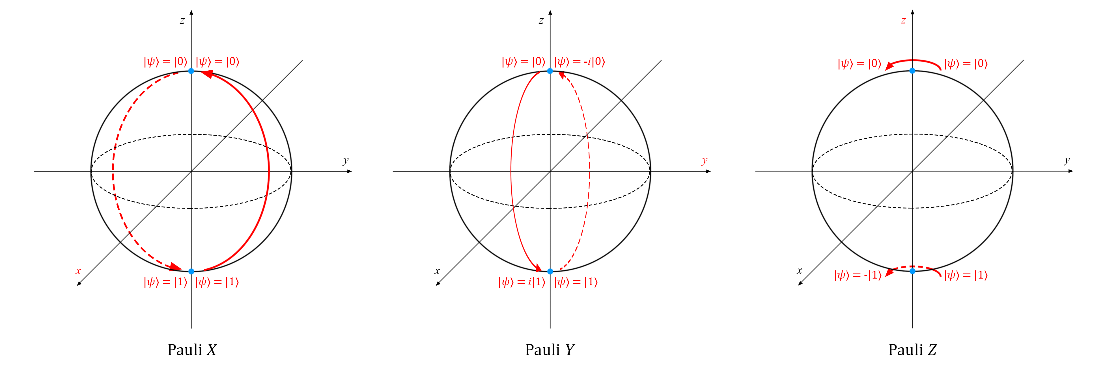
Важно отметить, что после двукратного применения одного и того же вентиля Паули к кубиту он перейдет в исходное состояние (потому что после поворота вектора на 2π радиан или 360° вокруг любой оси он перейдет в начальное положение). Как следствие,
Поскольку 
и т. д.,
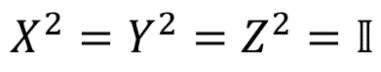
Здесь II — обозначение единичной матрицы: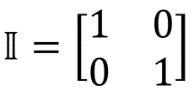 
. Единичной называется матрица, результат умножения которой на произвольную матрицу M (II) равен матрице M: MII = IIM = M. Единичная матрица соответствует квантовой операции, которая не меняет квантовое состояние. На сфере Блоха это выглядит так:
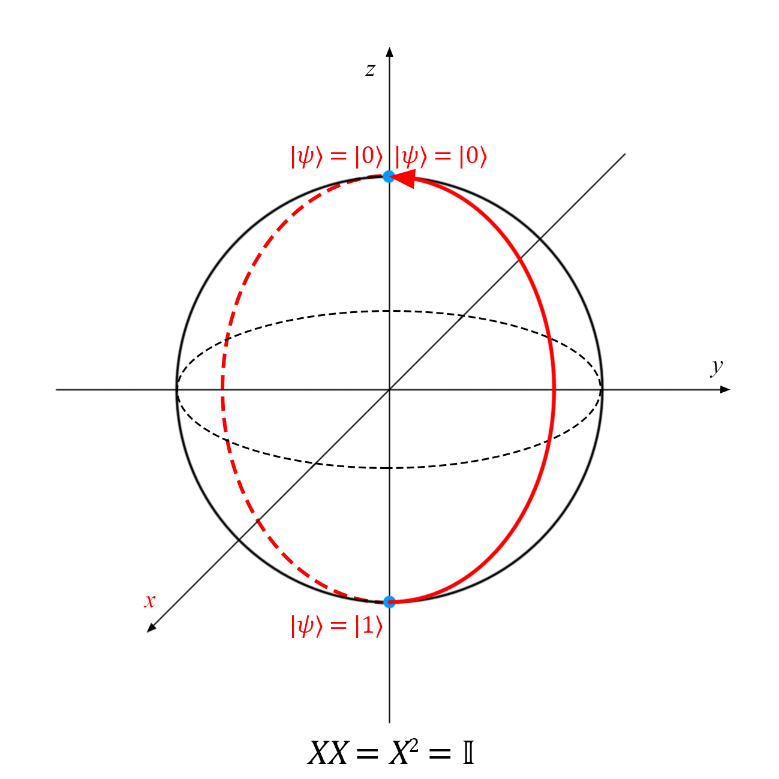
Ввиду этого отношения говорят, что матрица Паули в квадрате равна единичной матрице.
Ниже приводится описание еще нескольких важных однокубитных вентилей.
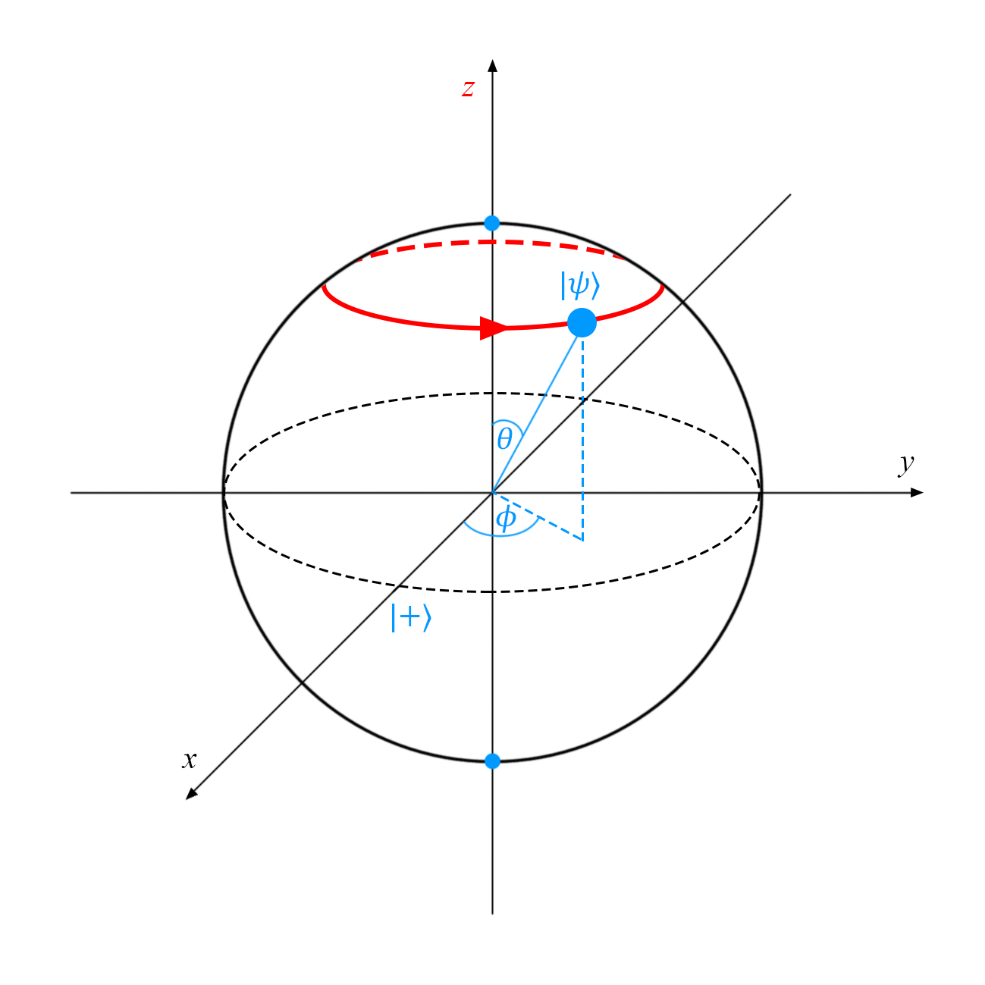
Вентиль фазового перехода представляет достаточно общую операцию, у которой есть множество полезных применений. Самые распространенные его вариации — вентили сдвига фазы на π/4, π/8 и Паули-вентиль Z, для которых параметр фи равен π/2, π/4 и π соответственно. Пример фазового сдвига 
на сфере Блоха:
Многокубитные вентили
Многокубитные вентили выполняют операции над двумя или более кубитами. Один из простейших примеров — вентиль SWAP:
Вентиль SWAP меняет местами два входных кубита. Например, SWAP|0〉|1〉 = |1〉|0〉, а SWAP|0〉|0〉 = |0〉|0〉 (полная таблица истинности приводится в шпаргалке по цепям).
Еще один класс многокубитных вентилей — так называемые управляемые вентили. На вход любого управляемого вентиля подается по меньшей мере один управляющий и один управляемый кубит, причем вентиль выполнит операцию над управляемым кубитом только в том случае, если управляющий кубит находится в определенном состоянии.
Вентили, которые выполняют операцию при управляющем кубите |1〉, обозначаются заполненным кругом на проводе управляющего кубита. Вентили, которые выполняют операцию при управляющем кубите, равном |0〉, обозначаются пустой окружностью, как показано ниже.
Для того чтобы составить матрицу любого управляющего вентиля, нужно дописать единичную матрицу в левом верхнем углу матрицы нужного вентиля, а все остальные ячейки заполнить нулями. Вот пример:
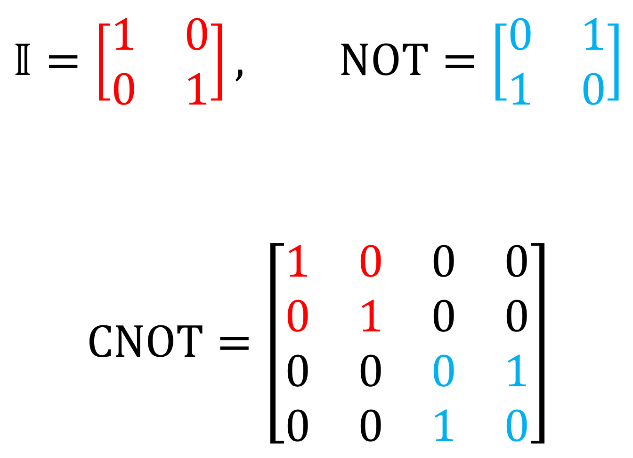
Обычные вентили в Q# можно преобразовать в управляющие с помощью ключевого слова Controlled, как описано здесь (в разделе «Controlled» в самом низу страницы). Например, вентиль CNOT (напомним, что вентиль NOT эквивалентен X-вентилю Паули) можно получить командой
(Controlled X)([control], (target))
где [control] — массив входных управляющих кубитов.
Ниже описаны другие распространенные управляемые вентили (мы выделили единичную матрицу красным, а матрицу исходного вентиля — синим, как выше):
Универсальные наборы
Как мы уже упоминали в предыдущей публикации, вне зависимости от того, с помощью какой физической системы мы имитируем квантовый компьютер, должна иметься возможность реализовать «универсальный набор» вентилей. Это значит, что любая допустимая вычислительная операция в нашей системе должна быть преобразуема к конечной последовательности известных вентилей. Вот пример такого универсального набора: вентиль Адамара, вентиль фазового сдвига, вентиль CNOT и вентиль π⁄8.
Свойство универсальности гораздо интереснее, чем может показаться на первый взгляд. Если в квантовом компьютере существует универсальный набор вентилей, то любое преобразование, которое допускают законы квантовой физики, можно реализовать с его помощью. Это значит, что с помощью универсального набора можно не просто выполнить любую квантовую программу, а имитировать любое физическое явление. Поэтому свойство универсальности позволяет использовать квантовые компьютеры для моделирования молекул, сверхпроводников и любых странных и прекрасных квантовых систем. Эта особенность квантовых компьютеров позволяет имитировать физические явления, что в перспективе позволит квантовым системам превзойти потенциал самых мощных суперкомпьютеров. Уже не скучно, правда?
Нас ждет еще много интересного!
С помощью этих (и некоторых других) важнейших вентилей уже можно создавать полнофункциональные квантовые цепи! В следующей публикации я расскажу, как с помощью этих новоприобретенных знаний можно реализовать квантовое преобразование Фурье — очень важную операцию, у которой есть огромное множество практических применений.
Комментариев нет:
Отправить комментарий