[Перевод] Ричард Хэмминг: Глава 15. Цифровые фильтры — 2

«Цель этого курса — подготовить вас к вашему техническому будущему.»

Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2372 в закладки, 375k прочтений)?

Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводи, ведь мужик дело говорит.

Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»

Мы уже перевели 17 (из 30) глав. И ведем работу над изданием «в бумаге».

Глава 15. Цифровые фильтры — 2

(За перевод спасибо Пахомову Андрею, который откликнулся на мой призыв в «предыдущей главе».) Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru

Когда цифровые фильтры только появились, они рассматривались как разновидность классических аналоговых фильтров; люди не рассматривали их как-что то принципиально новое и отличающееся от уже существующего. Точно такая же ошибка была распространена во время появления первых компьютеров. Мне неустанно твердили, что компьютер — это всего лишь быстрый калькулятор, и все, что может посчитать машина, может посчитать и человек. Это утверждение просто игнорирует различия в скорости, точности, надежности и стоимости между ручным и машинным трудом. Обычно, изменение какой-либо величины на порядок (в 10 раз) приводит к фундаментальным изменениям, а компьютеры во много-много раз быстрее, чем ручные вычисления. Те, кто утверждал, что нет никакой разницы, так и не сделали ничего значимого для развития компьютеров. Те же, кто внес значительный вклад, видели в компьютерах что-то новое, что-то, что следует оценивать совсем другим образом, а не просто как те же самые старые калькуляторы, только может быть чуть-чуть более быстрые.
Это общая, бесконечно повторяемая ошибка. Люди всегда хотят думать что новое — это что-то очень похожее на старое. Им нравится оставлять свои ум в зоне комфорта, так же, как и тело – таким образом они ограждают самих себя от возможности сделать любой значимый вклад в новых отраслях, которые возникают у них прямо под носом. Не все, что называется новым, является таким на самом деле, и в некоторых случаях трудно определить, является ли что-то по-настоящему новым. Тем не менее, общая установка «Здесь нет ничего нового» является глупой. Когда что-то называется новым, не спешите думать, что это просто улучшение чего-то старого – это может быть отличная возможность для вас сделать что-то значительное. Но опять-таки, в этом на самом деле может не быть ничего нового.

Первый цифровой фильтр, который я использовал во времена примитивных компьютеров, выполнял сначала трехкратное сглаживание, а потом пятикратное. Вспоминая формулу сглаживания, передаточная характеристика при трехкратном сглаживании определяется как

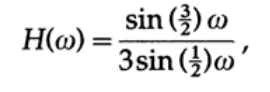
и может быть легко нарисована (рисунок 15.I). Передаточная характеристика в случае пятикратного сглаживания выглядит точно так же, только 3/2 заменяется на 5/2, и тоже может быть легко нарисована (рисунок 15.I). Для двух последовательных фильтров общая передаточная характеристика – это, очевидно, произведение их передаточных характеристик (каждый умножает входной сигнал – собственную функцию — на передаточную характеристику для соответствующей частоты).Вы увидите три нуля на интервале, а конечное значение будет равно 1/15. Дальнейшее исследование покажет вам, что верхняя половина частот была довольно хорошо отфильтрована простой компьютерной программой, которая посчитала сумму трех чисел, затем сумму 5-ти чисел и – это распространенная компьютерная практика переносить все операции деления в конец и заменять одним умножением – умножила результат на 1/15.

Сейчас вам наверное стало любопытно, как именно цифровой фильтр убирает определенные частоты из массива чисел – даже те студенты, которые прошли курс по цифровым фильтрам, могут не до конца понимать как это работает.

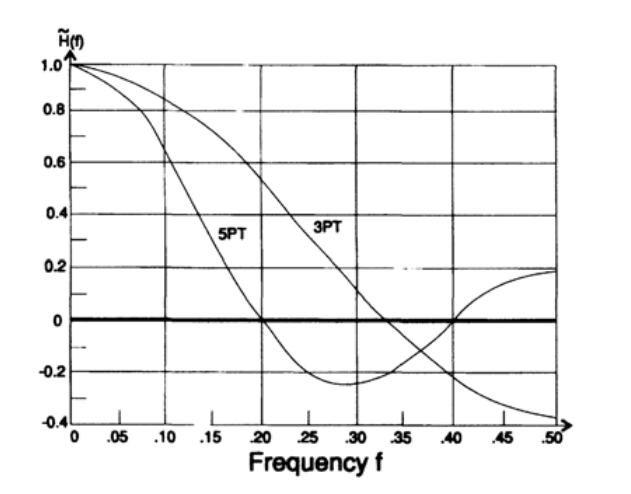
Рисунок 15.I.

Поэтому, я предлагаю вам синтезировать простой фильтр всего лишь с 2 коэффициентами — именно поэтому я могу наложить ровно два ограничения на передаточную функцию. В теории мы используем циклическую частоту, но на практике мы пользуемся частотой. Эти две величины связаны между собой следующим образом:

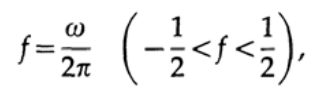
Сформулируем ограничения для нашего фильтра следующим образом: пусть для частоты f=1/6 значение передаточной характеристики фильтра будет равно 1 (эта частота должна проходить через фильтр без изменений), а для частоты f=1/3 значение передаточной характеристики должно быть равно нулю.

Мой простой фильтр выглядит следующим образом

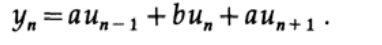
где a и b – параметры, значения которых мы попробуем определить.

Подставив в собственную функцию exp(2pifn) мы получим передаточную характеристику.

Подставим n=0 для удобства и получим следующую систему уравнений:

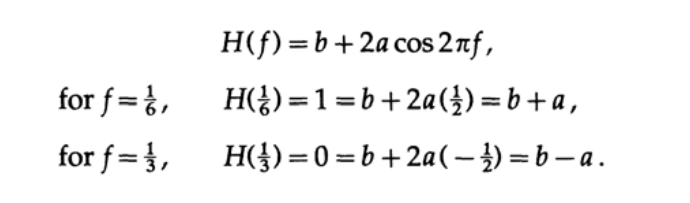
Данная система уравнений имеет решение a=b=1/2, а искомый сглаживающий фильтр это простое выражение

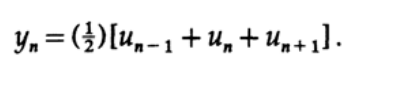
Другими словами, значение на выходе фильтра равно сумме трех последовательных значений на входе фильтра, деленной на три. Значение на выходе фильтра располагается напротив центрального значения входных данных.

Давайте подадим какие-нибудь тестовые данные на вход фильтра. В качестве сигнала передаваемого с частотой 1/6 мы будем использовать значения функции косинус такой же частоты, взятые через одинаковые промежутки времени (n =0, 1, 2, … ). Аналогичным образом смоделируем значения сигнала на частоте 1/3. Значение сигнала, подаваемого на вход фильтра в определенный момент времени, будет равно сумме значений этих сигналов в этот же момент времени.

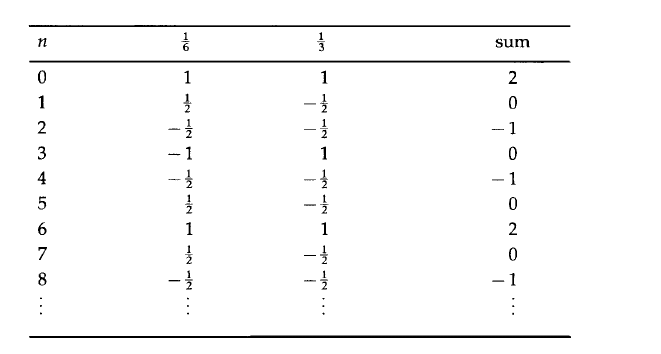
А теперь давайте пропустим этот сигнал через наш фильтр. Согласно полученной формуле фильтра, мы будем брать сумму трех последовательных чисел в колонке и делить ее на 2. Проделывая эту операцию над первой колонкой вы увидите, что каждый раз когда фильтр смещается на одну строчку в таблице вниз, он воспроизводит функцию, поданную на вход (умноженную на 1). Пропустите через фильтр вторую колонку, и вы увидите, что значение на выходе всегда равно нулю, или значению входной функции умноженной на собственное значение 0. Фильтрация третьей колонки, которая является суммой первых двух, должна пропустить первую частоту и остановить вторую. То есть после фильтрации третьей колонки вы получите первую колонку. Вы можете попробовать подать на вход сигнал с частотой равной нулю. В этом случае вы вы должно получить ровно 3/2 для каждого значения. Если вы попробуете частоту f=1/4, вы должны получить значения на входе, умноженные на ½ (значение передаточной характеристики для f=1/2).

Вы только что увидели цифровой фильтр в действии. Фильтр раскладывает входной сигнал на все его составные частоты, умножает каждую частоту на соответствующие ей собственное значение (передаточную характеристику), а затем суммирует их вместе, что бы получить значение на выходе. Это все делает одна простая линейная формула фильтра!
Давайте вернемся к проблеме синтеза фильтра. Часто мы хотим получить передаточную характеристику с резким спадом между частотами которые она передает неизменными (с собственным значением 1) и частотами которые она останавливает ( с собственным значением 0). Как вы знаете, такая функция с разрывом может быть разложена в ряд Фурье, однако этот ряд будет содержать бесконечное число членов. Несмотря на это, у нас есть ограниченное число таких членов, если мы хотим получить практически реализуемый фильтр; 2k+1 членов в сглаживающем фильтре позволяют получить только k+1 свободных коэффициентов, таким образом только k+1 обычных условий может быть наложено на соответствующую сумму косинусов.

Если мы просто разложим желаемую передаточную функцию в ряд косинусов, а потом уменьшим количество членов в нем, то мы получим аппроксимацию передаточной характеристики методом наименьших квадратов. Но в точках разрыва аппроксимация методом наименьших квадратов приводит не к тем результатам, которых вы можете ожидать.
Для того, чтобы понять что мы увидим в точках разрыва, мы должны исследовать эффект Гиббса. Для начала вспомним теорему: если ряд непрерывных функций равномерно сходится на отрезке, то сумма ряда является непрерывной на этом отрезке. Но ведь функция, которую мы аппроксимируем не является непрерывной – у нее есть скачок (разрыв) в точке разделения полосы пропускания и полосы заграждения. Не имеет значения, как много членов ряда мы будем использовать. Поскольку здесь не может быть равномерного схождения, мы можем ожидать увидеть значительный всплеск в окрестностях особой точки (точки разрыва). С увеличением числа членов рядов, величина всплеска не будет стремиться к нулю.

Вот еще одна байка. Майкельсон, известный благодаря эксперименту Майкельсона-Морли, построил аналоговое устройство, позволяющее определять коэффициенты разложения в ряд Фурье вплоть до 75 члена. Это устройство также позволяло перейти и от коэффициентов к функции. Когда Майкельсон восстановил функцию по коэффициентам ряда Фурье, он обнаружил всплеск и спросил у местных математиков почему это происходит.

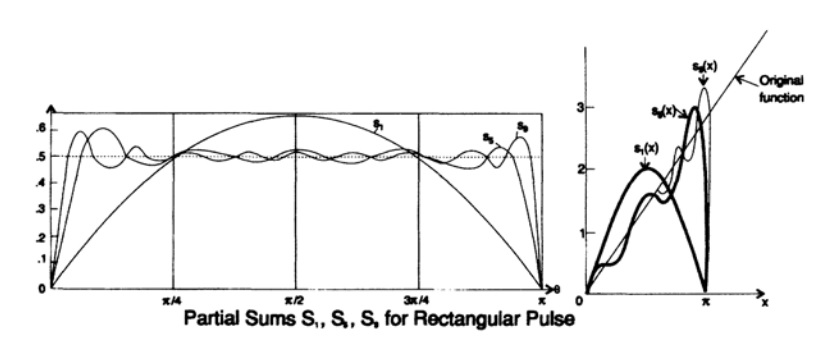
График 15.2

Все они сказали, что причина в его оборудовании – и это при том, что он был широко известен как педантичный экспериментатор. И только Гиббс, из Йельского университета, прислушался и изучил вопрос. Самый простой и прямолинейный подход заключается в том, чтобы разложить обычную функцию с разрывом, скажем в ряд Фурье с конечным числом членов, собрать исходную функцию заново и найти точку первого максимума и значение функции в этой точке.

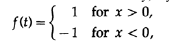
На графике 15.2 можно обнаружить всплеск на 0.0849, или всплеск в 8,949%, в пределе при количестве членов ряда Фурье стремящемся к бесконечности. Многие люди имели возможность открыть (на самом деле переоткрыть) эффект Гиббса, но именно Гиббс приложил усилие. Это еще одно подтверждение того, что я постоянно твержу – вокруг нас полно возможностей, и лишь немногие люди их реализуют. Как говорил Пастер, «Фортуна улыбается только тем, кто к этому готов ». В этот раз прославился человек, который оказался готов услышать первоклассного учёного и помочь ему решить его проблему.

Я отметил, что этот эффект был открыт заново. Именно так. В учебнике Коши 1850-ого года мы можем найти два противоречащих друг другу высказывания: (1) сходящиеся ряды непрерывных функций сходятся к непрерывной функции и (2) разложение в ряд Фурье функции с разрывами. Некоторые люди разобрались в вопросе и обнаружили, что необходимо ввести понятие равномерной сходимости. Именно так, эффекта Гиббса проявляется при разложении в ряд любых непрерывных функций, а не только для рядов Фурье. Этот факт был известен отдельным людям, но не нашел широко применения. В общем случае, при разложении в ряд ортогональных функций, размер всплеска зависит от того, где именно расположен разрыв раскладываемой функции. Это и отличает функции Фурье от других ортогональных функций, для разложения Фурье величина всплеска не зависит от того, где расположен разрыв.

Следует напомнить вам еще одно свойство рядов Фурье. Если функция существует, тогда коэффициенты уменьшаются как 1/n. Если функция непрерывна (значения с двух концов эстремума одинаковые и существует производная в этой точке, то коэффициенты уменьшаются как 1/n². Если первая производная непрерывная, а вторая производная существует, тогда они уменьшаются как 1/n³. Таким образом, скорость сходимости ряда определяется функцией расположенной в вдоль оси действительных чисел – что не является справедливым для рядов Тейлора, чья сходимость определяется особыми точками, которые могу лежат в комплексной плоскости.

А теперь вернёмся к дизайну нашего цифрового сглаживающего фильтра, используя преобразование Фурье, чтобы получить первые члены ряда. Как мы видим, аппроксимация методом наименьших квадратов имеет проблемы в особых точках – омерзительные всплески в передаточной функции состоящей из конечного числа членов, при этом не имеет значения как много членов ряда мы будем использовать.

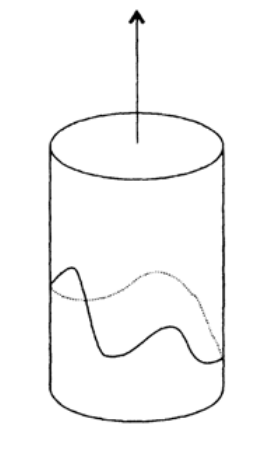
Рисунок 15.3

Для начала, рассмотрим окно Ланцоша (его еще называют «прямоугольным окном» или «прямоугольной функцией»), которое позволяет убрать всплеск. Ланцош рассуждал следующим образом: «если усреднить значение выходной функции на интервале длиной, равной периоду функции с наивысшей частотой, присутствующей в выходном сигнале, то это позволит сильно уменьшить звон». Чтобы рассмотреть это подробнее, возьмем первых N гармоник разложения в ряд Фурье и возьмем интеграл на симметричном интервале вокруг точки t длиной 1/N от всего интервала. Запишем интеграл для усреднения как

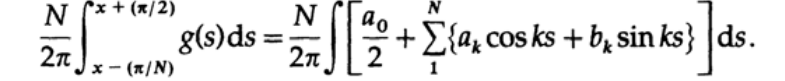
А теперь возьмем интеграл:

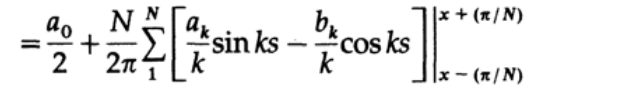
применим формулу разницы синусов и косинусов для границ интервала интегрирования:

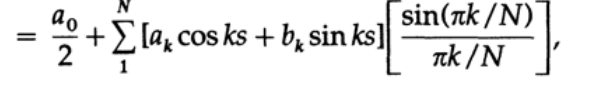
И получим первоначальные коэффициенты, умноженные на так называемые сигма-множители:

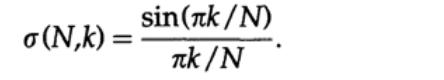
Рассмотрение последовательности таких чисел как функцию от k (N фиксировано и равно количеству взятых гармоник разложения в ряд Фурье) показывает, что для k=1 сигма множитель равен единицы, а с увеличением k сигма множители уменьшаются до нуля при k=N. То есть они являются еще одним примером оконной функции. Результатом применения окна Ланцоша является уменьшение всплеска до 0.01189 ( в 7 раз) и первого минимума до 0.00473 (в 10 раз), что является существенным, но не полным уменьшением эффекта Гиббса.

Но вернемся к моим приключениям в этой области. Я знал, как и вы, что в точках разрыва, разложение в ряд Фурье с конечным числом членов, равно среднему значению двух пределов взятых слева и справа от точки разрыва. Рассуждая о конечном, дискретном случае, я сделал вывод, что вместо того, чтобы брать единицу в полосе пропускания и ноль в полосе затухания, следует использовать ½ в качестве промежуточного значения.

И вот, передаточная характеристика стала выглядеть как

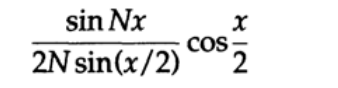
и теперь имеет дополнительный множитель (снова возвращаясь к частотной нотации)

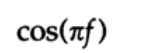
N+1 в синус членах ряда перешло в N, так же как и знаменатель N+1 перешел в N. Очевидно, эта передаточная характеристика для фильтра низких частот лучше чем у Ланцоша, потому что она затухает на частоте Найквиста и дополнительно гасит все вышележащие частоты. Я просмотрел книги по тригонометрическим рядам и только в одной из них – двухтомнике Зигмунда, — я нашел упоминание о таком ряде: там он назывался модифицированным рядом. Вовсе необязательно, что если бы я потратил больше времени на изучение теории, то я бы получил выдающий результат. Получив такую модификацию разложения в ряд самостоятельно, я естественным образом продолжил размышлять о дальнейших изменениях коэффициентов ряда Фурье (мне еще предстояло раобраться какие именно коэффициенты и каким образом нужно изменить), я мог получить лучший результат. Вкратце, я более четко понял что такое «оконные функции» и медленно подходил к более детальному исследованию их возможностей.

Существует еще третий подход к явлению Гиббса через объединение рядов Фурье. Пусть g(x) будет (у нас есть веская причина использовать нейтральную переменную x в данном случае):

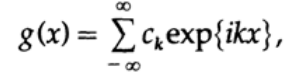
а другая функция будет

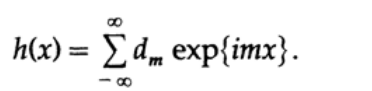
Сумма и разность g(x) и h(x) очевидно будут равны соответствующим рядам с суммой и разностью коэффициентов.

С произведением дело обстоит иначе. Очевидно, мы снова получим сумму экспонент, а определив n=k+m мы получим указанные коэффициенты:

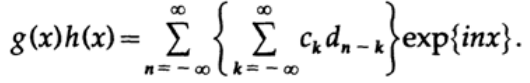
Коэффициент при exp{inx}, который является суммой членов, называется свёрткой первоначальных массивов коэффициентов.

В случае, когда в массиве c_k только несколько коэффициентов не равны нулю, возьмем например сучай с симметрией относительно 0, мы получим следующее выражение для коэффициента:

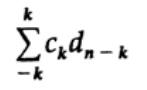
А это и есть первоначальное определение цифрового фильтра! Таким образом, фильтр – это свёртка двух массивов, которая в свою очередь является просто умножением соответствующих функций. Умножение с одной стороны равенства и свертка с другой.

В качестве примера использования этого наблюдения на практике, представим довольно распространенный случай: имеется бесконечный массив данных, но мы можем записать только конечное количество значений (например включение и выключение телескопа в процессе наблюдения за звездами). Такая функция u_n наблюдается через прямоугольное окно, где все значения за пределами 2N+1 равны нулю. Иными словами в моменты наблюдения оконная функция равна 1, а в остальное время 0.

Когда мы попробуем посчитать разложение в ряд Фурье исходного массива по записанным значениям, мы должны посчитать свертку коэффициентов исходного массива и оконной функции:

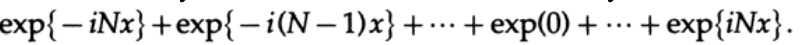
Как правило, мы хотим получить окно площадью в единицу, поэтому мы должны разделить на (2N+1). Полученный массив – это геометрическая прогрессия с первым членом exp{-iNx} и знаменателем прогрессии exp{ix}.

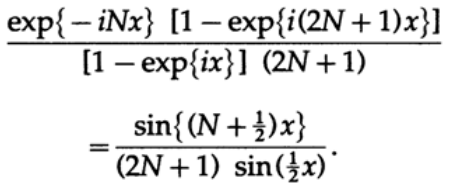
При x=0, значение выражения равно 1, в иных случаях значение выражения быстро колеблется благодаря синусу в числителе и медленно затухает благодаря увеличению значения синуса в знаменателе (x принадлежит интервалу (-π, +π). Таким образом мы получили типичную дифракционную картину оптики.

В случае непрерывного до дискретизации сигнала, ситуация складывается аналогичным образом, только прямоугольное окно, через которое мы наблюдаем сигнал, имеет преобразование общего вида (игнорируя все подробности):

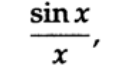
а его свертка со ступенчатой функцией (разрывом), приведет к появлению эффекта Гиббса (рисунок 15.II). Таким образом мы увидели всплески, обусловленные эффектом Гиббса, в другом свете.

Некоторые достаточно сложные тригонометрические преобразования убедят вас, что и дискретизация функции с последующим ограничением интервала наблюдения, и ограничение интервала наблюдения с последующей дискретизацией приведут вас к одному и тому же результату. Теория вам скажет то же самое.

Простое изменение двух внешних коэффициентов дискретного окна Ланцоша с 1 на ½ приводит к лучшей оконной функции. Окно Ланцоша изменяет все коэффициенты сигма-множителями, но его форма имеет углы по краям, а это означает, что из-за периодичности функции сушествует два разрыва в первой производной – следовательно и медленную сходимость. Если мы порассуждаем об использовании приподнятого косинуса

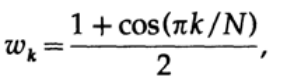
в качестве весовых коэффициентов при членах разложения в ряд Фурье, то мы получим что-то похожее на оконную функцию Ланцоша, только более гладкую, что приведет к более быстрой сходимости.

Выписав это в экспоненциальной форме мы обнаружим что весовые коэффициенты при экспонентах равны:

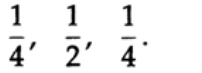
Мы только что получили окно Ханна. Сглаживание во временной области при помощи этих коэффициентов эквивалентно умножению в частотной области. На самом деле, я переоткрыл окно Ханна в самом начале работы над спектрами мощности, а позже Джон Тьюки обнаружил, что Ханн использовал его применительно к экономике намного-много раньше. Исследование того, что делает эта оконная функция с сигналом, показывает, что сигнал быстро затухает, но при этом имеет боковые лепестки, через которые попадает часть спектра.

Тогда мы имели дело со спектром, который имел ярко выраженную линию, и смотря на другие части спектра через окно Ханна, можно было обнаружить что боковые лепестки могли пропускать много энергии. Окно Хэмминга было разработано для того, чтобы сделать максимум боковых лепестков минимумом. Эта оконная функция позволила держать под контролем одну ярко выраженную линию в спектре, но ценой намного больших средне-квадратичных утечек
Если называть оконную функцию Ханна «приподнятым косинусом» с весовыми коэффициентами

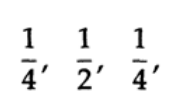
то окно Хэмминга – это «приподнятый косинус на платформе» (рисунок 15.IV), с весами

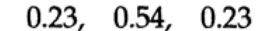
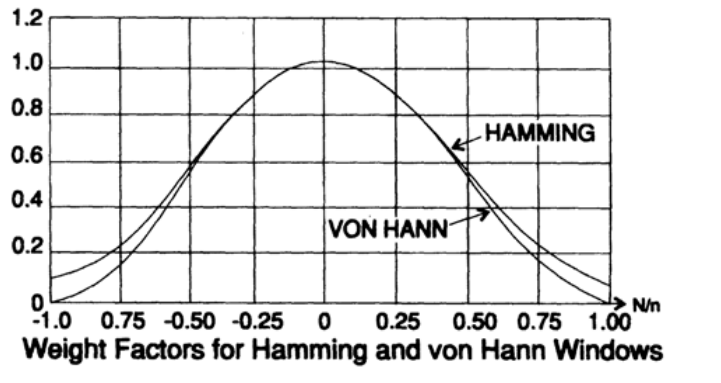
Рисунок 15.4

На самом деле веса зависят от N, длины массива данных, но во многих случаях используются несколько этих постоянных. Оконная функция Хэмминга стала популярной благодаря атмосфере загадочности вокруг своих необычных коэффициентов, хотя она была спроектирована для того чтобы решать одну конкретную задачу и не является универсальным решением всех проблем. В большинстве случае использование оконной функции Ханна предпочтительнее. В литературе описано, может быть, сотня различных оконных функций, каждая со своими достоинствами, но при этом ни одна из них не имеет всех преимуществ, которые вам хотелось бы видеть.

Чтобы посвятить вас во все тонкости той истории, я расскажу вам еще одну историю. Я имел привычку поддразнивать Джона Тьюки: «Ты известен только тогда когда, твое имя пишется с маленькой буквы, как ватт, ампер, вольт, иногда фурье, и тому подобное». Когда Тьюки впервые написал свою работу по спектрам мощности, он позвонил мне из Принстона и спросил, может ли он использовать мое имя в названии окна Хэмминга. После некоторых протестов, я все-таки согласился на его предложение. Книга вышла с именем «Хэмминг»! Это же я!

В некотором роде, именно ваши друзья, цитируя вас и ссылаясь на вас, делают вас известными. Таким образом вам платят за оказанную помощь, и поэтому я призываю вас помогать другим, когда они пробуют справится со своими задачами. Они могут вовремя доверить вам часть работы, и это может оказаться лучше, чем пробовать добиться этого самостоятельно. Сейчас кооперация – это основа сложных проектов. Дни одиночек отходят быстро. Работа в команде занимает все более и более значимое место, и поэтому обучение работе в команде, поиск мест где вы можете помочь другим – это хорошая идея. В любом случае удовольствие от работы с хорошими людьми над важными задачами приносит больше удовлетворения чем полученная по итогу известность. И наоборот, выбор себе важной задачи означает что руководство будет готово обеспечить вам любую помощь, которая вам может понадобиться.

За долгие годы работы в Лабораториях Белла, я был очень осторожен в публикации свои результатов, и не допускал ситуаций, которые бы выставляли меня вором чужих идей. Наоборот, я позволял другим публиковать свои работы, и если они хотели указать меня соавтором – отлично, я не против! Командная работа подразумевает тщательное внимание к другим людям и их вкладу, ведь они могут видеть его совсем в другом свете!

Продолжение следует...

Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru

Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)

Содержание книги и переведенные главы

1. Intro to The Art of Doing Science and Engineering: Learning to Learn (March 28, 1995) (в работе)Перевод: Глава 1
2. «Foundations of the Digital (Discrete) Revolution» (March 30, 1995) Глава 2. Основы цифровой (дискретной) революции
3. «History of Computers — Hardware» (March 31, 1995) Глава 3. История компьютеров — железо
4. «History of Computers — Software» (April 4, 1995) Глава 4. История компьютеров — Софт
5. «History of Computers — Applications» (April 6, 1995) Глава 5. История компьютеров — практическое применение
6. «Artificial Intelligence — Part I» (April 7, 1995) (в работе)
7. «Artificial Intelligence — Part II» (April 11, 1995) (в работе)
8. «Artificial Intelligence III» (April 13, 1995) Глава 8. Искуственный интеллект-III
9. «n-Dimensional Space» (April 14, 1995) Глава 9. N-мерное пространство
10. «Coding Theory — The Representation of Information, Part I» (April 18, 1995) (в работе)
11. «Coding Theory — The Representation of Information, Part II» (April 20, 1995)
12. «Error-Correcting Codes» (April 21, 1995) (в работе)
13. «Information Theory» (April 25, 1995) (в работе, Горгуров Алексей)
14. «Digital Filters, Part I» (April 27, 1995) Глава 14. Цифровые фильтры — 1
15. «Digital Filters, Part II» (April 28, 1995) Глава 15. Цифровые фильтры — 2
16. «Digital Filters, Part III» (May 2, 1995)
17. «Digital Filters, Part IV» (May 4, 1995)
18. «Simulation, Part I» (May 5, 1995) (в работе)
19. «Simulation, Part II» (May 9, 1995) готово
20. «Simulation, Part III» (May 11, 1995)
21. «Fiber Optics» (May 12, 1995) в работе
22. «Computer Aided Instruction» (May 16, 1995) (в работе)
23. «Mathematics» (May 18, 1995) Глава 23. Математика
24. «Quantum Mechanics» (May 19, 1995) Глава 24. Квантовая механика
25. «Creativity» (May 23, 1995). Перевод: Глава 25. Креативность
26. «Experts» (May 25, 1995) Глава 26. Эксперты
27. «Unreliable Data» (May 26, 1995) (в работе)
28. «Systems Engineering» (May 30, 1995) Глава 28. Системная Инженерия
29. «You Get What You Measure» (June 1, 1995) Глава 29. Вы получаете то, что вы измеряете
30. «How Do We Know What We Know» (June 2, 1995) в работе
31. Hamming, «You and Your Research» (June 6, 1995). Перевод: Вы и ваша работа

Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru

Let's block ads! (Why?)