— Мой доклад будет про онлайн-оценку качества для эффективной разработки веб-сервисов. Сначала расскажу о нашей команде, о том, чем мы занимаемся.

Мы в отделе научных исследований занимаемся самыми разными областями компьютерных наук. Это и анализ данных, и теоретические основы машинного обучения, обработка естественных текстов, компьютерное зрение и информационный поиск, а также иногда удается позаниматься аукционами и теорией игр.

Наш небольшой отдел постоянно публикуется на ведущих конференциях в этих областях, таких как NIPS, ICML, KDD, CVPR, ACL и т. д.
Здесь лишь те статьи, которые были опубликованы за последние несколько лет.


В сегодняшнем докладе расскажу об одном из направлений, которым мы очень концентрировано занимались в последние годы. Это онлайн-оценка качества веб-сервисов.
За последние пять лет мне и моим коллегам удалось внести существенный вклад в развитие этой тематики, мы опубликовали 14 статей на ведущих конференциях. Одна из них получила награду лучшей статьи на ведущей конференции по информационному поиску в 2015 году.
Онлайн-оценка качества в процессе разработки веб-сервисов или продукта играет ключевую роль для принятия решения о том, стоит ли запускать новую функциональность. Давайте посмотрим, как этот процесс устроен в Яндексе.

В каждый момент проводятся десятки экспериментов. Пример эксперимента приведен на этом слайде. Мы видим два варианта выдачи по одному и тому же поисковому запросу. Рядом с результатами правой выдачи присутствуют миниатюрные картинки.
Как вы считаете, правый вариант выдачи лучше, чем левый, и улучшает сервис? Правильный ответ скажу позже.

На слайде опять приведены два варианта выдачи на один и тот же поисковый запрос. На правом варианте отсутствует фактоид.
Как вы считаете, правый вариант сервиса лучше, чем левый? Правильный ответ скажу позже.
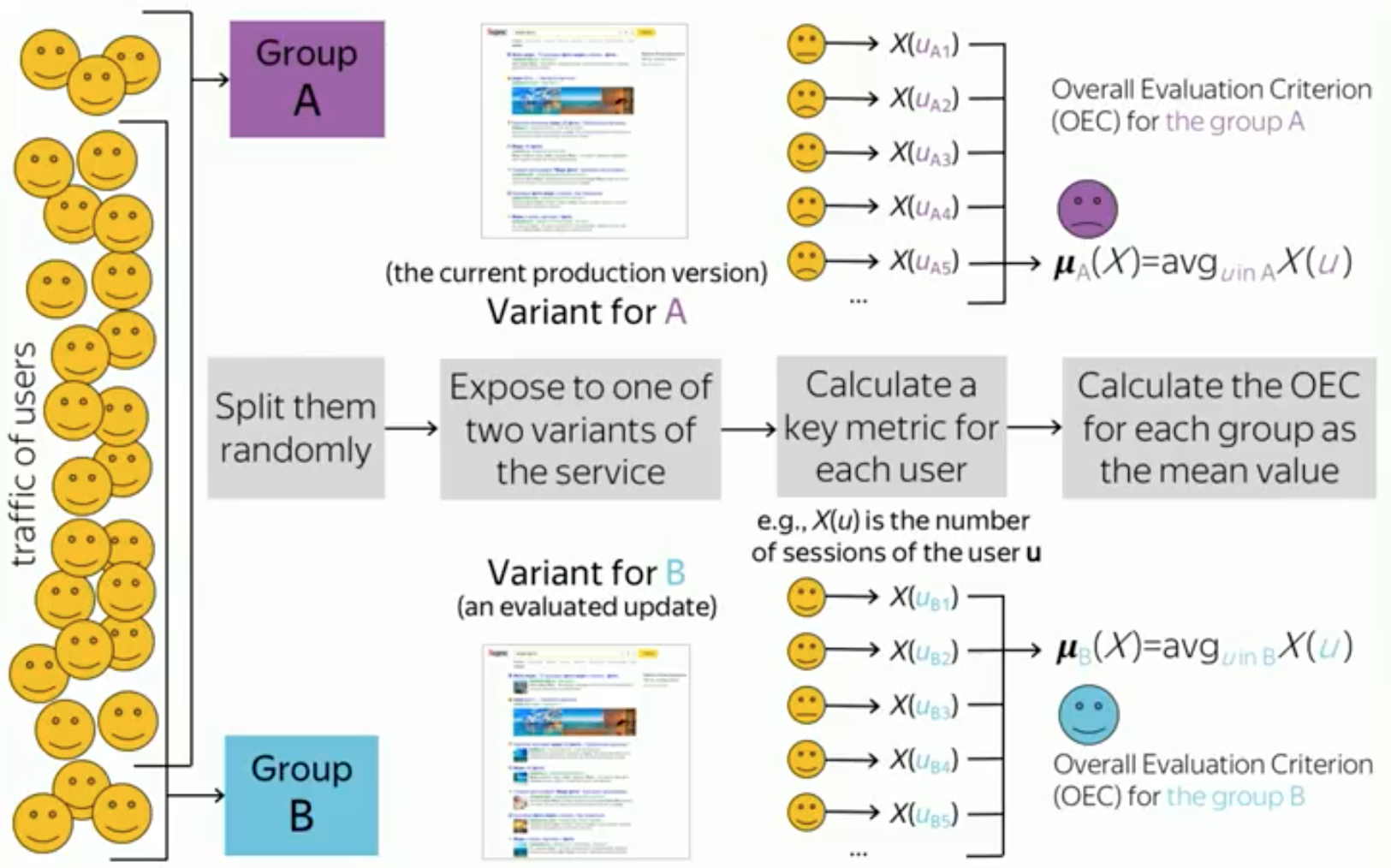
Ответ на мои запросы сильно зависит от того, что мы вкладываем в понятие «улучшить». Поэтому давайте разберемся, что же находится под капотом AB-тестирования.
Нелишне вспомнить ключевые опорные моменты этого процесса. Для каждого эксперимента выделяется некоторый набор пользователей, который будет участвовать в этом эксперименте. Далее этот набор делится случайным образом на две группы. Например, поровну. Мы половину пользователей определяем в группу А, а половину — в группу В.
Затем каждой из этих групп показывается собственная версия вашего сайта, веб-сервиса или продукта. Например, группе А вы показываете текущую рабочую версию продукта, которая показывается большинству пользователей, а группе В — новую экспериментальную версию продукта, где зашита, например, новая функциональность, которую вы хотите протестировать.
После истечения какого-то времени, вы завершаете эксперимент, например, через неделю или две, и собираете со всех пользователей некоторую статистику, информацию об их поведении. Например, это может быть одно число для каждого пользователя. Это число — например, количество сессий пользователей на сайте в течение эксперимента — мы называем ключевой метрикой. Мы эти числа агрегируем среди всех пользователей в каждой группе, и получаем число для каждой из групп. Иногда это называется агрегированной метрикой или критерием оценки. Таким образом мы получаем по одному числу для каждой группы. Для нашего примера это среднее количество сессий на пользователя в каждой из групп.
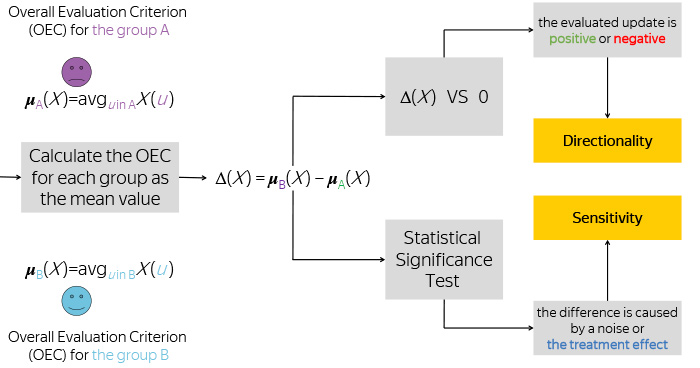
Имея эти два числа, мы берем их разницу, и сравниваем эту разницу с нулем, чтобы понять, изменилась ли ваша метрика в положительную сторону или в отрицательную, а также запоминаем, насколько большая эта разница была.
Но этого вам недостаточно знать. Все мы знаем, что разделение пользователей на группы случайно, поведение пользователей тоже вполне подчиняется случайному процессу, а потому наблюдение вашей разницы — это некая случайная величина. Или реализация случайной величины.
Чтобы понять, отличается ли та наблюдаемая разница от возможного шума в данных, мы применяем статистический тест. Например, это может быть всем известный Т-тест Стьюдента.
После этого мы принимаем решение, действительно ли то изменение, которое мы наблюдаем, является следствием новой функциональности, которую мы тестируем. Или же это наблюдение — всего лишь шум в данных, а в действительности ваша новая функциональность никакого влияния на пользователей не оказала, по крайней мере, с точки зрения этой метрики.
Эти два процесса подводят нас к двум ключевым свойствам или определениям метрики, которыми должна метрика обладать. Давайте подробнее разберемся в этих двух свойствах.
В действительности наблюдаемая разница средних величин метрики Х для версий А и В является несмещенной оценкой среднего эффекта влияния, который в свою очередь также является разницей, но уже математических ожиданий метрики Х для версии А и версии В.
Таким образом нужно всегда помнить, что наблюдаемая дельта является реализацией случайной величины. Давайте представим, что в результате эксперимента мы получили дельту, равную одному проценту увеличения числа сессий на пользователя. Много это или мало? На экране это указано как большой отрезок. Наверное, это очень большая величина.

Но чтобы в этом разобраться, надо выяснить, можем ли мы наблюдать такую дельту, если версии сервиса неразличимы. Средний эффект влияния равен нулю.
Часто это условие еще называют нулевой гипотезой. Здесь все сильно зависит от того, какого распределение этой дельны. На экране приведены два возможных варианта распределений. И нетрудно заметить, что в случае, если мы имеем дело с распределением синего цвета, то вероятность наблюдать эту дельту намного меньше при нулевой гипотезе, чем если мы имеем дело с распределением зеленого цвета.
Чтобы понимать или быть уверенным в значимости того наблюдения или наблюдаемого изменения, мы вычисляем вероятность наблюдать эту дельту или больше при условии нулевой гипотезы.
Чтобы вычислить эту вероятность, как правило, мы применяем всем известный Т-тест Стьюдента, который основан на Т-статистике.

Вот ее формула, в числителе дельта, а в знаменателе еще две величины. Первая величина — дисперсия метрики Х для каждой из групп. Вторая — размер выборки каждой из групп. Чем выше модуль Т-статистики, тем более мы уверены в наблюдаемом изменении в нашей дельте.

Давайте внимательнее разберемся, при каких условиях модуль Т-статистики будет больше. Рассмотрим выражение для Т-статистики. Оно зависит от трех величин. Понятно, что этот модуль Т-статистики будет выше, если числитель будет больше, если эксперимент будет сильно менять метрику. Только при этом условии числитель будет больше. Например, если эксперимент будет сдвигать метрику на 10%, на 20%, на 30%. Какие еще большие числа мы можем вообразить?
Но такое бывает очень редко, когда ваш сервис много лет развивается и улучшается. Кроме того, размер изменения в эксперименте зависит от самого эксперимента, от функциональности, которую вы тестируете. Если вы тестируете функциональность, которая очень слабо влияет на пользователей, то и дельта будет очень маленькой. Поэтому числитель нам не подвластен. И поэтому если мы хотим повышать Т-статистику, то от нас зависит только знаменатель, только его мы можем менять.
Самый простой способ — повысить количество пользователей, которое мы используем в эксперименте. Но этот способ плохой, потому что снижает пропускную способность экспериментальной платформы, а значит, ее эффективность.
Альтернативный способ — снижать дисперсию метрики. Таким образом мы постепенно приходим к такому понятию как чувствительность метрики. Для простоты будем считать, что это средний модуль Т-статистики по всем экспериментам. Чем выше чувствительность, тем более слабые изменения мы можем замечать в нашем эксперименте. Или альтернативно мы можем использовать меньше пользователей в эксперименте, чтобы наблюдать те же изменения, которые наблюдали и раньше, но на том же уровне значимости, что и при исходном количестве пользователей.

Основным ключом к повышению чувствительности является уменьшение дисперсии метрики, о чем я говорил раньше.

Перейдем ко второму понятию — метрике направленности.
Рассмотрим две метрики: количество кликов на пользователя за время эксперимента и количество сессий на пользователя. Оказывается, в данном примере количество кликов на пользователя увеличилось, что говорит о положительном эффекте. Посетители лучше используют результаты выдачи.
Кроме того, количество сессий на пользователя также выросло. Это означает, что пользователи стали чаще возвращаться на наш сайт, чтобы решать повседневные задачи.

Во втором примере мы также наблюдаем увеличение количества кликов, поскольку в правом варианте результатов отсутствует фактоид на тот запрос, который пользователь задал. Следовательно этот ответ они должны искать, переходя на сайт, и совершать больше кликов. Несмотря на это, правый вариант сервиса без фактоида приводит к снижению числа сессий на пользователя. И на этом примере мы видим, что кликовая метрика активности пользователей вступает в противоречие с более долгосрочной метрикой, измеряющей лояльность пользователей, а потому более подходящей для срочной цели.
В итоге что мы имеем? Количество кликов увеличено, а количество сессий уменьшено в эксперименте.
Если коротко подводить итог, то хорошей метрикой мы называем ту, которая имеет ясную интерпретацию направлений ее изменения или направленности. И это является ключевым критерием при выборе метрики. Без этого свойства любому аналитику очень трудно сделать правильный вывод, принять правильное решение об успешности или неуспешности тестируемого обновления или функциональности.

Рассмотрим некоторый класс метрик пользовательской увлеченности для примера. Как правило, к этому классу метрик относят две группы метрик. Первая группа — метрики лояльности, как количество сессий на пользователя, время его отсутствия и т. д. Вторая группа состоит из метрик активности. Это такие метрики как количество кликов пользователя, количество запросов пользователя, время, проведенное на сайте, и т. д.
Первая категория метрик обладает очень хорошей направленностью. Интерпретация ее изменений очень прозрачна, и как правило, коррелирует с долгосрочными целями компании, на долгое существование и развитие.

При этом эти метрики имеют очень низкую чувствительность. В наших экспериментах такие метрики очень тяжело сдвинуть, очень тяжело изобрести новую функциональность, которая существенно повысит лояльность пользователей или количество задач, которые они решают в своей повседневной жизни через наш сервис.

Напротив, метрики активности имеют путанную направленность, но при этом имеют очень высокую чувствительность. Их очень легко сдвинуть. Любой эксперимент, который внедряет функциональность, изменяющую или затрагивающую дизайн, сразу приводит к изменению метрики: если пользователям не нравится эта новая функциональность, они вынуждены ее изучить. Попробовать, посмотреть, что с ней происходит. В результате они совершают больше или меньше кликов, если отвлекаются на совершение другого действия, и важной задачей является увеличение чувствительности метрик лояльностей, но при сохранении их направленности.
Суммируя, мы имеем следующую задачу: улучшить чувствительность ключевой метрики, но сохранить ее направленность. Чувствительность, потому что это позволит выявить более слабые изменения метрики, а также использовать меньше пользователей. И то, и другое повышает эффективность или производительность платформы по проведению экспериментов. А направленность нужно сохранить, чтобы делать правильные выводы об изменении качества системы.
Далее я расскажу об одном из приемов повышения чувствительности метрики, который применяется в Яндексе, и про который мы опубликовали статью на конференции KDD в 2016 году.
Данная техника основана на вычитании предсказаний значения метрики из самой метрики для понижения ее дисперсии.

Давайте рассмотрим временной отрезок, который схематично разбит на два подинтервала, на период времени, в котором проводится эксперимент, и на некоторый период времени до этого эксперимента. Предположим, мы рассматриваем в качестве ключевой метрики количество сессий, проведенных данным пользователем на нашем сайте в течение эксперимента.
Пусть также у нас имеется некоторый набор показателей, фичей, характеризующих пользователя. Например, количество сессий этого пользователя, которые он провел в предэкспериментальный период. Аналогично в качестве фичей могут выступать другие метрики, которые мы измерили в этом периоде. Кроме того мы можем использовать какие-то статистические характеристики пользователя, например, пол, возраст, какие-то еще данные, если они нам доступны.
Наконец, пусть мы имеем некоторый предсказатель, который на основе данных показателей предсказывает нашу ключевую метрику. Например, это может быть простая линейная модель. Например, самым простым и хорошим предсказателем является количество сессий, проведенных пользователем в предэкспериментельный период, если длительность предэкспериментального периода равна длительности эксперимента.

Суть этой техники составляет следующий подход: мы вместо того, чтобы использовать метрику Х, используем метрику Y, которая равна метрике Х, минус предсказанное значение метрики Х. На нашем примере это означает, что вместо того, чтобы смотреть на количество сессий в эксперименте, мы будем смотреть, каково изменение в количестве сессий по сравнению с тем, сколько мы ожидали на основе нашего предсказания.

Давайте разберемся, почему эта техника работает. На самом деле, мы можем доказать следующие теоретические гарантии про нашу технику. Во-первых, если ваш предсказатель не зависит от экспериментальной выдачи, которую вы проверяете или тестируете. Например, вследствие того, что вы не используете факторы, собранные с пользователя, после начала эксперимента. В этом случае вы гарантировано получаете следующее утверждение: средний эффект влияния новой метрики равен в точности среднему эффекту влияния старой метрики. А значит, наблюдаемое изменение метрики Y будет несмещенной оценкой исходной метрики Х. Таким образом мы гарантируем, что метрика Y имеет ту же направленность, что и метрика Х.

Давайте рассмотрим теперь вопрос чувствительности. Предположим, что вы используете предсказатель, который является оптимальным среди моделей машинного обучения, которые замкнуты относительно умножения на скалярную величину. Тогда нетрудно доказать, что дисперсия метрики Y будет гарантировано меньше дисперсии метрики Х. Это означает, что метрика Y точно понижает дисперсию, либо, как мы выяснили, повышает чувствительность.
Таким образом мы почти достигли необходимой цели, поскольку мы получили новую метрику, которая сохраняет направленность и вообще потенциально может повысить чувствительность. Или понизить дисперсию.
Давайте поймем, насколько мы можем понизить.
Если мы дополнительно потребуем, чтобы ваш предсказатель был оптимален среди класса моделей, которые замкнуты относительно прибавления скалярной величины, тогда дисперсия метрики Y будет в точности равна среднеквадратичному отклонению вашего предсказателя. Это очень сильный и важный результат. Таким образом степень, насколько вы понижаете дисперсию, равна в точности степени того, насколько вы улучшаете ваш предсказатель. Чем лучше вы делаете ваш предсказатель, либо за счет модели, либо за счет факторов, тем сильнее вы понижаете дисперсию метрик и тем выше растет ее чувствительность.

Подведем итог. Новая метрика получилась сонаправленной с метрикой Х. Новая метрика Y понижает дисперсию или повышает чувствительность метрики Х. И кроме того, вы можете контролировать степень повышения чувствительности за счет улучшения качества предсказания вашей исходной метрики Х.

Какие предположения мы для этого использовали? Во-первых, независимость предсказателя от эксперимента, а во-вторых, тот факт, что ваш предсказатель является оптимальным с точки зрения среднеквадратичного отклонения в классе моделей, замкнутых относительно умножения и прибавления константы.
На самом деле, таким свойством обладают линейные модели, а также широко используемые деревья решений, которые построены градиентным бустингом.

Мы провели эксперименты, вернее исследования, в которых рассмотрели количество сессий в качестве ключевой метрики, использовали 51 фактор о пользователе, в частности количество сессий в предэкспериментальный период, и время первого захода пользователя в эксперимент. Кроме того, мы использовали 161 AB-тест как выборку, на которой вычисляли показатели производительности нашего подхода.
В результате нам удалось достигнуть следующих результатов. Мы понизили дисперсию исходной метрики лояльности на 63%, что эквивалентно трехкратному сокращению числа пользователей, которые нам необходимы в эксперименте, чтобы получать Т-статистики того же уровня, как с исходной метрикой.
Наконец, мы в два раза большем количестве экспериментов замечали статистически значимые изменения. Все подробности об этом исследовании и эксперименте вы можете с легкостью прочитать в нашей статье, которую мы опубликовали в 2016 году.

Давайте еще раз подведем, в качестве напоминания, основные моменты этой техники. Первое — вместо того, чтобы использовать в качестве ключевой метрики ту метрику, на которую вы смотрите, берите и вычитайте из нее предсказанные значения этой самой метрики. Кроме того, используйте продвинутые методы машинного обучения, чтобы качество предсказания вашего предсказателя было наилучшим. За счет этого вы сможете добиться максимального сокращения дисперсии и повышения ее чувствительности.
Наконец, обязательно следите за тем, чтобы факторы, которые используются в вашем предсказателе, были независимы от измеряемого или тестируемого функционала. Это будет гарантировать, что новая метрика не будет путать вас в принятии решений, то есть будете иметь ту же направленность, что и метрика Х.

Если вы хотите знать больше, во-первых, наша команда Яндекса организует полнодневный туториал на ведущей международной конференции по интернет-технологиям, ранее называемой WWW, сейчас это The Web Conference. Если вы случайно окажетесь во Франции в конце апреля, то можете заглянуть и узнать в деталях, как устроена в Яндексе платформа для экспериментов, с какими подводными камнями можно столкнуться при ее развитии, а также какие современные технологии в ней применяют (на момент публикации расшифровки конференция уже прошла, слайды с указанного туториала можно найти по QR-коду — прим. ред.).

Поскольку не все в зале имеют возможность побывать на нашем туториале, мы готовим онлайн-курс для Coursera, который выйдет ориентировочно этим летом. И мы ожидаем, что осветим там широко также тему онлайн-оценки качества. Спасибо за внимание.
Комментариев нет:
Отправить комментарий