Эксперт в области data science и руководитель компании STATWORX Себастьян Хайнц опубликовал на Medium руководство по созданию модели глубокого обучения для прогнозирования цен акций на бирже с использованием фреймворка TensorFlow. Мы подготовили адаптированную версию этого полезного материала.
Автор разместил итоговый Python-скрипт и сжатый датасет в своем репозитории на GitHub.
Импорт и подготовка данных
Хайнц экспортировал биржевые данных в csv-файл. Его датасет содержал n = 41266 минут данных, охватывающих торги 500 акциями в период с апреля по август 2017, также в него вошла информация по цене индекса S&P 500.
# Импорт данных
data = pd.read_csv('data_stocks.csv')
# Сброс переменной date
data = data.drop(['DATE'], 1)
# Размерность датасета
n = data.shape[0]
p = data.shape[1]
# Формирование данных в numpy-массив
data = data.values
Так выглядит временной ряд индекса S&P, построенный с помощью pyplot.plot(data['SP500']):

Интересный момент: поскольку конечная цель заключается в «предсказании» значение индекса в ближайшем будущем, его значение сдвигается на одну минуту вперед.
Подготовка данных для тестирования и обучения
Набор данных был разбит на два — одна часть для тестирования, а вторая для обучения. При этом, данные для обучения составили 80% от всего их объема и охватили период с апреля до приблизительно конца июля 2017 года, данные для тестирования оканчивались августом 2017 года.
# Данные для тестирования и обучения
train_start = 0
train_end = int(np.floor(0.8*n))
test_start = train_end
test_end = n
data_train = data[np.arange(train_start, train_end), :]
data_test = data[np.arange(test_start, test_end), :]
Существует множество подходов к кросс-валидации временных рядов, от генерации прогнозов с или без перенастройкой модели (refitting) до более сложных концептов вроде bootstrap-ресемплирования временных рядов. В последнем случае данные разбиваются на повторяющиеся выборки начиная с начала сезонной декомпозиции временного ряда — это позволяет симулировать выборки, которые следуют тому же сезонному паттерну, что и оригинальный временной ряд, но не полностью копируют его значения.
Масштабирование данных
Большинство архитектур нейронных сетей используют масштабирование входных данных (а иногда и выходных). Причина в том, что большинство функций активации нейронов вроде сигмовидной или гиперболической касательной (tanx) определены на интервалах [-1, 1] или [0, 1], соответственно. В настоящее время, наиболее часто используются активации выпрямленной линейной единицей (ReLU). Хайнц решил масштабировать входные данные и цели, использовав для этой цели MinMaxScaler в Python:
# Масштабирование данных
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(data_train)
data_train = scaler.transform(data_train)
data_test = scaler.transform(data_test)
# Построение X и y
X_train = data_train[:, 1:]
y_train = data_train[:, 0]
X_test = data_test[:, 1:]
y_test = data_test[:, 0]
Примечание: следует быть внимательным при выборе части данных и времени для масштабирования. Распространенная ошибка здесь — масштабировать весь датасет до его разбиения на тестовые и обучающие данные. Это ошибка, поскольку масштабирование запускает подсчет статистики, то есть минимумов/максимумов переменных. При осуществлении прогнозирования временных рядов в реальной жизни, на момент их генерации у вас не может быть информации из будущих наблюдений. Поэтому подсчет статистики должен производиться на тренировочных данных, а затем полученный результат применяться к тестовым данным. Таким образом, вы сможете получить информацию «из будущего», что хорошо влияет на метрики прогнозирования.
Введение в TensorFlow
TensorFlow — отличный продукт, в настоящий момент это самый популярный фреймворк для решения задач машинного обучения и создания нейронных сетей. Бэкенд продукта основан основан на C++, однако для управления обычно используется Python (также существует замечательная библиотека TensorFlow для R). TensorFlow использует концепцию графического представления вычислительных задач. Такой подход позволяет пользователям определять математические операции в качестве элементов графов данных, переменных и операторов. Поскольку нейронные сети, по сути, и являются графами данных и математических операций, TensorFlow отлично подходит для работы с ними и машинного обучения. В примере ниже представлен граф, который решает задачу сложения двух чисел:
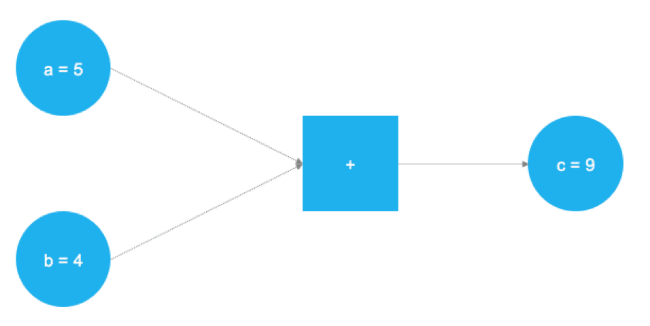
На рисунке выше представлены два числа, которые нужно сложить. Они хранятся в переменных a и b. Значения путешествуют по графу и попадают в узел, представленный квадратом, где и происходит сложение. Результат операции записывается в другую переменную c. Использованные переменные можно рассматривать как плейсхолдеры. Любые числа, попадающие в a и b, складываются, а результат записывается в c.
Именно так и работает TensorFlow — пользователь определяет абстрактное представление модели (нейронной сети) через плейсхолдеры и переменные. После этого первые наполняются реальными данными и происходят вычисления. Тестовый пример выше описывается следующим кодом в TensorFlow:
# Импорт TensorFlow
import tensorflow as tf
# Определение a и b в качестве плейсхолдеров
a = tf.placeholder(dtype=tf.int8)
b = tf.placeholder(dtype=tf.int8)
# Определение сложения
c = tf.add(a, b)
# Инициализация графа
graph = tf.Session()
# Запуск графа
graph.run(c, feed_dict={a: 5, b: 4})
После импорта библиотеки TensorFlow с помощью tf.placeholder() определяются два плейсхолдера. Они соответствуют двум голубым кругам в левой части изображения выше. После этого, с помощью tf.add() определяется операция сложения. Результат операции — это c = 9. При настроенных плейсхолдерах граф может быть исполнен при любых целочисленных значениях a и b. Понятно, что этот пример крайне прост, а нейронные сети в реальной жизни куда сложнее, но он позволяет понять принципы работы фреймворка.
Плейсхолдеры
Как сказано выше, все начинается с плейсхолдеров. Для того, чтобы реализовать модель, нужно два таких элемента: X содержит входные данные для сети (цены акций всех элементов S&P 500 в момент времени T = t) и выходные данные Y (значение индекса S&P 500 в момент времени T = t + 1).
Форма плейсхолдеров соответствует [None, n_stocks], где [None] означает, что входные данные представлены в виде двумерной матрицы, а выходные данные — одномерного вектора. Важно понимать, какая форма входных и выходных данных нужна нейросети и соответственным образом их организовать.
# Плейсхолдер
X = tf.placeholder(dtype=tf.float32, shape=[None, n_stocks])
Y = tf.placeholder(dtype=tf.float32, shape=[None])
Аргумент None означает, что в этой точке мы еще не знаем число наблюдений, которые пройдут через граф нейросети во время каждого запуска, поэтому он остается гибким. Позднее будет определена переменная batch_size, которая контролирует количество наблюдений в ходе обучающего «прогона».
Переменные
Помимо плейсхолдеров, во вселенной TensorFlow есть и другой важнейший элемент — это переменные. Если плейсхолдеры используются для хранения входных и целевых данных в графе, то переменные служат гибкими контейнерами внутри графа. Им позволено изменяться в процессе выполнения графа. Веса и смещения представлены переменными для того, чтобы облегчить адаптацию во время обучения. Переменные необходимо инициализировать перед началом обучения.
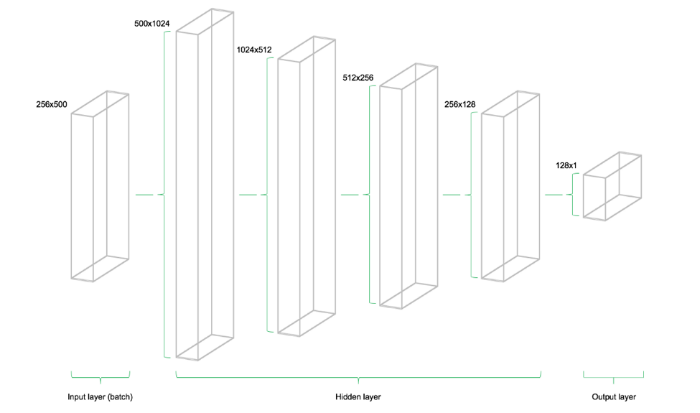
Модель состоит из четырех скрытых уровней. Первый содержит 1024 нейрона, что чуть более чем в два раза превышает объем входных данных. Последующие скрытые уровни всегда в два раза меньше предыдущего — они объединяют 512, 256 и 128 нейронов. Снижение числа нейронов на каждом уровне сжимает информацию, которую сеть обработала на предыдущих уровнях. Существуют и другие архитектуры и конфигурации нейронов, но в этом руководстве используется именно такая модель:
# Параметры архитектуры модели
n_stocks = 500
n_neurons_1 = 1024
n_neurons_2 = 512
n_neurons_3 = 256
n_neurons_4 = 128
n_target = 1
# Уровень 1: Переменные для скрытых весов и смещений
W_hidden_1 = tf.Variable(weight_initializer([n_stocks, n_neurons_1]))
bias_hidden_1 = tf.Variable(bias_initializer([n_neurons_1]))
# Уровень 2: Переменные для скрытых весов и смещений
W_hidden_2 = tf.Variable(weight_initializer([n_neurons_1, n_neurons_2]))
bias_hidden_2 = tf.Variable(bias_initializer([n_neurons_2]))
# Уровень 3: Переменные для скрытых весов и смещений
W_hidden_3 = tf.Variable(weight_initializer([n_neurons_2, n_neurons_3]))
bias_hidden_3 = tf.Variable(bias_initializer([n_neurons_3]))
# Уровень 4: Переменные для скрытых весов и смещений
W_hidden_4 = tf.Variable(weight_initializer([n_neurons_3, n_neurons_4]))
bias_hidden_4 = tf.Variable(bias_initializer([n_neurons_4]))
# Уровень выходных данных: Переменные для скрытых весов и смещений
W_out = tf.Variable(weight_initializer([n_neurons_4, n_target]))
bias_out = tf.Variable(bias_initializer([n_target]))
Важно понимать, какие размеры переменных требуются для разных уровней. Практическое правило мультиуровневых перцептронов гласит, что размер предыдущего уровня — это первый размер текущего уровня для матриц весов. Звучит сложно, но суть в том, что каждый уровень передает свой вывод в качестве ввода следующему уровню. Размеры смещений равняются второму размеру матрицы весов текущего уровня, что соответствует число нейронов в уровне.
Разработка архитектуры сети
После определения требуемых весов и смещений переменных, сетевой топологии, необходимо определить архитектуру сети. Таким образом, плейсхолдеры (данные) и переменные (веса и смещения) нужно объединить в систему последовательных матричных умножений. Скрытые уровни сети трансформируются функциями активации. Эти функции — важные элементы сетевой инфраструктуры, поскольку они привносят в систему нелинейность. Существуют десятки функций активации, и одна из самых распространенных — выпрямленная линейная единица (rectified linear unit, ReLU). В данном руководстве используется именно она:
# Скрытый уровень
hidden_1 = tf.nn.relu(tf.add(tf.matmul(X, W_hidden_1), bias_hidden_1))
hidden_2 = tf.nn.relu(tf.add(tf.matmul(hidden_1, W_hidden_2), bias_hidden_2))
hidden_3 = tf.nn.relu(tf.add(tf.matmul(hidden_2, W_hidden_3), bias_hidden_3))
hidden_4 = tf.nn.relu(tf.add(tf.matmul(hidden_3, W_hidden_4), bias_hidden_4))
# Выходной уровень (должен быть транспонирован)
out = tf.transpose(tf.add(tf.matmul(hidden_4, W_out), bias_out))
Представленное ниже изображение иллюстрирует архитектуру сети. Модель состоит из трех главных блоков. Уровень входных данных, скрытые уровни и выходной уровень. Такая инфраструктура называется упреждающей сетью (feedforward network). Это означает что куски данных продвигаются по структуре строго слева-направо. При других реализациях, например, в случае рекуррентных нейронных сетей, данные могут перетекать внутри сети в разные стороны.
Функция стоимости
Функция стоимости сети используется для генерации оценки отклонения между прогнозами сети и реальными результатами наблюдений в ходе обучения. Для решения проблем с регрессией используют функцию средней квадратичной ошибки (mean squared error, MSE). Данная функция вычисляет среднее квадратичное отклонение между предсказаниями и целями, но вообще для подсчета отклонения между может быть использована любая дифференцируемая функция.
# Функция стоимости
mse = tf.reduce_mean(tf.squared_difference(out, Y))
При этом, MSE отображает конкретные сущности, которые полезны для решения общей проблемы оптимизации.
Оптимизатор
Оптимизатор берет на себя необходимые вычисления, требующиеся для адаптации весов и переменных отклонений нейросети в ходе обучения. Эти вычисления ведут к подсчетам так называемых градиентов, которые обозначают направление необходимого изменения отклонений и весов для минимизации функции стоимости. Разработка стабильного и быстрого оптимизатора — одна из основных задач создателей нейронных сетей.
# Оптимизатор
opt = tf.train.AdamOptimizer().minimize(mse)
В данном случае используется один из наиболее распространенных оптимизаторов в сфере машинного обучения Adam Optimizer. Adam — это аббревиатура для фразы “Adaptive Moment Estimation” (адаптивная оценка моментов), он представляет собой нечто среднее между двумя другими популярными оптимизаторами AdaGrad и RMSProp
Инициализаторы
Инициализаторы используются для инициализации переменных перед стартом обучения. Поскольку нейронные сети обучаются с помощью численных техник оптимизации, начальная точки проблемы оптимизации — это один из важнейших факторов на пути поиска хорошего решения. В TensorFlow существуют различные инициализаторы, каждый из которых использует собственный подход. В данном руководстве использован tf.variance_scaling_initializer(), который реализует одну из стандартных стратегий инициализации.
# Инициализаторы
sigma = 1
weight_initializer = tf.variance_scaling_initializer(mode="fan_avg", distribution="uniform", scale=sigma)
bias_initializer = tf.zeros_initializer()
Примечание: в TensorFlow можно определять несколько функций инициализации для различных переменных внутри графа. Однако в большинстве случаев достаточно унифицированной инициализации.
Настройка нейросети
После определения плейсхолдеров, переменных, инициализаторов, функций стоимости и оптимизаторов, модель необходимо обучить. Обычно для этого используется подход мини-партий (minibatch training). В ходе такого обучения из набора данных для обучения отбираются случайные семплы данных размера n = batch_size и загружаются в нейросеть. Набор данных для обучения делится на n / batch_size кусков, которые затем последовательно отправляются в сеть. В этот момент в игру вступают плейсхолдеры X и Y. Они хранят входные и целевые данные и отправляют их в нейросеть.
Семплированные данные X проходят по сети до достижения выходного уровня. Затем TensorFlow сравнивает сгенерированные моделью прогнозы с реально наблюдаемыми целями Y в текущем «прогоне». После этого TensorFlow выполняет этап оптимизации и обновляет параметры сети, после обновления весов и отклонений, процесс повторяется снова для нового куска данных. Процедура повторяется до того момента, пока все «нарезанные» куски данных не будут отправлены в нейросеть. Полный цикл такой обработки называется «эпохой».
Обучение сети останавливается по достижению максимального числа эпох или при срабатывании другого определенного заранее критерия остановки.
# Создание сессии
net = tf.Session()
# Запуск инициализатора
net.run(tf.global_variables_initializer())
# Настройка интерактивного графика
plt.ion()
fig = plt.figure()
ax1 = fig.add_subplot(111)
line1, = ax1.plot(y_test)
line2, = ax1.plot(y_test*0.5)
plt.show()
# Количество эпох и размер куска данных
epochs = 10
batch_size = 256
for e in range(epochs):
# Перемешивание данных для обучения
shuffle_indices = np.random.permutation(np.arange(len(y_train)))
X_train = X_train[shuffle_indices]
y_train = y_train[shuffle_indices]
# Обучение мини-партией
for i in range(0, len(y_train) // batch_size):
start = i * batch_size
batch_x = X_train[start:start + batch_size]
batch_y = y_train[start:start + batch_size]
# Run optimizer with batch
net.run(opt, feed_dict={X: batch_x, Y: batch_y})
# Показать прогресс
if np.mod(i, 5) == 0:
# Prediction
pred = net.run(out, feed_dict={X: X_test})
line2.set_ydata(pred)
plt.title('Epoch ' + str(e) + ', Batch ' + str(i))
file_name = 'img/epoch_' + str(e) + '_batch_' + str(i) + '.jpg'
plt.savefig(file_name)
plt.pause(0.01)
# Вывести финальную фукнцию MSE после обучения
mse_final = net.run(mse, feed_dict={X: X_test, Y: y_test})
print(mse_final)
В ходе обучения оценивались предсказания, сгенерированные сетью на тестовом наборе, затем осуществлялась визуализация. Кроме того, изображения выгружались на диск и позднее из них создавалась видео-анимация процесса обучения:
Как видно, нейросеть быстро адаптируется к базовой форме временного ряда и продолжает искать наилучшие паттерны данных. После прошествия 10 эпох мы получаем результаты, очень близкие к тестовым данным. Финальное значение функции MSE составляет 0,00078 (очень маленькое значение из-за того, что цели масштабированы). Средняя абсолютная процентная погрешность прогноза на тестовом наборе равняется 5,31% — очень хороший результат. Важно понимать, что это лишь совпадение с тестовыми, а не реальными данными.
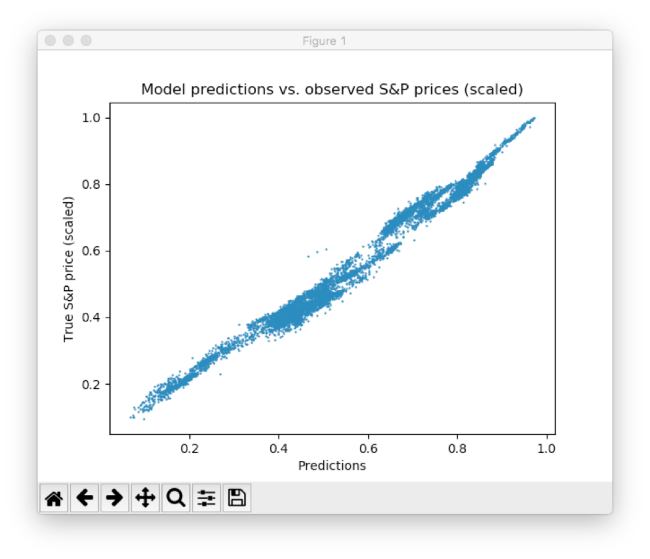
График рассеяния между предсказанными и реальными ценами S&P
Этот результат можно еще улучшить множеством способов от проработки уровней и нейронов, до выбора иных схем инициализации и активации. Кроме того, могут быть использованы различные типы моделей глубокого обучения, вроде рекуррентных нейросетей — это также может приводить к лучшим результатам.
Комментариев нет:
Отправить комментарий