Введение
Для определения баллистико-временных характеристик движения центра масс парашютиста приходится выбирать упрощенную математическую модель, вполне доступную для аналитического исследования и в то же время сохраняющую наиболее характерные черты исходного объекта.
Для построения упрощённых математических моделей движения парашютиста проводится анализ, определение, систематизация постоянных и временных параметров.
Регулярных и достаточно обоснованных методов построения нелинейных математических моделей в настоящее время не существует, однако для решения частных задач, при правильном составлении исходных систем нелинейных дифференциальных уравнений, численные методы их решения могут давать вполне адекватные результаты.
Целью настоящей публикации является составление и численное решение систем дифференциальных уравнений, описывающих все этапы движения парашютиста, десантируемого с самолёта с учётом влияния изменения с высотой и температурой массовой плотности воздуха.
Баллистико-временные характеристики движения парашютиста
К постоянным и ограничено изменяемым параметрам относятся:
Н – высота выброса парашютиста;
V0 – скорость самолета;
k – вес, рост парашютиста;
g – ускорение свободного падения;
ρ – плотность воздуха;
Т – температура воздуха.
К временным (переменным) параметрам относятся:
tn – время десантирования,
w – скорость ветра;
V – скорость парашютиста;
u – скорость восходящих (нисходящих) потоков;
d – снос (расстояние от проекции на землю точки выброса до точки приземления);
С – коэффициент лобового сопротивления десантируемого объекта;
F – мидель десантируемого объекта.
Этапы прыжка
Первый этап –свободное падение после отделения от самолета:

Второй этап – снижение на стабилизирующем парашюте:

Главное свойство стабилизирующего парашюта – стабилизация парашютиста в положении, наиболее удобном для работы основного парашюта.
Третий этап – наполнение купола основного парашюта:

Четвертый этап – снижение на раскрытом парашюте:

Составление системы дифференциальных уравнений для всех этапов прыжка с парашютом
Выберем неподвижную систему координат OXY с центром в точке выброса О. Ось ОX совпадает с направлением горизонтальной составляющей скорости самолета. Oсь OY направлена вертикально вверх в направлении, противоположном вертикальной скорости падения парашютиста.
Будем предполагать, что движение парашютиста плоское, и происходит в плоскости OXY. Эту модель прыжка можно рассматривать как модель прыжка в штилевую погоду без учёта влияния ветра.
Считаем, что на парашютиста, кроме веса, действует сила сопротивления воздуха, пропорциональная квадрату скорости парашютиста:
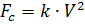 ,
,
где: 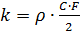 ,
, 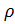 — плотность воздуха, С – коэффициент лобового сопротивления, F – мидель тела.
— плотность воздуха, С – коэффициент лобового сопротивления, F – мидель тела.
С увеличением высоты температура воздуха меняется:

Минимум температуры достигается уже на высоте в 10 км. и составляет -55 °С. Плотность воздуха зависит так же и от давления. Поэтому при расчётах баллистики парашютного прыжка удобно пользоваться следующей формулой для определения плотности воздуха [1]:
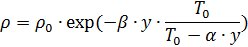 ,
,
где 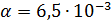 K/м;
K/м; 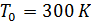 – температура на уровне моря; y – высота в м;
– температура на уровне моря; y – высота в м;  – плотность воздуха при y=0;
– плотность воздуха при y=0;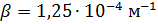 .
.
# -*- coding: utf8 -*-
from numpy import*
import matplotlib.pyplot as plt
beta=1.25*10**-4
alfa=6.5*10**-3
T0=300
y=arange(0,10000,1)
x=[exp(-beta*w*T0/(T0-alfa*w)) for w in y]
plt.title("Зависимость относительной \n плотности воздуха от высоты")
plt.plot(x,y)
plt.ylabel('Высота в м.')
plt.xlabel('Относительная плотность')
plt.grid(True)
plt.show()
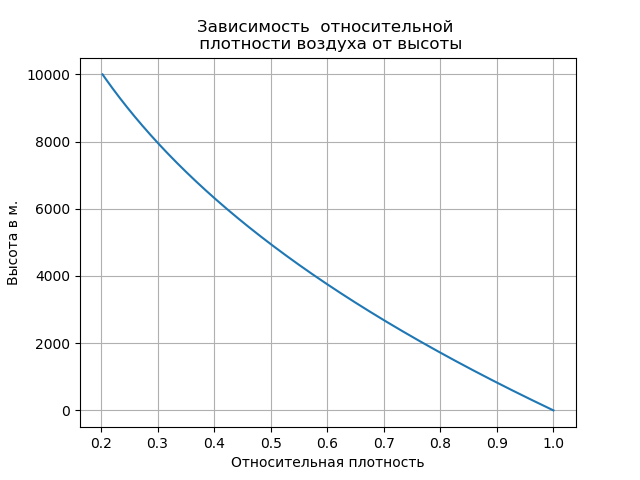
В практике расчетов за величину миделя принимают квадрат роста; значение С находят из таблицы [2]:

Через θ обозначен угол наклона траектории. При сделанных предположениях для компонент 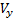 ,
, 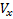 вектора скорости V имеем:
вектора скорости V имеем:

Поделив на m левые и правые части уравнений полученной системы и обозначив  через r, получим:
через r, получим:
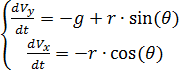 (1)
(1)
Запишем уравнения движения парашютиста в виде системы дифференциальных уравнений относительно функций V,θ,y(t),x(t).
Учитывая, что:
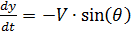 ,
,
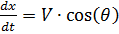 ,
,
и дифференцируя по времени соотношение:  , с учётом системы уравнений (1) получим:
, с учётом системы уравнений (1) получим:
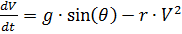 ,
,
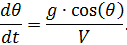 .
.
Таким образом, при начальных условиях:
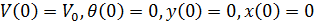 имеем следующую систему дифференциальных уравнений:
имеем следующую систему дифференциальных уравнений:
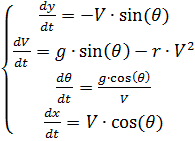
Численное решение системы дифференциальных уравнений (2) средствами Python
Для решения (2) перепишем её в следующем виде, введя управляемые по времени и плотности воздуха силы сопротивления стабилизирующего
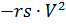
и основного
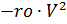
парашютов соответственно, умноженные на функции управления по времени ks(t) и ko(t):
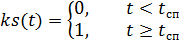
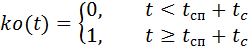 ,
,
где: 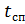 –время свободного падения парашютиста;
–время свободного падения парашютиста;  – время работы стабилизационного парашюта до открытия основного.
– время работы стабилизационного парашюта до открытия основного.
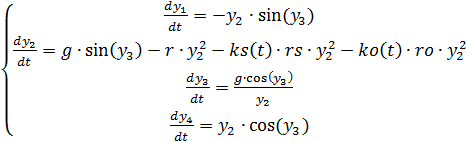 (3)
(3)
# -*- coding: utf8 -*-
from numpy import*
from scipy.integrate import odeint
import matplotlib.pyplot as plt
g=9.81#ускорение свободного падения м/с2
rou0=1.29#плотность воздуха кг/м3
Cp=0.3#коэффициент лобового сопротивления парашютиста
Cpar=0.75#коэффициент лобового сопротивления основного парашюта
mp=120#масса парашютиста с парашютом 100+20=120 кг.
s=0.8#мидель тела парашютиста м2
ss=1.5#мидель стабилизирующего парашюта м2
Cpars=0.35#коэффициент лобового сопротивления стабилизирующего парашюта
S=70#мидель основного парашюта м2
tsp=40# время свободного падения c.
tssp=3 # время падения со стабилизирующим парашютом c.
tpr=210# общее время прыжка в с.
h=4000.0# высота прыжка в м.
V0=100.0#начальная горизонтальная скорость в м/с
beta=1.25*10**-4
alfa=6.5*10**-3
T0=300
def ks(t):
if t<= tsp:
z=0
else:
z=1
return z
def ko(t):
if t<= tsp+tssp:
z=0
else:
z=1
return z
def f(y,t):
y1,y2,y3,y4=y
rou=rou0*exp(-beta*y1*T0/(T0-alfa*y1))
rp=0.5*Cp*rou*s/mp
rpars=0.5*Cpars*rou*ss/mp
rpar=0.5*Cpar*rou*S/mp
return [-y2*sin(y3),g*sin(y3)-rp*(y2**2)-ko(t)*rpar*(y2**2)-ks(t)*rpars*(y2**2),g*cos(y3)/y2,y2*cos(y3)]
t=arange(0,tpr,1)
y0=[h,100,0,0]
[y1,y2,y3,y4]=odeint(f, y0,t, full_output=False).T
plt.figure()
plt.title('Основные этапы прыжка парашютиста с высоты: %s м.. \n Начальная горизонтальная скоростью: %s м/с. \n Скорость приземления : %s м/с'%(h,V0,round(y2[tpr-tsp-tssp],0)))
plt.plot(y1,y2*sin(y3),label='Время свободного падения.: %s c. \n Время падения на стабилизирующем парашюте: %s с. \n Время падения на основном парашюте: %s с. '%(tsp,tssp,tpr-tsp-tssp))
plt.xlabel('Высота в м.')
plt.ylabel('Скорость падения в м/с')
plt.legend(loc='best')
plt.grid(True)
plt.figure()
plt.title("Снос- расстояние в проекции на землю от точки выброса \n до точки приземления")
plt.plot(y1,y4)
plt.xlabel('Высота в м.')
plt.ylabel('Расстояние от точки выброса в м.')
plt.grid(True)
plt.figure()
plt.title("Зависимость скорости падения парашютиста от времени")
plt.plot(t,y2*sin(y3))
plt.xlabel('Время в с.')
plt.ylabel('Скорость паления в м/с.')
plt.grid(True)
plt.show()
Получим:
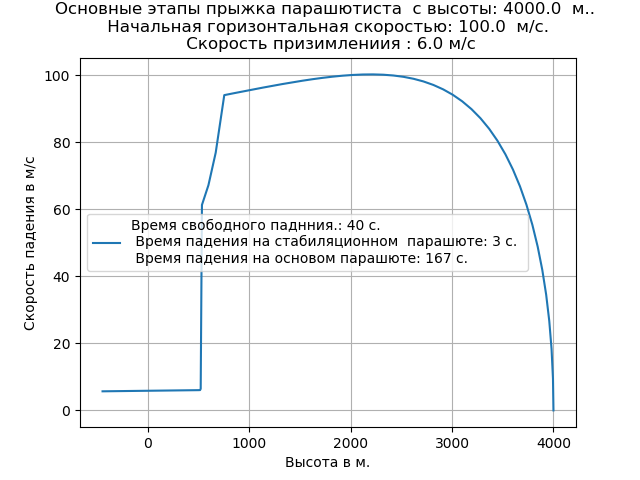
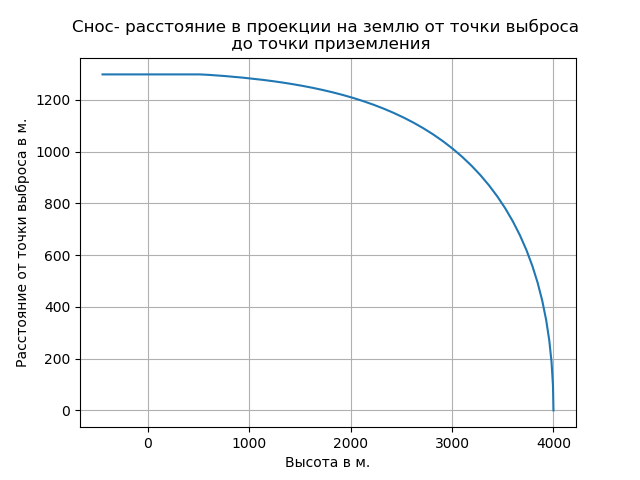
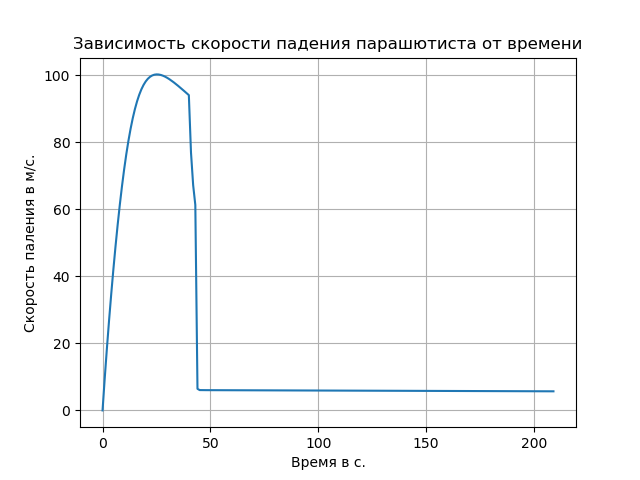
Учёт разрежённости воздуха привёл к увеличению скорости свободного падения и изменил характер траектории на этом участке.
Указанную задачу можно решить и при помощи системы из двух дифференциальных уравнений, которые приводятся ниже (без учёта парашютов и изменения плотности воздуха):
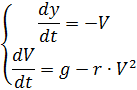
# -*- coding: utf8 -*-
from numpy import*
from scipy.integrate import odeint
import matplotlib.pyplot as plt
m=100
r0=1.3
c1=0.3
c2=0.6
c3=0.5
c4=0.75
S=70
s=0.8
ss=1.5
g=9.8
tsp=6
tsbp=10
tp=90.0
h=1000.0
beta=1.25*10**-4
alfa=6.5*10**-3
T0=300
def ks(t):
if t< tsp:
z=0
else:
z=1
return z
def ko(t):
if t< tsp+tsbp:
z=0
else:
z=1
return z
#dy1/dt=y2
#dy2/dt=g-(k1*y2**2)/m-(k2*y2)/m-(ks(t)*k3*y2**2)/m-(ko(t)*k4*y2**2)/m
def f(y,t):
y1,y2=y
r=r0*exp(-beta*y1*T0/(T0-alfa*y1))
k1=0.5*r*c1*s
k2=0.5*r*c2*s
k3=0.5*r*c3*ss
k4=0.5*r*c4*S
return[-y2,g-(k1*y2**2)/m-(k2*y2)/m-(ks(t)*k3*y2**2)/m-(ko(t)*k4*y2**2)/m]
t = arange(0.0,tp)
y0 = [ h, 0.0]
[y1,y2]=odeint(f, y0,t, full_output=False).T
plt.title(«Прыжки с парашютом с 1000 и 800 метров»)
plt.plot(y1,y2,label='Высота 1000 м')
h=800.0
tsp=6
tsbp=2
tp=80.0
def ks(t):
if t< tsp:
z=0
else:
z=1
return z
def ko(t):
if t< tsp+tsbp:
z=0
else:
z=1
return z
def f(y,t):
y1,y2=y
r=r0*exp(-beta*y1*T0/(T0-alfa*y1))
k1=0.5*r*c1*s
k2=0.5*r*c2*s
k3=0.5*r*c3*ss
k4=0.5*r*c4*S
return[-y2,g-(k1*y2**2)/m-(k2*y2)/m-(ks(t)*k3*y2**2)/m-(ko(t)*k4*y2**2)/m]
t = arange(0.0,tp)
y0 = [ h, 0.0]
[y1,y2]=odeint(f, y0,t, full_output=False).T
plt.plot(y1,y2,label='Высота 800 м')
plt.xlabel('Время в с.')
plt.ylabel('Скорость паления в м/с.')
plt.legend(loc='best')
plt.grid(True)
plt.show()
Получим:
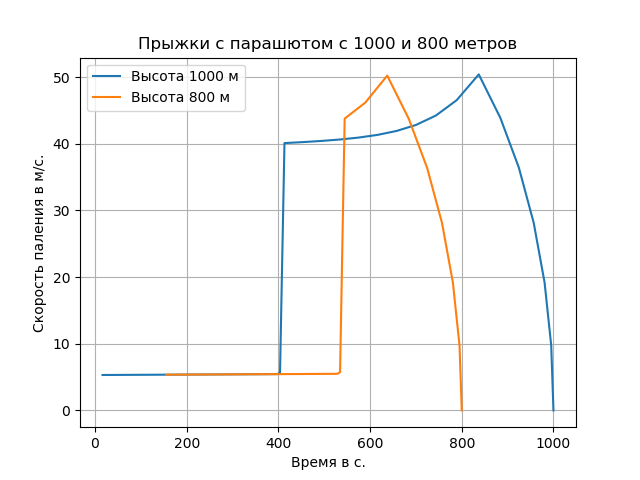
Вывод
Определены баллистико-временные характеристики движения центра масс парашютиста, десантированного с самолёта.
Ссылки
- Атмосферное давление.
- Герасименко И.А. Воздушно-десантная подготовка: учеб. М.: Воениздат, 1986. Ч. 1. С. 32.
The information above is very good to me, thanks for sharing!
ОтветитьУдалить