Рассмотрим самый базовый пример нейронных сетей — перцептроны; я сам только после этого примера полностью осознал, как работают нейронные сети, так что, если я не накосячу, и вы сможете понять. Помните: никакой магии здесь нет, простая математика уровня пятого класса средней школы.
Предположим, у нас есть три разных бинарных условия (да или нет) и одно бинарное решение на выходе (да или нет):

Простая модель с тремя вводными и одним выводом. Эта модель может абсолютно отлично работать для разных людей и выдавать им разные результаты, в зависимости от того, как они обучили нейронную сеть. Но что такое нейронная сеть? Это — просто отдельно стоящие блоки — нейроны, связанные между собой. Давайте создадим простую нейронку из трех нейронов:

То, что вы видите между вводом и выводом — это нейроны. Пока что они ни с чем не связаны, но это и отражает их главную особенность, о которой все забывают сказать: они — это полностью абстрактная шняга. То есть сами нейроны вообще ничего не решают, принимает решение именно то, что мы нарисуем дальше. А пока что запомните: нейроны вообще ничего не делают в нейронке, кроме упорядочивания и упрощения концепта для человека. Давайте нарисуем самую важную часть нейронки — связи:
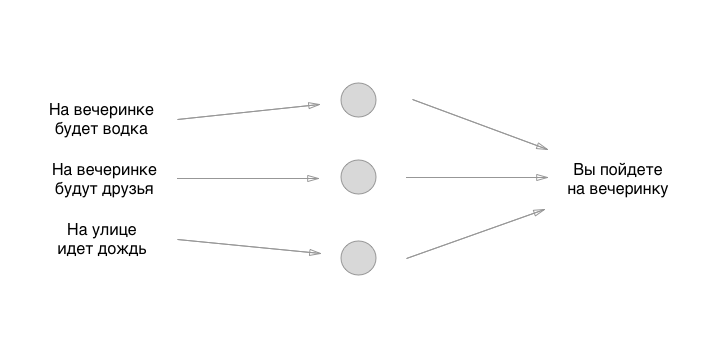
Воу, уже похоже на что-то супер клевое. Сейчас добавим магии, как-то левой пяткой обучим нейронку, покрутимся на месте, похохочем, бросим перца через правое плечо заднего соседа — и все будет работать, да? Оказывается, все еще проще.
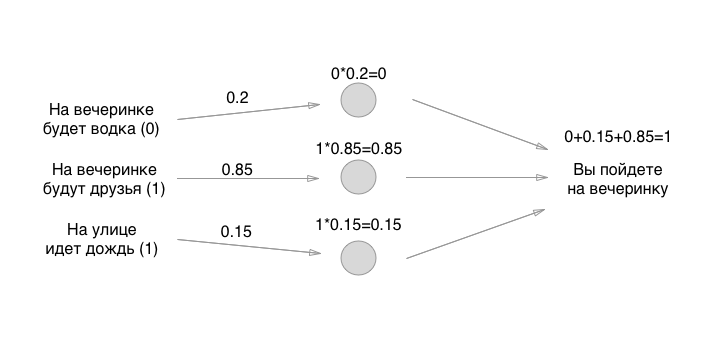
У каждого ввода слева есть значение: 0 или 1, да или нет. Давайте добавим эти значения вводу, предположим, что на вечеринке не будет водки, будут друзья да будет идти дождь:
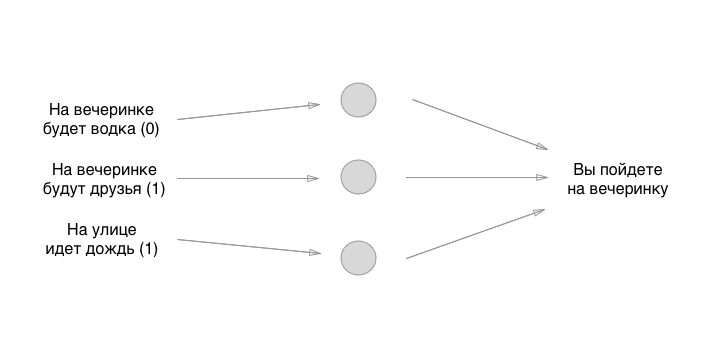
Так, с этим разобрались. Что делаем дальше? А вот тут и возникает веселуха: давайте воспользуемся самым старым способом выставления начального состояния нейронок — великий рандом:
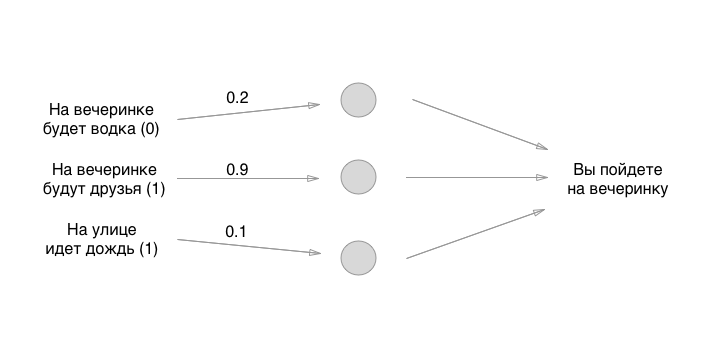
Цифры, которые мы расставили — это веса связей. Помните, что нейроны — это туфта пустая? Так вот, связи — это именно то, из чего и состоит нейронная сеть. Но что за веса связей? Это те штуки, на которые мы умножаем вводные значения и временно храним в пустых нейронах. На самом деле не храним, но для удобства представим, что в нейроны что-то можно положить:
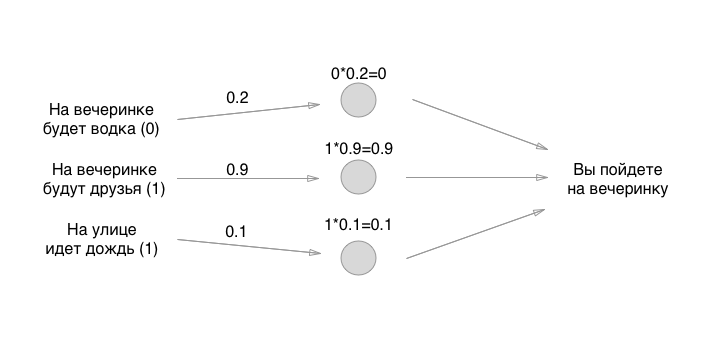
Как вам математика? Смогли произвести умножение? Погодите, самое «сложное» только началось! Дальше мы складываем значения (в одной из реализаций перцептронов):

Ну, вот и все! Нейронка создана, а вы можете ее использовать для любых нужд. Если сумма получается больше 0.5 — идти на вечеринку нужно. Если меньше или равно — на вечеринку идти не нужно. Спасибо за внимание!
Конечно же, модель выше несет в себе мало практической пользы, нам ее нужно обучить. Пугающая фраза «обучить нейронки» — не так ли? Не так. Все топорно и максимально просто: вы берете случайные данные на входе (как мы и сделали), прогоняете ввод через эти три нейрона, смотрите на ответ — пускай он будет положительным (идем на вечеринку) — и проверяете, правильно ли нейронка предугадала ответ или нет. Если правильно — ничего не делаете. Если неправильно — вы слегка сдвигаете веса нейронов (по одному или все сразу) в любую сторону. Например, вот так:
И снова проверяете: ах, что же, опять говорит идти на вечеринку, когда я же не хочу туда идти! И вы снова сдвигаете слегка веса (в ту же сторону, скорее всего) чуть-чуть, и снова проводите эти вводные данные сквозь нейроны, и снова сверяете результат — и либо оставляете веса в покое, либо снова их двигаете. И так триллионы, квадриллионы раз, да со всякими разными вводными данными. У нас тут, конечно, всего 8 комбинаций ввода, но задачи разные бывают (о них чуть ниже).
Вот в этом и заключается основной принцип работы нейронных сетей — как умножение необходимо для дифференциации, так и понимание работы перцептрона нужно для создания и сверточных сетей, и рекурсивных нейронов, и еще какой экзотической дичи.
В итоге, обучив нейронку на решениях, которые принял какой-либо человек, пробежавшись миллиарды раз по ним, перебрав все возможные веса нейронов, вы придете наконец к золотой и оптимальной середине таким образом, что человек введет три начальных значения — а машина прогоняет его по уже стабильной и рабочей формуле с тремя нейронами и выдает ответ.
Единственными тремя неизвестными в нашей были веса связей нейронов, и именно их мы и перебирали. Поэтому я и говорю, что нейроны — это пустышки ничего не решающие, а короли банкета — это веса связей.
Дальше все просто: вместо одного слоя нейронов мы делаем два и снова все перебираем по точно тем же самым принципам, только уже все нейроны отдают значения другим нейронам. Если сначала у нас было только 3 связи, то теперь 3 + 9 связей с весами. А потом три слоя, четыре, рекурсивные слои, зацикленные на себе и тому подобная дичь:
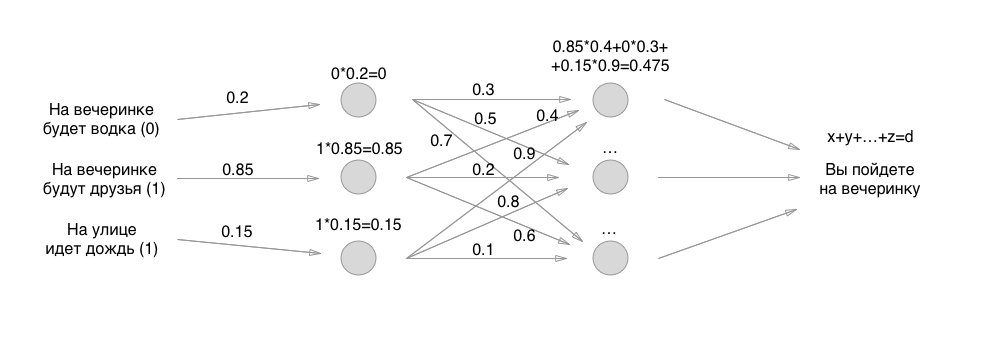
Но, спросите меня, мол, а чего-же в итоге сложного-то в нейронках? Почему так много платят специалистам по машинному обучению? А дело именно в том, как именно реализовывать перцептроны выше: там столько разных ньюансов, что замучаетесь перечислять.
Что, если на входе у вас картинка и нужно категоризировать все картинки на собачек и кошечек? Картинки-то по 512х512 размерам, каждый пиксель ведь ввод — это ж мы сколько по нейронам будем гонять значения? Для этого есть сверточные нейроны! Это такая шняга, которая берет 9 пикселей рядом друг с другом, например, и усредняет их значения RGB. Получается, сжимает картинку для более быстрой обработки. Либо, например, вообще избавляется от красного цвета в картинке, так как он не важен (ищем, например, только зелено-синие платья). Это сверточные сети — дополнительный слой «нейронов» на входе, которые обрабатывают ввод для понятного и упрощенного для сети вида.
Еще нужно понимать, насколько и в какую сторону смещать веса — для этого есть всякие простенькие для понимания алгоритмы, которые считают ошибку с конца — справа (от результата) налево (до первого слоя нейронов) — один из алгоритмов называется Back Propagation.
Еще есть всякие чертовски простые алгоритмы нормализации значений — чтобы у вас на выходе или в середине при сложении получались цифры не от 0 до 500 000, а от 0 до 1 — сильно упрощает расчеты и вычислительную математику.
Как вы уже могли понять, по-настоящему крутые спецы в машинном обучении не просто знают большинство уже существующих методик в постройке оптимизированных нейронных сетей, но и придумывают свои подходы, отталкиваясь от простейшего, но глубокого понимания причинно-следственных связей между тем, как построить перцептрон, и почему это работает, с точки зрения математики. Они могут не просто сделать, чтобы нейронка работала, они могут изменить алгоритм или использовать другой алгоритм, чтобы все еще и быстро, оптимизированно бегало.
Ну, вот и все — я дал вам фундамент для понимания, что такое нейронные сети. Так же я, надеюсь, показал вам, что не так страшен черт, как его малюют — все оказалось невероятно просто, на уровне умножения и сложения. Дальше советую начать смотреть туториалы на YouTube или Udemy — там чуваки офигенно круто все объясняют.
В следующий раз, когда с вас попросят денег на проект с машинным обучением, трясите с попрошаек наброски работы нейронных сетей — какие слои, как они организованы, зачем и почему вот тут так, а там не так. Все это на уровне, максимум, 11 класса будет (это про интегралы и дифференциалы) — и то встретится в описании раз, может, два. Пока этой модели у проекта нет (какие слои и как расположены) — у проекта нет продукта, потому что вот эта структура — это первые 2-4 недели специалиста по машинному обучению.
P.S., пример для объяснения я нагло стянул с одного великолепного видео про нейронные сети. Очень советую посмотреть — спасибо ребятам! подписчики помогли восстановить ссылку на оригинал видео, пример из которого я пытался восстановить из памяти. Если кому интересно, как задачу выше закодить, то приглашаю вас посмотреть вот этот ролик. Спасибо большое авторам!
Комментариев нет:
Отправить комментарий