— Добрый день. Меня зовут Николай, я работаю в компании VisionLabs, которая занимается компьютерным зрением. Наш основной профиль — распознавание лиц, но также у нас есть технологии, которые применимы в дополненной и виртуальной реальности. В частности, у нас есть технология построения 3D-лица по одному фото, и сегодня я буду рассказывать о ней.

Начнем с рассказа о том, что это такое. На слайде вы видите исходную фотографию Джека Ма и 3D-модель, построенную по этой фотографии в двух вариациях: с текстурой и без текстуры, просто геометрию. Это задача, которую мы решаем.

Также мы хотим иметь возможность анимировать эту модель, менять направление взгляда, выражение лица, добавлять мимику и т. д.
Приложение находится в разных областях. Самое очевидное — игры, в том числе VR. Ткже можно делать виртуальные примерочные — примерять очки, бороды и прически. Можно делать 3D-печать, потому что некоторым людям интересны персонализированные аксессуары под их лицо. И можно делать лица для роботов: как печатать, так и показывать на каком-нибудь дисплее на роботе.

Я начну с рассказа о том, как вообще можно генерировать 3D-лица, и потом мы перейдем к задаче 3D-реконструкции как обратной задаче генерации. После этого мы остановимся на анимации и перейдем к челледжам, которые возникают в этой области.

Что такое задача генерации лиц? Нам хотелось бы иметь некоторый способ генерировать трехмерные лица, различающиеся формой и выражением. Здесь два ряда с примерами. Первый ряд показывает лица, отличающиеся формой, принадлежащие как будто разным людям. А снизу одно и то же лицо, имеющее разное выражение.

Один из способов решения задачи генерации — деформируемые модели. Крайнее левое лицо на слайде — некая усредненная модель, к которой мы можем применять деформации с помощью настраивания ползунков. Здесь представлено три ползунка. В верхнем ряду идут лица в сторону увеличения интенсивности ползунка, в нижнем ряду — в сторону уменьшения. Таким образом, мы будем иметь несколько настраиваемых параметров. Устанавливая их, можно придавать лицам разные формы.

Примером деформируемой модели является знаменитая Basel Face Model, построенная из сканов лиц. Чтобы построить деформируемую модель, нужно для начала взять несколько людей, привезти их в специальную лабораторию и отснять их лица специальным оборудованием, переведя их в 3D. Потом на основе этого можно делать новые лица.

Как это устроено математически? Мы можем представить трехмерную модель лица как вектор в 3n-мерном пространстве. Здесь n — количество вершин в модели, каждой вершине соответствует три координаты в 3D, и таким образом мы получаем 3n-координаты.

Если мы имеем набор сканов, то каждый скан представлен таким вектором, и мы имеем набор из n таких векторов.
Далее мы можем строить новые лица как линейные комбинации векторов из нашей базы. При этом нам хотелось бы, чтобы коэффициенты были какие-то осмысленные. Очевидным образом они не могут быть совсем произвольными, и я скоро покажу почему. Одним из ограничений можно установить, чтобы все коэффициенты лежали в промежутке от 0 до 1. Это нужно делать, потому что если коэффициенты будут совсем произвольными, то лица будут получаться неправдоподобные.

Здесь хотелось бы придать параметрам какой-то вероятностный смысл. То есть мы хотим смотреть на набор параметров и понимать, правдоподобное получится лицо или нет. Этим мы хотим добиться того, чтобы искаженным лицам соответствовали низкие вероятности.

Вот как это можно сделать. Мы можем применить метод главных компонент к набору сканов. На выходе мы получим усредненное лицо S0, получим матрицу V, набор главных компонент, а также получим вариации данных вдоль главных компонент. Тогда мы сможем по-новому взглянуть на генерацию лиц, мы будем представлять лица как некоторое усредненное лицо, плюс матрица главных компонент, умноженная на вектор параметров.
Значение параметров — это те самые интенсивности ползунков, о которых я говорил на одном из ранних слайдов. А также мы можем приписать вектору параметров некоторое вероятностное значение. В частности мы можем договориться, чтобы этот вектор был гауссовским.

Таким образом у нас получается метод, который позволяет генерировать 3D-лица, и эта генерация управляется следующими параметрами. Как на предыдущем слайде, мы имеем два набора параметров, два вектора α id и α exp, они такие, как на предыдущем слайде, но α id отвечает за форму лица, а α exp будет отвечать за эмоцию.
Также появляется новый вектор T — вектор текстуры. Он имеет такую же размерность, как вектор формы, и каждой вершине в этом векторе соответствуют три RGB-значения. Аналогичным образом вектор текстуры генерируется с помощью вектора параметров β. Здесь не формализованы параметры, которые будут отвечать за освещение лица и за его положение, но они также существуют.

Вот примеры лиц, которые можно генерировать с помощью деформированной модели. Обратите внимание, что они различаются формой, цветом кожи, а также прорисованы в разных условиях освещения.
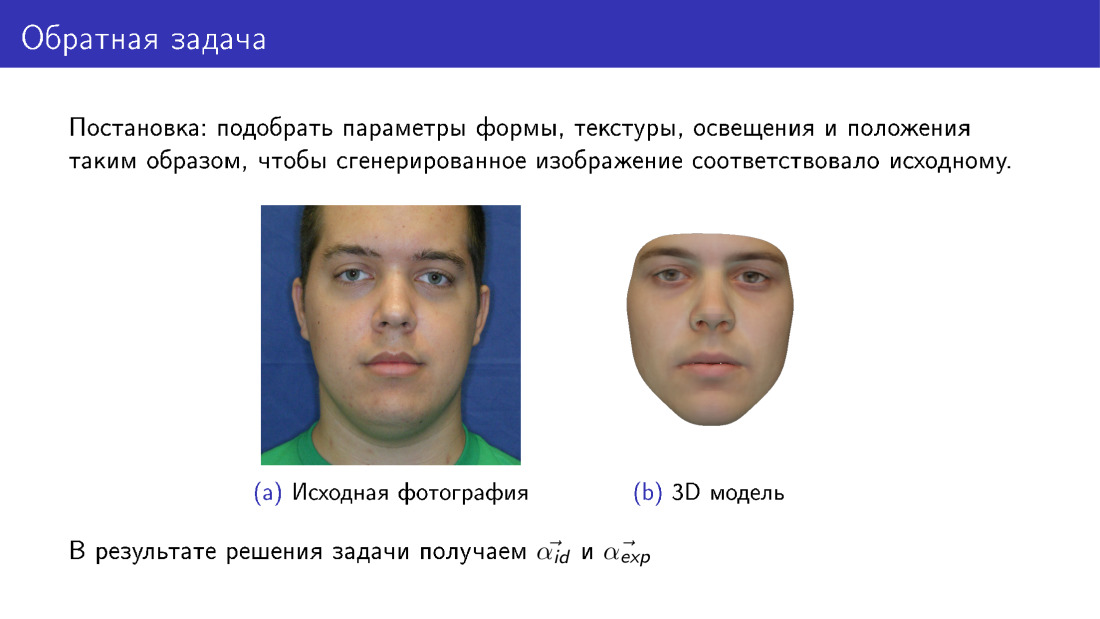
Теперь мы можем перейти к 3D-реконструкции. Это называется обратной задачей, потому что мы хотим подобрать такие параметры для деформируемой модели, чтобы то лицо, которое мы из нее нарисуем, было как можно больше похоже на оригинал. Этот слайд отличается от первого тем, что здесь справа лицо является полностью синтетическим. Если на первом слайде наша текстура была взята из фотографии, то здесь текстура была взята из деформируемой модели.
На выходе мы будем иметь все параметры, на слайде представлены α id и α exp, а также будем иметь освещение, параметры текстуры и т. д.

Мы говорили, что хотим добиться того, чтобы генерируемая модель была похожа на фотографию. Эта похожесть определяется с помощью функции энергии. Здесь мы просто берем попиксельную разность изображений в тех пикселях, где мы считаем, что лицо видно. Например, если лицо будет повернуто, то возникнут перекрытия. Например, часть скулы будет закрыта носом. И матрица видимости M такое перекрытие должна отобразить.
По сути, 3D-реконструкция заключается в минимизации этой функции энергии. Но чтобы эту задачу минимизации решить, было бы хорошо иметь инициализацию и регуляризацию. Регуляризация нужна по понятной причине, как мы говорили, что если мы не будем регуляризировать параметры и делать их совсем уж произвольными, то могут получиться искаженные лица. Инициализация нужна, потому что задача в целом сложная, у нее есть локальные минимумы, и с ними не хочется иметь дела.

Как можно делать инициализацию? Для этого можно использовать 68 ключевых точек лица. Начиная с 2013-2014 года появилось очень много алгоритмов, которые позволяют с довольно хорошей точностью детектировать 68 точек, и сейчас они приближаются к сатурации своей точности. Поэтому мы имеем способ надежно детектировать 68 точек лица.
Мы можем добавить в нашу функцию энергии новое слагаемое, которое будет говорить о том, что мы хотим, чтобы проекции таких же 68 точек модели совпадали с ключевыми точками лица. Мы размечаем эти точки на модели, потом модель как-то деформируем, крутим, проецируя точки, и следим за тем, чтобы положения точек совпадали. На левой фотографии точки двух цветов, фиолетового и желтого. Одни точки были детектированы алгоритмом, а другие — спроецированы из модели. Справа разметка точек на модели, но для точек по краю лица размечена не одна точка, а целая линия. Это сделано, потому что когда лицо поворачивается, разметка этих точек должна измениться, и точка выбирается с линией.

Вот слагаемое, о котором я говорил, оно представляет собой покоординатную разность двух векторов, которые описывают ключевые точки лица и ключевые точки, спроецированные из модели.

Вернемся к регуляризации и рассмотрим всю задачу с позиции Байесовского вывода. Вероятность того, что вектор α равен чему-то заданному при известном изображении пропорциональна произведению вероятности наблюдать изображение при заданном α, помноженная на вероятность α. Если мы возьмем отрицательный логарифм от этого выражения, который мы должны будем свести к минимуму, то мы увидим, что слагаемое, отвечающее за регуляризацию, здесь будет иметь конкретный вид. В частности это второе слагаемое. Вспоминая, что ранее мы сделали предположение, что вектор α гауссовский, мы увидим, что слагаемое, отвечающее за регуляризацию, это сумма квадратов параметров, приведенных к вариациям вдоль главных компонент.

Итак, мы можем выписать полную функцию энергии, содержащую в себе три слагаемых. Первое слагаемое отвечает за текстуру, за разность пикселей между генерируемым изображением и целевым изображением. Второе слагаемое отвечает за ключевые точки, и третье отвечает за регуляризацию.
Коэффициенты при слагаемых в процессе минимизации не оптимизируются, они просто заданы.
Здесь функция энергии представлена как функция всех параметров. α id — параметры формы лица, α exp — параметры выражения, β — параметры текстуры, р — прочие параметры, о которых мы поговрили, но не формализовали их, это параметры положения и освещения.
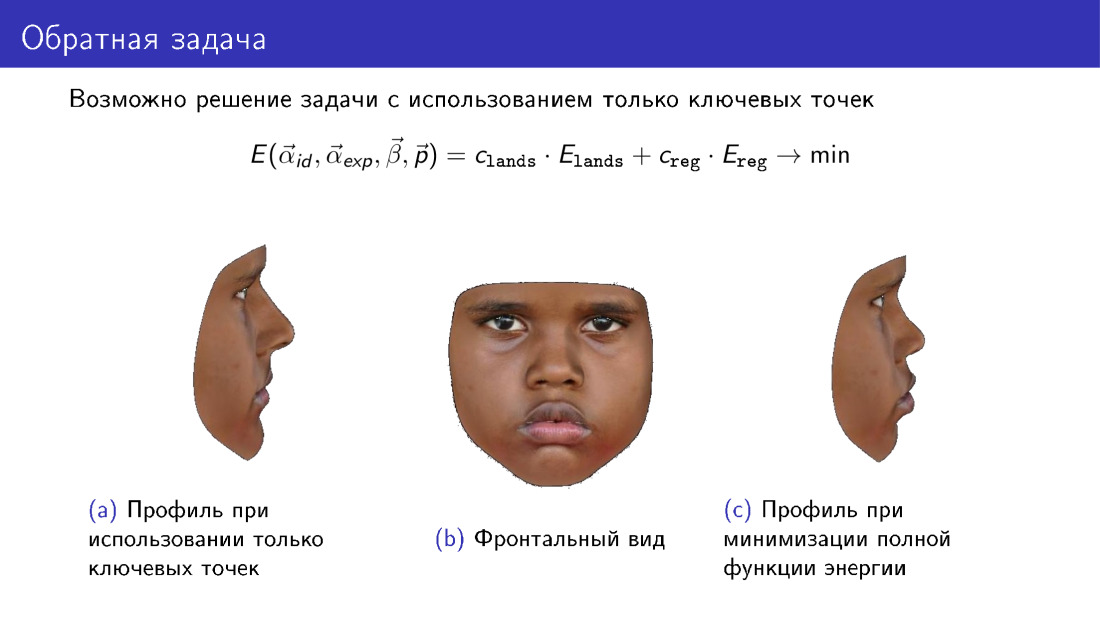
Остановимся на таком замечании. Эту функцию энергии можно упростить. Из нее можно выбросить слагаемое, которое отвечает за текстуру, и использовать только информацию, передаваемую 68 точками. И это позволит построить какую-то 3D-модель. Однако обратите внимание на профиль модели. Слева представлена модель, построенная только по ключевым точкам. Справа представлена модель с использованием текстуры при построение. Обратите внимание, что справа профиль получается более соответствующий центральной фотографии, которая представляет фронтальный вид лица.

Анимация при имеющемся алгоритме построения 3D-модели лица работает достаточно просто. Вспомним, что при построении 3D-модели мы получаем два вектора параметров, один отвечает за форму, другой — за выражение. Эти векторы параметров у пользователя и у аватара всегда будут свои. У пользователя один вектор параметров формы, у аватара он другой. Однако мы можем сделать так, чтобы векторы, отвечающие за выражение, у них стали одинаковы. Мы возьмем параметры, отвечающие за выражение лица пользователя, и просто подставим их в модель аватара. Таким образом мы перенесем выражение лица пользователя на аватар.
Поговорим о двух челеджах в этой области: скорость работы и ограниченность деформируемой модели.

Скорость работы — действительно проблема. Минимизация полной функции энергии очень вычислительноемкая задача. В частности, она может занимать от 20 до 40, в среднем 30 секунд. Это достаточно долго. Если мы будем строить трехмерную модель только по ключевым точкам, получится гораздо быстрее, но от этого пострадает качество.

Как с этой проблемой можно бороться? Можно использовать больше ресурсов, некоторые люди решают эту задачу на GPU. Можно использовать только ключевые точки, но при этом пострадает качество. И можно использовать методы машинного обучения.

Посмотрим по порядку. Вот работа 2016 года, в которой переносится выражение лица пользователя на некоторое заданное видео, вы можете управлять видео с помощью вашего лица. Здесь построение 3D-модели производится в реальном времени с использованием GPU.

Вот методы, которые используют машинное обучение. Идея в том, что мы можем сначала взять большую базу лиц, для каждого лица долгим, но точным алгоритмом построить 3D-модели, каждую модель представить как набор параметров, и дальше обучить сетку эти параметры предсказывать. В частности, в этой работе 2016 года используется ResNet, который на вход берет изображение, а на выход дает параметры модели.

Трехмерную модель можно представлять и по-другому. В этой работе 2017 года 3D-модель представляется не как набор параметров, а как набор вокселей. Сеть предсказывает воксели, превращая картинку в некоторое трехмерное представление. Стоит заметить, что возможны варианты обучения сети, для которых 3D-модели вообще не требуются.

Это работает следующим образом. Здесь наиболее важная часть — слой, который может взять на вход параметры деформируемой модели и срендерить картинку. Он обладает таким замечательный свойством, что через него можно делать обратное распространение ошибки. Сеть принимает на вход изображение, предсказывает параметры, скармливает эти параметры слою, который рендерит изображение, сравнивает это изображение с входным, получает ошибку, делает обратное распространение ошибки и продолжает обучаться. Таким образом сеть учится предсказывать параметры трехмерной модели, имея в качестве обучающих данных только картинки. И это очень интересно.

Мы много говорили о точности — в частности, что она страдает, если мы выбрасываем какие-то слагаемые из функции энергии. Давайте формализуем, что это значит, как можно оценить точность 3D-реконструкции лица. Для этого нужна база ground truth сканов, полученных с помощью специального оборудования, с помощью методов, относительно которых есть какие-то гарантии точности. Если такая база есть, то мы можем наши реконструируемые модели сравнивать с ground truth. Это делается просто: мы считаем среднее расстояние от вершин нашей модели, которую мы построили, до вершин в ground truth, и нормируем на размер скана. Это нужно делать, потому что лица бывают разные, какие-то больше, какие-то меньше, и на маленьком лице ошибка была бы меньше, просто потому что само лицо меньше. Поэтому нужна нормировка.

Я хотел бы рассказать про нашу работу, она будет на воркшопах, есть ECCV. Мы делаем похожие вещи, мы обучаем MobileNet предсказывать параметры деформируемой модели. В качестве обучающих данных мы используем 3D-модели, построенные для фотографий из датасета 300W. Оцениваем точность на базе сканов BU4DFE.
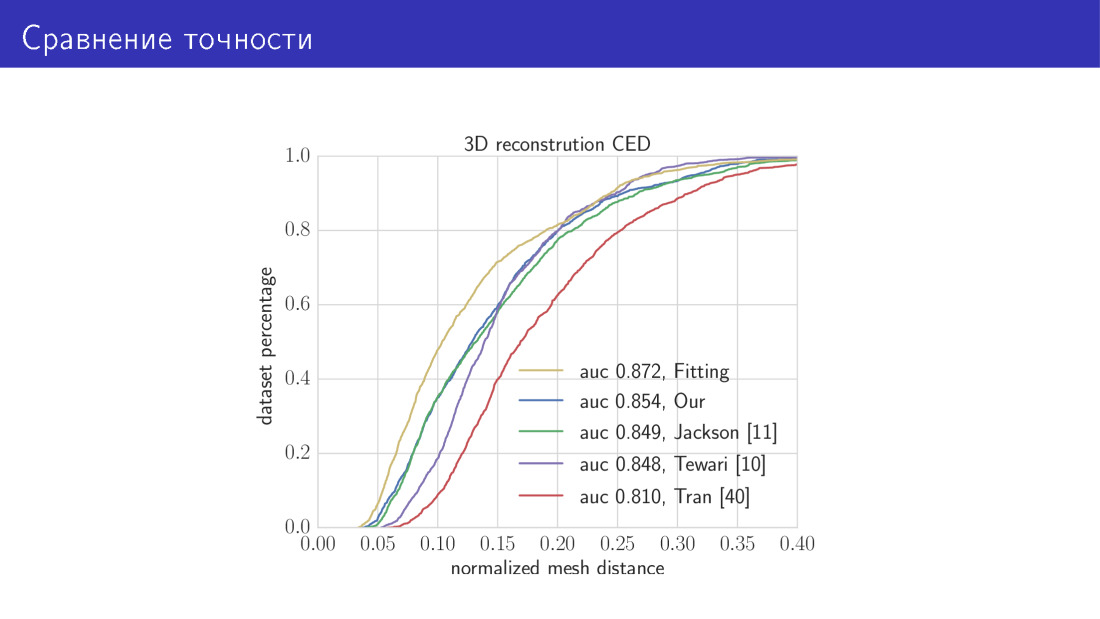
Вот что получается. Мы сравниваем два наших алгоритма с state of the art. Желтая кривая на этом графике — алгоритм, который занимает 30 секунд и заключается в минимизации полной функции энергии. Здесь по оси Х — ошибка, о которой мы только что говорили, среднее расстояние между вершинами. По оси Y — доля изображений, на которых эта ошибка меньше, чем та, что на оси X. На этом графике чем выше кривая, тем лучше. Следующая кривая — наша сеть, основанная на архитектуре MobileNet. Далее три работы, о которых мы говорили. Сеть, предсказывающая параметры, и сеть, предсказывающая воксель.
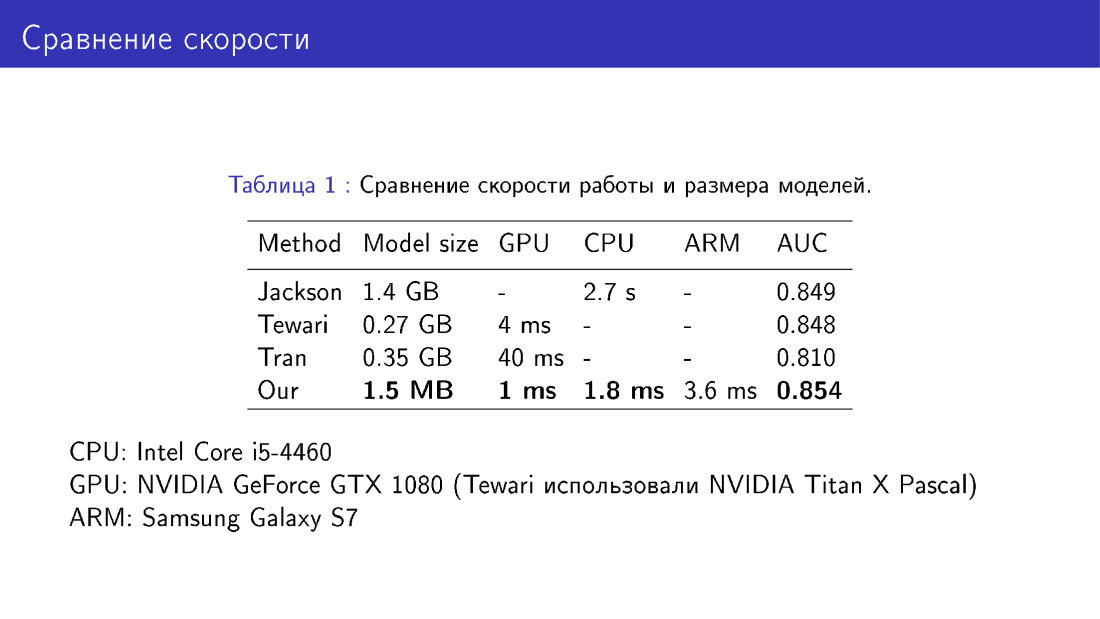
Также мы сравнивали нашу сеть с аналогами в терминах размера модели и скорости работы. Здесь получается выигрыш, поскольку мы используем MobileNet, достаточно легкий.
Второй челендж — ограниченность деформируемой модели.

Обратите внимание на левое лицо, посмотрите на крылья носа. Здесь тени на крыльях носа. Границы теней не совпадают с границами носа на фотографии, таким образом получается дефект. Причиной этого может быть то, что деформируемая модель в принципе не способна построить нос требуемой формы, потому что эта деформируемая модель была получена из сканов всего 200 лиц. Нам хотелось бы, чтобы нос все-таки был правильный, как на правой фотографии. Таким образом, нам нужно за рамки деформируемой модели как-то выйти.

Это можно делать с помощью непараметрической деформации меша. Вот три задачи, которые мы хотели бы решить: модифицировать локальную часть лица, например нос, потом ее встроить в исходную модель лица, да еще и так, чтобы все остальное оставить неизменным.

Это можно делать следующим образом. Вернемся к обозначению меша как вектора в 3n-мерном пространстве и посмотрим на оператор усреднения. Это оператор, который в S с шапкой заменяет каждую вершину на среднее ее соседей. Соседи вершины — это те, что соединены с ней ребром.
Мы определим некоторую функцию энергии, описывающую положение вершины относительно ее соседей. Мы хотим, чтобы положение вершины относительно ее соседей оставалось неизменным или хотя бы менялось не сильно. Но при этом мы будем как-то модифицировать S. Эта функция энергии называется внутренней, потому что также будет присутствовать некоторое внешнее слагаемое, которое будет говорить о том, что, например, нос должен принять заданную форму.
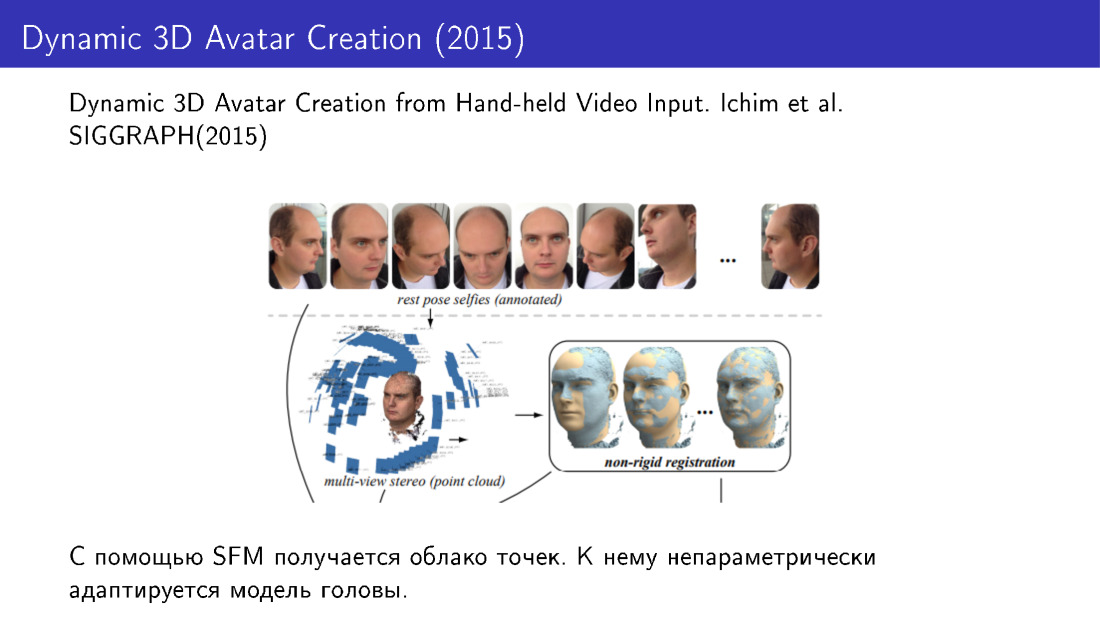
Такие техники применялись, например, в работе 2015 года. Они делали 3D-реконструкцию лиц по нескольким фотографиям. Делали несколько фотографий с телефона, получали облако точек, а дальше адаптировали модель лица к этому облаку с помощью непараметрической модификации.
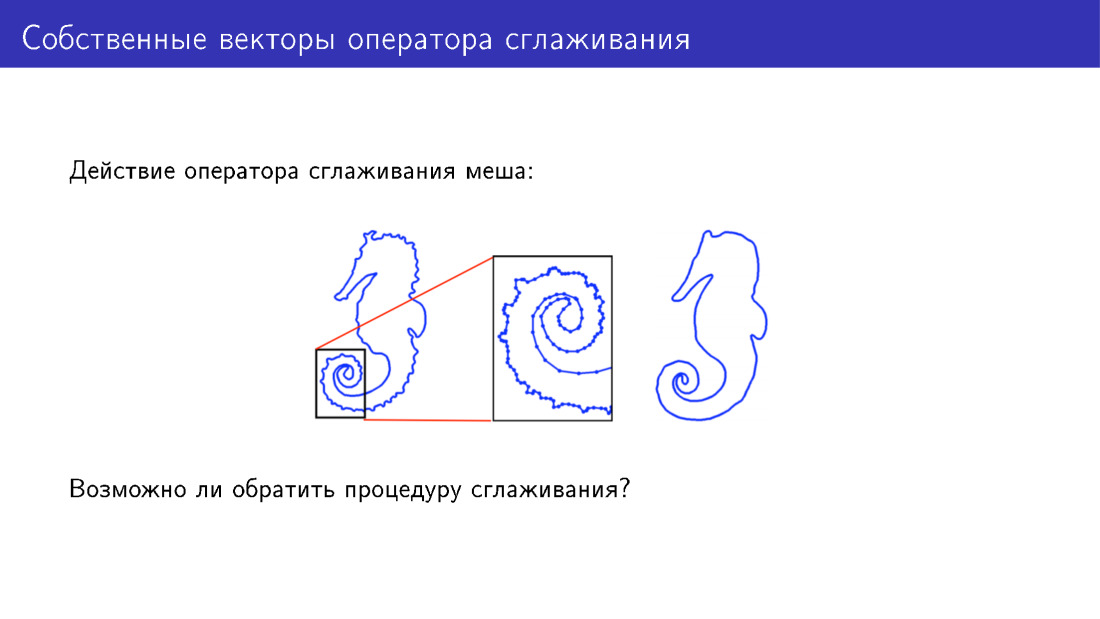
За рамки деформируемой модели можно выйти и другим способом. Остановимся на действии оператора сглаживания. Здесь для простоты представлен двумерный меш, к которому был применен этот оператор. На модели слева есть много деталей, на модели справа эти детали были сглажены. А можем ли мы что-то сделать, чтобы детали добавить, а не убрать?

Для ответа мы можем посмотреть на базис векторов оператора сглаживания. Оператор сглаживания модифицирует коэффициенты меша в разложении по этому базису.
Обязательно ли решать задачу таким образом? Можно делать и по-другому: просто модифицировать эти коэффициенты каким-то внешним образом. Давайте просто возьмем несколько первых векторов оператора сглаживания и добавим его в нашу деформируемую модель как новый набор ползунков. Такая техника действительно позволяет получить улучшения, так делается в работе 2016 года. На этом мой доклад завершается, всем спасибо.
Комментариев нет:
Отправить комментарий