Эта статья познакомит вас с широким диапазоном концепций искусственного интеллекта в играх («игрового ИИ»), чтобы вы понимали, какие инструменты можно использовать для решения задач ИИ, как они работают совместно и с чего можно начать их реализацию в выбранном движке.
Я буду предполагать, что вы знакомы с видеоиграми, немного разбираетесь в таких математических концепциях, как геометрия, тригонометрия и т.д. Большинство примеров кода будет записано псевдокодом, поэтому вам не потребуется знание какого-то конкретного языка.
Игровой ИИ в основном занимается выбором действий сущности в зависимости от текущих условий. В традиционной литературе по ИИ называет это управлением "интеллектуальными агентами". Агентом обычно является персонаж игры, но это может быть и машина, робот или даже нечто более абстрактное — целая группа сущностей, страна или цивилизация. В любом случае это объект, следящий за своим окружением, принимающий на основании него решения и действующий в соответствии с этими решениями. Иногда это называют циклом «восприятие-мышление-действие» (Sense/Think/Act):
- Восприятие: агент распознаёт — или ему сообщают — информацию об окружении, которая может влиять на его поведение (например, находящиеся поблизости опасности, собираемые предметы, важные точки и так далее)
- Мышление: агент принимает решение о том, как поступить в ответ (например, решает, достаточно ли безопасно собрать предметы, стоит ли ему сражаться или лучше сначала спрятаться)
- Действие: агент выполняет действия для реализации своих решений (например, начинает двигаться по маршруту к врагу или к предмету, и так далее)
- … затем из-за действий персонажей ситуация изменяется, поэтому цикл должен повториться с новыми данными.
Задачи ИИ реального мира, особенно те, что актуальны сегодня, обычно сосредоточены на «восприятии». Например, беспилотные автомобили должны получать изображения находящейся перед ними дороги, комбинируя их с другими данными (радара и лидара) и пытаясь интерпретировать то, что они видят. Обычно эта задача решается машинным обучением, которое особо хорошо работает с большими массивами шумных данных реального мира (например с фотографиями дороги перед автомобилем или несколькими кадрами видео) и придаёт им какое-то значение, извлекая семантическую информацию, например «в 20 ярдах передо мной есть ещё одна машина». Такие задачи называются задачами классификации.
Игры необычны тем, что для извлечения этой информации им не нужна сложная система, поскольку она является неотъемлемой частью симуляции. Нет необходимости выполнять алгоритмы распознавания изображений, чтобы обнаружить врага перед собой; игра знает, что там есть враг и может передать эту информацию непосредственно процессу принятия решений. Поэтому «восприятие» в этом цикле обычно сильно упрощено, а вся сложность возникает в реализации «мышления» и «действия».
Игровой ИИ обычно принимает во внимание следующие ограничения:
- В отличие от алгоритма машинного обучения, он обычно не тренируется заранее; при разработке игры непрактично писать нейронную сеть для наблюдения за десятками тысяч игроков, чтобы найти наилучший способ играть против них, потому что игра ещё не выпущена и игроков у неё нет!
- Обычно предполагается, что игра должна развлекать и бросать игроку вызов, а не быть «оптимальной» — поэтому даже если и можно обучить агентов противостоять игрокам наилучшим образом, то чаще всего дизайнерам нужно от них совершенного другое.
- Часто к агентам предъявляют требование «реалистичного» поведения, чтобы игроки ощущали, что соревнуются с человекоподобными противниками. Программа AlphaGo оказалась намного лучше, чем люди, но выбираемые ею ходы настолько далеки от традиционного понимания игры, что опытные противники говорили о ней как об игре против инопланетянина. Если игра симулирует противника-человека, то обычно это нежелательно, поэтому алгоритм нужно настроить таким образом, чтобы он принимал правдоподобные решения, а не идеальные.
- ИИ должен выполняться «в реальном времени». В этом контексте это означает, что алгоритм не может для принятия решения монополизировать ресурсы процессора на длительное время. Даже 10 миллисекунд на принятие решения — это слишком много, потому что большинство игр имеют всего 16-33 миллисекунды на выполнение всех операций для следующего кадра графики.
- В идеале хотя бы часть системы должна зависеть от данных, а не быть жёстко заданной, чтобы не владеющие программированием разработчики могли быстрее вносить изменения.
Узнав всё это, мы можем начать рассматривать чрезвычайно простые подходы к созданию ИИ, которые реализуют весь цикл «восприятие-мышление-действие» способами, обеспечивающими эффективность и позволяющими дизайнерам игры выбирать сложные поведения, похожие на действия человека.
Давайте начнём с очень простой игры, например с Pong. Задача игрока заключается в перемещении «ракетки», чтобы мячик отскакивал от неё, а не пролетал мимо. Правила похожи на теннисные — ты проигрываешь, если пропустил мяч. У ИИ есть относительно простая задача принятия решений о выборе направления движения ракетки.
Жёстко заданные условные конструкции
Если бы мы хотели написать ИИ для управления ракеткой, то существует интуитивно понятное и простое решение — просто постоянно двигать ракетку так, чтобы она находилась под мячом. Когда мяч достигает ракетки, она уже находится в идеальном положении и может отбить его.
Простой алгоритм для этого, выраженный в псевдокоде, может быть таким:
в каждом кадре/обновлении, пока игра выполняется:
если мяч слева от ракетки:
двигать ракетку влево
иначе если мяч справа от ракетки:
двигать ракетку вправо
Если считать, что ракетка может двигаться с не меньшей скоростью, чем мяч, то это будет идеальный алгоритм для ИИ-игрока в Pong. В случаях, когда для обработки есть не так много данных «восприятия» и мало действий, которые может выполнить агент, нам не требуется ничего более сложного.
Этот подход так прост, что в нём едва просматривается весь цикл «восприятие-мышление-действие». Но он есть.
- «Восприятие» — это два оператора «если». Игра знает, где находятся мяч и ракетка. Поэтому ИИ запрашивает у игры их позиции, таким образом «чувствуя», находится ли мяч слева или справа.
- «Мышление» тоже встроено в два оператора «если». В них находится два решения, которые в данном случае взаимно исключают друг друга, приводящие к выбору одного из трёх действий — двигать ракетку влево, двигать её вправо или ничего не делать, если ракетка уже расположена верно.
- «Действие» заключается в конструкциях «двигать ракетку влево» или «двигать ракетку вправо». В зависимости от способа реализации игры это может принимать вид мгновенного перемещения положения ракетки или задания скорости и направления ракетки, чтобы её можно было сдвинуть должным образом в другом коде игры.
Подобные подходы часто называются «реактивными» (reactive), потому что здесь существует простой набор правил (в нашем случае это операторы «если» в коде), который реагирует на состояние мира и мгновенно принимает решение о том, как действовать.
Деревья решений
Этот пример с Pong на самом деле аналогичен формальной концепции ИИ под названием "дерево решений". Это система, в которой решения выстроены в форме дерева и алгоритм должен обходить его, чтобы достичь «листа», содержащего окончательное решение о выбираемом действии. Давайте нарисуем графическое представление дерева решений для алгоритма ракетки Pong с помощью блок-схемы:

Видно, что она напоминает дерево, только перевёрнутое!
Каждую часть дерева решений обычно называют «узлом», потому что в ИИ для описания подобных структур используется теория графов. Каждый узел может быть одного из двух типов:
- Узлы решений: выбор из двух альтернатив на основании проверки какого-то условия. Каждая альтернатива представлена в виде собственного узла;
- Конечные узлы: выполняемое действие, представляющее собой окончательное решение, принимаемое деревом.
Алгоритм начинает с первого узла, назначаемого «корнем» дерева, после чего или принимает решение, в какой дочерний узел перейти на основании условия, или выполняет хранящееся в узле действие, после чего прекращает работу.
На первый взгляд преимущество дерева решений неочевидно, потому что оно выполняет абсолютно ту же работу, что и операторы «если» из предыдущего раздела. Но тут есть очень общая система, в которой каждое решение имеет ровно 1 условие и 2 возможных результата, что позволяет разработчику строить ИИ из данных, представляющих решения в дереве, и избегая жёсткого прописывания его в коде. Легко представить простой формат данных для описания подобного дерева:
| Номер узла | Решение (или «конец») | Действие | Действие |
| 1 | Мяч слева от ракетки? | Да? Проверить узел 2 | Нет? Проверить узел 3 |
| 2 | Конец | Сдвинуть ракетку влево | |
| 3 | Мяч справа от ракетки? | Да? Перейти к узлу 4 | Нет? Перейти к узлу 5 |
| 4 | Конец | Сдвинуть ракетку вправо | |
| 5 | Конец | Ничего не делать | |
С точки зрения кода, нам нужно заставить систему считать каждую из этих строк, создать для каждой узел, прицепить логику решений на основании второго столбца и прицепить дочерние узлы на основании третьего и четвёртого столбцов. Нам по-прежнему нужно вручную жёстко прописывать условия и действия, но теперь мы можем вообразить более сложную игру, в которой можно добавлять новые решения и действия, а также настраивать весь ИИ изменением единственного текстового файла, в котором содержится определение дерева. Мы можем передать файл геймдизайнеру, который получит возможность настраивать поведение без необходимости перекомпиляции игры и изменения кода — при условии, что в коде уже есть полезные условия и действия.
Деревья решений могут быть очень мощными, когда их конструируют автоматически на основе большого множества примеров (например, с помощю алгоритма ID3). Он делает их эффективным и высокопроизводительным инструментом для классификации ситуации на основании входящих данных, но эта тема находится за пределами области создания дизайнерами простых систем выбора действий для агентов.
Скриптинг
Выше мы рассмотрели систему дерева решений, в которой используются заранее созданные условия и действия. Разработчик ИИ может перестраивать дерево любым нужным ему образом, но он должен рассчитывать на то, что программист уже создал все необходимые ему условия и действия. А что, если мы дадим дизайнеру более мощные инструменты, позволяющие ему создавать собственные условия, а может и свои действия?
Например, вместо того, чтобы заставлять кодера писать условия «Мяч слева от ракетки?» и «Мяч справа от ракетки?», он может просто создать систему, в которой дизайнер самостоятельно пишет условия проверки этих значений. В результате данные дерева решений могут выглядеть вот так:
| Номер узла | Решение (или «конец») | Решение | Действие |
| 1 | ball.position.x < paddle.position.x | Да? Проверить узел 2 | Нет? Проверить узел 3 |
| 2 | Конец | Двигать ракетку влево | |
| 3 | ball.position.x > paddle.position.x | Да? Проверить узел 4 | Нет? Проверить узел 5 |
| 4 | Конец | Двигать ракетку вправо | |
| 5 | Конец | Ничего не делать | |
То же самое, что и раньше, но теперь в решениях есть собственный код, похожий на условную часть оператора «если». Код будет считывать из второго столбца узлы решений и вместо поиска конкретного условия (например, «мяч слева от ракетки?»), вычислять условное выражение и возвращать true или false. Это можно реализовать встраиванием скриптового языка, наподобие Lua или Angelscript, который позволяет разработчику брать объекты из игры (например мяч и ракетку) и создавать переменные, доступные из скрипта (например ball.position). На скриптовом языке обычно проще писать, чем на C++, и он не требует полного этапа компиляции, поэтому хорошо подходит для внесения быстрых изменений в логику игры и позволяет менее технически подкованным участникам команды создавать игровые функции без вмешательства кодера.
В показанном выше примере скриптовый язык используется только для вычисления условного выражения, но можно также описывать в скрипте и конечные действия. Например, данные действия вида «двигать ракетку вправо» могут стать конструкцией скрипта наподобие ball.position.x += 10, то есть действие тоже задаётся в скрипте без написания программистом кода функции MovePaddleRight.
Если сделать ещё один шаг вперёд, то можно (и это часто делается) дойти до логического завершения и написать всё дерево решений на скриптовом языке, а не как список строк данных. Это будет код, который похож на показанные выше условные конструкции, только они не «жёстко заданы» — они находятся во внешних файлах скриптов, то есть их можно изменять без рекомпиляции всей программы. Часто даже возможно изменять файл скрипта во время выполнения игры, что позволяет разработчикам быстро тестировать различные подходы к реализации ИИ.
Реакция на события
Показанные выше примеры предназначены для покадрового выполнения в простых играх наподобие Pong. Идея заключается в том, что они непрерывно выполняют цикл «восприятие-мышление-действие» и продолжают действовать на основании последнего состояния мира. Но в более сложных играх вместо вычисления всего чаще разумнее реагировать на «события», то есть на важные изменения в окружении игры.
Это не особо применимо к Pong, поэтому давайте выберем другой пример. Представьте игру-шутер, в которой враги неподвижны, пока не обнаружат игрока, после чего начинают выполнять действия в зависимости от своего класса — рукопашные бойцы могут броситься к игроку, а снайперы остаются на расстоянии и пытаются прицелиться. По сути это является простой реактивной системой — «если видим игрока, то что-то делаем» — но её можно логически разделить на событие («видим игрока») и реакцию (выбираем отклик и выполняем его).
Это возвращает нас к циклу «восприятие-мышление-действие». У нас может быть фрагмент кода, являющийся кодом «восприятия», который проверяет в каждом кадре, видит ли враг игрока. Если нет, то ничего не происходит. Но если он видит, то это создаёт событие «видим игрока». В коде будет отдельная часть, в которой говорится: «когда происходит событие „видим игрока“, то делаем „xyz“», а «xyz» — это любой отклик, которым мы хотим обрабатывать мышление и действие. Для персонажа-бойца можно подключить к событию «видим игрока» отклик «бежать и атаковать». Для снайпера мы подключим к этому событию функцию отклика «спрятаться и прицелиться». Как и в предыдущих примерах, мы можем создавать такие ассоциации в файле данных, чтобы их можно было быстро изменять без пересборки движка. Кроме того, возможно (и это часто используется) писать такие функции откликов на скриптовом языке, чтобы могли создавать сложные решения при возникновении событий.
Хотя простые реактивные системы очень мощны, существует множество ситуаций, когда их недостаточно. Иногда нам нужно принимать разные решения на основании того, чем занимается агент в текущий момент, и представить это в виде условия бывает неудобно. Иногда просто существует слишком много условий, чтобы эффективным образом представить их в виде дерева решений или скрипта. Иногда нам нужно думать заранее и оценивать, как изменится ситуация, прежде чем принимать решение о следующем ходе. Для таких задач нужны более сложные решения.
Конечные автоматы
Конечный автомат (КА, finite state machine, FSM) — это способ сказать иными словами, что какой-то объект — допустим, один из наших ИИ-агентов — в данный момент находится в одном из нескольких возможных состояний, и что он может переходить из одного состояния в другое. Существует конечное количество таких состояний, отсюда и название. Примером из реального мира может служить множество огней светофора, переключающееся с красного на жёлтый, потом на зелёный, и снова обратно. В разных местах есть разные последовательности огней, но принцип одинаков — каждое состояние что-то обозначает («стой», «едь», «стой, если возможно» и т.д.), в любой момент времени существует только одно состояние, а переходы между ними основаны на простых правилах.
Это хорошо применимо к NPC в играх. У охранника могут быть следующие чётко разделённые состояния:
- Патрулирование
- Нападение
- Бегство
И мы можем придумать следующие правила для перехода между состояниями:
- Если охранник видит противника, он нападает
- Если охранник нападает, но больше не видит противника, то возвращается к патрулированию
- Если охранник нападает, но его серьёзно ранили, то он сбегает
Эта схема достаточно проста и мы можем записать её жёстко заданными операторами «если» и переменной, в которой будет храниться состояние охранника и различные проверки — наличие поблизости врагов, уровень здоровья охранника и т.д. Но представьте, что нам нужно добавить ещё несколько состояний:
- Ожидание (между патрулированием)
- Поиск (когда ранее замеченный враг спрятался)
- Бегство за помощью (когда враг замечен, но он слишком силён, чтобы сражаться с ним в одиночку)
И варианты выбора, доступные в каждом состоянии обычно ограничены — например, охранник, вероятно, не захочет искать потерянного из виду врага, если его здоровье слишком мало.
Рано или поздно длинный список «if <x and y but not z> then <p>» становится слишком неуклюжим, и помочь здесь может формализованный подход к реализации состояний и к переходов между ними. Для этого мы рассматриваем все состояния и под каждым состоянием пперечисляем все переходы к другим состояниям вместе с необходимыми для них условиями. Также нам нужно указать исходное состояние, чтобы мы знали, с чего начать, прежде чем применять другие условия.
| Состояние | Условие перехода | Новое состояние |
| Ожидание | ожидал в течение 10 секунд | Патрулирование |
| враг видим и враг слишком силён | Поиск помощи | |
| враг видим и здоровья много | Нападение | |
| враг видим и здоровья мало | Бегство | |
| Патрулирование | завершён маршрут патрулирования | Ожидание |
| враг видим и враг слишком силён | Поиск помощи | |
| враг видим и здоровья много | Нападение | |
| враг видим и здоровья мало | Бегство | |
| Нападение | врага не видно | Ожидание |
| здоровья мало | Бегство | |
| Бегство | врага не видно | Ожидание |
| Поиск | искал в течение 10 секунд | Ожидание |
| враг видим и враг слишком силён | Поиск помощи | |
| враг видим и здоровья много | Нападение | |
| враг видим и здоровья мало | Бегство | |
| Поиск помощи | друг видим | Нападение |
| Начальное состояние: ожидание | ||
Такая схема называется таблицей перехода между состояниями. Она является сложным (и непривлекательным) способом представления КА. По этим данным также можно нарисовать диаграмму и получить сложное графическое представление того, как может выглядеть поведение NPC.

Она ухватывает саму суть принятия решений для агента на основании ситуации, в которой он находится. Каждая стрелка обозначает переход между состояниями, если условие рядом со стрелкой истинно.
При каждом обновлении (или «цикле») мы проверяем текущее состояние агента, просматриваем список переходов и если условие перехода соблюдено, то переходим к новому состоянию. Состояние «Ожидание» проверяет в каждом кадре или цикле, истекло ли время 10-секундного таймера. Если истекло, то оно запускает переход к состоянию «Патрулирование». Аналогичным образом состояние «Нападение» проверяет, не мало ли здоровья у агента, и если это так, то выполняет переход в состояние «Бегство».
Так обрабатываются переходы между состояниями — но как насчёт поведений, связанных с самими состояниями? С точки зрения выполнения самих действий для состояния обычно существует два вида прикрепления действий к КА:
- Действия для текущего состояния выполняются периодически, например, в каждом кадре или «цикле».
- Действия выполняются при переходе от одного состояния к другому.
Пример первого вида: состояние «Патрулирование» в каждом кадре или цикле продолжает перемещать агента по маршруту патрулирования. Состояние «Нападение» в каждом кадре или цикле пытается начать атаку или переместить в позицию, откуда она возможна. И так далее.
Пример второго вида: рассмотрим переход «если враг видим и враг слишком силён → Поиск помощи». Агент должен выбрать, куда двигаться для поиска помощи, и хранить эту информацию так, чтобы состояние «Поиск помощи» знало, куда двигаться. Аналогично, в состоянии «Поиск помощи», когда помощь найдена, агент снова возвращается в состояние «Нападение», но в этот момент он хочет сообщить дружественному персонажу об угрозе, поэтому может существовать действие «сообщить другу об опасности», выполняемое при этом переходе.
И здесь мы снова можем рассмотреть эту систему с точки зрения «восприятия-мышления-действия». Восприятие встроено в данные, используемые логикой переходов. Мышление встроено в переходы, доступные для каждого состояния. А действие выполняется действиями, совершаемыми периодически в состоянии или при переходе между состояниями.
Эта простая система хорошо работает, хотя иногда постоянный опрос условий перехода может быть затратным процессом. Например, если каждому агенту нужно выполнять в каждом кадре сложные вычисления для определения видимости врагов и принятия решения о переходе от патрулирования к нападению, то на это может уходить много процессорного времени. Как мы видели раньше, можно воспринимать важные изменения состояния мира как «события», которые обрабатываются после того, как они произошли. Поэтому вместо того, чтобы в каждом кадре явным образом проверять условие перехода «может ли мой агент увидеть игрока?», мы можем создать отдельную систему видимости, выполняющую эти проверки чуть менее часто (например, 5 раз в секунду), и создающую событие «игрок видим» при срабатывании проверки. Оно передаётся конечному автомату, у которого теперь есть условие перехода «Получено событие „игрок видим“», и которое реагирует на него соответствующим образом. Получившееся поведение будет аналогичным, за исключением едва заметной (и даже увеличивающей реалистичность) задержки реакции, но производительность увеличится благодаря переносу «восприятия» в отдельную часть программы.
Иерархические конечные автоматы
Всё это хорошо, но с большими конечными автоматами становится очень неудобно работать. Если мы хотим расширить состояние «Нападение», заменив его на отдельные состояния «Рукопашная атака» и «Атака издалека», то нам придётся изменять входящие переходы от каждого состояния, настоящего и будущего, которому нужна возможность перехода в состояние «Нападение».
Вероятно, вы также заметили, что в нашем примере есть много дублируемых переходов. Большинство переходов в состоянии «Ожидание» идентичны переходам в состоянии «Патрулирование», и было бы неплохо избежать дублирования этой работы, особенно если мы захотим добавить ещё больше похожих состояний. Будет логично соединить «Ожидание» и «Патрулирование» в какую-нибудь группу «Небоевые состояния», имеющую только один общий набор переходов в боевые состояния. Если мы представим эту группу как состояние, то сможем рассматривать «Ожидание» и «Патрулирование» «подсостояниями» этого состояния, что позволит нам более эффективно описывать всю систему. Пример использования отдельной таблицы переходов для нового небоевого подсостояния:
Основные состояния:
| Состояние | Условие перехода | Новое состояние |
| Небоевые | враг видим и враг слишком силён | Поиск помощи |
| враг видим и здоровья много | Нападение | |
| враг видим и здоровья мало | Бегство | |
| Нападение | врага не видно | Небоевое |
| мало здоровья | Бегство | |
| Бегство | врага не видно | Небоевое |
| Поиск | искал в течение 10 секунд | Небоевое |
| враг видим и враг слишком силён | Поиск помощи | |
| враг видим и здоровья много | Нападение | |
| враг видим и здоровья мало | Бегство | |
| Поиск помощи | друг видим | Нападение |
| Начальное состояние: небоевое | ||
Небоевое состояние:
| Состояние | Условие перехода | Новое состояние |
| Ожидание | ожидал в течение 10 секунд | Патрулирование |
| Патрулирование | завершил маршрут патрулирования | Ожидание |
| Начальное состояние: ожидание | ||
И в виде диаграммы:

По сути это та же система, только теперь здесь есть небоевое состояние, заменяющее «Патрулирование» и «Ожидание», которое само по себе является конечным автоматом с двумя подсостояниями патрулирования и ожидания. Если каждое состояние потенциально может содержать в себе конечный автомат подсостояний (а эти подсостояния тоже могут содержать в себе собственный конечный автомат, и так далее), то у нас получился иерархический конечный автомат (Hierarchical Finite State Machine, HFSM). Группируя небоевые поведения, мы отсекаем кучу излишних переходов, и можем сделать то же самое для любых новых состояний, которые могут иметь общие переходы. Например, если в будущем мы расширим состояние «Нападение» до состояний «Рукопашная атака» и «Атака снарядом», они могут быть подсостояниями, переход между которыми выполняется на основании расстояния до врага и наличия боеприпасов, имеющими общие выходные переходы на основании уровней здоровья и прочего. Таким образом, минимумом дублированных переходов можно представить сложные поведения и подповедения.
Деревья поведений
С помощью HFSM мы получили способность создавать достаточно сложные множества поведений довольно интуитивно понятным способом. Однако сразу заметно, что принятие решений в виде правил переходов тесно связано с текущим состоянием. Во многих играх требуется именно это. А аккуратное использование иерархии состояний позволяет снизить количество дублируемых переходов. Но иногда нам нужны правила, применяемые вне зависимости от текущего состояния, или применяемые почти во всех состояниях. Например, если здоровье агента снизилось до 25%, он может захотеть убежать, вне зависимости от того, находится ли он в бою, или ожидает, или говорит, или находится в любом другом состоянии. Мы не хотим запоминать, что нужно дописывать это условие к каждому состоянию, которое мы, возможно, добавим персонажу в будущем. Чтобы когда дизайнер позже скажет, что хочет изменить пороговое значение с 25% до 10%, нам не пришлось бы перебирать и изменять каждый соответствующий переход.
Идеальной в такой ситуации была система, в которой решения о том, в каком состоянии находиться, существуют отдельно от самих состояний, чтобы мы могли изменить всего лишь один элемент, а переходы всё равно обрабатывались правильно. Именно здесь нам пригодятся деревья поведений.
Существует несколько способов реализации деревьев поведений, но суть для большинства одинакова и очень похожа на упомянутое выше дерево решений: алгоритм начинает работу с «корневого узла», и в дереве есть узлы, обозначающие решения или действия. Однако здесь существуют ключевые отличия:
- Узлы теперь возвращают одно из трёх значений: «успешно» (если работа выполнена), «безуспешно» (если выполнить её не удалось), или «выполняется» (если работа всё ещё выполняется и полностью не закончилась успехом или неудачей).
- Теперь у нас нет узлов решений, в которых мы выбираем из двух альтернатив, а есть узлы-«декораторы», имеющие единственный дочерний узел. Если они «успешны», то выполняют свой единственный дочерний узел. Узлы-декораторы часто содержат условия, определяющие, окончилось ли выполнение успехом (значит, нужно выполнить их поддерево) или неудачей (тогда делать ничего не нужно). Также они могут возвращать «выполняется».
- Выполняющие действия узлы возвращают значение «выполняется», чтобы обозначить происходящие действия.
Небольшой набор узлов можно скомбинировать, создав большое количество сложных поведений, и часто такая схема бывает очень краткой. Например, мы можем переписать иерархический КА охранника из предыдущего примера в виде дерева поведений:

При использовании этой структуры нет необходимости в явном переходе из состояний «Ожидание» или «Патрулирование» в состояния «Нападение» или любые другие — если дерево обходится сверху вниз и слева направо, то правильное решение принимается на основании текущей ситуации. Если враг видим и у персонажа мало здоровья, то дерево завершит выполнение на узле «Бегство», вне зависимости от предыдущего выполненного узла («Патрулирование», «Ожидание», «Нападение» и т.д.).
Можно заметить, что у нас пока нет перехода для возврата в состояние «Ожидание» из «Патрулирования» — и тут нам пригодятся безусловные декораторы. Стандартным узлом-декоратором является «Повтор» (Repeat) — у него нет условий, он просто перехватывает дочерний узел, возвращающий «успешно» и снова выполняет дочерний узел, возвращая «выполняется». Новое дерево выглядит так:

Деревья поведения довольно сложны, потому что часто существует множество различных способов составления дерева, а поиск правильной комбинации декоратора и составляющих узлов может быть хитрой задачей. Существуют также проблемы с тем, как часто нужно проверять дерево (хотим ли мы обходить его каждый кадр или когда происходит что-то, способное повлиять на условия?) и со способом хранения состояния относительно узлов (как мы узнаем, что ждали 10 секунд? Как мы узнаем, сколько узлов было выполнено в последний раз, чтобы правильно завершить последовательность?) Поэтому существует множество разных реализаций. Например, в некоторых системах наподобие системы деревьев поведений Unreal Engine 4 узлы-декораторы заменены на строковые декораторы, которые проверяют дерево только при изменении условий декоратора и предоставляют «сервисы», которые можно подключить к узлам и обеспечивать периодические обновления даже когда дерево не проверяется заново. Деревья поведений — это мощные инструменты, но изучение их правильного использования, особенно с учётом множества разных реализаций, может быть пугающей задачей.
Системы на основе полезности (Utility)
В некоторых играх требуется существование множества различных действий, поэтому им требуются более простые централизованные правила переходов, но при этом не требуется мощь полной реализации дерева поведений. Вместо создания явного набора выборов или дерева потенциальных действий с подразумеваемыми резервными позициями, задаваемыми структурой дерева, возможно, лучше просто исследовать все действия и выбирать то, которое наиболее применимо прямо сейчас?
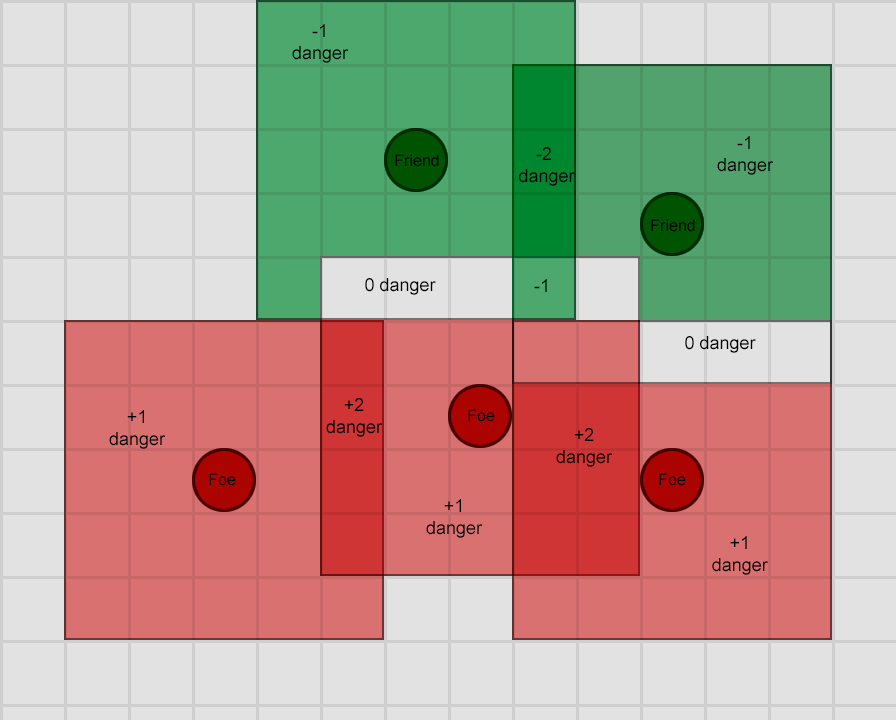
Именно этим и занимается системы на основе полезности — это такие системы, в которых в распоряжении агента есть множество действий, и он выбирает выполнение одного на основании относительной полезности каждого действия. Полезность здесь — это произвольная мера важности или желательности для агента выполнения этого действия. Благодаря написанию функций полезности для вычисления полезности действия на основании текущего состояния агента и его окружения, агент может проверять значения полезности и выбирать наиболее подходящее в данный момент состояние.
Это тоже очень сильно напоминает конечный автомат, за исключением того, что переходы определяются оценкой каждого потенциального состояния, в том числе и текущего. Стоит заметить, что в общем случае мы выбираем переход к наиболее ценному действию (или нахождение в нём, если мы уже выполняем это действие), но для большей вариативности это может быть взвешенный случайный выбор (отдающий приоритет самому ценному действию, но допускающий выбор других), выбор случайного действия из пяти лучших (или любого другого количества), и т.д.
Стандартная система на основе полезности назначает некий произвольный интервал значений полезности — допустим от 0 (совершенно нежелательно) до 100 (абсолютно желательно), а у каждого действия может быть набор факторов, влияющих способ вычисления значения. Возвращаясь к нашему примеру с охранником, можно представить нечто подобное:
| Действие | Вычисление полезности |
| Поиск помощи | Если враг видим и враг силён, а здоровья мало, то возвращаем 100, в противном случае возвращаем 0 |
| Бегство | Если враг видим и здоровья мало, то возвращаем 90, иначе возвращаем 0 |
| Нападение | Если враг видим, возвращаем 80 |
| Ожидание | Если находимся в состоянии ожидания и уже ждём 10 секунд, возвращаем 0, в противном случае 50 |
| Патрулирование | Если находимся в конце маршрута патрулирования, возвращаем 0, в противном случае 50 |
Один из самых важных аспектов этой схемы заключается в том, что переходы между действиями выражены совершенно неявно — из любого состояния можно совершенно законно перейти к любому другому. Кроме того, приоритеты действий подразумеваются в возвращаемых значениях полезности. Если враг видим, и если он силён, а здоровья у персонажа мало, то ненулевые значения возвращают Бегство и Поиск помощи, но Поиск помощи всегда имеет более высокую оценку. Аналогичным образом, небоевые действия никогда не возвращают больше 50, поэтому их всегда побеждает боевое действие. С учётом этого создаются действия и их вычисления полезности.
В нашем примере действия возвращают или постоянное значение полезности, или одно из двух постоянных значений полезности. В более реалистичной системе используется возврат значения из непрерывного интервала значений. Например действие Бегство может возвращать более высокие значения полезности, если здоровье агента ниже, а действие Нападение может возвращать более низкие значения полезности, если враг слишком силён. Это позволит Бегству иметь приоритет перед Нападением в любой ситуации, когда агент чувствует, что ему недостаточно здоровья, чтобы сражаться с врагом. Это позволяет изменять относительные приоритеты действий на основании любого количества критериев, что может сделать такой подход более гибким, чем дерево поведений или КА.
У каждого действия обычно есть несколько условий, влияющих на вычисление полезности. Чтобы не задавать всё жёстко в коде, можно записывать их на скриптовом языке или как серию математических формул, собранных вместе понятным способом. Гораздо больше информации об этом есть в лекциях и презентациях Дэйва Марка (@IADaveMark).
В некоторых играх, которые пытаются моделировать повседневную жизнь персонажа, например, в The Sims, добавляется ещё один слой вычислений, в котором у агента есть «стремления» или «мотивации», влияющие на значения полезности. Например, если у персонажа есть мотивация «Голод», то она со временем может увеличиваться, и вычисление полезности для действия «Поесть» будет возвращать всё более и более высокие значения, пока персонаж не сможет выполнить это действие, снизив уровень голода, а действие «Поесть» снижается до нулевого или околонулевого значения полезности.
Идея выбора действий на основе системы очков достаточно прямолинейна, поэтому очевидно, что можно использовать принятие решений на основе полезности в других процессах принятия решений ИИ, а не заменять их ею полностью. Дерево решений может запрашивать значение полезности своих двух дочерних узлов и выбирать узел с наибольшим значением. Аналогичным образом дерево поведений может иметь композитный узел полезности, который подсчитывает полезность, чтобы выбрать выполняемый дочерний узел.
В наших предыдущих примерах были или простая ракетка, которой мы приказывали двигаться влево-вправо, или персонаж-охранник, которому всегда приказывали патрулировать или нападать. Но как именно нам управлять движением агента в течение промежутка времени? Как нам задавать скорость, избегать препятствий, планировать маршрут, когда до конечной точки нельзя добраться напрямую? Сейчас мы рассмотрим эту задачу.
Steering
На самом простом уровне часто разумно работать с каждым агентом так, как будто у него есть значение скорости, определяющее скорость и направление его движения. Эта скорость может измеряться в метрах в секунду, в милях в час, в пикселях в секунду и так далее. Если вспомнить наш цикл «восприятие-мышление-действие», то можно представить, что «мышление» может выбирать скорость, после чего «действие» прикладывает эту скорость к агенту, перемещая его по миру. Обычно в играх есть система физики, выполняющая эту задачу самостоятельно, изучающая значение скорости каждой сущности и соответствующим образом меняющая позицию. Поэтому часто можно возложить такую работу на эту систему, оставив ИИ только задачу выбора скорости агента.
Если мы знаем, где хочет находиться агент, то нам нужно использовать нашу скорость для перемещения агента в этом направлении. В тривиальном виде у нас получится такое уравнение:
desired_travel = destination_position – agent_position
Представим 2D-мир, в котором агент находится в координатах (-2,-2), а целевая точка — примерно на северо-востоке, в координатах (30, 20), то есть для попадания туда нужно перемещение (32, 22). Давайте будем считать, что эти позиции указаны в метрах. Если мы решим, что агент может двигаться со скоростью 5 м/с, то уменьшим масштаб вектора перемещения до этой величины и увидим, что нам нужно задать скорость примерно (4.12, 2.83). Двигаясь на основании этого значения, агент прибудет в конечную точку чуть менее чем за 8 секунд, как и ожидалось.
Вычисления можно выполнить заново в любой момент времени. Например, если агент находится на полпути к цели, то желательное перемещение будет в два раза меньше, но после масштабирования до максимальной скорости агента в 5 м/с скорость остаётся той же. Это работает и для подвижных целей (в пределах разумного), что позволяет агенту делать небольшие корректировки по ходу движения.
Однако часто нам нужно больше контроля. Например, нам может потребоваться медленно увеличивать скорость, как будто персонаж сначала стоял неподвижно, потом перешёл на шаг, а позже побежал. С другой стороны нам может понадобиться замедлить его, когда он приближается к цели. Часто такие задачи решаются с помощью так называемых "steering behaviours", имеющих собственные названия наподобие Seek, Flee, Arrival и так далее. (На Хабре есть про них серия статей: https://habr.com/post/358366/.) Их идея заключается в том, что к скорости агента можно прикладывать силы ускорения на основании сравнения позиции агента и текущей скорости движения к цели, создавая различные способы движения к цели.
У каждого поведения собственное, слегка отличающееся предназначение. Seek и Arrive служат для движения агента к точке назначения. Obstacle Avoidance и Separation помогают агенту совершать небольшие корректирующие движения для обхода небольших препятствий между агентом и его точкой назначения. Alignment и Cohesion заставляют агентов двигаться вместе, имитируя стадных животных. Любые вариации разных steering behaviours можно сочетать вместе, часто в виде взвешенной суммы, для создания суммарного значения, учитывающего все эти разные факторы и создающего единый результирующий вектор. Например, агент может использовать поведение Arrival вместе с поведениями Separation и Obstacle Avoidance, чтобы держаться подальше от стен и других агентов. Этот подход хорошо работает в открытых окружениях, не слишком сложных и переполненных.
Однако в более сложных окружениях простое сложение выходных значений поведений работает не очень хорошо — иногда движение рядом с объектом происходит слишком медленно, или агент застревает, когда поведение Arrival хочет пройти сквозь препятствие, а поведение Obstacle Avoidance behaviour отталкивает агента в сторону, с которой он пришёл. Поэтому иногда имеет смысл рассмотреть вариации steering behaviours, которые более сложны, чем простое сложение всех значений. Одно из семейств таких подходов заключается в иной реализации — мы рассматриваем не каждое из поведений, дающих нам направление, с последующим их комбинированием для получения консенсуса (который сам по себе может быть неадекватным). Вместо этого мы рассматриваем движение в нескольких различных направлениях — например, в восьми направлениях компаса, или в 5-6 точках перед агентом, после чего выбираем наилучшую.
Тем не менее, в сложных средах с наличием тупиков и вариантов выбора поворотов нам нужно будет что-то более совершенное, и мы вскоре к этому перейдём.
Поиск путей
Steering behaviours отлично подходят для простого движения по достаточно открытой территории, например, футбольному полю или арене, на которой добраться из А в Б можно по прямой линии с небольшими корректировками для избегания препятствий. Но что, если маршрут к конечной точке более сложен? Тогда нам понадобится «поиск путей» (pathfinding) — исследование мира и прокладывание пути по нему для того, чтобы агент попал в конечную точку.
Простейший способ — наложить на мир сетку, и для каждой клетки рядом с агентом смотреть на соседние клетки, в которые мы можем переместиться. Если одна из них является нашей конечной точкой, то пройти маршрут обратно, от каждой клетки к предыдущей, пока не доберёмся до начала, получив таким образом маршрут. В противном случае повторять процесс с достижимыми соседями предыдущих соседей, пока не найдём конечную точку или у нас не кончатся клетки (это будет означать, что маршрута нет). Формально такой подход называется алгоритмом поиска в ширину (Breadth-First Search, BFS), потому что на каждом шаге он смотрит во всех направлениях (то есть «в ширину»), прежде чем переместить поиски наружу. Пространство поиска похоже на волновой фронт, который движется, пока не наткнётся на место, которое мы искали.
Это простой пример поиска в действии. Область поиска расширяется на каждом этапе, пока в неё не будет включена конечная точка, после чего можно отследить путь к началу.

В результате мы получаем список клеток сетки, составляющий маршрут, по которому нужно идти. Обычно он называется «путём», path (отсюда и «поиск путей», pathfinding), но можно его также представить как план, потому что он представляет собой список мест, в которых надо побывать, чтобы достичь своей цели, то есть конечной точки.
Теперь, когда мы знаем позицию каждой клетки в мире, для перемещения по маршруту можно использовать описанные выше steering behaviours — сначала из начального узла к узлу 2, потом от узла 2 к узлу 3, и так далее. Простейший подход заключается в движении к центру следующей клетки, но есть и популярная альтернатива — движение к середине ребра между текущей клеткой и следующей. Это позволяет агенту срезать углы резких поворотов для создания более реалистичного перемещения.
Как можно заметить, этот алгоритм может тратить ресурсы впустую, потому что исследует столько же клеток в «неправильном» направлении, сколько и в «правильном». Также он не позволяет учитывать затраты на перемещение, при которых некоторые клетки могут быть «дороже» других. Здесь нам на помощь приходит более сложный алгоритм под названием A*. Он работает почти так же, как поиск в ширину, только вместо слепого исследования соседей, потом соседей соседей, потом соседей соседей соседей и так далее он помещает все эти узлы в список и сортирует их таким образом, чтобы следующий исследуемый узел всегда был тем, который с наибольшей вероятностью ведёт к кратчайшему маршруту. Узлы сортируются на основании эвристики (то есть, по сути, обоснованного предположения), которая учитывает два аспекта — стоимость гипотетического маршрута до клетки (учитывая таким образом все необходимые затраты на перемещение) и оценку того, насколько далеко эта клетка от конечной точки (таким образом смещая поиск в правильном направлении).

В этом примере мы показали, что он исследует по одной клетке за раз, каждый раз выбирая соседнюю клетку, имеющую наилучшие (или одни из лучших) перспективы. Получающийся путь аналогичен пути поиска в ширину, но в процессе исследовано меньшее количество клеток, и это очень важно для производительности игры на сложных уровнях.
Движение без сетки
В предыдущих примерах использовалась сетка, наложенная на мир, и мы прокладывали маршрут по миру через клетки этой сетки. Но большинство игр не накладывается на сетку, а потому наложение сетки может привести к нереалистичным паттернам движения. Также такой подход может потребовать компромиссов относительно размеров каждой клетки — если она слишком велика, то не сможет адекватно описывать небольшие коридоры и повороты, если слишком маленькая, то поиск по тысячам клеток может оказаться слишком долгим. Какие же есть альтернативы?
Первое, что нам нужно понять — с точки зрения математики сетка даёт нам "граф" соединённых узлов. Алгоритмы A* (и BFS) работают с графами, и им не важна сетка. Поэтому мы можем разместить узлы в произвольных позициях мира, и если между любыми двумя соединёнными узлами есть проходимая прямая линия, а между началом и концом есть хотя бы один узел, то наш алгоритм будет работать как и раньше, и на самом деле даже лучше, потому что узлов станет меньше. Часто это называется системой «точек пути» (waypoints system), поскольку каждый узел обозначает важную позицию мира, которая может создавать часть из любого количества гипотетических путей.

Пример 1: узел в каждой клетке сетки. Поиск начинается с узла, в котором находится агент, и заканчивается конечной клеткой.

Пример 2: гораздо меньшее количество узлов, или точек пути. Поиск начинается с агента, проходит через необходимое количество точек пути и продвигается к конечной точке. Заметьте, что перемещение к первой точке пути к юго-западу от игрока — это неэффективный маршрут, поэтому обычно необходима определённая постобработка сгенерированного пути (например, для того, чтобы заметить, что путь может идти напрямую к точке пути на северо-востоке).
Это довольно гибкая и мощная система, но она требует внимательного расположения точек пути, в противном случае агенты могут и не увидеть ближайшую точку пути, чтобы начать маршрут. Было бы замечательно, если бы могли каким-то образом генерировать точки пути автоматически на основе геометрии мира.
И тут на помощь приходит navmesh. Это сокращение от navigation mesh (навигационный меш). По сути это (обычно) двухмерный меш из треугольников, приблизительно накладывающийся на геометрию мира в тех местах, где игра разрешает перемещаться агенту. Каждый из треугольников в меше становится узлом графа и имеет до трёх смежных треугольников, которые становятся соседними узлами графа.
Ниже представлен пример из движка Unity. Движок проанализировал геометрию мира и создал navmesh (голубого цвета), являющийся аппроксимацией геометрии. Каждый полигон навмеша — это область, в которой может стоять агент, а агент может перемещаться из одного полигона в любой смежный с ним. (В этом примере полигоны сделаны ýже, чем пол, на котором они лежат, чтобы учесть радиус агента, выдающийся за пределы номинальной позиции агента.)

Мы можем выполнить поиск маршрута по мешу, снова воспользовавшись A*, и это даст нам близкий к идеальному маршрут по миру, учитывающий всю геометрию и при этом не требующий избыточного количества лишних узлов (как это было бы с сеткой) и человеческого участия в генерировании точек пути.
Поиск путей — это обширная тема, к которой существует множество подходов, особенно если необходимо программировать низкоуровневые детали самостоятельно. Один из лучших источников дополнительной информации — сайт Амита Патела (перевод статьи на Хабре: https://habr.com/post/331192/).
На примере поиска путей мы увидели, что иногда недостаточно просто выбрать направление и начать двигаться в нём — нам необходимо выбирать маршрут и делать несколько ходов, прежде чем достичь нужной конечной точки. Мы можем обобщить эту идею до широкого набора концепций, в которых цель находится не просто на следующем шаге. Для её достижения необходимо совершить серию шагов, и чтобы знать, каким должен быть первый шаг, может потребоваться заглянуть на несколько шагов вперёд. Такой подход называется планированием. Поиск путей можно считать одним из конкретных применений планирования, но у этой концепции существует гораздо больше областей применения. Если вернуться к циклу «восприятие-мышление-действие», это планирование — это фаза мышления, которая пытается спланировать несколько фаз действия на будущее.
Давайте рассмотрим игру Magic: The Gathering. У вас первый ход, на руках несколько карт, среди которых «Болото», дающее 1 очко чёрной маны, и «Лес», дающий 1 очко зелёной маны, «Чародей-изгнанник», для вызова которого нужно 1 очко синей маны, и «Эльфийский мистик», для вызова которого нужно 1 очко зелёной маны. (Для упрощения мы опустим остальные три карты.) Правила гласят, что игрок может сыграть одну карту земель за ход, может «коснуться» своих карт земель, чтобы получить из них ману, и может произнести столько заклинаний (в том числе и вызова существ), сколько маны у него имеется. В этой ситуации игрок скорее всего сыграет «Лес», коснётся его, чтобы получить 1 очко зелёной маны, а затем вызовет «Эльфийского мистика». Но как игровой ИИ узнает, что нужно принять такое решение?
Простой «планировщик»
Наивный подход может заключаться в простом переборе каждого действия по порядку, пока не останется подходящих. Посмотрев на руку, ИИ видит, что может сыграть «Болото», поэтому так и делает. Остались ли после этого в этом ходу ещё действия? Он не может вызывать ни «Эльфийского мистика», ни «Чародея-изгнанника», потому что для этого нужна зелёная или синяя мана, а сыгранное «Болото» даёт только чёрную ману. И мы не можем сыграть «Лес», потому что уже сыграли «Болото». То есть ИИ-игрок совершит ход по правилам, но он будет не очень оптимальным. К счастью, есть решение получше.
Почти так же, как поиск путей находит список позиций для перемещения по миру с целью попадания в нужную точку, наш планировщик может находить список действий, которые переводят игру в нужное состояние. Также, как каждая позиция на пути имеет набор соседей, являющихся потенциальными вариантами выбора следующего шага по пути, каждое действие в плане имеет соседей, или «наследников», являющихся кандидатами на следующий шаг плана. Мы можем выполнять поиск по этим действиям и наследующим действиям, пока не достигнем желаемого состояния.
Предположим, что для нашего примере желательным результатом будет «вызывать существо, если это возможно». В начале хода у нас есть только два потенциальных действия, разрешённых правилами игры:
1. Сыграть "Болото" (результат: "Болото" уходит из руки и входит в игру) 2. Сыграть "Лес" (результат: "Лес" уходит из руки и входит в игру)
Каждое предпринятое действие может открывать дальнейшие действия или закрывать их, тоже в соответствии с правилами игры. Представьте, что мы выбрали сыграть «Болото» — это закрывает возможность сыграть эту карту как потенциальное наследующее действие (потому что «Болото» уже сыграно), закрывает возможность сыграть «Лес» (потому что правила игры разрешают сыграть только одну карту земель за ход) и добавляет возможность коснуться «Болота» для получения 1 очка чёрной маны — и это, по сути, единственное наследуемое действие. Если мы сделаем ещё один шаг и выберем «коснуться „Болота“», то получим 1 очко чёрной маны, с которым не можем ничего сделать, поэтому это бессмысленно.
1. Сыграть "Болото" (результат: "Болото" уходит из руки и входит в игру)
1.1 Коснуться "Болота" (результат: мы коснулись "Болота", доступно +1 чёрной маны)
Действий не осталось - КОНЕЦ
2. Сыграть "Лес" (результат: "Лес" уходит из руки и входит в игру)
Этот короткий список действий не дал нам многого и привёл к «тупику», если воспользоваться аналогией с поиском путей. Поэтому повторим процесс для следующего действия. Мы выбираем «сыграть „Лес“». Это тоже устраняет возможность «сыграть „Лес“» и «сыграть „Болото“», и открывает в качестве потенциального (и единственного) следующего шага «коснуться „Леса“». Это даёт нам 1 очко зелёной маны, что в свою очередь открывает третий шаг — «вызвать „Эльфийского мистика“».
1. Сыграть "Болото" (результат: "Болото" уходит из руки и входит в игру)
1.1 Коснуться "Болота" (результат: мы коснулись "Болота", доступно +1 чёрной маны)
Действий не осталось - КОНЕЦ
2. Сыграть "Лес" (результат: "Лес" уходит из руки и входит в игру)
2.1 Коснуться "Леса" (результат: мы коснулись "Болота", доступно +1 зелёной маны)
2.1.1 Вызвать "Эльфийского мистика" (результат: "Эльфийский мистик" в игре, доступно -1 зелёной маны)
Действий не осталось - КОНЕЦ
Теперь мы исследовали все возможные действия и действия, следующие из этих действий, найдя план, позволяющий нам вызвать существо: «сыграть „Лес“», «коснуться „Леса“», «вызвать „Эльфийского мистика“».
Очевидно, это очень упрощённый пример, и обычно нужно выбирать наилучший план, а не просто план, удовлетворяющий каким-то критериям (например «вызвать существо»). Обычно можно оценивать потенциальные планы на основании конечного результата или накапливающейся выгоды от использования плана. Например, можно давать себе 1 очко за выложенную карту земель и 3 очка за вызов существа. «Сыграть „Болото“» будет коротким планом, дающим 1 очко, а план «сыграть „Лес“ → коснуться „Леса“ → вызвать „Эльфийского мистика“» даёт 4 очка, 1 за землю и 3 за существо. Это будет самый выгодный план из имеющихся, поэтому следует выбрать его, если мы назначали такие очки.
Выше мы показали, как работает планирование в пределах одного хода Magic: The Gathering, но его можно применить и к действиям в серии ходов (например, «переместить пешку, чтобы дать пространство для развития слону» в шахматах или «побежать в укрытие, чтобы юнит мог в следующем ходу стрелять, находясь в безопасности» в XCOM) или к общей стратегии всей игры (например, «строить пилоны до всех остальных зданий протоссов» в Starcraft, или «выпить зелье Fortify Health перед нападением на врага» в Skyrim).
Улучшенное планирование
Иногда на каждом шагу есть слишком много возможных действий, и оценка каждого варианта оказывается неразумным действием. Вернёмся к примеру Magic: The Gathering — представьте, что у нас на руке есть несколько существ, уже сыграно много земель, поэтому мы можем вызвать любое существо, сыграно несколько существ со своими способностями, а на руке есть ещё пара карт земель — количество перестановок выкладывания земель, использования земель, вызова существ и использования способностей существ может равняться тысячам или даже десяткам тысяч. К счастью, есть пара способов решения этой проблемы.
Первый называется "backwards chaining" («обратный обход»). Вместо проверки всех действий и их результатов мы можем начать с каждого из желательных конечных результатов и посмотреть, сможем ли мы найти к ним прямой путь. Можно сравнить это с попыткой дотянуться до определённого листа на дереве — гораздо логичнее начинать с этого листа и возвращаться назад, прокладывая маршрут по стволу (и этот маршрут мы затем сможем пройти в обратном порядке), чем начинать со ствола и пытаться угадать, какую ветвь выбирать на каждом шагу. Если начинать с конца и идти в обратную сторону, то создание плана окажется намного быстрее и проще.
Например, если у противника осталось 1 очко здоровья, то может быть полезным попытаться найти план «нанести 1 или больше очков прямого урона противнику». Наша система знает, что для достижения этой цели ей нужно скастовать заклинание прямого урона, что в свою очередь означает, что оно должно быть у нас на руке и нам нужно достаточно маны для его произнесения. Это, в свою очередь, означает, что нам нужно коснуться достаточного количества земель для получения этой маны, для чего может потребоваться сыграть дополнительную карту земель.
Ещё один способ — поиск по первому наилучшему совпадению. Вместо длительного обхода всех перестановок мы измеряем, насколько «хорош» каждый частичный план (аналогично тому, как мы выбирали из вариантов планов выше) и вычисляем каждый раз наиболее хорошо выглядящий. Часто это позволяет создать оптимальный, или хотя бы достаточно хороший план без необходимости рассмотрения каждой возможной перестановки планов. A* является разновидностью поиска по первому наилучшему совпадению — сначала он исследует самые многообещающие маршруты, поэтому обычно может найти путь к цели без необходимости забираться слишком далеко в других направлениях.
Интересный и всё более популярный вариант поиска по первому наилучшему совпадению — это поиск по дереву Монте-Карло. Вместо того, чтобы гадать, какие планы лучше других при выборе каждого последующего действия, этот способ выбирает на каждом шаге случайные последующие действия, пока не достигает конца, в котором больше невозможны никакие действия — вероятно, потому что гипотетический план привёл к состоянию победы или проигрышв — и использует этот результат для придания большего или меньшего веса предыдущим выбранным вариантам. При многократном повторении процесса способ может создать хорошую оценку наилучшего следующего шага, даже если ситуация поменяется (например, если противник попытается сорвать наши планы).
Наконец, ни одно обсуждение планирования в играх не будет полным без упоминания планирования действий на основе целей (Goal-Oriented Action Planning, GOAP). Это широко используемая и активно обсуждаемая техника, но если отвлечься от нескольких конкретных деталей реализации, то она по сути является планировщиком обратного обхода, который начинает с цели и пытается подобрать действие, приводящее к этой цели, или, что более вероятно, список действий, приводящий к цели. Например, если целью было «убить игрока» и игрок находится в укрытии, то план может быть таким: «Выкурить игрока гранатой» → «Вытащить оружие» → «Атаковать».
Обычно существует несколько целей, и у каждой есть свой приоритет. Если цели с наивысшим приоритетом достичь не удаётся, например, никакой набор действий не может сформировать план «Убить игрока», потому что игрока не видно, то система возвращается к целям с меньшим приоритетам, например, «Патрулировать» или «Охранять на месте».
В начале статьи мы упомянули, что игровой ИИ в общем случае не использует «машинное обучение», потому что оно обычно не приспособлено для управления в реальном времени интеллектуальными агентами игрового мира. Однако это не значит, что мы не можем позаимствовать что-то из этой области там, где это имеет смысл. Нам может понадобиться, чтобы компьютерный противник в шутере узнал наилучшие места, в которые нужно переместиться, чтобы набрать наибольшее количество убийств. Или мы можем захотеть, чтобы противник в файтинге. например, в Tekken или Street Fighter научился распознавать использование игроком одних и тех же комбо, чтобы начать их блокировать, заставляя игрока применить другую тактику. То есть бывают случаи, когда определённая доля машинного обучения полезна.
Статистика и вероятности
Прежде чем мы перейдём к более сложным примерам, стоит разобраться, насколько далеко мы можем зайти, просто выполняя измерения и используя эти данные для принятия решений. Например, допустим, у нас есть игра в жанре стратегии реального времени, и нам нужно понять, будет ли игрок начинать раш в течение нескольких первых минут, чтобы решить, стоит ли строить больше защиты. Мы можем экстраполировать предыдущее поведение игрока, чтобы понять, каким может быть поведение в будущем. Сначала у нас нет данных, которые можно экстраполировать, но каждый раз, когда ИИ играет против живого противника, он может записывать время первой атаки. Через несколько матчей это время можно усреднить, и мы получим достаточно хорошее приближение времени атаки игрока в будущем.
Проблема с простым усреднением заключается в том, что оно обычно со временем сходится в центре. Поэтому если игрок использовал стратегию раша первые 20 раз, а в следующие 20 раз переключился на гораздо более медленную стратегию, то среднее значение будет где-то посередине, что не даст нам никакой полезной информации. Один из способов улучшения данных — использование простого окна усреднения, учитывающего только последние 20 точек данных.
Похожий подход можно использовать при оценке вероятности совершения определённых действий, если предположить, что предыдущие предпочтения игрока сохранятся и в будущем. Например, если игрок пять раз атаковал фаерболом, два раза молнией и врукопашную всего один раз, то вероятнее всего, что он предпочтёт фаербол в 5 из 8 раз. Экстраполируя из этих данных, мы можем увидеть, что вероятность использования оружия такая: Фаербол=62,5%, Молния=25% Рукопашная=12,5%. Наши ИИ-персонажи поймут, что им лучше найти огнестойкую броню!
Ещё один интересный метод заключается в использовании наивного байесовского классификатора (Naive Bayes Classifier) для исследования больших объёмов входных данных с целью классификации текущей ситуации, чтобы ИИ-агент мог реагировать соответствующим образом. Байесовы классификаторы наверно лучше всего известны благодаря их использованию в спам-фильтрах электронной почты, где они оценивают слова в письме, сравнивают их с теми словами, которые наиболее часто встречались в спаме и нормальных сообщениях в прошлом. На основании этих вычислений они принимают решение о вероятности того, что последнее полученное письмо является спамом. Мы можем сделать что-то подобное, только с меньшим объёмом входных данных. Записывая всю наблюдаемую полезную информацию (например, создаваемые вражеские юниты, используемые заклинания или исследуемые технологии) и отслеживая получившуюся ситуацию (война/мир, стратегия раша/стратегия защиты и т.д.), мы можем подбирать на основании этого подходящее поведение.
При использовании всех этих техник обучения может быть достаточно, а часто и предпочтительно применять их к данным, собранным во время плейтестинга до выпуска игры. Это позволяет ИИ адаптироваться к различным стратегиям, используемым плейтестерами, и не меняться после выпуска игры. ИИ, который адаптируется к игроку после выпуска игры, может в результате стать слишком предсказуемым или даже слишком сложным для победы над ним.
Простая адаптация на основе весов
Давайте сделаем ещё один шаг вперёд. Вместо того, чтобы просто использовать входящие данные для выбора между дискретными заранее прописанными стратегиями, можно изменять набор значений, влияющих на принятие решений. Если мы хорошо понимаем игрового мира и правил игры, то можем сделать следующее:
- Заставить ИИ собирать данные о состоянии мира и ключевых событиях во время игры (как в примере выше);
- Изменять значения или «веса» на основании данных в процессе их сбора;
- Реализовать решения на основании обработки или вычисления этих весов.
Представьте компьютерного агента, который может выбирать комнаты на карте в шутере от первого лица. У каждой комнаты есть вес, определяющий желательность посещения этой комнаты. Изначально все комнаты имеют одинаковое значение. При выборе комнаты, ИИ подбирает её случайным образом, но с влиянием этих весов. Теперь представьте, что когда компьютерного агента убивают, он запоминает, в какой комнате это происходит, и снижает её вес, чтобы в будущем возвращаться в неё с меньшей вероятностью. Аналогично, представьте, что компьютерный агент совершил убийство. Тогда он может увеличить вес комнаты, в которой находится, чтобы поднять её в списке предпочтений. Так что если одна комната становится особенно опасной для ИИ-игрока, то он начинает избегать её в будущем, а если какая-то другая комната позволяет ИИ получить много убийств, то он будет туда возвращаться.
Марковские модели
Что, если бы мы захотели использовать собираемые данные для создания прогнозов? Например, если мы записываем каждую комнату, в которой видим игрока в течение какого-то промежутка времени, то можем резонно прогнозировать, в какую комнату он может двинуться дальше. Отслеживая и текущую комнату, в которой находится игрок, и предыдущую, и записывая эти пары значений, мы можем вычислить, как часто каждая из предыдущих ситуаций ведёт к последующей ситуации, и использовать это знание для прогнозов.
Представим, что есть три комнаты — красная, зелёная и синяя, и что во время сеанса игры мы получили такие наблюдения:
| Первая комната, в которой замечен игрок | Всего наблюдений | Следующая комната | Сколько раз замечен | Процент |
| Красная | 10 | Красная | 2 | 20% |
| Зелёная | 7 | 70% | ||
| Синяя | 1 | 10% | ||
| Зелёная | 10 | Красная | 3 | 30% |
| Зелёная | 5 | 50% | ||
| Синяя | 2 | 20% | ||
| Синяя | 8 | Красная | 6 | 75% |
| Зелёная |
2 | 25% | ||
| Синяя | 0 | 0% |
Количество обнаружений в каждой из комнат достаточно равномерно, поэтому это не даёт нам понимания того, какая из комнат может стать хорошим местом для засады. Данные могут быть искажены тем, что игроки равномерно спаунятся по карте, с равной вероятностью появиться в любой из этих трёх комнат. Но данные о посещении следующей комнаты могут оказаться полезными и помочь нам прогнозировать движение игрока по карте.
Мы сразу можем заметить, что зелёная комната очень привлекательна для игроков — большинство игроков из красной комнаты переходили в зелёную, а 50% игроков, замеченных в зелёной комнате, остаются там при следующей проверке. Также мы можем заметить, что синяя комната — довольно непривлекательное место. Люди редко переходят из красной или зелёной комнат в синюю и похоже, что никто не любит задерживаться в ней долго.
Но данные говорят нам нечто более конкретное — они говорят, что когда игрок находится в синей комнате, то следом за ней он с наибольшей вероятностью выберет красную, а не зелёную. Несмотря на то, что зелёная комната намного популярное для перехода место, чем красная, тенденция немного обратная, если игрок находится в синей комнате. Похоже, что следующее состояние (т.е. комната, в которую он решит переместиться далее) зависит от предыдущего состояния (т.е. от комнаты, в которой он находится сейчас), поэтому эти данные позволяют нам создавать более качественные прогнозы о поведении игроков, чем при независимом подсчёте наблюдений.
Эта идея о том, что мы можем использовать знания о предыдущем состоянии для прогнозирования будущего состояния называется марковской моделью, а подобные примеры, в которых у нас есть точно измеряемые события (например, «в какой комнате находится игрок»), называются цепями Маркова. Поскольку они представляют собой вероятность перехода между следующими друг за другом состояниями, их часто представляют графически в виде конечного автомата, возле каждого перехода которого указывается его вероятность. Ранее мы использовали конечный автомат для представления состояния поведения, в котором находится агент, но эту концепцию можно распространить на всевозможные состояния, связаны они с агентом или нет. В нашем случае состояния обозначают занимаемые агентом комнаты. Это будет выглядеть так:

Это простой подход для обозначения относительной вероятности перехода в различные состояния, который даёт ИИ способность прогнозирования следующего состояния. Но мы можем пойти дальше, создав систему, заглядывающую в будущее на два или более шага.
Если игрок был замечен в зелёной комнате, мы используем данные, говорящие нам, что есть 50-процентная вероятность того, что при следующем наблюдении он всё ещё будет в зелёной комнате. Но какова вероятность того, что он останется в ней и на третий раз? Это не только вероятность того, что он останется в зелёной комнате в течение двух наблюдений (50% * 50% = 25%), но и вероятность того, что он покинет её и вернётся. Вот новая таблица с предыдущими значениями, применёнными к трём наблюдениям: одному текущему и двум гипотетическим в будущем.
| Наблюдение 1 | Гипотетическое наблюдение 2 | Вероятность в процентах | Гипотетическое наблюдение 3 | Вероятность в процентах | Накапливаемая вероятность |
| Зелёная |
Красная | 30% | Красная | 20% | 6% |
| Зелёная | 70% | 21% | |||
| Синяя | 10% | 3% | |||
| Зелёная |
50% | Красная | 30% | 15% | |
| Зелёная | 50% | 25% | |||
| Синяя | 20% | 10% | |||
| Синяя | 20% | Красная | 75% | 15% | |
| Зелёная | 25% | 5% | |||
| Синяя | 0% | 0% | |||
| Всего: | 100% |
Здесь мы видим, что вероятность увидеть игрока в зелёной комнате спустя 2 наблюдения равна 51% — 21% того, что он придёт из красной комнаты, 5% того, что мы увидим игрока посещающим синюю комнату, и 25% того, что он всё время будет оставаться в зелёной комнате.
Таблица — это просто визуальная подсказка, процедура требует всего лишь умножения вероятностей на каждом этапе. Это значит, что мы можем заглядывать далеко в будущее, но с одной значительной оговоркой: мы делаем предположение, что вероятность входа в комнату целиком зависит от того, в какой комнате мы находимся в данный момент. Эта идея о том, что будущее состояние зависит только от текущего, называется марковским свойством. Хотя она позволяет нам использовать такие мощные инструменты, как цепи Маркова, обычно она является только аппроксимацией. Игроки могут принимать решение о посещении комнат на основании других факторов, например, уровня здоровья и количества боеприпасов, и поскольку мы не записываем эту информацию как часть состояния, наши прогнозы будут менее точными.
N-граммы
Давайте вернёмся к нашему примеру с распознаванием комбо в файтинге. Это похожая ситуация, в которой мы хотим спрогнозировать будущее состояние на основании прошлого (чтобы решить, как заблокировать атаку или увернуться от неё), но вместо изучения одного состояния или события, мы будем рассматривать последовательности событий, создающих комбо-движение.
Один из способов сделать это — сохранять каждый ввод игрока (например, удар ногой, удар рукой или блок) в буфер и записывать весь буфер как событие. Представим, что игрок постоянно нажимает удар ногой, удар ногой, удар рукой для использования атаки "Суперкулак смерти", а система ИИ сохраняет весь ввод игрока в буфер и запоминает последние 3 ввода, использованные на каждом шаге.
| Ввод | Уже имеющаяся последовательность ввода | Новая память ввода |
| Удар ногой | Удар ногой | нет |
| Удар рукой | Удар ногой, удар рукой | нет |
| Удар ногой | Удар ногой, удар рукой, удар ногой | Удар ногой, удар рукой, удар ногой |
| Удар ногой | Удар ногой, удар рукой, удар ногой, удар ногой | Удар рукой, удар ногой, удар ногой |
| Удар рукой | Удар ногой, удар рукой, удар ногой, удар ногой, удар рукой | Удар ногой, удар ногой, удар рукой |
| Блок | Удар ногой, удар рукой, удар ногой, удар ногой, удар рукой, блок | Удар ногой, удар рукой, блок |
| Удар ногой | Удар ногой, удар рукой, удар ногой, удар ногой, удар рукой, блок, удар ногой | Удар рукой, блок, удар ногой |
| Удар ногой | Удар ногой, удар рукой, удар ногой, удар ногой, удар рукой, блок, удар ногой, удар ногой | Блок, удар ногой, удар ногой |
| Удар рукой | Удар ногой, удар рукой, удар ногой, удар ногой, удар рукой, блок, удар ногой, удар ногой, удар рукой | Удар ногой, удар ногой, удар рукой |
(В выделенных жирным строках игрок выполняет атаку «Суперкулак смерти».)
Можно посмотреть на все те разы, когда игрок выбирал в прошлом удар ногой, за которым следовал ещё один удар ногой, и заметить, что следующий ввод всегда бывает ударом рукой. Это позволяет ИИ-агенту создать прогноз о том, что если игрок только что выбрал удар ногой, за которым последовал удар ногой, то он скорее всего далее выберет удар рукой, таким образом запустит Суперкулак смерти. Это позволяет ИИ решить выбрать действие, противодействующие этому удару, например блок или уклонение.
Такие последовательности событий называются N-граммами, где N — количество сохраняемых элементов. В предыдущем примере это была 3-грамма, также называемая триграммой, то есть первые 2 элемента используются для прогнозирования третьего. В 5-грамме по первым 4 элементам прогнозируется пятый, и так далее.
Разработчики должны аккуратно выбирать размер N-грамм (иногда называемый порядком). Чем меньше количество, тем меньше требуется памяти, потому что меньше количество допустимых перестановок, но тем меньше сохраняется истории, а значит, теряется контекст. Например, 2-грамма (также называемая «биграммой») будет содержать записи для удар ногой, удар ногой и записи для удар ногой, удар рукой, но никак не может сохранить удар ногой, удар ногой, удар рукой, поэтому не сможет отследить это комбо.
С другой стороны, чем больше порядок, тем больше требуется памяти, и систему скорее всего будет сложнее обучить, ведь у нас будет гораздо больше возможных перестановок, а значит, мы можем никогда не встретить одну и ту же дважды. Например, если есть три возможных ввода (удар ногой, удар рукой и блок) и мы используем 10-грамму, то всего будет почти 60 тысяч различных перестановок.
Модель биграммы по сути является тривиальной цепью Маркова — каждая пара «будущее состояние/текущее состояние» является биграммой и мы можем предсказывать второе состояние на основании первого. Триграммы и большие N-граммы тоже можно рассматривать как цепи Маркова, где все элементы N-граммы, кроме последнего, формируют первое состояние, а последний элемент является вторым состоянием. В нашем примере с файтингом представлена вероятность перехода из состояния удар ногой и удар ногой в состояние удар ногой, затем удар рукой. Воспринимая несколько элементов истории ввода как единый элемент, мы по сути преобразуем последовательность ввода в один фрагмент состояния, что даёт нам марковское свойство, позволяя использовать цепи Маркова для прогнозирования следующего ввода, то есть угадывания того, какое комбо-движение последует далее.
Мы обсудили несколько способов принятия решений, создания планов и прогнозирования, и все они основаны на наблюдениях агента за состоянием мира. Но как нам эффективно наблюдать за всем игровым миром? Выше мы увидели, что способ представления геометрии мира сильно влияет на перемещение по нему, поэтому легко представить, что это верно и для других аспектов игрового ИИ. Как нам собрать и упорядочить всю необходимую информацию оптимальным (чтобы она часто обновлялась и была доступна многим агентам) и практичным (чтобы информацию можно было легко использовать в процессе принятия решений) способом? Как превратить простые данные в информацию или знание? Для разных игр решения могут быть разными, но существует несколько наиболее популярных подходов.
Тэги/метки
Иногда у нас уже имеется огромный объём полезных данных, и единственное, что нам нужно — хороший способ её категоризации и поиска по ней. Например, в игровом мире может быть множество объектов, и часть из них является хорошим укрытием от вражеских пуль. Или, например, у нас есть куча записанных аудиодиалогов, применимых в конкретных ситуациях, и нам нужен способ быстро разобраться в них. Очевидный шаг заключается в добавлении небольшого фрагмента дополнительной информации, который можно использовать для поиска. Такие фрагменты называются тэгами или метками.
Вернёмся к примеру с укрытием; в мире игры может быть куча объектов — ящики, бочки, пучки травы, проволочные заборы. Некоторые из них пригодны для укрытия, например, ящики и бочки, другие нет. Поэтому когда наш агент выполняет действие «Двигаться в укрытие», он должен выполнить поиск объектов поблизости и определить подходящих кандидатов. Он не может просто выполнять поиск по имени — возможно, в игре есть «Crate_01», «Crate_02», вплоть до «Crate_27», и мы не хотим искать все эти названия в коде. Нам не хочется добавлять в код ещё одно название каждый раз, когда художник создаст новую вариацию ящика или бочки. Вместо этого можно искать любые названия, содержащие слово «Crate», но однажды художник может добавить «Broken_Crate» с огромной дырой, непригодный в качестве укрытия.
Поэтому вместо этого мы создадим тэг «COVER» и попросим художников с дизайнерами прикреплять этот тэг ко всем объектам, которые можно использовать для укрытия. Если они добавят тэг ко всем бочкам и (целым) ящикам, то процедуре ИИ достаточно будет найти объекты с этим тэгом, и она будет знать, что объекты подходят для этой цели. Тэг будет работать, даже если объекты позже переименуют, и его можно добавлять к объектам в будущем, не внося в код лишних изменений.
В коде тэги обычно представляются в виде строки, но если все используемые тэги известны, то можно преобразовать строки в уникальные числа для экономии пространства и ускорения поиска. В некоторых движках тэги являются встроенным функционалом, например, в Unity и в Unreal Engine 4, поэтому в них достаточно определиться с выбором тэгов и использовать их по назначению.
Умные объекты
Тэги — это способ внесения дополнительной информации в окружение агента, чтобы помочь ему разобраться в имеющихся вариантах, чтобы запросы наподобие «Найди мне все ближайшие места, за которыми можно укрыться» или «Найди мне всех врагов поблизости, которые могут кастовать заклинания» выполнялись эффективно и с минимальными усилиями работали для новых игровых ресурсов. Но иногда в тэгах не содержится достаточно информации для их полного использования.
Представьте симулятор средневекового города, в котором искатели приключений бродят где захотят, при необходимости тренируются, сражаются и отдыхают. Мы можем расположить в разных частях города тренировочные площадки и присвоить им тэг «TRAINING», чтобы персонажи могли с лёгкостью найти место для тренировок. Но давайте представим, что одно из них — это стрельбище для лучников, а другое — школа волшебников. В каждом из этих случаев нам нужно показывать свою анимацию, потому что под общим названием «тренировок» они представляют различные действия, и не каждый искатель приключений заинтересован в обоих видах тренировок. Можно углубиться ещё больше и создать тэги ARCHERY-TRAINING и MAGIC-TRAINING, отделить друг от друга процедуры тренировок и встроить в каждую разные анимации. Это поможет решить задачу. Но представьте, что дизайнеры позже заявят «Давайте у нас будет школа Робин Гуда, в которой можно учиться стрельбе из лука и бою на мечах»! А потом, когда мы добавим бой на мечах, они просят создать «Академию заклинаний и боя на мечах Гэндальфа». В результате нам придётся хранить для каждого места несколько тэгов и искать разные анимации на основании того, какой аспект тренировок нужен персонажу, и т.д.
Ещё один способ заключается в хранении информации непосредственно в объекте вместе с влиянием, которое она имеет на игрока, чтобы ИИ-актору просто можно было перечислить возможные варианты и выбирать из них в соответствии с потребностями агента. После чего он может перемещаться в соответствующее место, выполнять соответствующие анимации (или любые другие обязательные действия), как это указано в объекте, и получать соответствующее вознаграждение.
| Выполняемая анимация | Результат для пользователя | |
| Стрельбище | Shoot-Arrow | +10 к навыку Archery |
| Школа магии | Sword-Duel | +10 к навыку Swords |
| Школа Робина Гуда | Shoot-Arrow | +15 к навыку Archery |
| Sword-Duel | +8 к навыку Swords | |
| Академия Гэндальфа | Sword-Duel | +5 к навыку Swords |
| Cast-Spell | +10 к навыку Magic |
У персонажа-лучника рядом с этими 4 локациями будет 6 вариантов, 4 из которых неприменимы к нему, если он не пользуется ни мечом, ни магией. Сопоставляя с результатом в этом случае улучшение навыка, а не название или тэг, мы можем с лёгкостью расширять возможности мира новыми поведениями. Для отдыха и утоления голода можно добавлять гостиницы. Можно позволить персонажам ходить в библиотеку и читать о заклинаниях и об улучшенных техниках стрельбы из лука.
| Название объекта | Выполняемая анимация | Конечный результат |
| Гостиница |
Buy | -10 к голоду |
| Гостиница | Sleep | -50 к усталости |
| Библиотека | Read-Book | +10 к навыку Spellcasting |
| Библиотека | Read-Book | +5 к навыку Archery |
Если у нас уже есть поведение «тренироваться стрельбе из лука», то даже если мы пометим библиотеку как место для ARCHERY-TRAINING, то нам скорее всего понадобится особый случай для обработки анимации «read-book» вместо обычной анимации боя на мечах. Эта система даёт нам бОльшую гибкость, перемещая эти ассоциации в данные и храня данные в мире.
Существование объектов или локаций — библиотеки, гостиницы или школ — сообщает нам о предлагаемых ими услугах, о персонаже, который может их получить, позволяет использовать небольшое количество анимаций. Возможность принятия простых решений о результатах позволяет создавать разнообразие интересных поведений. Вместо того, чтобы пассивно ждать запроса, эти объекты могут предоставлять множество информации о том, как и зачем их использовать.
Кривые реакций
Часто встречается ситуация, когда часть состояния мира можно измерить как непрерывное значение. Примеры:
- «Процент здоровья» обычно имеет значения от 0 (мёртв) до 100 (абсолютно здоров)
- «Расстояние до ближайшего врага» изменяется от 0 до некоторого произвольного положительного значения
Кроме того, в игре может быть некий аспект системы ИИ, требующий ввода непрерывных значений в каком-то другом интервале. Например, для принятия решения о бегстве системе оценки полезности может потребоваться и расстояние до ближайшего врага, и текущее здоровье персонажа.
Однако система не может просто сложить два значения состояния мира, чтобы получить некий уровень «безопасности», потому что эти две единицы измерения несравнимы — систем будет считать, что почти мёртвый персонаж в 200 метрах от врага находится в такой же безопасности, что и абсолютно здоровый персонаж в 100 метрах от врага. Кроме того, в то время как процентное значение здоровья в широком смысле линейно, расстояние таким не является — разница в расстоянии от врага 200 и 190 метров менее значимо, чем разница между 10 метрами и нулём.
В идеале нам нужен такое решение, которое брало бы два показателя и преобразовывало их в похожие интервалы, чтобы их можно было сравнивать непосредственно. И нам нужно, чтобы дизайнеры могли управлять способом вычисления этих преобразований, чтобы контролировать относительную важность каждого значения. Именно для этого используются кривые реакций (Response Curves).
Проще всего объяснить кривую реакции как график с вводом по оси X, произвольные значения, например «расстояние до ближайшего врага» и вывод по оси Y (обычно нормализованное значение в интервале от 0.0 до 1.0). Линия или кривая на графике определяет привязку ввода к нормализованному выводу, а дизайнеры настраивают эти линии, чтобы получить нужное им поведение.
Для вычисления уровня «безопасности» можно сохранить линейность значений процентов здоровья — например, на 10% больше здоровья — это обычно хорошо и когда персонаж тяжело ранен, и когда он ранен легко. Поэтому мы привяжем эти значения к интервалу от 0 до 1 прямолинейно:

Расстояние до ближайшего врага немного отличается, поэтому нас совершенно не волнуют враги за пределами определённого расстояния (допустим 50 метров), и нас гораздо больше интересуют различия на близком расстоянии, чем на дальнем.
Здесь мы видим, что выходные данные «безопасности» для врагов в 40 и в 50 метрах почти одинаковы: 0.96 и 1.0.

Однако между врагом в 15 метрах (примерно 0.5) и врагом в 5 метрах (примерно 0.2) есть гораздо бОльшая разница. Такой график лучше отражает важность того, что враг становится ближе.
Нормализовав оба этих значения в интервале от 0 до 1, мы можем вычислить общее значение безопасности как среднее от этих двух входных значений. Персонаж с 20% здоровья и врагом в 50 метрах будет иметь показатель безопасности 0.6. Персонаж с 75% здоровья и врагом всего в 5 метрах будет иметь показатель безопасности 0.47. А тяжелораненый персонаж с 10% здоровья и врагом в 5 метрах будет иметь показатель безопасности всего 0.145.
Здесь следует учесть следующее:
- Обычно для комбинирования выходных значений кривых реакции в конечное значение используют взвешенное среднее — это упрощает повторное использование тех же кривых для вычисления других значений благодаря применению в каждом случае разных весов, отражающих важность разности.
- Когда входное значение находится за пределами заданного интервала — например, враг дальше, чем в 50 метрах — входное значение обычно ограничивается максимумом интервала, чтобы вычисления производились так, как будто он находится в интервале.
- Реализация кривой реакции часто принимает форму математического уравнения, обычно применяющего (иногда ограниченный интервалом) ввод к линейному уравнению или к простому многочлену. Но может быть достаточно и любой системы, позволяющей дизайнеру создавать и вычислять кривую — например, объект Unity AnimationCurve позволяет подставлять произвольные значения, выбирать плавность линии между значениями и вычислять любую точку на линии.
Blackboards
Часто мы оказываемся в ситуации, когда ИИ для агента должен начать отслеживать знания и информацию, получаемые во время игры, чтобы можно было использовать их при дальнейшем принятии решений. Например, агенту может потребоваться запомнить, на какого последнего персонажа он нападал, чтобы на короткое время сосредоточиться на атаках этого персонажа. Или он должен запоминать, сколько времени прошло после того, как он услышал шум, чтобы через определённый промежуток времени перестать искать его причины и вернуться к прежним занятиям. Очень часто система записи данных сильно отделена от системы считывания данных, поэтому она должна быть легко доступна из агента, а не встроена непосредственно в различные системы ИИ. Считывание может происходить спустя какое-то время после записи, поэтому данные нужно где-то хранить, чтобы их можно было извлечь позже (а не вычислять по требованию, что может быть нереализуемо).
В жёстко заданной кодом системе ИИ решение может заключаться в добавлении необходимых переменных в процессе появления необходимости. Эти переменные относятся к экземплярам персонажа или агента, или встраиваясь в него непосредственно, или создавая отдельную структуру/класс для хранения такой информации. Процедуры ИИ можно адаптировать для считывания и записи этих данных. В простой системе это сработает хорошо, но при добавлении всё большего количества информации она становится громоздкой, и обычно требует каждый раз пересборки игры.
Более совершенный подход заключается в превращении хранилища данных в некую структуру, позволяющую системам считывать и записывать произвольные данные. Такое решение позволяет добавлять новые переменные без необходимости изменения структуры данных, обеспечивая таким образом возможность увеличения количества изменений, которые можно произвести из файлов данных и скриптов без необходимости пересборки. Если у каждого агента хранится просто список пар «ключ-значение», каждая из которых является отдельным фрагментом знания, то различные системы ИИ могут сотрудничать, добавляя и считывая эту информацию при необходимости.
В разработке ИИ такие подходы называются «blackboards» («школьными досками»), потому что каждый участник — в нашем случае это процедуры ИИ (например, восприятие, поиск пути и принятие решений) — могут выполнять запись на «доску», считывать с которой данные для выполнения своей задачи могут любые другие участники. Можно представить это как команду специалистов, собравшихся вокруг доски и записывающих на неё что-то полезное, чем нужно поделиться с группой. При этом они могут читать предыдущие записи своих коллег, пока не придут к совместному решению или плану. Жёстко заданный в коде список общих переменных иногда называется «static blackboard» (потому что элементы, в которых хранится информация, постоянны во время выполнения программы), а произвольный список пар «ключ-значение» часто называют «dynamic blackboard». Но используются они примерно одинаково — как промежуточное звено между частями системы ИИ.
В традиционном ИИ упор обычно делается на сотрудничество различных систем для совместного принятия решения, но в игровом ИИ присутствует относительно малое количество систем. Однако определённая степень сотрудничества всё равно может присутствовать. Представим в экшн-RPG следующее:
- Система «восприятия» регулярно сканирует область и записывает на blackboard следующие записи:
- «Ближайший враг»: «Гоблин 412»
- «Расстояние до ближайшего врага»: 35.0
- «Ближайший друг»: «Воин 43»
- «Расстояние до ближайшего друга»: 55.4
- «Время последнего замеченного шума»: 12:45pm
- «Ближайший враг»: «Гоблин 412»
- Системы наподобие боевой системы могут записывать в blackboard данные времени совершения ключевых событий, например:
- «Время последнего полученного урона»: 12:34pm
Многие из этих данных могут выглядеть избыточными — в конце концов, всегда можно получить расстояние до ближайшего врага, просто зная, кто этот враг, и выполнив запрос его позиции. Но при повторении по несколько раз за кадр для того, чтобы решить, угрожает что-то агенту или нет, это становится потенциально медленной операцией, особенно если ей нужно выполнять пространственный запрос для определения ближайшего врага. А метки времени «последнего замеченного шума» или «последнего полученного урона» всё равно не удастся получить мгновенного — необходима запись времени совершения этих событий, и удобным местом для этого является blackboard.
В Unreal Engine 4 используется система dynamic blackboard для хранения данных, передаваемых деревьями поведений. Благодаря этому общему объекту данных дизайнеры могут с лёгкостью записывать новые значения в blackboard на основании своих блюпринтов (визуальных скриптов), а дерево поведений может позже считывать эти значения для выбора поведения, и для всего этого не требуется рекомпиляция движка.
Карты влияния (Influence Maps)
Стандартной задачей в ИИ является принятие решения о том, куда должен двигаться агент. В шутере мы можем выбрать действие «Двигаться в укрытие», но как решить, где находится укрытие в условиях перемещения врагов? Аналогично с действием «Бегство» — куда безопаснее всего бежать? Или в RTS нам может понадобиться, чтобы отряды атаковали слабое место в обороне противника — как нам определить, где находится это слабое место?
Все эти вопросы можно считать географическими задачами, потому что мы задаём вопрос о геометрии и форме окружения и положении в нём сущностей. В нашей игре все эти данные скорее всего уже имеются, но придать им смысл — непростая задача. Например, если мы хотим найти слабое место в обороне врага, то простой выбор позиции самого слабого здания или укрепления недостаточно хорош, если по флангам у них расположились две мощные орудийные системы. Нам нужен способ, позволяющий учесть локальную область и дающий лучший анализ ситуации.
Именно для этого предназначена структура данных «карта влияния». Она описывает «влияние», которое может оказывать сущность на область вокруг неё. Комбинируя влияние нескольких сущностей, мы создаём более реалистичный взгляд на весь ландшафт. С точки зрения реализации мы аппроксимируем игровой мир, накладывая на него 2D-сетку, и после определения того, в какой клетке сетки находится сущность, мы применяем к этой и окружающим её клеткам оценку влияния, обозначающую тот аспект геймплея, который мы хотим смоделировать. Для получения полной картины мы накапливаем эти значения в той же сетке. После чего мы можем выполнять различные запросы к сетке, чтобы понять мир и принять решение о позиционировании и целевых точках.
Возьмём для примера «самую слабую точку в обороне противника». У нас есть защитная стена, на атаку которой мы хотим отправить пехотинцев, но за ней стоят 3 катапульты — 2 близко друг к другу слева, 1 справа. Как нам выбрать хорошую позицию для атаки?
Для начала мы можем назначить всем клеткам сетки в пределах атаки катапульты +1 очков защиты. Нанесение этих очков на карту влияния для одной катапульты выглядит так:

Голубой прямоугольник ограничивает все клетки, в которых можно начать атаку на стену. Красными квадратами обозначено +1 влияния катапульт. В нашем случае это означает область их атаки и угрозу для нападающих юнитов.
Теперь мы добавим влияние второй катапульты:
У нас появилась тёмная область, в которой влияние двух катапульт складывается, что даёт этим клеткам +2 защиты. Клетка +2 внутри голубой зоны может быть особо опасным местом для атаки стены! Добавим влияние последней катапульты:

[Значки: CC-BY: https://game-icons.net/heavenly-dog/originals/defensive-wall.html]
Теперь у нас есть полное обозначение области, закрываемой катапультами. В потенциальной зоне атаки есть одна клетка, имеющая +2 влияния катапульт, 11 клеток с +1 влияния, и 2 клетки с 0 влияния от катапульт — это основные кандидаты позиции для атаки, в них мы можем атаковать стену, не опасаясь огня катапульт.
Преимущество карт влияния в том, что они преобразуют непрерывное пространство с почти бесконечным множеством возможных позиций в дискретное множество приблизительных позиций, относительно которых мы очень быстро можем принимать решения.
Однако мы получили это преимущество только благодаря выбору небольшого количества потенциальных позиций для атаки. Зачем нам использовать здесь карту влияния вместо того, чтобы проверять вручную расстояние от каждой катапульты до каждой из этих позиций?
Во-первых, вычисление карты влияния может быть очень малозатратным. После того, как на карту нанесены очки влияния, её не нужно менять, пока сущности не начнут двигаться. Это значит, что нам не нужно постоянно выполнять вычисления расстояний или итеративно опрашивать каждый возможный юнит — мы «запекаем» эту информацию в карту и можем передавать запросы к ней любое количество раз.
Во-вторых, мы можем накладывать друг на друга и комбинировать разные карты влияния для выполнения более сложных запросов. Например, чтобы выбрать безопасное место для побега, мы можем взять карту влияния наших врагов и вычесть карту наших друзей — клетки сетки с самым большим отрицательным значением будут считаться безопасными.

Чем краснее, тем опаснее, а чем зеленее, тем безопаснее. Области, в которых влияние накладывается друг на друга, может полностью или частично нейтрализоваться, чтобы отразить конфликтующие области влияния.
Наконец, карты влияния легко визуализировать при отрисовке в мире. Они могут стать ценной подсказкой дизайнерам, которым нужно настраивать ИИ на основании видимых свойств, и за ними можно наблюдать в реальном времени, чтобы понять, почему ИИ выбирает принимаемые им решения.
Надеюсь, статья дала вам общую картину самых популярных инструментов и подходов, используемых в игровом ИИ, а также ситуаций, в которых они могут применяться. В статье не рассмотрено множество других техник (они используются реже, но потенциально могут быть столь же эффективными), в том числе и следующие:
- алгоритмы задач оптимизации, в том числе поиск восхождением к вершине, градиентный спуск и генетические алгоритмы.
- состязательные алгоритмы поиска/планирования, такие как минимакс и альфа-бета-отсечение
- техники классификации, например, перцептроны, нейронные сети и метод опорных векторов
- системы обработки восприятия и памяти агентов
- архитектурные подходы к ИИ, такие как гибридные системы, предикативные архитектуры (архитектуры Брукса) и другие способы разложения систем ИИ на слои
- инструменты анимации, такие как планирование движения (motion planning) и motion matching
- задачи обеспечения производительности, такие как уровни детализации (level of detail), алгоритмы с отсечением по времени (anytime algorithms) и квантование времени (timeslicing)
Чтобы прочитать подробнее об этих темах, а также о темах, рассмотренных в статье, можно изучить следующие источники.
Многие из самых качественных материалов можно найти в книгах, в том числе и в следующих:
- Серия The Game AI Pro — это сборник коротких статей, объясняющих реализацию конкретных функций или решению конкретных проблем. На http://www.gameaipro.com/ выложены бесплатные фрагменты из предыдущих книг.
- Серия AI Game Programming Wisdom была предшественницей серии Game AI Pro. В ней содержатся слегка устаревшие техники, но почти все они актуальны и сегодня. Эти книги встречаются редко, так что ищите их в цифровых копиях или на распродажах!
- Artificial Intelligence: A Modern Approach — один из стандартных текстов для тех, кто хочет разобраться в общей тематике искусственного интеллекта. Эта книга не относится конкретно к играм, и иногда может быть сложной, но она даёт непревзойдённый обзор области и учит основам, на которых построены многие игровые ИИ.
Кроме того, есть несколько хороших книг об игровом ИИ в целом, написанных профессионалами этой отрасли. Сложно отдать предпочтение какой-то одной — прочитайте обзоры и выберите ту, которая подходит вам.
Комментариев нет:
Отправить комментарий