Самая простая реализация ограничения — это принудительная установка в некоторое значение при превышении определённого уровня. Например, для синусоиды с возрастающей амплитудой это будет выглядеть так:

В роли ограничителя здесь выступает функция Clip, в качестве аргумента которой передаётся входной сигнал и параметры ограничения, а результатом функции является выходной сигнал.
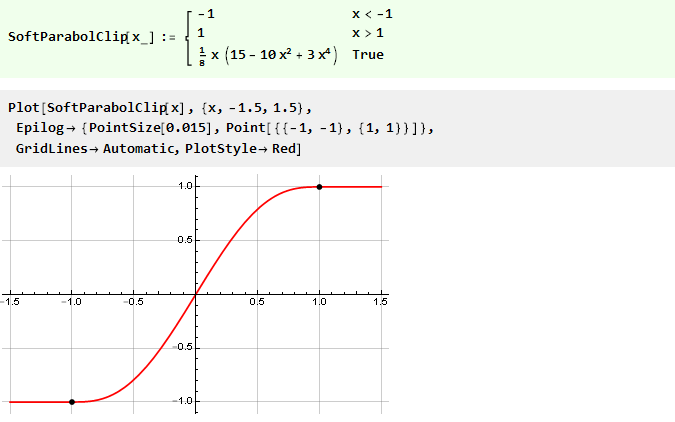
Посмотрим на график функции Clip отдельно:
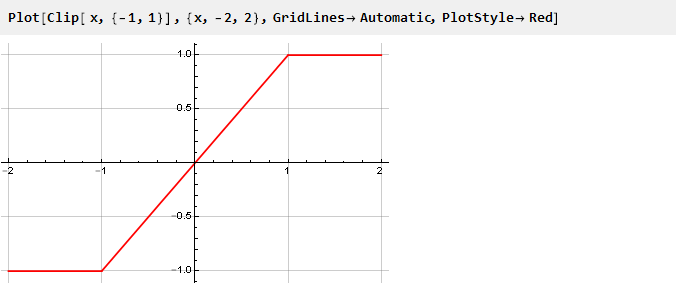
Из него видно, что пока мы не превышаем пределы ограничения, выходное значение равно входному и сигнал не меняется; при превышении же выходное значение от входного уже никак не зависит и остаётся на одном и том же уровне. По сути, мы имеем кусочно-непрерывную функцию, составленную из трёх других: y=-1, y=x и y=1, выбираемых в зависимости от аргумента, и эквивалентную следующей записи:

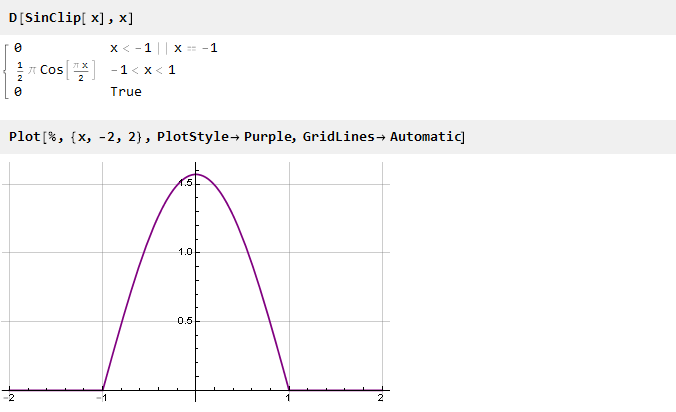
Переход между функциями происходит довольно резко; и выглядит заманчивым сделать его более плавным. Математически эта резкость обусловлена тем, что производные функций в точках стыковки не совпадают. Это легко увидеть, построив график производной функции Clip:
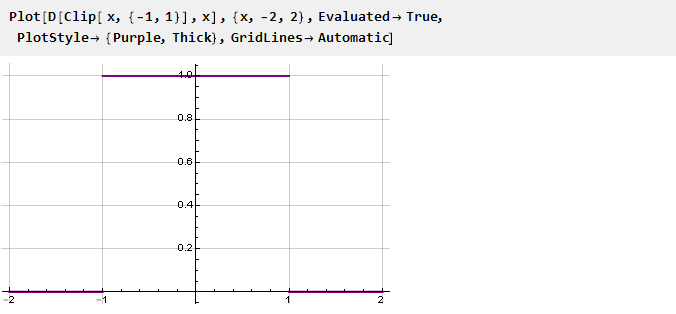
Таким образом, чтобы обеспечить гладкость функции ограничения, необходимо обеспечить равенство производных в точках стыковки. А поскольку крайние функции у нас константы, производные от которых равны нулю, то и производные функции ограничения в точках стыковки тоже должны быть равны нулю. Далее будут рассмотрены несколько таких функций, обеспечивающих гладкую стыковку.
Синус
Самое простое — это использовать функцию sin на интервале от -pi/2 до pi/2, на границах которого значения производной равны нулю по определению:
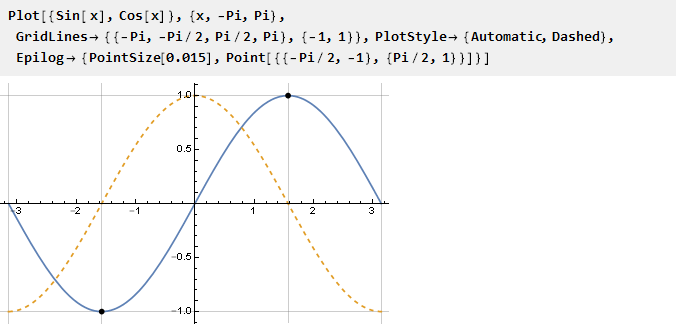
Нужно только масштабировать аргументы, чтобы единица проецировалась на Pi/2. Теперь мы можем определить собственно ограничивающую функцию:

И построить её график:
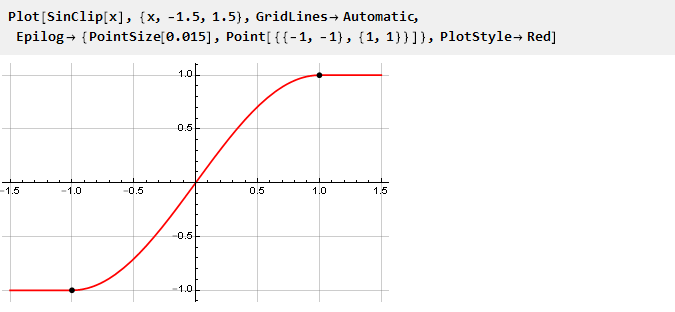
Так как пределы ограничения у нас жёстко определены, то ограничение задаётся через масштабирование входного сигнала с последующим (при необходимости) обратном масштабировании.
Здесь также уже нет ситуации, при которой входной сигнал передаётся на выход без искажений — чем меньше уровень усиления, тем меньше уровень искажений вследствие ограничения — но сигнал искажается в любом случае.
Влияние параметра усиления на искажение сигнала можно посмотреть и в динамике:

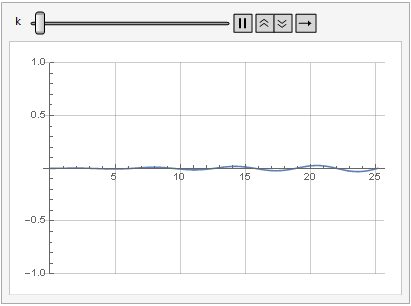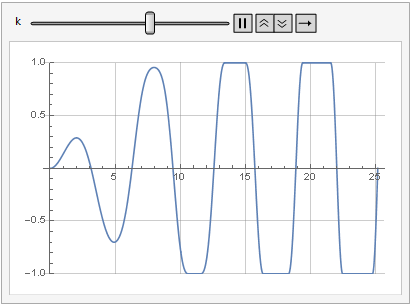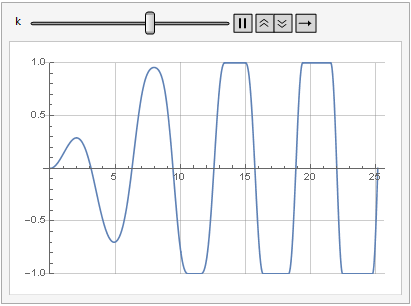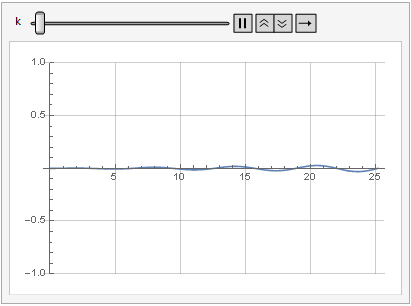
Больше гладкости
Посмотрим на производную нашей функции:
В ней уже нет разрывов в значениях, но есть разрывы в производной (второй, если считать от изначальной функции). Для того, чтобы её устранить, можно пойти обратным путём — сначала сформировать гладкую производную, а затем её проинтегрировать для получения искомой функции.
Самый простой способ обнулить производную точках -1 и 1 — это просто возвести функцию в квадрат — все отрицательные значения функции станут положительными и, соответственно, возникнут перегибы в точках пересечения функции с нулём.
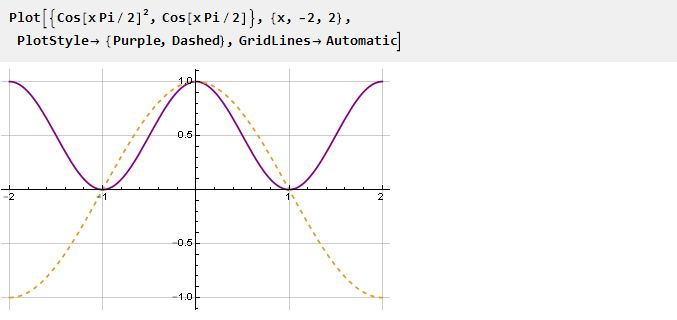
Находим первообразную:
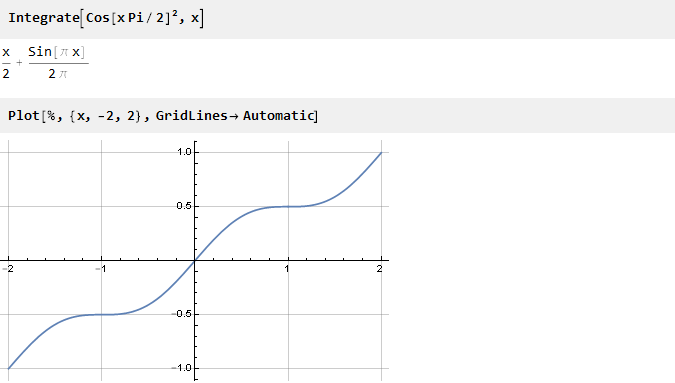
Теперь осталось масштабировать её по оси ординат. Для этого найдём её значение в точке 1:

И поделим на неё (да, конкретно здесь это элементарное умножение на 2, но далеко не всегда так бывает):

Таким образом, итоговая функция ограничения примет вид:
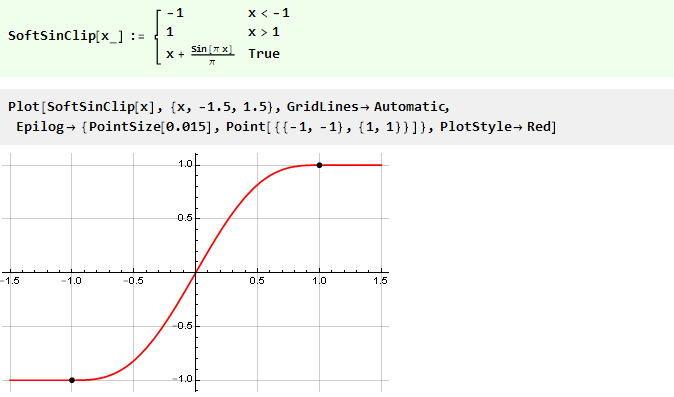
Переходим на полиномы
Использование тригонометрический функций в некоторых случаях может оказаться несколько расточительным. Поэтому попробуем построить необходимую нам функцию, оставаясь в рамках элементарных математических операций.
Рассмотрим параболу:
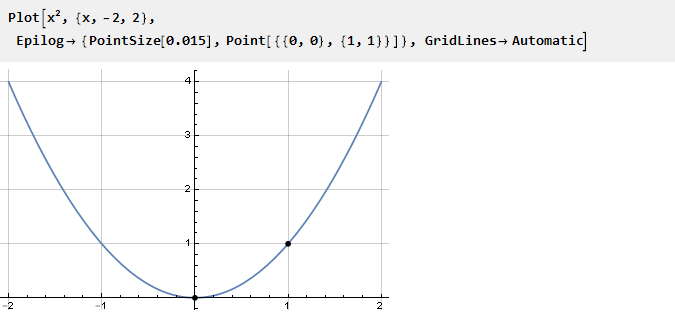
Так как у неё уже есть перегиб в точке ноль, мы можем использовать одну и ту же часть на интервале {0,1} для для стыковки с константами. Для отрицательных значений её нужно сместить вниз и влево:

а для положительных — отразить по вертикали и горизонтали:

И наша функция с параболой примет вид:
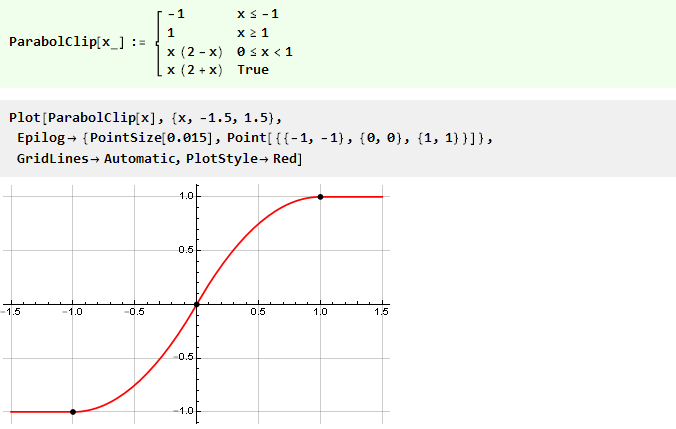
Немного усложним
Вернёмся к нашей параболе, перевернём её и сместим на единицу вверх:
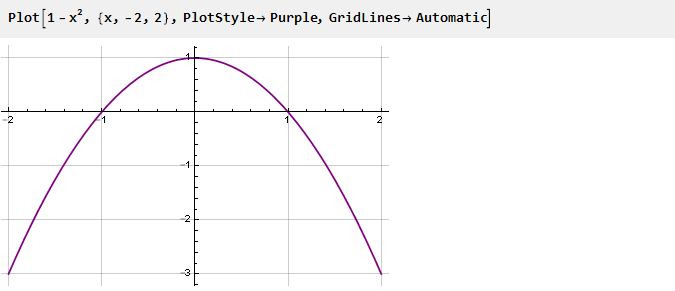
Это будет производная нашей функции. Чтобы сделать её более гладкой в точках стыковки, возведём в квадрат, обнулив таким образом вторую производную:
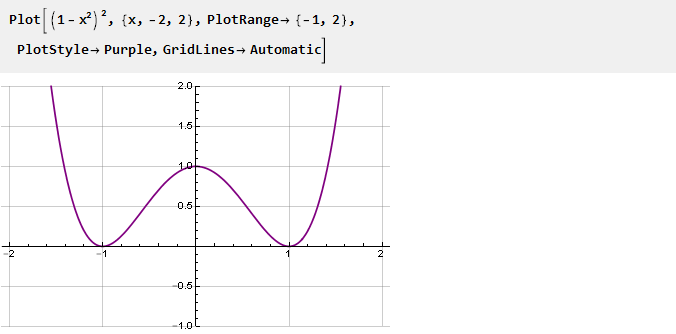
Интегрируем и масштабируем:

Получаем ещё более гладкую функцию:
Больше гладкости богу гладкости
Здесь мы попробуем добиться гладкости в точках стыковки на ещё более высших производных. Для этого для начала определим функцию как полином с неизвестными коэффициентами, а сами коэффициенты попробуем найти через решение системы уравнений.
Начнём со 1-й производной:

2-я:

3-я:

Все эти коэффициенты выглядит так, как будто в них есть какая-то логика. Выпишем множители, помножив их на значение степени при х; а чтобы не писать каждый раз одно и тоже, автоматизируем процесс нахождения коэффициентов:

Похоже на биномиальные коэффициенты. Сделаем смелое предположение, что это они и есть, и исходя из этого, запишем обобщённую формулу:

Проверим:
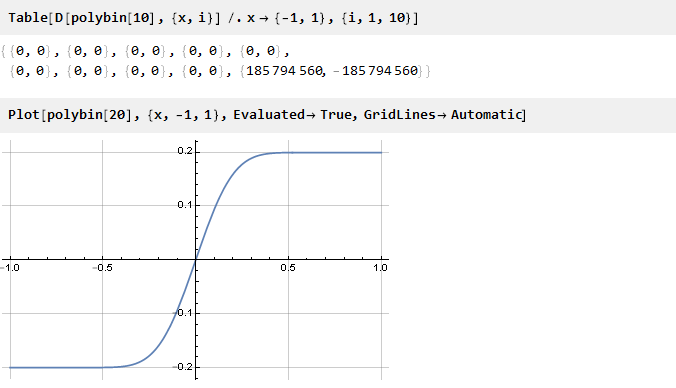
Похоже на правду [1]. Осталось только посчитать масштабный коэффициент, чтобы привести края к единице:

А после масштабирования и упрощения мы обнаружим, что наши познания в математике несколько устарели [2]:
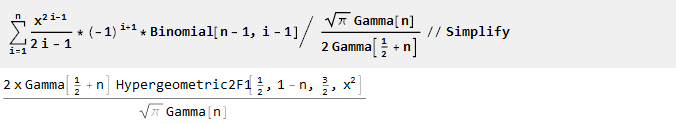
Таким образом, мы получили производящую функцию порядка n, в которой n-1 первых производных будут равны нулю:

Посмотрим, что получилось:
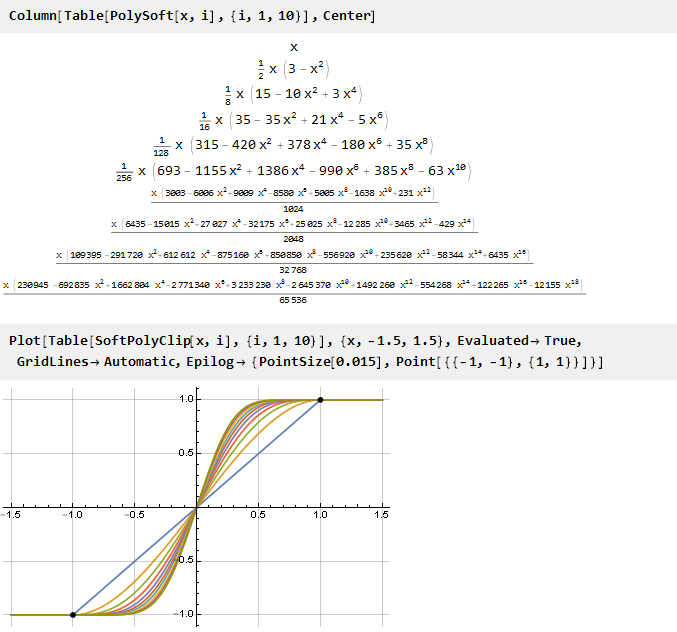
И поскольку наша обобщённая формула получилась непрерывной, при желании можно использовать и нецелые значения параметров:
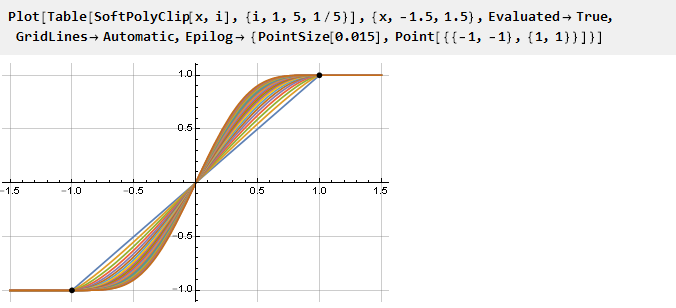
Также можно построить графики производных, приведённых к одному масштабу:
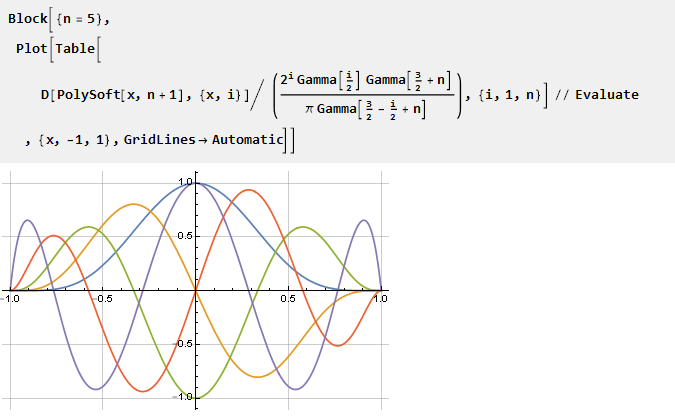
Добавляем жёсткости
Было бы заманчиво, иметь возможность регулировать и степень «жёсткости» ограничения.
Вернёмся к нашей перевёрнутой параболе и добавим коэффициент при степени x:

Чем больше n, тем больше наша производная «квадратная», а её первообразная — соответственно, резкая:
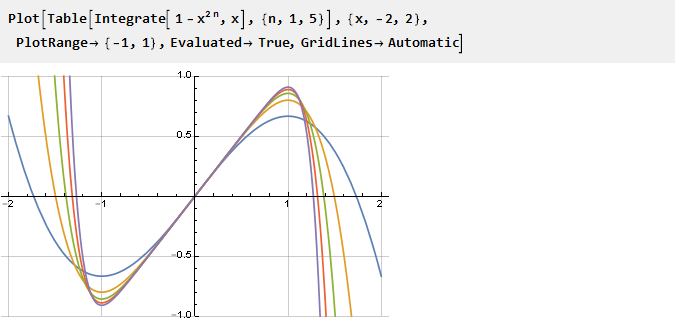
Посчитаем первообразную и скорректируем масштаб:

Попробуем теперь задать дробный шаг для параметра:
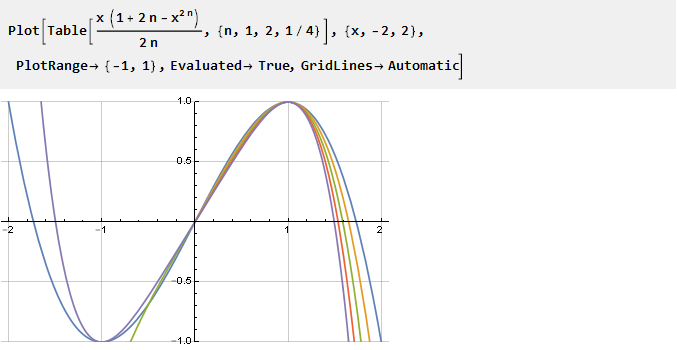
Как видим, в отрицательной части не для всех n имеется корректное решение, но в правой (положительной) части необходимые нам условия по-прежнему соблюдаются — поэтому для отрицательных значений мы можем просто использовать её в перевёрнутом виде с реверсированным аргументом. И поскольку область определения параметра уже не ограничена только положительными целыми числами, то можно упростить формулу, заменив 2n на n:

А заменив n на n-1, можно сделать формулу чуть более красивой:
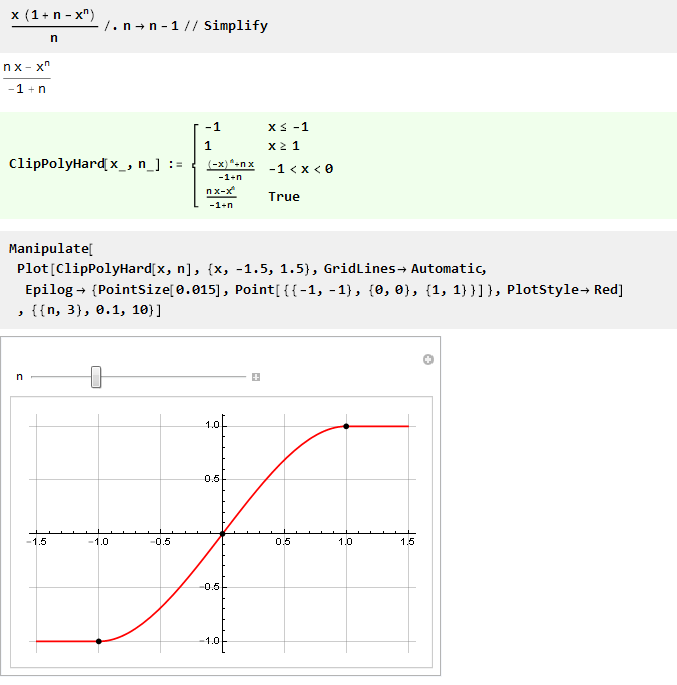
Поскольку при n равным единице мы получаем деление на ноль, то попробуем найти предел:

Предел находится, а значит, теперь можно доопределить [3] функцию для n равным 1 и рассматривать её для всех n больших нуля:
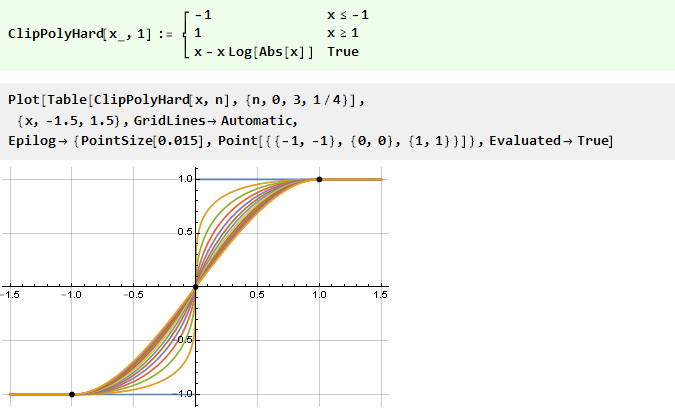
Если же мы изначально возведём нашу перевёрнутую параболу в квадрат, то получим ещё более гладкую функцию:
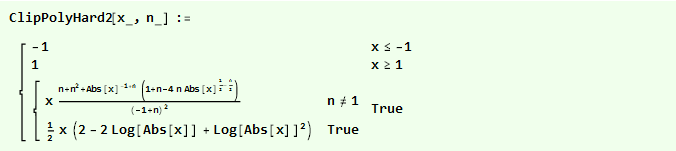
И можем сравнить их на одном графике:
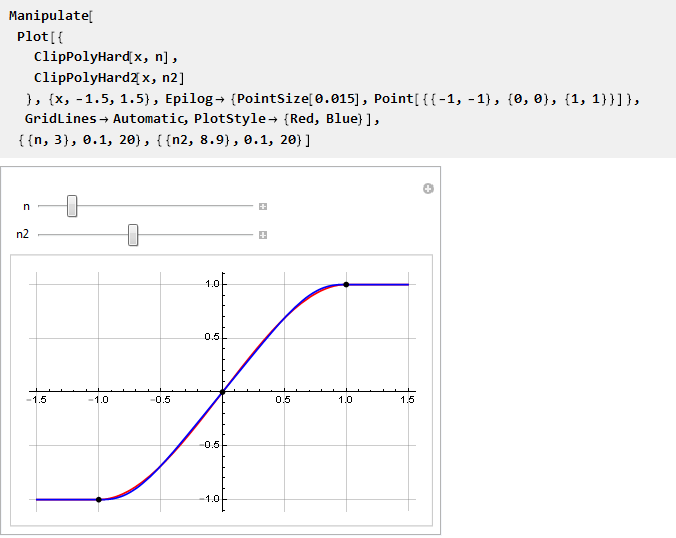
Рационализируй это
Посмотрим на следующую функцию:
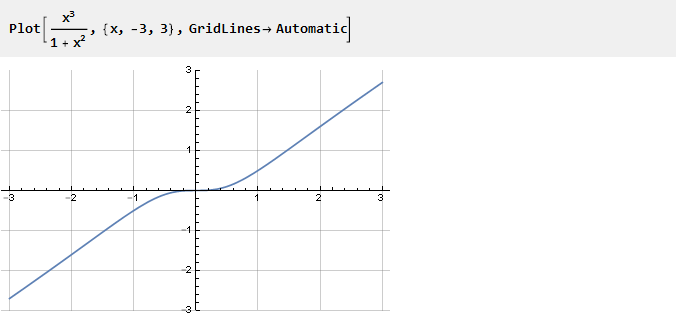
Появилась она не случайно.
Если убрать из неё единицу, x2 сократится и останется просто x, т.е наклонная прямая. Таким образом, чем меньше значение x, тем большее влияние оказывает единица в знаменателе, создавая необходимое нам искривление. А рассматривая эту функцию в разных масштабах, можно контролировать степень этого искривления:

Таким образом, мы можем переписать предыдущую функцию с контролем жёсткости, используя только рациональный полином 3-порядка:
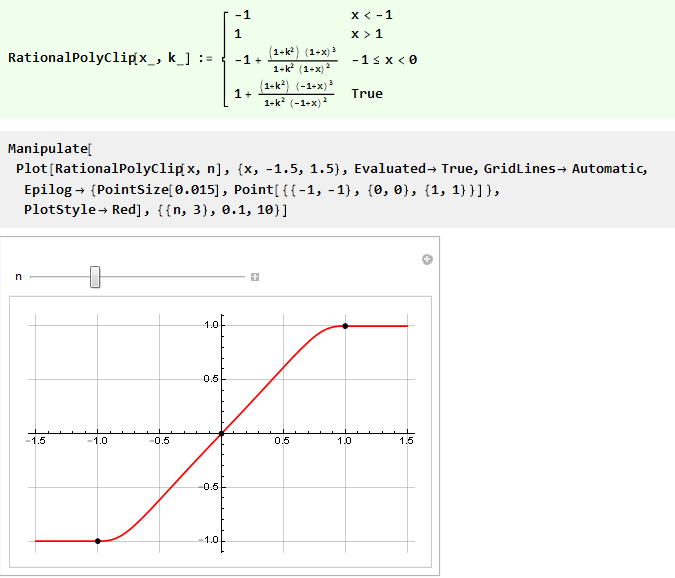
Автоматизируй это
Чтобы не задавать каждый раз кусочно-непрерывные функции, мы можем определить вспомогательную функцию, которая сделает это самостоятельно, принимая на вход донорскую функцию в качестве аргумента.
Если наша функция уже обладает диагональной симметрией и выровнена по центру координат (как синусоида), то можно сделать просто
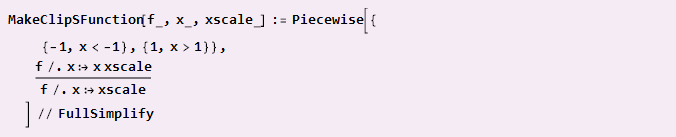
Пример использования:

Если же нужно собирать из кусочков, как в случае с параболой, и центр координат определяет точки стыковки, то формула слегка усложнится:
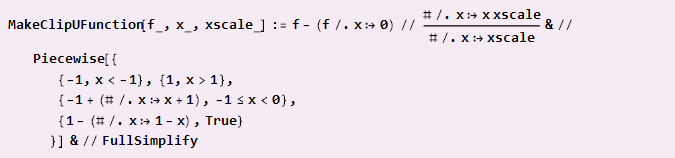
Пример использования:

Перейдём на экспоненту
Совершенно любая функция может быть донором для решения этой задачи, нужно лишь только обеспечить ей точки перегиба. Возьмём, например, сдвинутую вниз на единицу экспоненту:
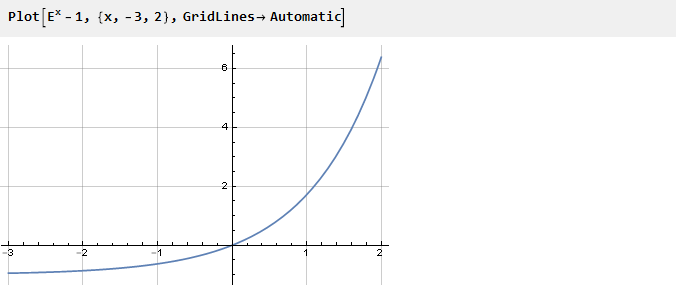
Ранее, для обеспечения необходимого перегиба в точке ноль, мы возводили функцию в квадрат. Но можно пойти и другим путём — например, суммировать с другой функцией, производная которой в точке ноль противоположна по знаку с производной экспоненты. Например, -x:
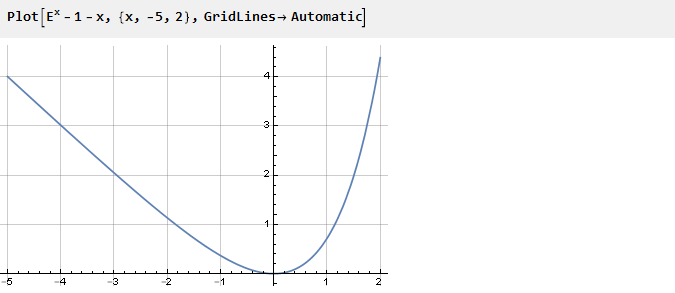
В зависимости от того, с какой стороны мы будем брать кривую, будет и зависеть итоговый вид функции. Теперь, воспользовавшись ранее определённой вспомогательной функцией и выбрав одну из сторон, получим:

Либо

И теперь можем сравнить их на одном графике:
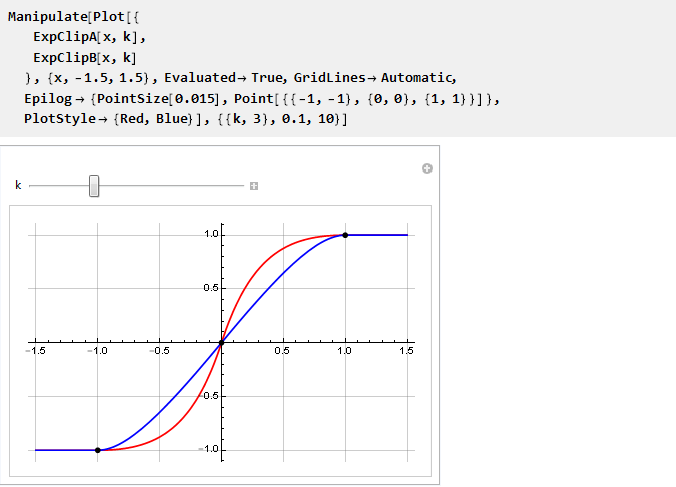
Видно, что при k→0 они стремятся к совпадению; и так как напрямую посчитать их значения мы не можем, поскольку получим деление на ноль, то воспользуемся пределом:

И получили уже известную нам кусочную функцию из параболы.
Нарушая симметрию
Пока что мы рассматривали исключительно симметричные функции. Однако бывают случаи, когда симметрия нам не нужна — например, для имитации искажений при звучании ламповых усилителей.
Возьмём экспоненту и умножим её на перевёрнутую параболу в квадрате — чтобы получить пересечение с осью абсцисс в точках -1 и 1, а заодно и обеспечить гладкость второй производной; параметризацию же осуществим через масштабирование аргумента экспоненты:
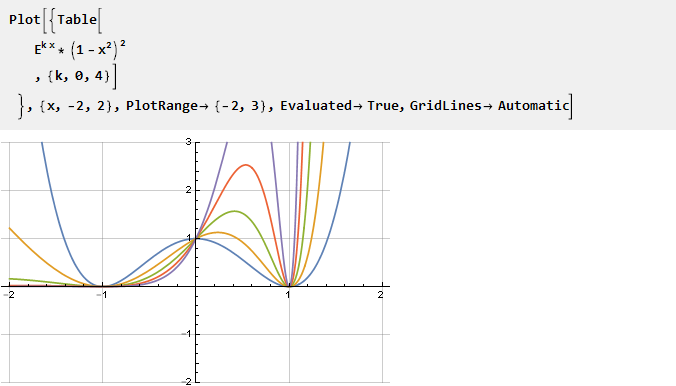
Найдём первообразную и масштабируем её:
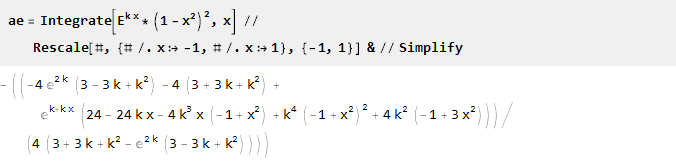
Так как при k=0 получим деление на ноль:

То дополнительно найдём предел,

который представляет из себя уже известный нам гладкий полином 3-го порядка. Соединив всё в одну функцию, получим
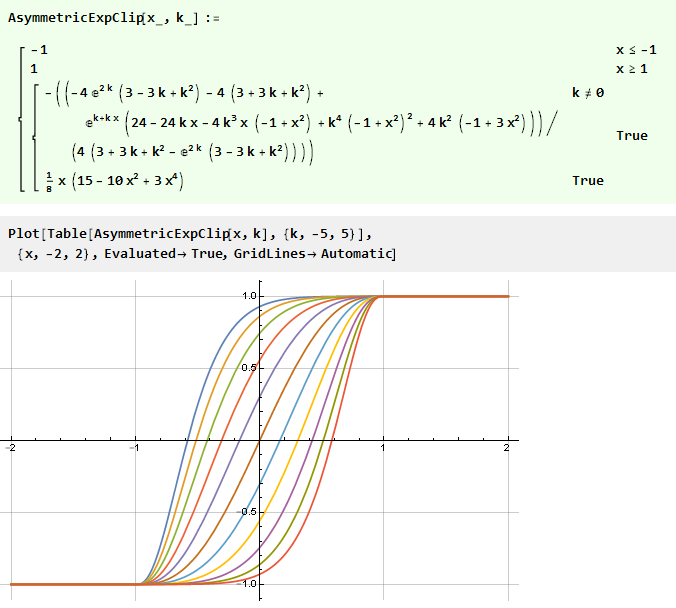
Вместо того, чтобы изначально проектировать асимметричную функцию, можно пойти и другим путём — использовать готовую симметричную, но «искривлять» значение этой функции с помощью дополнительной функции кривой, определённой на промежутке {-1,1}.
Рассмотрим, например, гиперболу:
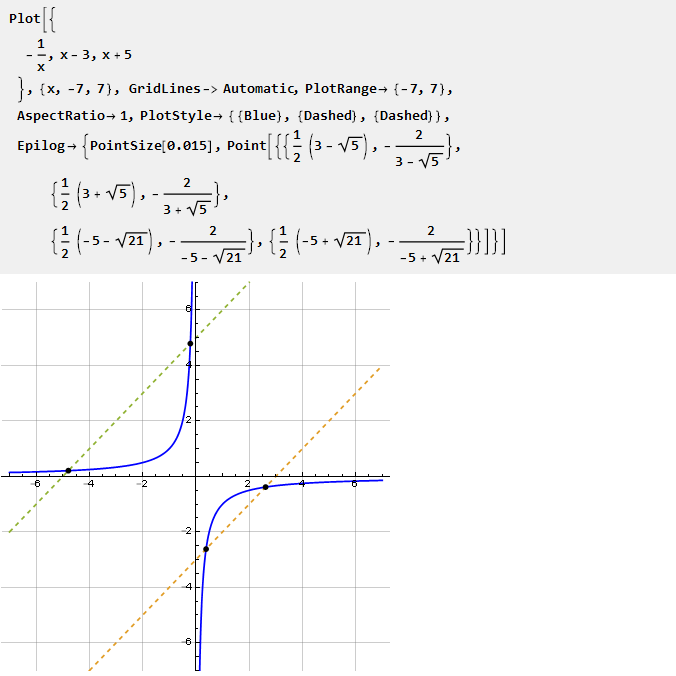
Рассматривая её отрезок в разных масштабах, можно регулировать степень искривления в обе стороны. Как же найти этот отрезок? Исходя из графика, можно было бы искать пересечения гиперболы с прямой. Однако, поскольку такое пересечение существует не всегда, это создаёт некоторые сложности. Поэтому мы пойдём другим путём.
Для начала добавим в гиперболу масштабирующие коэффициенты:

затем составим систему уравнений, задающих условия прохождения гиперболы через заданные точки — и её решение даст интересующие нас коэффициенты:

Теперь подставим решение в исходную формулу и упростим:

Посмотрим, что у нас получилось в зависимости от параметра k:
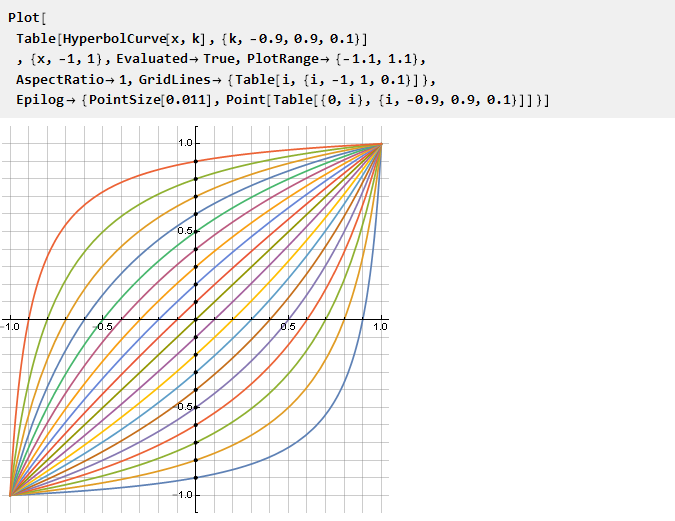
Примечательно, что при k=0 формула естественным образом схлопывается в x и никаких особых ситуаций не происходит — хотя применительно к исходной гиперболе это равносильно отрезку нулевой длины, причём двум сразу. Не менее примечательно, что обратной к ней функцией является она же самая, но с отрицательным параметром k:

Теперь мы можем использовать её для модификации произвольной функции ограничения, а параметр k таким образом будет задавать точку пересечения с осью ординат:
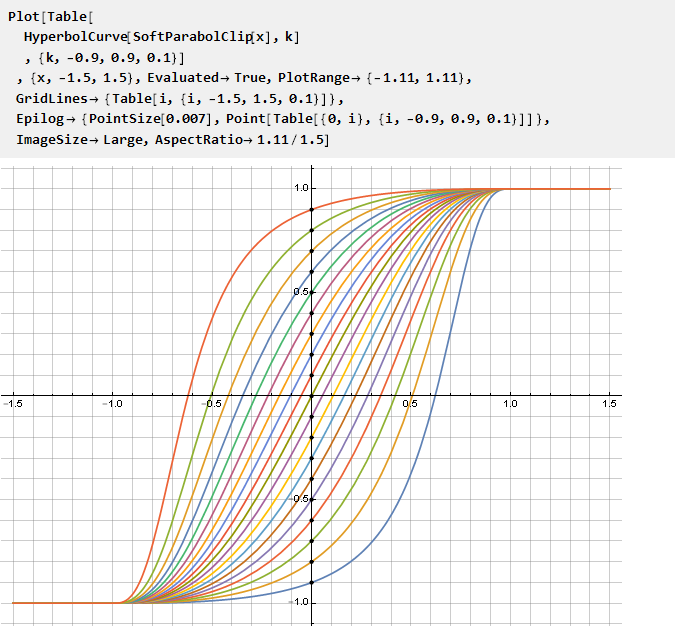
Аналогичным образом можно строить кривые и из других функций, например, степенной с переменным основанием:
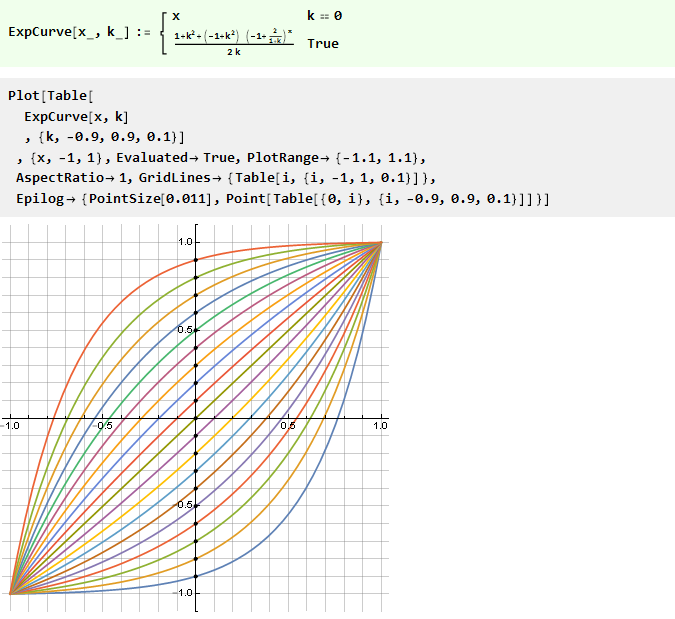
Или обратной к ней логарифмической:
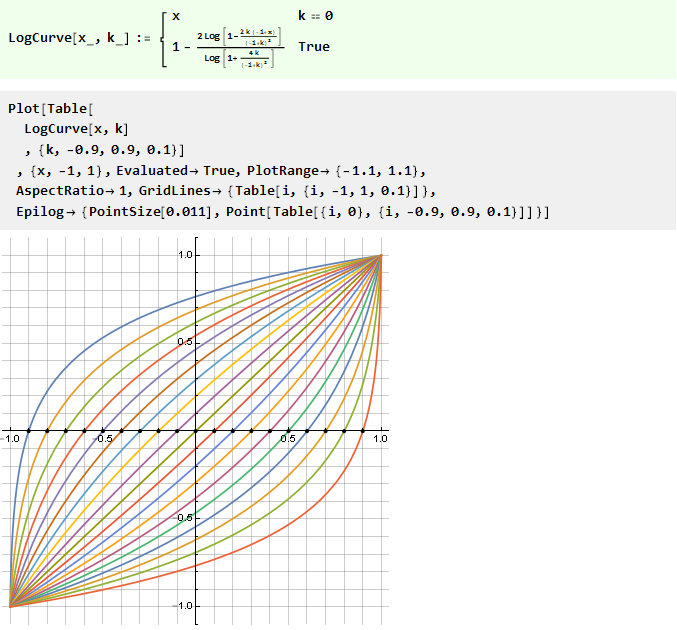
Нужно больше точности
Мы можем захотеть иметь гарантированно линейный промежуток у функции на некотором интервале. Это логично организовать введением прямой линии в кусочно-непрерывную функцию,
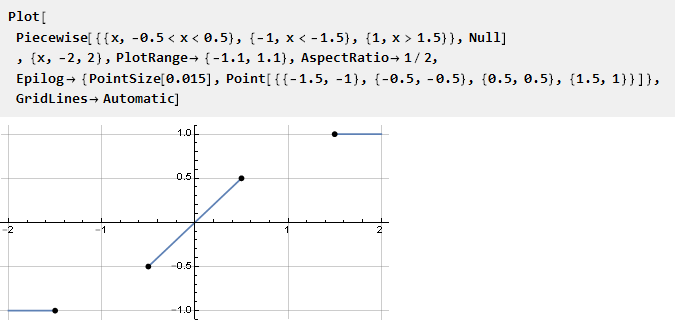
пустые места в которой необходимо заполнить какой-нибудь функцией. Очевидно, что для гладкой стыковки с линейным участком её первая производная должна быть равна единице; а все последующие (по возможности) нулю. Чтобы не не выводить такую функцию заново, мы можем взять уже готовую и адаптировать под эту задачу. Также можно заметить, что крайние точки отстоят чуть дальше единицы — это необходимо, чтобы сохранить наклон линейного участка.
Возьмём выведенную ранее функцию PolySoft и сместим её так, чтобы в центре координат получить единицу:
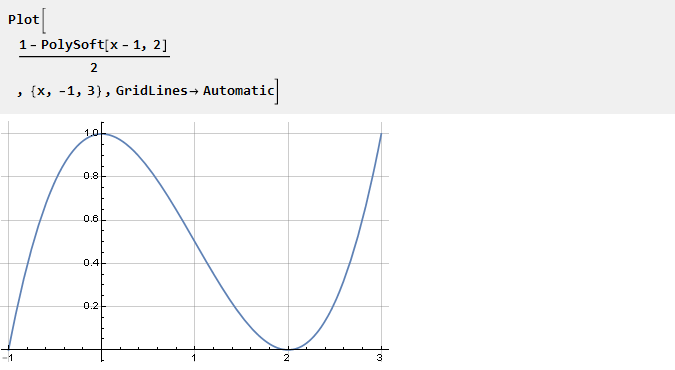
Из её свойств следует, что n-1 последующих производных в точках 0 и 2 будут равны нулю:
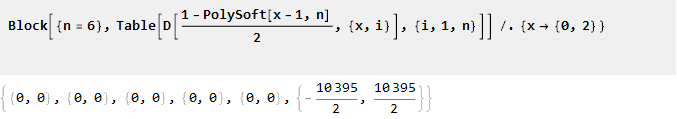
Теперь проинтегрируем её:
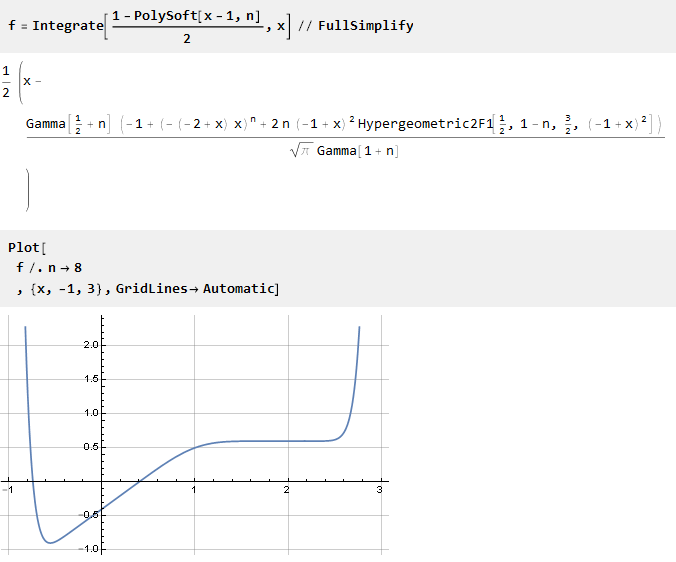
Функция оказалась сдвинутой вниз относительно оси абсцисс. Поэтому необходимо добавить константу (равную значению функции в точке 0), чтобы совместить центры координат:

Здесь у нас появился ноль в степени n. Он не сократился, так как значение ноль в степени ноль не определено; мы можем его удалить вручную, а можем при упрощении явно указать, что n у нас больше нуля:

Проверим на всякий случай. Значение в точках 0 и 2 для всех n:

Производные на краях интервала (для полинома порядка 5):

Как видим функция получилась довольно громоздкой. Чтобы не таскать её и не переусложнять вычисления, дальше будем манипулировать уже с конкретным полиномом, например 4-го порядка:

И вот теперь ею можно заполнить свободное пространство:

Проверим:
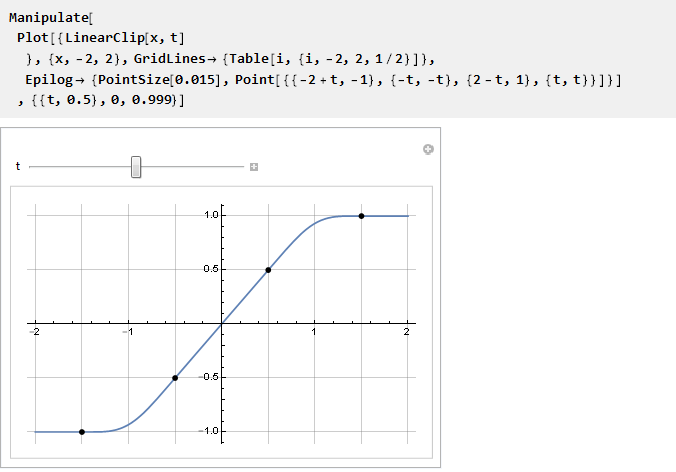
Уходим в бесконечность
Иногда может оказаться потребность в функциях, которые стремятся к единице, но не достигают её. Википедия подсказывает несколько известных решений:
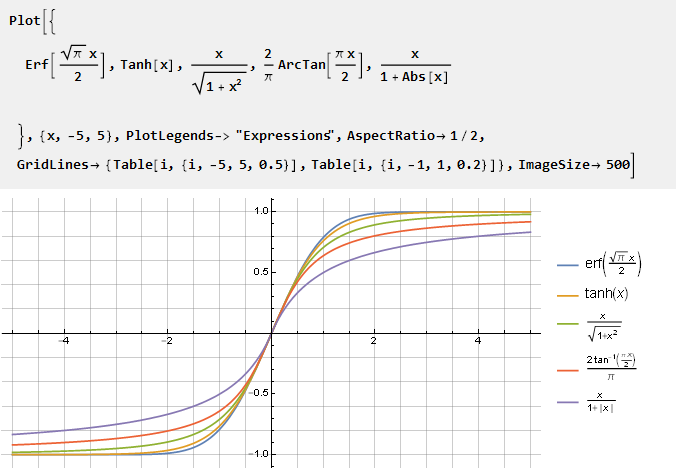
Так как эти функции единицы не достигают, их удобнее нормировать по производной в центре координат.
Мы можем модифицировать форму таких функции через их аргумент с помощью какой-нибудь диагонально-симметричной функции, например:
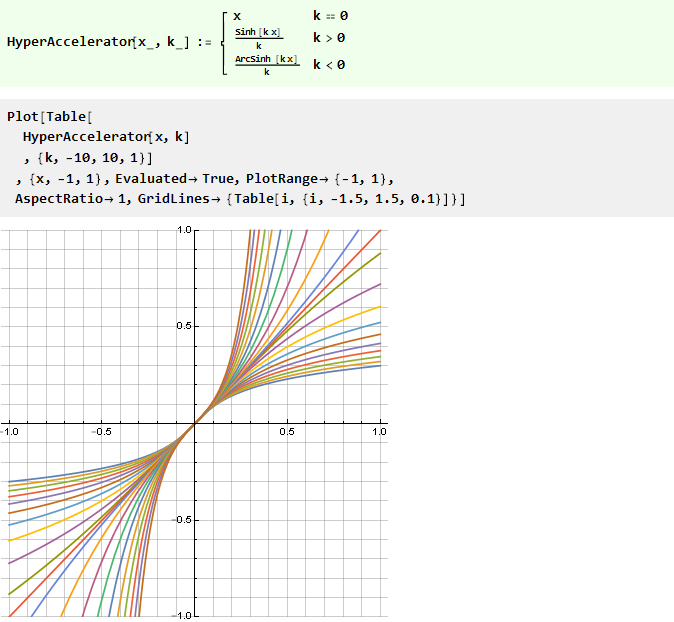
Эта функция, к слову, также является обратной самой к себе, т.е.
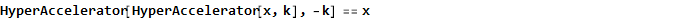
И, применительно к арктангенсу в качестве примера, получим
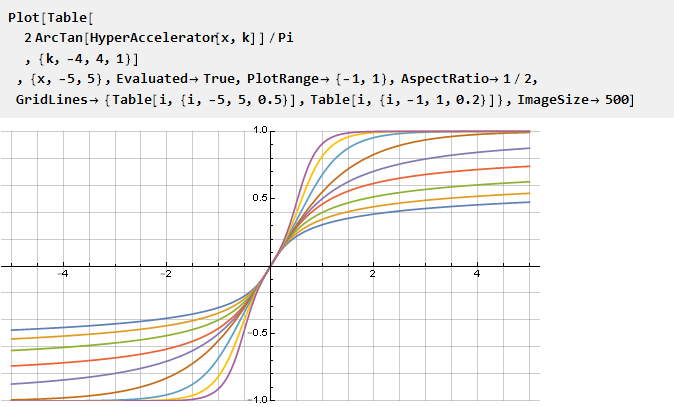
что, в частности, с параметром k=1 даст нам функцию Гудермана.
Как видим, при таком подходе можно получить нежелательные перегибы, поэтому более предпочтительно контролировать жёсткость ограничения непосредственно через свойство самой функции. Рассмотрим несколько таких функций с параметром, вывод которых для краткости опустим.
Из степенной функции:
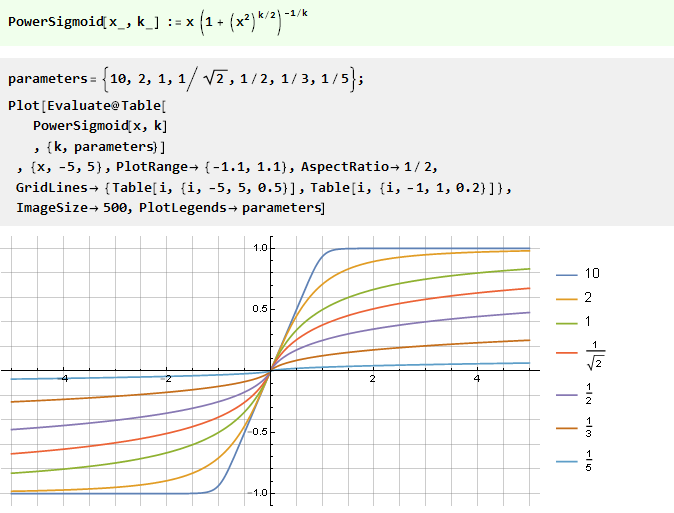
Из суммы двух v-образных функций со смещением:
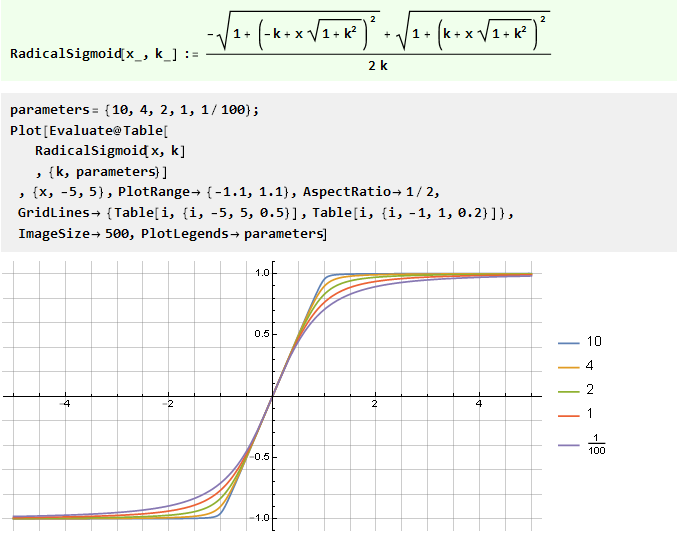
Из обобщённой функции ошибок:
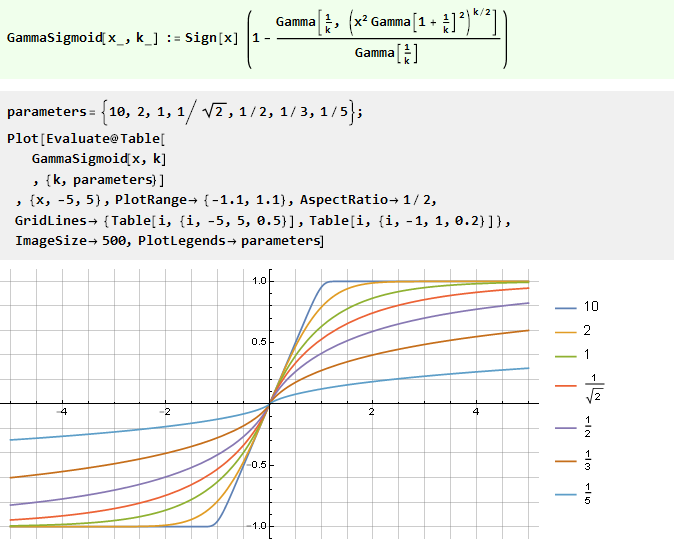
Интегрированием рационального полинома:
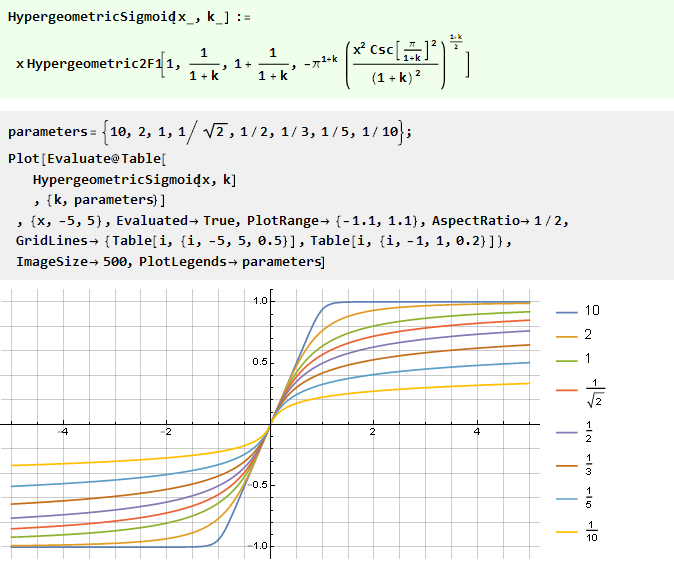
Интересно, что её частным случаем является арктангенс:

Заключение
Построение подобного рода функций может быть увлекательным занятием, в ходе которого будут получаться как простые, так и сложные, как красивые, так и не очень, формулы. Может показаться, что все они сильно друг на друга похожи и надобности в подобном разнообразии нет. Это не обязательно так.
Разница может быть сильнее видна в других масштабах — например, логарифмическом. Кроме того, помимо обозначенных в заголовке задач, подобные функции могут использоваться и в других задачах — смешивании сигналов, когда плавное затухание одного сигнала сочетается с плавным нарастанием другого, или построении акустических фильтров — и тогда разница будет восприниматься на слух, или же для построения градиентов — и тогда разница будет восприниматься на глаз. Кроме того, они также могут использоваться в качестве доноров для других, более сложных функций — например, оконных.
В завершение стоит уточнить ещё несколько моментов.
Все функции здесь были определены в диапазоне от -1 до 1. В случае, если нужен другой диапазон (например, от 0 до 1), его легко можно пересчитать либо вручную:
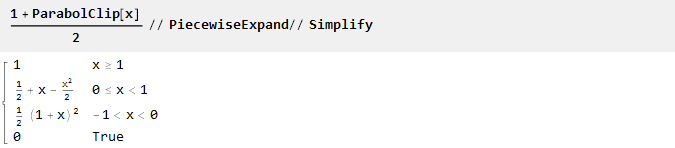
Либо используя встроенную функцию масштабирования:

А для облегчения экспорта полученных формул в программный код может пригодиться функция CForm:
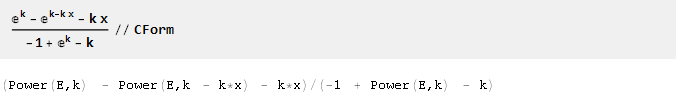
Исходный документ Mathematica можно скачать здесь.
Примечания:
[1] настоящий математик наверняка сможет строго доказать (или опровергнуть) это утверждение.
[2] в стандартном курсе мат.анализа гипергеометрические функции не рассматриваются.
[3] эта перегрузка определена только для символьной единицы; единица в формате с плавающей точкой (например, при построении графика) распознана не будет.
Комментариев нет:
Отправить комментарий