В марте 2016 года Роберт Дж. Лемке-Оливер и Каннан Соундарараджан из Стэнфордского университета открыли новый шаблон в распределении простых чисел. Оказалось, что простые числа специфически распределяются по числовому пространству. Подробнее см. перевод статьи «Структура и случайность простых чисел» на Хабре.
К изучению темы подключились специалисты из других областей, в том числе химии. И успешно. Профессор теоретической химии Сальваторе Торкуато вместе с теоретиком чисел Мэтью де Курси-Айрлэнд нашли новые шаблоны в распределении простых чисел, о которых раньше не было известно. Оказалось, что распределение простых чисел образует фракталоподобную дифракционную картину, чем-то похожую на картину дифракции у экзотических квазикристаллов.
Профессор Торкуато специализируется на изучении закономерностей в структурах физических систем, таких как кристаллы и коллоиды. Стандартный способ изучения структуры — дифракция рентгеновских лучей. Беспорядочные молекулы в жидкостях или газе отражают лучи во всех направлениях, не создавая заметного рисунка. Но симметрично расположенные атомы в кристалле синхронно отражают световые волны, создавая периодические яркие пятна выраженной дифракции (пики Брэгга). Анализ пиков Брэгга даёт возможность понять внутреннюю структуру кристалла или иного материала, который создаёт такую картину.
Так вот, в новых научных статьях Торкуато и других (1, 2, 3) показано, что обнаруженная упорядоченная структура в распределении простых чисел — ни что иное как фракталоподобная дифракционная картина, примерно как у квазикристаллов.
Картина пиков Брэгга на решётке из простых чисел похожа на квазикристаллы, но всё-таки отличается от них. Торкуато говорит, что простые числа как физическая система «являются совершенно новой категорией структур». Исследователи назвали этот новый фракталоподобный рисунок «эффективной предельной периодичностью» (effective limit-periodicity).
Рисунок состоит из периодической последовательности светлых вершин, которые отражают наиболее общие интервалы простых чисел: все они нечётные (кроме 2), многие рядом друг с другом. Самые яркие пики (пары, разделённые двумя цифрами) чередуются через равные промежутки времени с менее яркими пиками, отражая простые числа, разделённые шестью цифрами. Между ними ещё более тусклые пики, соответствующие более удаленным парам простых чисел и т. д. Всё это — бесконечное количество пиков Брэгга, помещённых друг внутрь друга.
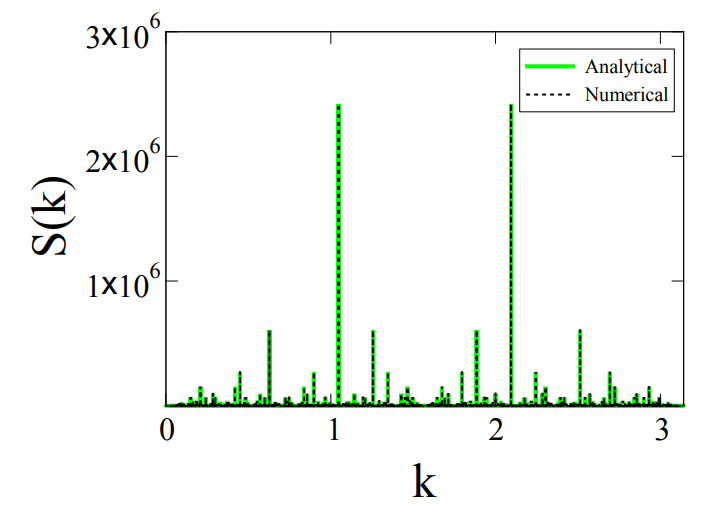
Подобная структура пиков Брэгга наблюдалась и раньше — в дифракционных картинах квазикристаллов.
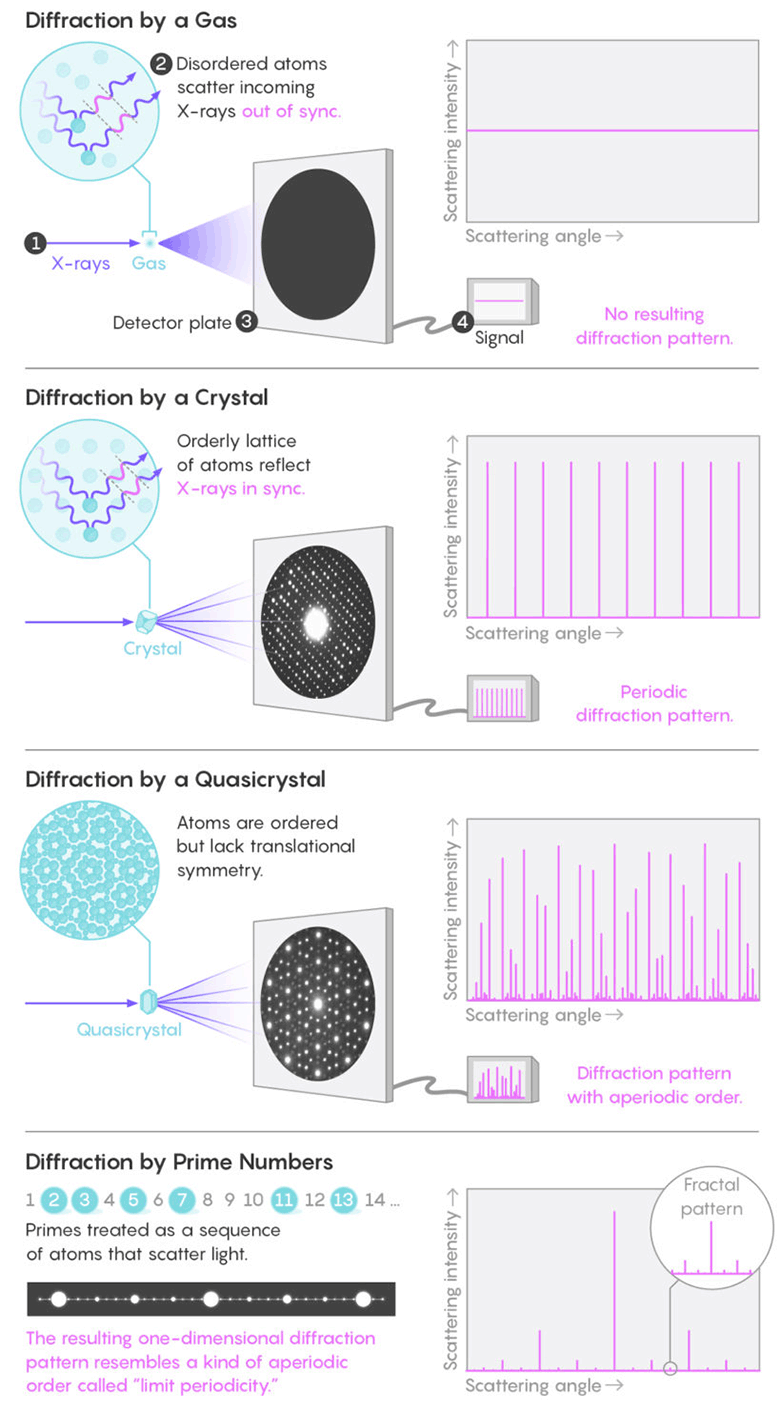
Беспорядочные молекулы в жидкостях или газе отражают лучи во всех направлениях, не создавая заметного рисунка. Но симметрично расположенные атомы в кристалле синхронно отражают световые волны, создавая периодические яркие пятна выраженной дифракции. Как выяснилось, шаблон распределения простых чисел образует фрактальную дифракционную картину, примерно как у квазикристаллов
Квазикристаллы — странные материалы, обнаруженных в 1980-х годах. Они характеризуются симметрией, запрещённой в классической кристаллографии, и наличием дальнего порядка. Математической моделью квазикристаллов являются апериодичные мозаики типа известной мозаики Пенроуза. В таких мозаиках отсутствует трансляционная симметрия, присутствует повторяемость и квазикристалличность (симметрия пятого порядка).
Фрагмент мозаики Пенроуза типа P1 (из плиток шести типов)
В случае простых чисел расстояния между пиками являются пропорциональными частями друг друга, в отличие от иррационально разнесённых пиков Брэгга квазикристаллов. «Простые числа фактически предполагают совершенно другое состояние позиций частиц, похожее на квазикристаллы, но не похожее на квазикристаллы», — сказал Торкуато.
Открытие дифракционной картины нельзя назвать прорывным открытием для теории чисел, потому что основная часть этих шаблонов уже была описана ранее, только другими математическими методами (не через дифракцию квазикристаллов). Так, с помощью дифракционной картины возможно предсказание «двойников» типа 17 и 19 — это математический эквивалент первой гипотезы Харди — Литлвуда относительно существования кортежей простых чисел на данном отрезке числовой прямой. Одно из правил запрещает триплеты из последовательных нечётных чисел после {3, 5, 7}. Это же объясняет, почему следующий по яркости пик Брэгга в дифракционной картине соответствует числам, разделённым шестью цифрами, а не четырьмя.
Новая научная работа — просто свежий взгляд на проблему равномерного распределения простых чисел и более простой способ вывести некий «единый закон» для них. Кроме того, это необычный способ анализа математической проблемы с точки зрения кристаллографии, а именно с точки зрения относительно молодой области исследований, называемой «апериодическим порядком», которая изучает неповторяющиеся модели и лежит на пересечении кристаллографии, динамических систем, гармонического анализа и дискретной геометрии. Эта отрасль науки выросла после открытия квазикристаллов, когда стало понятно, что старые методы тут не работают.
Распределение простых чисел напоминает особый апериодический порядок, известный с 1950-х годов. Он называется предельной периодичностью (limit periodicity). В таких системах периодические интервалы вложены в бесконечную иерархию, так что в любом интервале система содержит части шаблонов, которые повторяются только в большем интервале, как в плитке Тейлора-Соколара.

Плитка Тейлора-Соколара
Теоретические расчёты показывают, что предельно-периодические фазы вещества должны иметь возможность формироваться в природе, и такие системы могут иметь необычные свойства. Но никто не догадался связать предельную периодичность с простыми числами. Теперь мы знаем, что такая связь есть, причём простые числа демонстрируют новый вид предельной перодичности — «эффективную» предельную периодичность, потому что синхронность в расстояниях между простыми числами по всей системе соблюдается только статистически.
Возникает вопрос: как закономерности в распределении простых чисел могут сказаться на стойкости криптографических алгоритмов?
«Я получаю действительно много писем на эту тему. Хотя это интересное исследование, но оно не имеет отношения к криптографии, — написал в своём блоге известный криптограф Брюс Шнайер. — Криптографам не интересен поиск простых чисел или даже их распределение. Стойкость алгоритмов криптографии с открытым ключом типа RSA связана со сложностью факторизации больших составных чисел, которые являются произведением простых чисел. А это совершенно другое дело».
Так что несмотря на прогресс в изучении распределения простых чисел, пока не стоит волноваться за стойкость криптошифров.

Комментариев нет:
Отправить комментарий