
Современная DDR3 SDRAM. Источник: BY-SA/4.0 by Kjerish
Во время недавнего посещения Музея компьютерной истории в Маунтин-Вью моё внимание привлёк древний образец ферритовой памяти.

Источник: BY-SA/3.0 by Konstantin Lanzet
Я быстро пришёл к выводу, что понятия не имею, как подобные штуки работают. Вращаются ли кольца (нет), и почему через каждое кольцо проходит три провода (я до сих пор не понимаю, как именно они работают). Что ещё более важно, я понял, что очень слабо представляю принцип работы современной динамической RAM!
Источник: Цикл Ульриха Дреппера о памяти
Меня особенно интересовало одно из следствий того, как работает динамическая RAM. Получается, что каждый бит данных хранится зарядом (или его отсутствием) на крошечном конденсаторе в микросхеме ОЗУ. Но эти конденсаторы постепенно теряют заряд со временем. Чтобы избежать потери сохранённых данных, они должны регулярно обновляться, чтобы восстановить заряд (если он есть) до первоначального уровня. Этот процесс обновления включает чтение каждого бита, а потом запись его обратно. В процессе такого «обновления» память занята и не может выполнять обычные операции, такие как запись или хранение битов.
Это долго беспокоило меня, и я задался вопросом… можно ли заметить задержку обновления на программном уровне?
Каждый модуль DIMM состоит из «ячеек» и «строк», «столбцов», «сторон» и/или «рангов». Эта презентация от Университета штата Юта объясняет номенклатуру. Конфигурацию памяти компьютера можно проверить командой
decode-dimms. Вот пример:
$ decode-dimms Size 4096 MB Banks x Rows x Columns x Bits 8 x 15 x 10 x 64 Ranks 2
Нам не нужно разбираться во всей схеме DDR DIMM, мы хотим понять работу только одной ячейки, хранящей один бит информации. А точнее, нас интересует только процесс обновления.
Рассмотрим два источника:
Каждый бит в динамической памяти должен обновляться: обычно это происходит каждые 64 мс (так называемое статическое обновление). Это довольно дорогостоящая операция. Чтобы избежать одной крупной остановки каждые 64 мс, процесс разделён на 8192 меньшие операции обновления. В каждой из них контроллер памяти компьютера отправляет команды обновления на микросхемы DRAM. После получения инструкции чип обновит 1/8192 ячеек. Если посчитать, то 64 мс / 8192 = 7812,5 нс или 7,81 мкс. Это значит следующее:
- Команда обновления выполняется каждые 7812,5 нс. Она называется tREFI.
- Процесс обновления и восстановления занимает некоторое время, поэтому чип может снова выполнять обычные операции чтения и записи. Так называемое tRFC равняется или 75 нс, или 120 нс (как в упомянутой документации Micron).
Если память горячая (более 85°C), то время хранения данных в памяти падает, а время статического обновления снижается вдвое до 32 Microsoft. Соответственно, tREFI падает до 3906,25 нс.
Типичная микросхема памяти занята обновлениями в течение значительной части времени своей работы: от 0,4% до 5%. Кроме того, чипы памяти отвечают за нетривиальную долю энергопотребления типичного компьютера, и большая часть этой мощности тратится на выполнение обновлений.
На время обновления блокируется вся микросхема памяти. То есть каждый бит в памяти заблокирован в течениее более 75 нс каждые 7812 нс. Давайте измерим.
Чтобы измерить операции с наносекундной точностью, нужен очень плотный цикл, возможно, на C. Он выглядит так:
for (i = 0; i < ...; i++) {
// Загрузка памяти. Любая инструкция загрузки делает
*(volatile int *) one_global_var;
// Очистка кэша CPU. Она относительно медленная
_mm_clflush(one_global_var);
// нужен барьер памяти, иначе иногда цикл может
// пройти очень быстро (25 нс вместо примерно 160).
// Думаю, из-за переупорядочивания.
asm volatile("mfence");
// Измерение и запись времени
clock_gettime(CLOCK_MONOTONIC, &ts);
}
Полный код доступен на GitHub.
Код очень простой. Выполняем чтение памяти. Сбрасываем данные из кэша CPU. Измеряем время.
(Примечание: во втором эксперименте я попытался для загрузки данных использовать MOVNTDQA, но это требует специальной некэшируемой страницы памяти и рутовых прав).
На моём компьютере программа выдаёт такие данные:
# метка времени, длительность цикла 3101895733, 134 3101895865, 132 3101896002, 137 3101896134, 132 3101896268, 134 3101896403, 135 3101896762, 359 3101896901, 139 3101897038, 137
Обычно получается цикл длительностью около 140 нс, периодически время подскакивает до примерно 360 нс. Иногда выскакивают странные результаты больше 3200 нс.
К сожалению, данные получаются слишком шумными. Очень трудно увидеть, есть ли заметная задержка, связанная с циклами обновления.
В какой-то момент меня осенило. Поскольку мы хотим найти событие с фиксированным интервалом, можно подать данные в алгоритм FFT (быстрое преобразование Фурье), который расшифрует основные частоты.
Я не первый, кто подумал об этом: Марк Сиборн со знаменитой уязвимостью Rowhammer реализовал эту самую технику ещё в 2015 году. Даже посмотрев код Марка, заставить FFT работать оказалось сложнее, чем я ожидал. Но в конце концов я собрал все кусочки воедино.
Сначала нужно подготовить данные. FFT требует входных данных с постоянным интервалом выборки. Мы также хотим обрезать данные, чтобы уменьшить шум. Методом проб и ошибок я обнаружил, что лучший результат достигается после предварительной обработки данных:
- Малые значения (меньше, чем 1,8 среднего) итераций цикла отрезаются, игнорируются и заменяются нулями. Мы действительно не хотим вводить шум.
- Все остальные показания заменяются единицами, так как нам действительно не важна амплитуда задержки, вызванной некоторым шумом.
- Я остановился на интервале выборки 100 нс, но подойдёт любое число до частоты Найквиста (двойная ожидаемая частота).
- Данные должны быть отобраны с фиксированным временем перед подачей в БПФ. Все разумные методы выборки работают нормально, я остановился на базовой линейной интерполяции.
Алгоритм примерно такой:
UNIT=100ns
A = [(timestamp, loop_duration),...]
p = 1
for curr_ts in frange(fist_ts, last_ts, UNIT):
while not(A[p-1].timestamp <= curr_ts < A[p].timestamp):
p += 1
v1 = 1 if avg*1.8 <= A[p-1].duration <= avg*4 else 0
v2 = 1 if avg*1.8 <= A[p].duration <= avg*4 else 0
v = estimate_linear(v1, v2, A[p-1].timestamp, curr_ts, A[p].timestamp)
B.append( v )
Который на моих данных производит довольно скучный вектор типа такого:
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...]
Впрочем, вектор довольно большой, обычно около 200 тыс. точек данных. С такими данными можно использовать FFT!
C = numpy.fft.fft(B)
C = numpy.abs(C)
F = numpy.fft.fftfreq(len(B)) * (1000000000/UNIT)
Довольно просто, правда? Это производит два вектора:
- C содержит комплексные числа частотных компонентов. Нас не интересуют комплексные числа, и можно сгладить их командой
abs(). - F содержит метки, какой частотный промежуток лежит в каком месте вектора C. Нормализуем показатель до герц умножением на частоту дискретизации входного вектора.
Результат можно нанести на диаграмму:
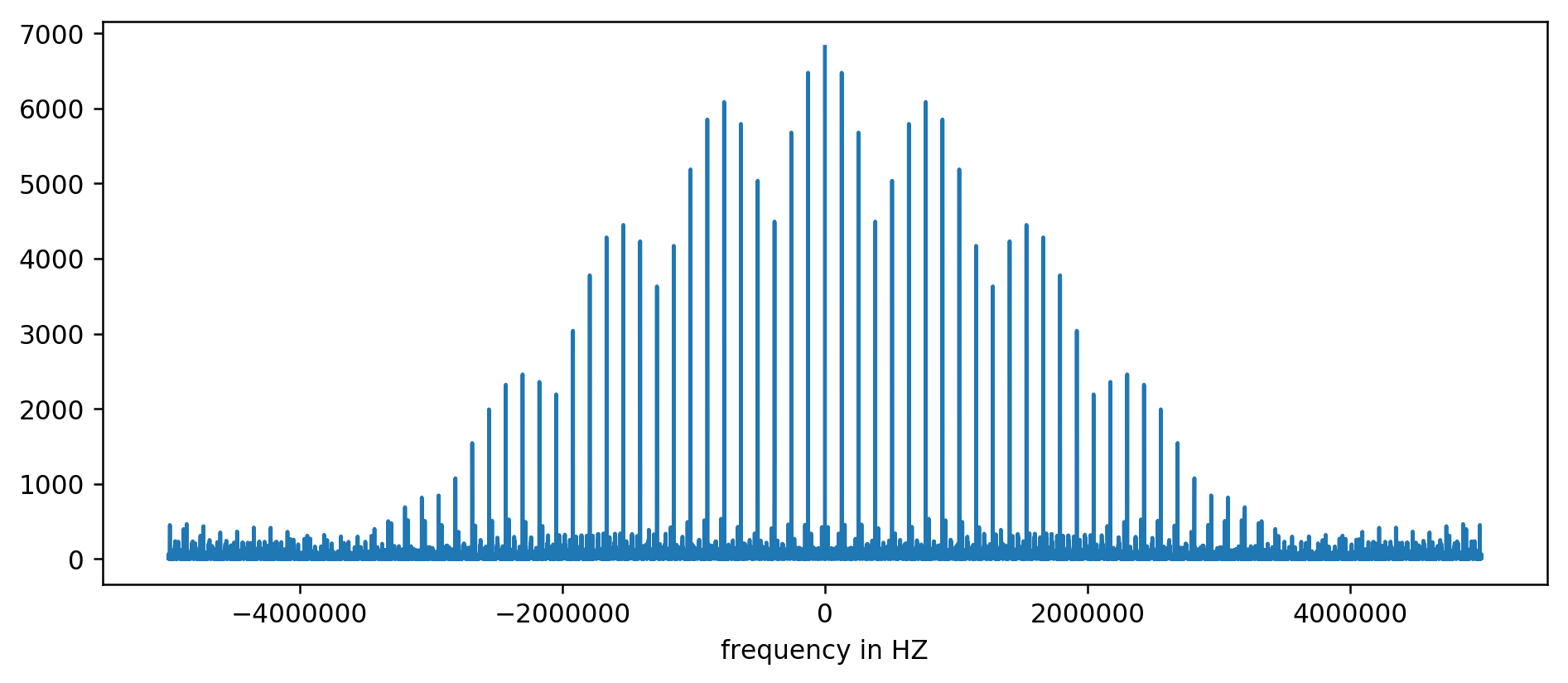
Ось Y без единиц измерения, поскольку мы нормализовали время задержки. Несмотря на это, чётко видны всплески в некоторых фиксированных интервалах частот. Рассмотрим их ближе:
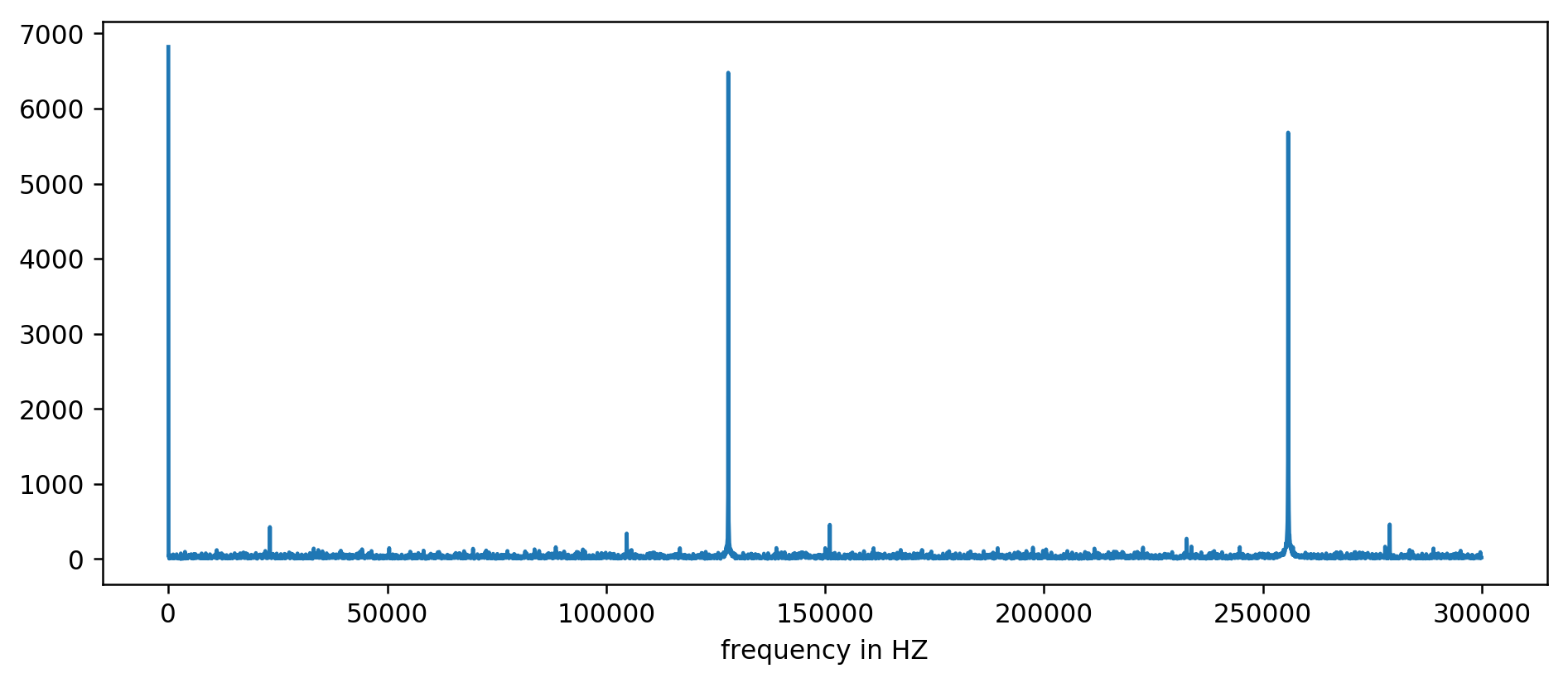
Мы ясно видим три первых пика. После немного невыразительный арифметики, включая фильтрацию чтения как минимум в десятикратном размере среднего, можно извлечь базовые частоты:
127850.0 127900.0 127950.0 255700.0 255750.0 255800.0 255850.0 255900.0 255950.0 383600.0 383650.0
Считаем: 1000000000 (нс/с) / 127900 (Гц) = 7818,6 нс
Ура! Первый скачок частоты — это действительно то, что мы искали, и он действительно коррелирует со временем обновления.
Остальные пики на 256 кГц, 384 кГц, 512 кГц — это так называемые гармоники, кратные нашей базовой частоте 128 кГц. Это полностью ожидаемый побочный эффект применения FFT на чём-то вроде прямоугольной волны.
Для облегчения экспериментов мы сделали версию для командной строки. Можете самостоятельно запустить код. Вот пример запуска на моём сервере:
~/2018-11-memory-refresh$ make gcc -msse4.1 -ggdb -O3 -Wall -Wextra measure-dram.c -o measure-dram ./measure-dram | python3 ./analyze-dram.py [*] Verifying ASLR: main=0x555555554890 stack=0x7fffffefe2ec [ ] Fun fact. I did 40663553 clock_gettime()'s per second [*] Measuring MOVQ + CLFLUSH time. Running 131072 iterations. [*] Writing out data [*] Input data: min=117 avg=176 med=167 max=8172 items=131072 [*] Cutoff range 212-inf [ ] 127849 items below cutoff, 0 items above cutoff, 3223 items non-zero [*] Running FFT [*] Top frequency above 2kHz below 250kHz has magnitude of 7716 [+] Top frequency spikes above 2kHZ are at: 127906Hz 7716 255813Hz 7947 383720Hz 7460 511626Hz 7141
Должен признать, код не совсем стабилен. В случае проблем рекомендуется отключить Turbo Boost, масштабирование частоты CPU и оптимизацию для производительности.
Из этой работы есть два основных вывода.
Мы увидели, что данные низкого уровня довольно трудно анализировать и они кажутся довольно шумными. Вместо оценки невооружённым глазом всегда можно использовать старый добрый БПФ. При подготовке данных необходимо в каком-то смысле принять желаемое за действительное.
Самое главное, мы показали, что зачастую возможно измерить тонкое аппаратное поведение из простого процесса в пользовательском пространстве. Такого рода мышление привело к открытию оригинальной уязвимости Rowhammer, оно реализовано в атаках Meltdown/Spectre и снова показано в недавней реинкарнации Rowhammer для памяти ECC.
Многое осталось за рамками данной статьи. Мы едва коснулись внутренней работы подсистемы памяти. Для дальнейшего чтения рекомендую:
Наконец, вот хорошее описание старой ферритовой памяти:
Комментариев нет:
Отправить комментарий