
Начнём с одного из самых главных понятий в контексте статьи – аффинные преобразования. Аффинные преобразования – это, по сути, преобразование системы координат (или пространства) с помощью умножения вектора на специальную матрицу. К примеру, такие преобразования, как перемещение, поворот, масштабирование, отражение и др. Основным свойствами аффинных преобразований является то, что вы остаётесь в том же пространстве (невозможно сделать из трёх мерного вектора двумерный) и то, что если прямые пересекались/были параллельны/скрещивались до преобразования, то это свойство после преобразования сохранится. Помимо этого, у них очень много математических свойств, которые требуют знания теории групп, множеств и линейной алгебры, что позволяет работать с ними проще.
TRS матрица
Вторым важным понятием в компьютерной графике является TRS матрица. С помощью неё можно описать самые частые операции, используемые при работе с компьютерной графикой. TRS матрица – это композиция трёх матриц преобразования. Матрицы перемещения (Translation), поворота по каждой оси (Rotation) и масштабирования (Scale).
Выглядит она так.
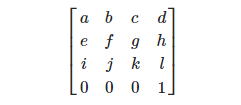
Где:
Перемещение – это t = new Vector3(d, h, l).
Масштабирование – s = new Vectro3(new Vector3(a, e, i).magnitude, new Vector3(b, f, j).magnitude, new Vector3(c, g, k).magnitude);
Поворот – это матрица вида:
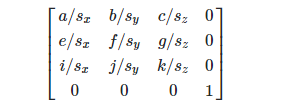
А теперь перейдём чуть глубже к контексту Unity. Начнём с того, что TRS матрица – это очень удобная вещь, но ей не стоит пользоваться везде. Так как простое указание позиции или сложение векторов в юнити будет работать быстрее, но во многих математических алгоритмов матрицы в разы удобнее векторов. Функционал TRS в Unity во многом реализован и в классе Matrix4x4, но он не удобен с точки зрения применения. Так как помимо применения матрицы через умножение она может в целом хранить в себе информацию об ориентации объекта, а также для некоторых преобразований хочется иметь возможность рассчитывать не только позицию, а изменять ориентацию объекта в целом (к примеру отражение, которое в Unity не реализовано)
Все примеры ниже приведены для локальной системы координат (началом координат считается позиция GameObject’а, внутри которого находится объект. Если объект является корнем иерархии в юнити, то начало координат – это мировые (0,0,0)).
Так как с помощью TRS матрицы можно в принципе описать положения объекта в пространстве, то нам нужна декомпозиция из TRS в конкретные значения position, rotation и scale для Unity. Для этого можно написать методы-расширения для класса Matrix4x4
public static Vector3 ExtractPosition(this Matrix4x4 matrix)
{
Vector3 position;
position.x = matrix.m03;
position.y = matrix.m13;
position.z = matrix.m23;
return position;
}
public static Quaternion ExtractRotation(this Matrix4x4 matrix)
{
Vector3 forward;
forward.x = matrix.m02;
forward.y = matrix.m12;
forward.z = matrix.m22;
Vector3 upwards;
upwards.x = matrix.m01;
upwards.y = matrix.m11;
upwards.z = matrix.m21;
return Quaternion.LookRotation(forward, upwards);
}
public static Vector3 ExtractScale(this Matrix4x4 matrix)
{
Vector3 scale;
scale.x = new Vector4(matrix.m00, matrix.m10, matrix.m20, matrix.m30).magnitude;
scale.y = new Vector4(matrix.m01, matrix.m11, matrix.m21, matrix.m31).magnitude;
scale.z = new Vector4(matrix.m02, matrix.m12, matrix.m22, matrix.m32).magnitude;
return scale;
}
Кроме того, для удобной работы можно реализовать пару расширений класса Transform, чтобы работать в нём с TRS.
public static void ApplyLocalTRS(this Transform tr, Matrix4x4 trs)
{
tr.localPosition = trs.ExtractPosition();
tr.localRotation = trs.ExtractRotation();
tr.localScale = trs.ExtractScale();
}
public static Matrix4x4 ExtractLocalTRS(this Transform tr)
{
return Matrix4x4.TRS(tr.localPosition, tr.localRotation, tr.localScale);
}
На этом плюсы юнити заканчиваются, так как матрицы в Unity очень бедны на операции. Для многих алгоритмов необходима матричная арифметика, которая в юнити не реализована даже в совершенно базовых операциях, таких как сложение матриц и умножения матриц на скаляр. Кроме того, из-за особенности реализации векторов в Unity3d, так же есть, ряд неудобств, связанных с тем, что вы можете сделать вектор 4х1, но не можете сделать 1х4 из коробки. Так как дальше пойдёт речь про преобразование Хаусхолдера для отражений, то сначала реализуем необходимые для этого операции.
По сложению/вычитанию и умножению на скаляр – всё просто. Выглядит достаточно громоздко, но ничего сложного тут нет, так как арифметика простая.
public static Matrix4x4 MutiplyByNumber(this Matrix4x4 matrix, float number)
{
return new Matrix4x4(
new Vector4(matrix.m00 * number, matrix.m10 * number, matrix.m20 * number, matrix.m30 * number),
new Vector4(matrix.m01 * number, matrix.m11 * number, matrix.m21 * number, matrix.m31 * number),
new Vector4(matrix.m02 * number, matrix.m12 * number, matrix.m22 * number, matrix.m32 * number),
new Vector4(matrix.m03 * number, matrix.m13 * number, matrix.m23 * number, matrix.m33 * number)
);
}
public static Matrix4x4 DivideByNumber(this Matrix4x4 matrix, float number)
{
return new Matrix4x4(
new Vector4(matrix.m00 / number, matrix.m10 / number, matrix.m20 / number, matrix.m30 / number),
new Vector4(matrix.m01 / number, matrix.m11 / number, matrix.m21 / number, matrix.m31 / number),
new Vector4(matrix.m02 / number, matrix.m12 / number, matrix.m22 / number, matrix.m32 / number),
new Vector4(matrix.m03 / number, matrix.m13 / number, matrix.m23 / number, matrix.m33 / number)
);
}
public static Matrix4x4 Plus(this Matrix4x4 matrix, Matrix4x4 matrixToAdding)
{
return new Matrix4x4(
new Vector4(matrix.m00 + matrixToAdding.m00, matrix.m10 + matrixToAdding.m10,
matrix.m20 + matrixToAdding.m20, matrix.m30 + matrix.m30),
new Vector4(matrix.m01 + matrixToAdding.m01, matrix.m11 + matrixToAdding.m11,
matrix.m21 + matrixToAdding.m21, matrix.m31 + matrix.m31),
new Vector4(matrix.m02 + matrixToAdding.m02, matrix.m12 + matrixToAdding.m12,
matrix.m22 + matrixToAdding.m22, matrix.m32 + matrix.m32),
new Vector4(matrix.m03 + matrixToAdding.m03, matrix.m13 + matrixToAdding.m13,
matrix.m23 + matrixToAdding.m23, matrix.m33 + matrix.m33)
);
}
public static Matrix4x4 Minus(this Matrix4x4 matrix, Matrix4x4 matrixToMinus)
{
return new Matrix4x4(
new Vector4(matrix.m00 - matrixToMinus.m00, matrix.m10 - matrixToMinus.m10,
matrix.m20 - matrixToMinus.m20, matrix.m30 - matrixToMinus.m30),
new Vector4(matrix.m01 - matrixToMinus.m01, matrix.m11 - matrixToMinus.m11,
matrix.m21 - matrixToMinus.m21, matrix.m31 - matrixToMinus.m31),
new Vector4(matrix.m02 - matrixToMinus.m02, matrix.m12 - matrixToMinus.m12,
matrix.m22 - matrixToMinus.m22, matrix.m32 - matrixToMinus.m32),
new Vector4(matrix.m03 - matrixToMinus.m03, matrix.m13 - matrixToMinus.m13,
matrix.m23 - matrixToMinus.m23, matrix.m33 - matrixToMinus.m33)
);
}
Но для отражения нам понадобится операция умножения матриц в конкретном частном случае. Умножение вектора размерности 4х1 на 1х4 (транспонированный) Если вы знакомы с матричной математикой, то знаете, что при таком умножении надо смотреть на крайние цифры размерности, и вы получите размерность матрицы на выходе, то есть в данном случае 4х4. Информации по тому, как перемножаются матрицы достаточно, поэтому это расписывать не будем. Вот для примера реализованный конкретный случай, который нам пригодится в будущем
public static Matrix4x4 MultiplyVectorsTransposed(Vector4 vector, Vector4 transposeVector)
{
float[] vectorPoints = new[] {vector.x, vector.y, vector.z, vector.w},
transposedVectorPoints = new[]
{transposeVector.x, transposeVector.y, transposeVector.z, transposeVector.w};
int matrixDimension = vectorPoints.Length;
float[] values = new float[matrixDimension * matrixDimension];
for (int i = 0; i < matrixDimension; i++)
{
for (int j = 0; j < matrixDimension; j++)
{
values[i + j * matrixDimension] = vectorPoints[i] * transposedVectorPoints[j];
}
}
return new Matrix4x4(
new Vector4(values[0], values[1], values[2], values[3]),
new Vector4(values[4], values[5], values[6], values[7]),
new Vector4(values[8], values[9], values[10], values[11]),
new Vector4(values[12], values[13], values[14], values[15])
);
}
Преобразование Хаусхолдера
В поисках того, как отразить объект относительно какой-либо оси, я часто встречаю совет поставить отрицательный scale по необходимому направлению. Это очень плохой совет в контексте Unity, так как он ломает очень много систем в движке (батчинг, коллизии и др.) В некоторых алгоритмах это превращается в достаточно нетривиальные вычисления, если вам надо отразить не банально относительно Vector3.up или Vector3.forward, а по произвольному направлению. Сам метод отражения в юнити из коробки не реализован, поэтому я реализовал метод Хаусхолдера.
Преобразование Хаусхолдера, используется не только в компьютерной графике, но в этом контексте — это линейное преобразование, которое отражает объект относительно плоскости, которая проходит через «начало координат» и определяется нормалью к плоскости. Во многих источниках оно описано достаточно сложно, и непонятно, хотя его формула – элементарна.
H=I-2*n* (n^T)
Где H – матрица преобразования, I в нашем случае – это Matrix4x4.identity, а n = new Vector4(planeNormal.x, planeNormal.y, planeNormal.z, 0). Символ T означает транспонирование, то есть после умножения n* (n^T) мы получим матрицу 4х4.
Тут пригодятся реализованные методы и запись получится очень компактной.
public static Matrix4x4 HouseholderReflection(this Matrix4x4 matrix4X4, Vector3 planeNormal)
{
planeNormal.Normalize();
Vector4 planeNormal4 = new Vector4(planeNormal.x, planeNormal.y, planeNormal.z, 0);
Matrix4x4 householderMatrix = Matrix4x4.identity.Minus(
MultiplyVectorsTransposed(planeNormal4, planeNormal4).MutiplyByNumber(2));
return householderMatrix * matrix4X4;
}
Важно: planeNormal должна быть нормализована (что логично), а также последней координатой n стоит 0, чтобы не было эффекта растяжения по направлению, так как оно зависит от длинны вектора n.
Теперь для удобства работы в Unity реализуем метод расширение для трансформа
public static void LocalReflect(this Transform tr, Vector3 planeNormal)
{
var trs = tr.ExtractLocalTRS();
var reflected = trs.HouseholderReflection(planeNormal);
tr.ApplyLocalTRS(reflected);
}
На этом на сегодня всё, если этот цикл статей и дальше будет интересен, то буду раскрывать и другие применения математики в разработке игр. В этот раз проекта не будет, так как весь код помещается в статье, но проект с конкретным применением будет в следующей статье. По картинке можно догадаться о чём будет следующая статья.

Спасибо за внимание!
Комментариев нет:
Отправить комментарий