[Перевод] GLSL: Центр или центроид? Или когда шейдеры атакуют

Дорабатывая шейдер для готовящейся к выходу игры, я столкнулся с неприятным артефактом, который проявляется только при включении аппаратного MSAA. На скриншоте ландшафта видно несколько чересчур ярких пикселей. Значения цвета в нескольких из них было настолько велико, что после наложения блума они превратились в разноцветных «призраков».

Предлагаю вашему вниманию перевод статьи, которая детально объясняет причину этого феномена и способ борьбы с ним.

Рисунок 1 — Корректное (слева) и некорректное (справа) изображения. Обратите внимание на жёлтую полосу у левого края «некорректного» изображения. Хотя переменная myMixer изменяется от 0 до 1, каким то образом она выходит за пределы этого диапазона на «некорректном» изображении.

Рассмотрим простой фрагментный шейдер с простым нелинейным преобразованием:

smooth in float myMixer;

// Интерполируем цвет между синим и жёлтым.
// Используем sqrt для более вычурного эффекта.
void main( void )
{
    const vec3 blue   = vec3( 0.0, 0.0, 1.0 );
    const vec3 yellow = vec3( 1.0, 1.0, 0.0 );
    float a = sqrt( myMixer ); // не определено при myMixer < 0.0
    vec3 color = mix( blue, yellow, a ); // нелинейная интерполяция
    gl_FragColor = vec4( color, 1.0 );
}

Откуда взялась жёлтая полоса слева на некорректном изображении? Чтобы лучше понимать что пошло не так, давайте сначала рассмотрим случай, в котором все работает правильно (почти) всегда.

Это классическая растеризация с одной выборкой. Серые квадраты представляют собой пиксели, а жёлтые точки — центры пикселей, расположенные в полуцелых оконных координатах (по умолчанию координаты левого нижнего пикселя в gl_FragCoord равны (0.5, 0.5) — перев.).

На картинке выше секущая линия отделяет полупространство примитива. Выше и левее этой линии переменная myMixer положительна, а ниже и правее — отрицательна.

Классическая одновыборочная растеризация классифицирует пиксели по принадлежности к примитиву, и создаёт фрагменты только для пикселей, центры которых лежат внутри примитива. В этом примере будет произведено шесть фрагментов, показанных вверху слева. Пиксели, отмеченные приглушённым цветом, не попадают в примитив. Для них не будут сгенерированы фрагменты.

Зелёным отмечены точки, в которых будет вычисляться фрагментный шейдер. Значение myMixer будет вычислено для центра каждого пикселя. Обратите внимание, что зелёные точки находятся выше и левее линии, поэтому значения myMixer в них будут положительными. Все входные данные, ассоциированные с вершинами (varying или in/out-переменные), так же будут интерполированы в этих точках.

Наш простой шейдер не использует производные (явные или неявные, например при выборке из текстуры с mip-уровнями), однако стрелками отемечены производные dFdx (горизонтальная) и dFdy (вертикальная). Внутри примитива они достаточно хорошо определены и регулярны.

Подведём итог: при одиночной выборке фрагменты генерируются только если центр пикселя попадает «внутрь» примитива, данные фрагмента вычисляются для центра пикселя, интерполяция вершинных данных и вычисление шейдера выполняются только внутри примитива. Всё хорошо и «корректно». (Почти всегда. Пока опустим неточности некоторых производных на пикселях вдоль границы примитива).

Итак, все (почти) отлично при растеризации с одной выборкой. Но что может пойти не так при включении мультисемплинга?

Это классическая растеризация с мультисемплингом. Серыми квадратами обозначены пиксели. Жёлтые точки — центры пикселей в полуцелых координатах. В синих точках происходит выборка. В этом примере показана простая схема из двух выборок с поворотом. Все рассуждения можно обобщить для произвольного количества выборок.

Линия по-прежнему отделяет полупространство примитива. Выше и левее неё значение myMixer положительно. Ниже и правее — отрицательно.

При растеризации с мультисемплингом классификатор пикселей сгенерирует фрагмент, если хотя бы один семпл пикселя попадает внутрь примитива.

В этом примере будет сгенерировано 10 фрагментов, показанных в верхней левой полуплоскости. Обратите внимание на добавившиеся четыре фрагмента вдоль грани, у которых одна выборка попадает внутрь примитива, хотя центр находится снаружи. Пиксели вне примитива по-прежнему отмечены тусклым.

Что будет при вычислении в центре пикселя?

Шейдер будет вычислен в зелёных и красных точках для каждого из фрагментов. Ассоциированные данные myMixer вычисляются в центре каждого пикселя. В зелёных точках эти значения будут положительными, так как они выше и левее границы. Красные точки находятся вне примитива, потому значения myMixer в них отрицательны. В красных точках ассоциированные данные экстраполируются вместо интерполирования.

В нашем шейдере значения sqrt(myMixer) не определены при отрицательном myMixer. Даже когда значения myMixer, записанные вершинным шейдером, лежат в отрезке от нуля до единицы, во фрагментом шейдере myMixer может выходит за этот отрезок из-за экстраполяции. Таким образом, при отрицательном myMixer результат работы фрагментного шейдера не определён.

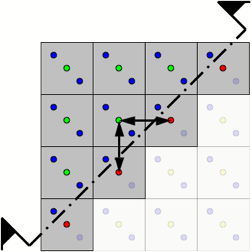
Мы по-прежнему рассматриваем вычисление шейдера в центрах пикселей, стрелки на рисунке показывают dFdx и dFdy. На внутренних фрагментах полигона они достаточно хорошо определены потому что все вычисления делаются в центрах пикселей, расположенных через равные промежутки.

Что будет при вычислении в точках, отличных от центров пикселей?

Зелёными отмечены точки, в которых будет вычислен шейдер. Ассоциированное значение myMixer вычисляется в центроиде каждого пикселя.

Центроид пикселя — это центр тяжести пересечения квадрата пикселя и внутренности примитива. Для полностью покрытого пикселя центроид совпадает с центром. Для частично покрытого пикселя центроид как правило отличается от центра.

Стандарт OpenGL позволяет реализации выбрать произвольную точку в пересечении примитива и пикселя вместо идеального центроида. Например, это может быть точка выборки.

В этом примере, если центр лежит внутри примитива, данные вершин вычисляются для центра. В противном случае они вычисляются в любой из точек выборки, лежащей внутри примитива. Так происходит для четырёх пикселей вдоль границы. Все зелёные точки лежат выше и левее границы, поэтому значения в них всегда интерполируются и никогда не экстраполируются.

Почему бы не вычислять шейдер в центроиде всегда? В общем случае, это дороже, чем вычисление в центре. Однако, это не главный фактор.

Всё дело в вычислении производных. Обратите внимание на стрелки между зелёными точками. Расстояние ними не одинаково для различных пар точек. Кроме того, y не является константой для dFdx, а x не постоянна для dFdy. Производные менее точны при вычислении в центроидах.

Это компромисс, а потому OpenGL, начиная с GLSL 1.20, предлагает разработчику шейдера выбор между центром и центроидом с помощью квалификатора centroid:

centroid in float myMixer; // Используем centroid вместо smooth

// Интерполируем цвет между синим и жёлтым.
// Используем sqrt для более вычурного эффекта.
void main( void )
{
    const vec3 blue   = vec3( 0.0, 0.0, 1.0 );
    const vec3 yellow = vec3( 1.0, 1.0, 0.0 );
    float a = sqrt( myMixer ); // не определено при myMixer < 0.0
    vec3 color = mix( blue, yellow, a ); // нелинейная интерполяция
    gl_FragColor = vec4( color, 1.0 );
}

Когда следует использовать centroid?

1. Когда экстраполированное значение может привести к неопределённым результатам. Обращайте особое внимание на встроенные функции, в описании которых сказано «результат не определён, если...»
2. Когда экстраполированное значение используется с очень нелинейной или имеющей разрыв функцией. К таковым относится функция step или вычисление блика, особенно когда показатель степени достаточно большой.

Когда не следует использовать центроид?

1. Если нужны точные производные. Производные могут быть как явными (вызов dFdx), так и неявными, например выборки из текстур с mip-уровнями или с анизотропной фильтрацией. В спецификации GLSL производные в центроидах считаются настолько негодными, что они были объявлены неопределёнными. В таких случаях старайтесь писать:

   centroid in float myMixer; // Опасайтесь производных!
   smooth in float myCenterMixer; // С производными всё в порядке.
   
   

   
   
2. Если рендерится сетка, в которой большинство границ примитивов являются внутренними и всегда хорошо определены. Простейший пример — полоса из 100 треугольников (TRIANGLE_STRIP), в которой только первый и последний треугольник подвержены экстраполяции. Квалификатор centroid приведёт к интерполяции на этих двух треугольниках ценой потери точности и непрерывности на остальных 98 треугольниках.
3. Если вы знаете, что могут появиться артефакты от неопределённой, нелинейной или разрывной функции, но на практике эти артефакты получаются почти невидимыми. Если шейдер не атакует — не исправляйте его!

Let's block ads! (Why?)