За последние несколько лет исследователи ИИ достигали всё больше успеха в ускорении обучения нейросети при помощи распараллеливания данных, разбивающего большие пакеты данных на несколько компьютеров. Исследователи успешно использовали пакеты размером в десятки тысяч единиц для классификации изображений и моделирования языка, и даже в миллионы агентов обучения с подкреплением, игравших в Dota 2. Такие большие пакеты позволяют увеличивать объёмы вычислительных мощностей, которые эффективно участвуют в обучении одной модели, и являются одной из сил, движущих рост в области обучения ИИ. Однако со слишком большими пакетами данных происходит быстрое уменьшение алгоритмической отдачи, и непонятно, почему эти ограничения оказываются крупнее для одних задач и мельче для других.
Масштабирование градиентного шума, усреднённое по подходам к обучению, объясняет большую часть (r2 = 80%) вариаций размера критического пакета данных на различных задачах, отличающихся на шесть порядков. Размеры пакетов измеряются в количестве изображений, токенов (для языковых моделей) или наблюдений (для игр).
Мы обнаружили, что, измеряя масштаб градиентного шума, простую статистику, численно определяющую соотношение сигнал/шум в градиентах сети, мы можем приблизительно предсказать максимальный размер пакета. Эвристически, шкала шума измеряет вариацию данных с точки зрения модели (на определённом этапе обучения). Когда шкала шума мала, параллельное обучение на большом количестве данных быстро становится избыточным, а когда она велика, мы можем обучиться многому на крупных наборах данных.
Статистика такого рода широко используется для определения размера выборки, и её предлагали использовать в глубинном обучении, однако её не применяли систематически для современного обучения нейросетей. Мы подтвердили это предсказание для большого спектра задач машинного обучения, изображённых на графике выше, включая распознавание образов, моделирование языка, игры Atari и Dota. В частности, мы провели обучение нейросетей, предназначенных для решения каждой из этих задач, на пакетах данных разнообразного размера (отдельно подстраивая скорость обучения для каждого из них), и сравнили ускорение обучения с тем, что предсказывает масштаб шума. Поскольку пакеты данных крупного размера часто требуют тщательной и затратной подстройки или специального графика скорости обучения для того, чтобы обучение прошло эффективно, заранее зная верхнее ограничение, можно получить значительное преимущество при обучении новых моделей.
Мы нашли полезным визуализировать результаты этих экспериментов как компромисс между фактическим временем обучения, и общим объёмом вычислений, потребовавшимся для обучения (пропорциональным его стоимости в деньгах). На очень мелких пакетах данных удвоение размера пакета позволяет проводить обучение в два раза быстрее без использования дополнительных вычислительных мощностей (мы запускаем в два раза больше отдельных потоков, которые отрабатывают в два раза быстрее). На очень крупных макетах данных параллелизация не даёт ускорения обучения. Кривая в середине прогибается, и масштаб градиентного шума предсказывает, где именно происходит прогиб.
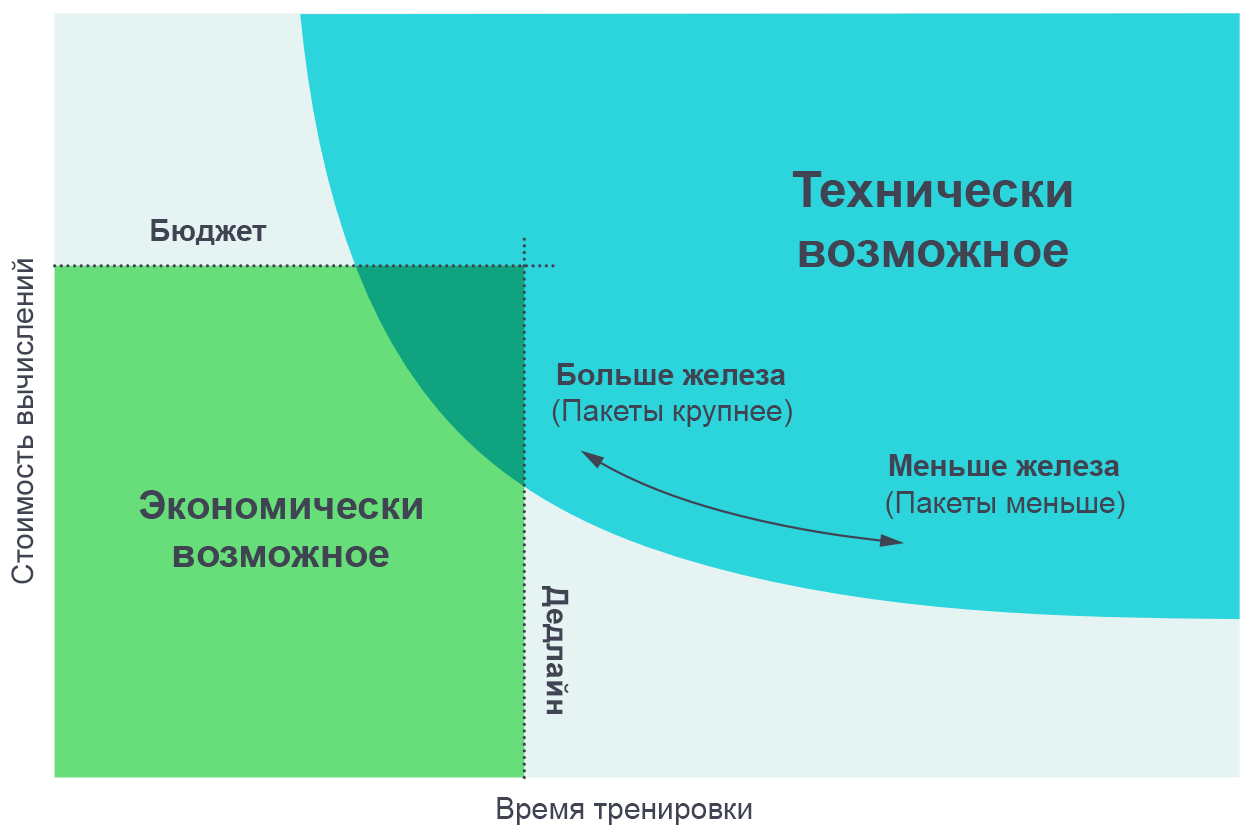 Увеличение количества параллельных процессов позволяет обучать более сложные модели в разумное время. Пограничная диаграмма Парето – наиболее интуитивный способ визуализации сравнения алгоритмов и масштабов.
Увеличение количества параллельных процессов позволяет обучать более сложные модели в разумное время. Пограничная диаграмма Парето – наиболее интуитивный способ визуализации сравнения алгоритмов и масштабов.
Эти кривые мы получаем, назначая цель в задаче (допустим, 1000 очков в игре Beam Rider от Atari), и наблюдая за тем, как долго нужно обучаться нейросети, чтобы достичь этой цели на разных размерах пакетов. Результаты достаточно точно совпадают с предсказаниями нашей модели, с учётом различных величин устанавливаемых нами целей.
[На странице с оригинальной статьёй представлены интерактивные графики компромисса между опытом и временем обучения, необходимыми для достижения заданной цели]
Закономерности масштаба градиентного шума
Мы наткнулись на несколько закономерностей в масштабе градиентного шума, на основе которых можно делать предположения по поводу будущего обучения ИИ.
Во-первых, в наших экспериментах в процессе обучения масштаб шума обычно увеличивается на порядок или более. Судя по всему, это означает, что сеть обучается более «очевидным» особенностям задачи в самом начале обучения, а затем изучает более мелкие детали. К примеру, в задаче классификации изображений нейросеть сначала может обучиться определять особенности мелкого масштаба, вроде краёв или текстур, представленных на большинстве изображений, и лишь позже сопоставлять эти мелочи вместе, создавая более общие концепции, вроде кошек или собак. Чтобы получить представление о всём разнообразии граней и текстур, нейросети нужно увидеть небольшое количество изображений, поэтому масштаб шума меньше; как только сеть будет знать больше по поводу более крупных объектов, она сможет обрабатывать гораздо больше изображений одновременно, не рассматривая дублирующиеся данные.
Мы увидели несколько предварительных указаний на то, что сходный эффект работает и на других моделях, имеющих дело с тем же набором данных – у более мощных моделей масштаб градиентного шума выше, но только потому, что у них меньше потери. Поэтому есть некоторые свидетельства того, что увеличение масштаба шума во время обучения является не просто артефактом сходимости, но происходит из-за улучшения модели. Если это так, то мы можем ожидать, что будущие, улучшенные модели, будут обладать большим масштабом шума и будут лучше поддаваться параллелизации.
Во-вторых, задачи, объективно более сложные, лучше поддаются параллелизации. В контексте обучения с учителем, виден явный прогресс при переходе от MNIST к SVHN и ImageNet. В контексте обучения с подкреплением виден явный прогресс при переходе от Atari Pong к Dota 1v1 и Dota 5v5, причём размер оптимального пакета данных варьируется в 10 000 раз. Поэтому, по мере того, как ИИ будет справляться со всё более сложными задачами, ожидается, что модели станут справляться с наборами данных всё большего размера.
Последствия
Степень параллелизации данных серьёзно влияет на скорость развития возможностей ИИ. Ускорение обучения делает возможным создание более способных моделей и ускоряет исследования, позволяя укорачивать время каждой итерации.
В более раннем исследовании, "ИИ и расчёты", мы видели, что расчёты для обучения крупнейших моделей удваиваются каждые 3,5 месяце, и отметили, что эта тенденция основывается на комбинации экономики (желания тратить деньги на расчёты) и алгоритмических возможностях по параллелизации обучения. Последний фактор (алгоритмическая параллелизуемость) предсказать сложнее, а его ограничения ещё не изучены до конца, но наши текущие результаты представляют шаг вперёд в деле его систематизации и численного выражения. В частности, у нас есть свидетельства того, что более сложные задачи, или более мощные модели, направленные на известную задачу, позволят сильнее распараллеливать работу с данными. Это будет ключевым фактором, поддерживающим экспоненциальный рост вычислений, связанных с обучением. И мы даже не рассматриваем недавние разработки в области параллельных моделей, которые могут позволить ещё больше усилить параллелизацию, добавив её к существующей параллельной обработке данных.
Продолжение роста области обучающих вычислений и её предсказуемая алгоритмическая база говорят о возможности взрывного увеличения возможностей ИИ в следующие несколько лет, и подчёркивают необходимость скорейшего исследования безопасного и ответственного использования подобных систем. Главной трудностью создания политики использования ИИ будет решить, как можно использовать подобные меры дл того, чтобы предсказывать характеристики будущих ИИ-систем, и использовать это знание для создания правил, позволяющих обществу максимизировать полезные свойства и минимизировать вред этих технологий.
Организация OpenAI планирует проводить строгий анализ, позволяющий предсказывать будущее ИИ, и упреждающе работать с проблемами, поднимаемыми этим анализом.
Комментариев нет:
Отправить комментарий