
Итак, пришло время поговорить о следующем поколении мультиклеточных процессоров: MultiClet S1. Если вы впервые слышите о них, то обязательно ознакомьтесь с историей и идеологией архитектуры в этих статьях:
На данный момент новый процессор находится в разработке, но уже появились первые результаты и можно оценить, на что он будет способен.
Начнём, пожалуй, с самых больших изменений: базовых характеристик.
Характеристики.
Планируется достичь следующих показателей:
- Количество клеток: 64
- Техпроцесс: 28 нм
- Тактовая частота: 1.6 ГГц
- Размер памяти на кристалле: 8 Мб
- Площадь кристалла: 40мм2
- Энергопотребление: 6 Вт
Реальные цифры будут анонсированы по результатам тестов изготовленных образцов в 2019 году. Помимо характеристик самого кристалла, процессор будет поддерживать до 16 Гб RAM стандарта DDR4 3200MHz, шину PCI Express и PLL.
Надо заметить, что техпроцесс 28 нм – это самый низкий бытовой диапазон, не требующий специальных разрешений на использование, поэтому был выбран именно он. По количеству клеток рассматривались разные варианты: 128 и 256, но с увеличением площади кристалла растёт процент брака. Остановились на 64 клетках и, соответственно, сравнительно небольшой площади, что даст больший выход годных кристаллов на пластине. Дальнейшее развитие возможно в рамках СвК (система в корпусе), где можно будет объединить несколько 64-клеточных кристаллов в один корпус.
Необходимо сказать, что назначение и применение процессора кардинально меняется. S1 будет не предназначенным для встраивания микропроцессором, какими были P1 и R1, а ускорителем вычислений. Так же, как GPGPU, плату с S1 можно будет вставить в PCI Express материнской платы обычного ПК и использовать для обработки данных.
Архитектура
В S1 минимальной вычислительной единицей теперь выступает “мультиклетка”: набор из 4 клеток, исполняющих некую последовательность команд. Сначала планировали объединять мультиклетки в группы под названием кластер для совместного исполнения команд: кластер должен был содержать 4 мультиклетки, всего на кристалле 4 раздельных кластера. Однако, каждая клетка имеет полную связь со всеми остальными клетками в кластере, и при увеличении группы связей становится слишком много, что резко усложняет топологическое проектирование микросхемы и снижает её характеристики. Поэтому, приняли решение отказаться от кластерного деления, поскольку усложнение не оправдывает полученные результаты. К тому же, для максимальной производительности выгоднее всего запускать код параллельно на каждой мультиклетке. Итого, сейчас процессор содержит 16 раздельных мультиклеток.
Мультиклетка, хоть и состоит из 4 клеток, отличается от 4-клеточного R1, в котором каждая клетка имела свою память, свой блок выборки команд, своё ALU. S1 устроен немного по-другому. ALU имеет 2 части: блок арифметики с плавающей точкой и блок целочисленной арифметики. Каждая клетка имеет отдельный целочисленный блок, но блоков с плавающей точкой в мультиклетке только два, и поэтому две пары клеток делят их между собой. Сделано это было, в основном, для уменьшения площади кристалла: 64-битная арифметика с плавающей точкой, в отличие от целочисленной арифметики, занимает очень много места. Иметь такой блок ALU на каждой клетке оказалось избыточным: выборка команд не обеспечивает загрузки ALU и они простаивают. При сокращении числа блоков ALU и сохранении темпов выборки команд и данных, как показала практика, общее время решения задач практически не меняется или меняется незначительно, а блоки ALU загружаются полностью. К тому же, арифметика с плавающей точкой используется не так часто, как с целочисленной.
Схематический вид блоков процессоров R1 и S1 приведен на схеме ниже. Здесь:
- CU (Control Unit) – блок выборки инструкций
- ALUFX – арифметическо-логическое устройство целочисленной арифметики
- ALUFP – арифметическо-логическое устройство арифметики с плавающей точкой
- DMS (Data Memory Scheduler) – блок управления памятью данных
- DM – память данных
- PMS (Program Memory Scheduler) – блок управления памятью программ
- PM – память программ
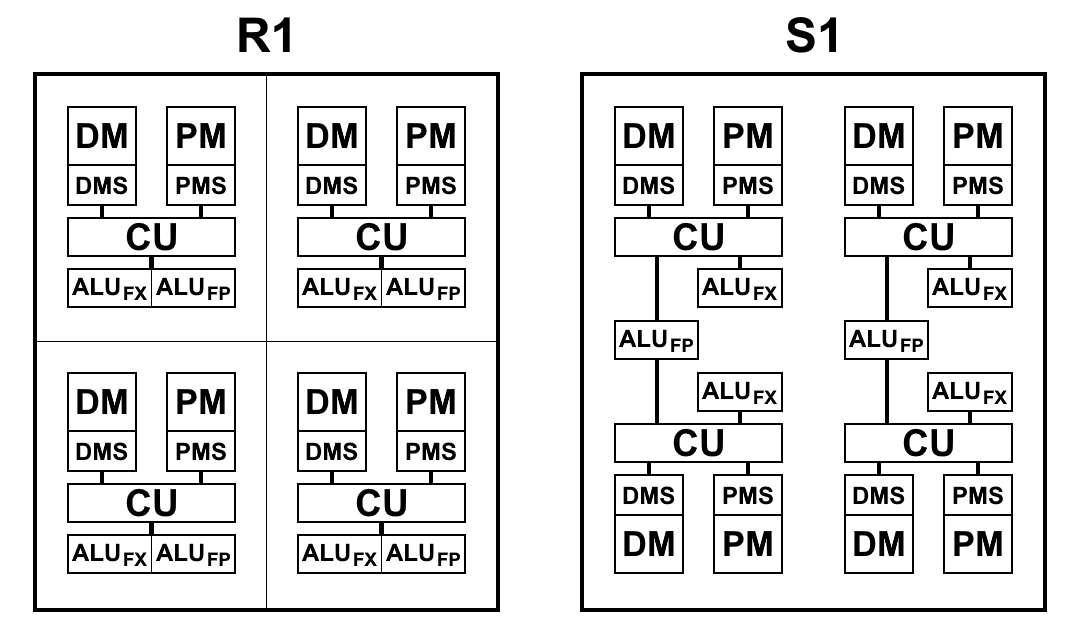
Архитектурные отличия S1:
- Команды теперь могут обращаться к результатам команд из предыдущих параграфов. Это очень важное изменение, позволяющее существенно ускорить переходы при ветвлении кода. В процессорах P1 и R1 не было другого выбора, кроме как записывать нужные результаты в память и тут же считывать их обратно первыми же командами в новом параграфе. Даже при использовании памяти на кристалле, операции записи и чтения занимают от 2 до 5 тактов каждая, которые можно сэкономить, просто обратившись к результату команды из предыдущего параграфа
- Запись в память и регистры теперь происходит сразу, а не по окончанию параграфа, что позволяет начать выполнение команд записи до окончания параграфа. В результате, уменьшается потенциальный простой между параграфами.
- Оптимизирована система команд, а именно:
- Добавлена 64-битная целочисленная арифметика: сложение, вычитание, умножение 32-битных чисел, возвращающее 64-битный результат.
- Изменен способ чтения из памяти: теперь для любой команды в качестве аргумента можно просто указать адрес, с которого нужно прочитать данные, при этом сохраняется очерёдность выполнения команд чтения и записи.
Это также сделало отдельную команду чтения из памяти устаревшей. Вместо этого, используется команда загрузки значения в коммутатор load (ранее – get), указывая в качестве аргумента адрес в памяти:
.data foo: .long 0x1234 .text habr: load_l foo ; загрузит в коммутатор адрес метки foo load_l [foo] ; загрузит в коммутатор 0x1234 add_l [foo], 0xABCD ; прочитать значение и сложить с константой ; одной командой complete - Добавлен формат команд, позволяющий использовать 2 константных аргумента.
Раньше можно было указывать константу только в качестве второго аргумента, первым аргументом всегда должна была быть ссылка на результат в коммутаторе. Изменение касается всех двухаргументных команд. Поле константы всегда 32 битное, поэтому такой формат позволяет, например, генерировать 64-битные константы одной командой.Было:
load_l 0x12345678 patch_q @1, 0xDEADBEEF
Стало:patch_q 0x12345678, 0xDEADBEEF - Изменены и дополнены векторные типы данных.
То, что раньше называлось «упакованными» типами данных теперь смело можно называть векторными. В P1 и R1 операции над упакованными числами принимали только константу в качестве второго аргумента, т.е., например, при сложении, каждый элемент вектора складывался с одним и тем же числом, и этому не нашлось толкового применения. Теперь аналогичные операции можно применять над двумя полноценными векторами. Более того, такой способ работы с векторами полностью соответствует механизму векторов в LLVM, что теперь позволит компилятору генерировать код с использованием векторных типов.patch_q 0x00010002, 0x00030004 patch_q 0x00020003, 0x00040005 mul_ps @1, @2 ; результат - 00020006000C0014
- Убраны процессорные флаги.
Как следствие, убрано около 40 команд, опирающихся исключительно на значения флагов. Это позволило значительно сократить количество команд и, соответственно, площадь кристалла. А вся необходимая информация теперь хранится непосредственно в ячейке коммутатора.
- При сравнении с нулём, вместо флага нуля теперь используется просто значение в коммутаторе
- Вместо флага знака теперь используется бит, соответствующий типу команды: 7й для byte, 15й для short, 31й для long, 63й для quad. Благодаря тому, что знак размножается вплоть до 63го бита вне зависимости от типа, можно сравнивать числа разных типов:
.data long: .long -0x1000 byte: .byte -0x10 .text habr: a := load_b [byte] ; В коммутатор попадет значение 0xFFFFFFFFFFFFFFF0, ; согласно типу byte 7й бит размножился до 63го. b := loadu_b [byte] ; В коммутатор попадет значение 0x00000000000000F0, ; т.к. команда loadu_b не размножает знак c := load_l [long] ; В коммутатор попадет значение 0xFFFFFFFFFFFFF000. ge_l @a, @c ; Результатом команды "больше либо равно" будет 1: ; сравнение учитывает 31й бит, согласно своему типу. lt_s @a, @b ; 1, т.к. b прочиталось как положительное число complete - Флаг переноса больше не нужен, так как есть 64-битная арифметика
- Сократилось время перехода с параграфа на параграф до 1 такта (вместо 2-3 в R1)
Компилятор на базе LLVM
Компилятор языка C для S1 аналогичен R1, и так как архитектура принципиально не изменилась, то и проблемы, описанные в предыдущей статье, к сожалению, не исчезли.
Однако, в процессе реализации новой системы команд количество выходного кода снизилось само по себе, просто благодаря обновлению системы команд. Помимо этого, есть ещё множество мелких оптимизаций, которые позволят сократить количество команд в коде, некоторые из которых уже сделаны (например, генерация 64-битных констант одной командой). Но есть ещё более серьёзные оптимизации, которые необходимо сделать, и их можно выстроить в порядке возрастания одновременно как эффективности, так и сложности реализации:
- Возможность генерации всех двухаргументных команд с двумя константами.
Генерация 64-битной константы через patch_q – это всего лишь частный случай, а нужен общий. На самом деле, смысл этой оптимизации в том, чтобы позволить командам подставлять именно первый аргумент как константу, так как второй аргумент всегда мог быть константой, и это давно реализовано. Это не слишком частый случай, но, например, когда нужно вызвать функцию и записать на вершину стека адрес возврата из неё, то можно
load_l func wr_l @1, #SP
оптимизировать доwr_l func, #SP - Возможность подставлять обращение к памяти через аргумент в любой команде.
Например, если нужно сложить два числа из памяти, можноload_l [foo] load_l [bar] add_l @1, @2
оптимизировать доadd_l [foo], [bar]
Эта оптимизация – расширение предыдущей, однако здесь уже нужен анализ: такую замену можно проводить только в том случае, если загруженные значения используется только один раз в этой команде сложения и нигде более. Если результат чтения используется даже всего в двух командах, то выгоднее прочитать из памяти один раз отдельной командой, а в остальных двух ссылаться на неё через коммутатор. - Оптимизация переноса виртуальных регистров между базовыми блоками.
Для R1 перенос всех виртуальных регистров был сделан через память, что порождает очень большое количество чтений и записей в память, но другого способа переносить данные между параграфами просто не было. S1 позволяет обращаться к результатам команд предыдущих параграфов, поэтому, теоретически, многие операции с памятью можно убрать, что дало бы наибольший эффект среди всех оптимизаций. Однако, такой подход все равно ограничен коммутатором: не более 63 предыдущих результатов, поэтому далеко не каждый перенос виртуального регистра можно так реализовать. Как это сделать – задача нетривиальная, и анализ возможностей ее решения еще только предстоит. Исходники компилятора, возможно, появятся в открытом доступе, поэтому если у кого-нибудь есть идеи, и вы желаете присоединиться к разработке, то вы сможете это сделать.
Бенчмарки
Так как процессор еще не выпущен на кристалле, сложно оценить его реальную производительность. Однако, RTL код ядра уже готов, а значит можно сделать оценку с помощью симуляции или FPGA. Для запуска следующих бенчмарков использовалась симуляция с помощи программы ModelSim, чтобы вычислить точное время выполнения (в тактах). Так как сделать симуляцию всего кристалла сложно и это занимает очень много времени, поэтому моделировалась одна мультиклетка, и результат умножался на 16 (если задача предназначена для многопоточности), поскольку каждая мультиклетка может работать совершенно независимо от других.
Параллельно проводилось моделирование мультиклетки на Xilinx Virtex-6 для проверки работоспособности процессорного кода на реальном железе.
CoreMark
CoreMark – набор тестов для комплексной оценки производительности микроконтроллеров и центральных процессоров, а также их C-компиляторов. Как вы можете заметить, процессор S1 не является ни тем, ни другим. Однако, он предназначен для исполнения абсолютно арбитрарного кода, т.е. любого, который мог бы быть запущен на центральном процессоре. А значит CoreMark подходит для оценки производительности S1 ничуть не хуже.
CoreMark содержит работу со связными списками, матрицами, машиной состояний и подсчетом суммы CRC. В общем, большинство кода получается строго последовательным (что проверяет на прочность мультиклеточный аппаратный параллелизм) и с множеством ветвлений, из-за чего возможности компилятора играют значительную роль в итоговой производительности. Откомпилированный код содержит довольно много коротких параграфов и несмотря на то, что скорость перехода между ними увеличилась, ветвление включает в себя работу с памятью, чего хотелось бы избегать по максимуму.
Сравнительная таблица показателей CoreMark:
| Multiclet R1 (llvm compiler) | Multiclet S1 (llvm compiler) | Эльбрус-4С (R500/E) | Texas Inst. AM5728 ARM Cortex-A15 | Baikal-T1 | Intel Core i7 7700K | |
|---|---|---|---|---|---|---|
| Год выпуска | 2015 | 2019 | 2014 | 2018 | 2016 | 2017 |
| Тактовая частота, МГц | 100 | 1600 | 700 | 1500 | 1200 | 4500 |
| Общий показатель CoreMark | 59 | 18356 | 1214 | 15789 | 13142 | 182128 |
| CoreMark/MHz | 0.59 | 11.47 | 5.05 | 10.53 | 10.95 | 40.47 |
Результат одной мультиклетки – 1147, или 0.72 / MHz, что выше, чем у R1. Это говорит о преимуществах развития мультиклеточной архитектуры в новом процессоре.
Whetstone
Whetstone – набор тестов для измерения производительности процессора при работе с числами с плавающей точкой. Здесь ситуация значительно лучше: код тоже последовательный, однако без большого количества ветвлений и с хорошим внутренним параллелизмом.
Whetstone состоит из множества модулей, что позволяет замерять не только общий результат, но и производительность на каждом конкретном модуле:
- Array elements
- Array as parameter
- Conditional jumps
- Integer arithmetic
- Trigonometric functions (tan, sin, cos)
- Procedure calls
- Array references
- Standard functions (sqrt, exp, log)
Они разбиваются на категории: модули 1, 2 и 6 измеряют производительность операций с плавающей точкой (строки MFLOPS1-3); модули 5 и 8 — математических функций (COS MOPS, EXP MOPS); модули 4 и 7 — целочисленной арифметики (FIXPT MOPS, EQUAL MOPS); модуль 3 — условных переходов (IF MOPS). В таблице ниже вторая строка MWIPS – общий показатель.
В отличие от CoreMark, Whetstone будет сравниваться на одном ядре или, как в нашем случае, на одной мультиклетке. Так как количество ядер сильно отличается в разных процессорах, то, для чистоты эксперимента, рассмотрим показатели в расчёте на мегагерц.
Сравнительная таблица показателей Whetstone:
| Процессор | MultiClet R1 | MultiClet S1 | Core i7 4820K | ARM v8-A53 |
|---|---|---|---|---|
| Частота, MHz | 100 | 1600 | 3900 | 1300 |
| MWIPS / MHz | 0.311 | 0.343 | 0.887 | 0.642 |
| MFLOPS1 / MHz | 0.157 | 0.156 | 0.341 | 0.268 |
| MFLOPS2 / MHz | 0.153 | 0.111 | 0.308 | 0.241 |
| MFLOPS3 / MHz | 0.029 | 0.124 | 0.167 | 0.239 |
| COS MOPS / MHz | 0.018 | 0.008 | 0.023 | 0.028 |
| EXP MOPS / MHz | 0.008 | 0.005 | 0.014 | 0.004 |
| FIXPT MOPS / MHz | 0.714 | 0.116 | 0.998 | 1.197 |
| IF MOPS / MHz | 0.081 | 0.196 | 1.504 | 1.436 |
| EQUAL MOPS / MHz | 0.143 | 0.149 | 0.251 | 0.439 |
Whetstone содержит гораздо больше непосредственно вычислительных операций, чем CoreMark (что очень заметно, глядя на код ниже), поэтому здесь важно помнить: количество блоков ALU с плавающей точкой сокращено в два раза. Однако, скорость вычислений почти не пострадала, в сравнении с R1.
Некоторые модули очень хорошо ложатся на мультиклеточную архитектуру. Например, модуль 2 считает в цикле множество значений, и благодаря полной поддержке чисел с плавающей точкой двойной точности как процессором, так и компилятором, после компиляции получаются большие и красивые параграфы, где по настоящему раскрываются вычислительные возможности мультиклеточной архитектуры:
pa:
SR4 := loadu_q [#SP + 16]
SR5 := loadu_q [#SP + 8]
SR6 := loadu_l [#SP + 4]
SR7 := loadu_l [#SP]
setjf_l @0, @SR7
SR8 := add_l @SR6, 0x8
SR9 := add_l @SR6, 0x10
SR10 := add_l @SR6, 0x18
SR11 := loadu_q [@SR6]
SR12 := loadu_q [@SR8]
SR13 := loadu_q [@SR9]
SR14 := loadu_q [@SR10]
SR15 := add_d @SR11, @SR12
SR11 := add_d @SR15, @SR13
SR15 := sub_d @SR11, @SR14
SR11 := mul_d @SR15, @SR5
SR15 := add_d @SR12, @SR11
SR12 := sub_d @SR15, @SR13
SR15 := add_d @SR14, @SR12
SR12 := mul_d @SR15, @SR5
SR15 := sub_d @SR11, @SR12
SR16 := sub_d @SR12, @SR11
SR17 := add_d @SR11, @SR12
SR11 := add_d @SR13, @SR15
SR13 := add_d @SR14, @SR11
SR11 := mul_d @SR13, @SR5
SR13 := add_d @SR16, @SR11
SR15 := add_d @SR17, @SR11
SR16 := add_d @SR14, @SR13
SR13 := div_d @SR16, @SR4
SR14 := sub_d @SR15, @SR13
SR15 := mul_d @SR14, @SR5
SR14 := add_d @SR12, @SR15
SR12 := sub_d @SR14, @SR11
SR14 := add_d @SR13, @SR12
SR12 := mul_d @SR14, @SR5
SR14 := sub_d @SR15, @SR12
SR16 := sub_d @SR12, @SR15
SR17 := add_d @SR15, @SR12
SR15 := add_d @SR11, @SR14
SR11 := add_d @SR13, @SR15
SR14 := mul_d @SR11, @SR5
SR11 := add_d @SR16, @SR14
SR15 := add_d @SR17, @SR14
SR16 := add_d @SR13, @SR11
SR11 := div_d @SR16, @SR4
SR13 := sub_d @SR15, @SR11
SR15 := mul_d @SR13, @SR5
SR13 := add_d @SR12, @SR15
SR12 := sub_d @SR13, @SR14
SR13 := add_d @SR11, @SR12
SR12 := mul_d @SR13, @SR5
SR13 := sub_d @SR15, @SR12
SR16 := sub_d @SR12, @SR15
SR17 := add_d @SR15, @SR12
SR15 := add_d @SR14, @SR13
SR13 := add_d @SR11, @SR15
SR14 := mul_d @SR13, @SR5
SR13 := add_d @SR16, @SR14
SR15 := add_d @SR17, @SR14
SR16 := add_d @SR11, @SR13
SR11 := div_d @SR16, @SR4
SR13 := sub_d @SR15, @SR11
SR4 := loadu_q @SR4
SR5 := loadu_q @SR5
SR6 := loadu_q @SR6
SR7 := loadu_q @SR7
SR15 := mul_d @SR13, @SR5
SR8 := loadu_q @SR8
SR9 := loadu_q @SR9
SR10 := loadu_q @SR10
SR13 := add_d @SR12, @SR15
SR12 := sub_d @SR13, @SR14
SR13 := add_d @SR11, @SR12
SR12 := mul_d @SR13, @SR5
SR13 := sub_d @SR15, @SR12
SR16 := sub_d @SR12, @SR15
SR17 := add_d @SR15, @SR12
SR15 := add_d @SR14, @SR13
SR13 := add_d @SR11, @SR15
SR14 := mul_d @SR13, @SR5
SR13 := add_d @SR16, @SR14
SR15 := add_d @SR17, @SR14
SR16 := add_d @SR11, @SR13
SR11 := div_d @SR16, @SR4
SR13 := sub_d @SR15, @SR11
SR15 := mul_d @SR13, @SR5
SR13 := add_d @SR12, @SR15
SR12 := sub_d @SR13, @SR14
SR13 := add_d @SR11, @SR12
SR12 := mul_d @SR13, @SR5
SR13 := sub_d @SR15, @SR12
SR16 := sub_d @SR12, @SR15
SR17 := add_d @SR15, @SR12
SR15 := add_d @SR14, @SR13
SR13 := add_d @SR11, @SR15
SR14 := mul_d @SR13, @SR5
SR13 := add_d @SR16, @SR14
SR15 := add_d @SR17, @SR14
SR16 := add_d @SR11, @SR13
SR11 := div_d @SR16, @SR4
SR13 := sub_d @SR15, @SR11
SR15 := mul_d @SR13, @SR5
SR13 := add_d @SR12, @SR15
SR12 := sub_d @SR13, @SR14
SR13 := add_d @SR11, @SR12
SR12 := mul_d @SR13, @SR5
SR13 := sub_d @SR15, @SR12
SR16 := sub_d @SR12, @SR15
SR17 := add_d @SR14, @SR13
SR13 := add_d @SR11, @SR17
SR14 := mul_d @SR13, @SR5
SR5 := add_d @SR16, @SR14
SR13 := add_d @SR11, @SR5
SR5 := div_d @SR13, @SR4
wr_q @SR15, @SR6
wr_q @SR12, @SR8
wr_q @SR14, @SR9
wr_q @SR5, @SR10
complete
popcnt
Для отражения характеристик самой архитектуры (без зависимости от компилятора) измерим что-нибудь, написанное на ассемблере с учетом всех особенностей архитектуры. Например, подсчет единичных бит в 512-ти битном числе (popcnt). Для очевидности будем брать результаты одной мультиклетки, чтобы их можно было сравнить с R1.
Сравнительная таблица, количество тактов на один цикл расчёта 32-х бит:
| Алгоритм | Multiclet R1 | Multiclet S1 (одна мультиклетка) |
|---|---|---|
| BitHacks | 5.0 | 2.625 |
Здесь были использованы новые обновленные векторные инструкции, что позволило сократить количество инструкций в два раза, по сравнению с таким же алгоритмом, реализованным на ассемблере R1. Скорость работы, соответственно, увеличилась в почти в 2 раза.
bithacks:
b0 := patch_q 0x1, 0x1
v0 := loadu_q [v]
v1 := loadu_q [v+8]
v2 := loadu_q [v+16]
v3 := loadu_q [v+24]
v4 := loadu_q [v+32]
v5 := loadu_q [v+40]
v6 := loadu_q [v+48]
v7 := loadu_q [v+56]
b1 := patch_q 0x55555555, 0x55555555
i00 := slr_pl @v0, @b0
i01 := slr_pl @v1, @b0
i02 := slr_pl @v2, @b0
i03 := slr_pl @v3, @b0
i04 := slr_pl @v4, @b0
i05 := slr_pl @v5, @b0
i06 := slr_pl @v6, @b0
i07 := slr_pl @v7, @b0
b2 := patch_q 0x33333333, 0x33333333
i10 := and_q @i00, @b1
i11 := and_q @i01, @b1
i12 := and_q @i02, @b1
i13 := and_q @i03, @b1
i14 := and_q @i04, @b1
i15 := and_q @i05, @b1
i16 := and_q @i06, @b1
i17 := and_q @i07, @b1
b3 := patch_q 0x2, 0x2
i20 := sub_pl @v0, @i10
i21 := sub_pl @v1, @i11
i22 := sub_pl @v2, @i12
i23 := sub_pl @v3, @i13
i24 := sub_pl @v4, @i14
i25 := sub_pl @v5, @i15
i26 := sub_pl @v6, @i16
i27 := sub_pl @v7, @i17
i30 := and_q @i20, @b2
i31 := and_q @i21, @b2
i32 := and_q @i22, @b2
i33 := and_q @i23, @b2
i34 := and_q @i24, @b2
i35 := and_q @i25, @b2
i36 := and_q @i26, @b2
i37 := and_q @i27, @b2
i40 := slr_pl @i20, @b3
i41 := slr_pl @i21, @b3
i42 := slr_pl @i22, @b3
i43 := slr_pl @i23, @b3
i44 := slr_pl @i24, @b3
i45 := slr_pl @i25, @b3
i46 := slr_pl @i26, @b3
i47 := slr_pl @i27, @b3
b4 := patch_q 0x4, 0x4
i50 := and_q @i40, @b2
i51 := and_q @i41, @b2
i52 := and_q @i42, @b2
i53 := and_q @i43, @b2
i54 := and_q @i44, @b2
i55 := and_q @i45, @b2
i56 := and_q @i46, @b2
i57 := and_q @i47, @b2
i60 := add_pl @i50, @i30
i61 := add_pl @i51, @i31
i62 := add_pl @i52, @i32
i63 := add_pl @i53, @i33
i64 := add_pl @i54, @i34
i65 := add_pl @i55, @i35
i66 := add_pl @i56, @i36
i67 := add_pl @i57, @i37
b5 := patch_q 0xf0f0f0f, 0xf0f0f0f
i70 := slr_pl @i60, @b4
i71 := slr_pl @i61, @b4
i72 := slr_pl @i62, @b4
i73 := slr_pl @i63, @b4
i74 := slr_pl @i64, @b4
i75 := slr_pl @i65, @b4
i76 := slr_pl @i66, @b4
i77 := slr_pl @i67, @b4
b6 := patch_q 0x1010101, 0x1010101
i80 := add_pl @i70, @i60
i81 := add_pl @i71, @i61
i82 := add_pl @i72, @i62
i83 := add_pl @i73, @i63
i84 := add_pl @i74, @i64
i85 := add_pl @i75, @i65
i86 := add_pl @i76, @i66
i87 := add_pl @i77, @i67
b7 := patch_q 0x18, 0x18
i90 := and_q @i80, @b5
i91 := and_q @i81, @b5
i92 := and_q @i82, @b5
i93 := and_q @i83, @b5
i94 := and_q @i84, @b5
i95 := and_q @i85, @b5
i96 := and_q @i86, @b5
i97 := and_q @i87, @b5
iA0 := mul_pl @i90, @b6
iA1 := mul_pl @i91, @b6
iA2 := mul_pl @i92, @b6
iA3 := mul_pl @i93, @b6
iA4 := mul_pl @i94, @b6
iA5 := mul_pl @i95, @b6
iA6 := mul_pl @i96, @b6
iA7 := mul_pl @i97, @b6
iB0 := slr_pl @iA0, @b7
iB1 := slr_pl @iA1, @b7
iB2 := slr_pl @iA2, @b7
iB3 := slr_pl @iA3, @b7
iB4 := slr_pl @iA4, @b7
iB5 := slr_pl @iA5, @b7
iB6 := slr_pl @iA6, @b7
iB7 := slr_pl @iA7, @b7
wr_q @iB0, c
wr_q @iB1, c+8
wr_q @iB2, c+16
wr_q @iB3, c+24
wr_q @iB4, c+32
wr_q @iB5, c+40
wr_q @iB6, c+48
wr_q @iB7, c+56
complete
Ethereum
Бенчмарки это, конечно, хорошо, но у нас есть конкретная задача: сделать ускоритель вычислений, и неплохо было бы знать, как он справляется на реальных задачах. Современные криптовалюты как нельзя лучше подходят для такой проверки, потому что алгоритмы майнинга запускаются на множестве разных устройств и поэтому могут служить в качестве бенчмарка для сравнения. Начали с Ethereum и алгоритма Ethash, который выполняется непосредственно на майнящем устройстве.
Выбор Ethereum был обусловлен следующими соображениями. Как известно, алгоритмы типа Bitcoin весьма эффективно реализуются специализированными ASIC чипами, поэтому использование процессоров или видеокарт для майнинга Bitcoin и его клонов становится экономически невыгодным из-за низкой производительности и высокого энергопотребления. Сообщество майнеров, в попытке уйти от этой ситуации, разрабатывает криптовалюты на других алгоритмических принципах, делая упор на разработке алгоритмов, которые используют для майнинга процессоры общего назначения или видеокарты. Эта тенденция, видимо, сохранится и в будущем. Ethereum является наиболее известной криптовалютой, основанной на этом подходе. Основным инструментом для майнинга Ethereum являются видеокарты, которые по эффективности (hashrate / TDP) существенно (в несколько раз) опережают процессоры общего назначения.
Ethash – это так называемым memory bound алгоритм, т.е. время его вычисления ограничено в первую очередь количеством и скоростью памяти, а не скоростью самих вычислений. Сейчас для майнинга Ethereum как нельзя лучше подходят видеокарты, но их возможность параллельно исполнять множество операций не сильно помогает, и они по прежнему упираются в скорость оперативной памяти, что наглядно продемонстрировано в этой статье. Оттуда же можно взять картинку, иллюстрирующую работу алгоритма, чтобы пояснить, почему так получается.
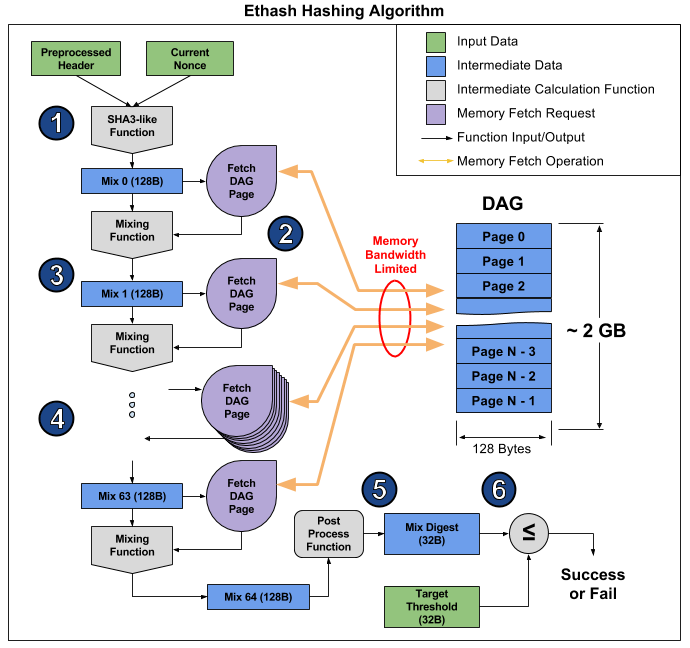
Статья разбивает алгоритм на 6 пунктов, но можно выделить 3 этапа для еще большей очевидности:
- Начало: SHA-3 (512) для вычисления изначального 128-байтового Mix 0 (пункт 1)
- 64-кратный пересчет массива Mix путём считывания следующих 128 байт и смешивания их с предыдущими через mixing function, итого 8 килобайт (пункты 2-4)
- Финализация и проверка результата
Считывание случайных 128 байт из оперативной памяти занимает куда больше времени, чем кажется. Если взять видеокарту MSI RX 470, у которой 2048 вычислительных устройств и максимальная пропускная способность памяти 211.2 ГБ/с, то для того чтобы снабдить каждое устройство потребуется 1 / (211.2 ГБ / (128 б * 2048)) = 1241 нс, или примерно 1496 тактов при заданной частоте. Учитывая размер mixing function, можно предположить, что на считывание памяти у видеокарты уходит в разы больше времени, чем на пересчёт полученной информации. В результате, этап 2 алгоритма занимает очень много времени, гораздо больше, чем этапы 1 и 3, которые в итоге слабо влияют на производительность, несмотря на то, что они содержат больше вычислений (в основном, в SHA-3). Можно просто посмотреть на хэшрейт этой видеокарты: 26.375 мегахэшей/с теоретического (ограниченного только по пропускной способности памяти) против 24 мегахэшей/с фактического, то есть этапы 1 и 3 занимают всего 10% времени.
На S1 все 16 мультиклеток могут работать параллельно и над разным кодом. К тому же, будет установлена двухканальная оперативная память, по одному каналу на 8 мультиклеток. На этапе 2 алгоритма Ethash план у нас таков: одна мультиклетка читает 128 байт из памяти и начинает их пересчет, затем следующая читает память и выполняет пересчет и так до 8й, т.е. у одной мультиклетки, после прочитывания 128 байт памяти, есть 7 * [время считывания 128 байт] на пересчет массива. Предполагается, что такое считывание будет занимать 16 тактов, т.е. 112 тактов дано на пересчет. Вычисление mixing function занимает у нас примерно столько же тактов, так что S1 близок к идеальному соотношению пропускной способности памяти к производительности самого процессора. Так как времени на второй этап впустую не тратится, то нужно максимально оптимизировать остальные части алгоритма, потому что тогда они действительно влияют на производительность.
Для оценки скорости вычисления SHA-3 (Keccak) была разработана и отработана программа на языке C, на основе которой в настоящее время создается ее оптимальная версия на ассемблере. Оценочное программирования показывает, что одна мультиклетка выполняет вычисление SHA-3 (Keccak) за 1550 тактов. Следовательно, общее время вычисления одного хэша одной мультиклеткой составит 1550 + 64 * (16 + 112) = 9742 такта. При частоте 1.6 ГГц и 16 параллельно работающих мультиклеток хэшрейт процессора составит 2.6 MHash/s.
| Ускоритель | MultiClet S1 | NVIDIA GeForce GTX 980 Ti | Radeon RX 470 | Radeon RX Vega 64 | NVIDIA GeForce GTX 1060 | NVIDIA GeForce GTX 1080 Ti |
|---|---|---|---|---|---|---|
| Цена | $650 | $180 | $500 | $300 | $700 | |
| Хэшрейт | 2.6 MHash/s | 21.6 MHash/s | 25.8 MHash/s | 43.5 MHash/s | 25 MHash/s | 55 MHash/s |
| TDP | 6 W | 250 W | 120 W | 295 W | 120 W | 250 W |
| Хэшрейт / TDP | 0.43 | 0.09 | 0.22 | 0.15 | 0.22 | 0.21 |
| Техпроцесс | 28 нм | 28 нм | 14 нм | 14 нм | 16 нм | 16 нм |
При использовании MultiClet S1 в качестве инструмента для майнинга, на платы реально может быть установлено 20 и более процессоров. В этом случае, хэшрейт такой платы будет равен либо превышать хэшрейты существующих видеокарт, при этом энергопотребление платы с S1 будет в два раза меньше, даже чем у видеокарт с топонормами 16 и 14 нм.
В завершение нужно сказать, что основной задачей сейчас является изготовление многопроцессорной платы для мультиклеточного майнера криптовалют и суперкомпьютинга. Конкурентоспособность планируется достичь за счёт маленького энергопотребления и архитектуры, хорошо подходящей для произвольных вычислений.
Процессор ещё в разработке, но вы уже можете начать программировать на ассемблере, а также оценить текущую версию компилятора. Уже есть минимальный SDK, содержащий ассемблер, линкер, компилятор и функциональную модель, на которой как раз и можно запустить и потестировать ваши программы.
Комментариев нет:
Отправить комментарий