Введение
Реверс-инжиниринг незнакомого файла данных можно описать как процесс постепенного понимания. Он во многом напоминает научный метод, только применённый к созданным человеком абстрактным объектам, а не к миру природы. Мы начинаем со сбора данных, а затем используем эту информацию для выдвижения одной или нескольких гипотез. Проверяем гипотезы и применяем результаты этих проверок для их уточнения. При необходимости повторяем процесс.
Развитие навыков реверс-инжиниринга — в основном вопрос практики. Накапливая опыт, вы выстраиваете интуитивное понимание того, что нужно исследовать в первую очередь, какие паттерны необходимо искать, и какие инструменты удобнее использовать.
В этой статье я подробно расскажу о процессе обратной разработки файлов данных из старой компьютерной игры, чтобы продемонстрировать, как это делается.
Небольшая предыстория
Всё это началось, когда я пытался воссоздать игру Chip's Challenge на Linux.
Изначально Chip's Challenge была выпущена в 1989 году для ныне забытой портативной консоли Atari Lynx. Для того времени Atari Lynx была впечатляющей машиной, но она вышла в одно время с Nintendo Game Boy, которая в конце концов захватила рынок.
Chip's Challenge — это игра-головоломка с видом сверху и тайловой картой. Как и в большинстве таких игр, цель каждого уровня заключается в том, чтобы добраться до выхода. В большей части уровней выход охраняется разъёмом для чипа, который можно миновать, только собрав определённое количество компьютерных чипов.

Видео: Atari Lynx в действии, прохождение первого уровня.
Новая игра начинается с первого уровня под названием «LESSON 1». Кроме чипов и разъёма для чипа, на нём появляются ключи и двери. На других уровнях возникают такие препятствия, как ловушки, бомбы, вода и существа, которые (чаще всего) движутся по предсказуемым маршрутам. Широкий набор объектов и устройств позволяет создавать множество загадок и ограничений по времени. Для завершения игры нужно пройти более 140 уровней.
Хотя Lynx в конце концов потерпела неудачу, Chip's Challenge оказалась достаточно популярной и была портирована на множество других платформ, со временем появившись и на Microsoft Windows, где получила широкое распространение. Вокруг игры образовалась небольшая, но преданная база фанатов, и со временем был написан редактор уровней, позволявший игрокам создавать бесчисленные уровни.
И с этого начинается моя история. Я решил, что хочу создать версию базового движка игры с открытым исходным кодом, чтобы можно было играть в Chip's Challenge в Linux и в Windows, и упростить запуск всех уровней, созданных фанатами.
Существование редактора уровней оказалось для меня чудом, потому что я мог исследовать скрытые особенности логики игры, создавая собственные уровни и проводя тесты. К сожалению, для оригинальной игры на Lynx редактора уровней не было, он появился только в более известном порте под Windows.
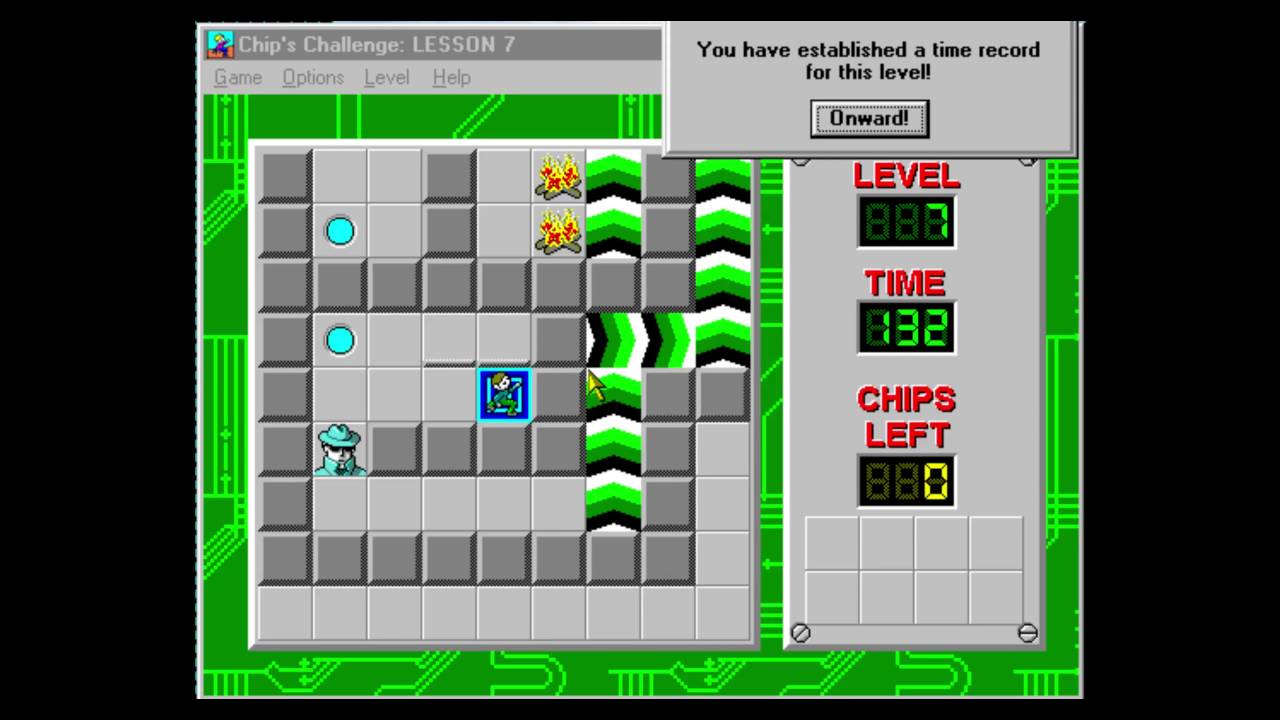
Порт под Windows создавался не разработчиками оригинала, поэтому в нём появилось множество изменений логики игры (и не все они были намеренными). Когда я начал писать свой движок, я хотел воссоздать в нём и логику игры оригинала на Lynx, и более известной версии под Windows. Но отсутствие редактора уровней на Lynx серьёзно ограничило мои возможности по подробному исследованию оригинальной игры. Порт под Windows имел преимущество: уровни сохранялись в отдельный файл данных, что упрощало его обнаружение и реверс-инжиниринг. Игра под Lynx распространялась на ROM-картриджах, содержавших спрайтовые изображения, звуковые эффекты и машинный код, а также данные уровней, которые выполнялись все вместе. Нет никаких намёков о том, где находятся данные в этом 128-килобайтном дампе ROM, или как они выглядят, а без этих знаний я никак не мог создать редактор уровней для версии на Lynx.
Однажды в процессе неторопливых исследований я наткнулся на копию порта Chip's Challenge под MS-DOS. Как и в большинстве ранних портов игры, его логика была ближе к оригиналу, чем в версии под Windows. Когда я посмотрел на данные программы, чтобы узнать, как они хранятся, я с удивлением обнаружил, что данные уровней были выделены в отдельный каталог, а каждый уровень хранился в своём файле. Имея так удобно отделённые данные уровней, я предположил, что будет не слишком сложно выполнить реверс-инжиниринг файлов данных уровней. А это позволит написать редактор уровней для версии игры под MS-DOS. Я решил, что это интересная возможность.
Но затем другой участник сообщества Chip's Challenge предупредил меня об интересном факте. Содержимое файлов уровней для MS-DOS оказалось побайтным дампом ROM Lynx. Это означало, что если я смогу декодировать файлы MS-DOS, то у меня получится затем использовать это знание для чтения и изменения уровней внутри дампа ROM Lynx. Тогда можно будет создать редактор уровней непосредственно для оригинальной игры на Lynx.
Внезапно моим основным приоритетом стал реверс-инжиниринг файлов уровней для MS-DOS.
Файлы данных
Вот ссылка на tarball каталога, содержащего все файлы данных. Я даю её на случай, если вы захотите повторять за мной все шаги, описанные в этой статье, или попытаетесь самостоятельно декодировать файлы данных.
Законно ли это? Хороший вопрос. Поскольку эти файлы являются только небольшой частью программы для MS-DOS, и сами по себе они бесполезны, и поскольку я выкладываю их только в образовательных целях, то полагаю, что это подпадает под требованиях добросовестного использования (fair use). Надеюсь, со мной согласятся все заинтересованные стороны. (Если же я всё-таки получу от юристов письмо с угрозами, то могу изменить статью так, чтобы изложить файлы данных в забавном ключе, а затем заявить, что это пародия.)
Предварительные требования
Я буду считать, что вы знаете шестнадцатеричное исчисление, пусть даже и не владеете декодированием шестнадцатеричных значений, а также что вы немного знакомы с командной оболочкой (shell) Unix. Показанная в этой статье сессия оболочки выполняется на стандартной системе Linux, но почти используемые команды являются распространёнными утилитами Unix, и широко распространены на других Unix-подобных системах.
Первый взгляд
Вот листинг каталога, содержащего файлы данных из порта под MS-DOS:
$ ls levels all_full.pak cake_wal.pak eeny_min.pak iceberg.pak lesson_5.pak mulligan.pak playtime.pak southpol.pak totally_.pak alphabet.pak castle_m.pak elementa.pak ice_cube.pak lesson_6.pak nice_day.pak potpourr.pak special.pak traffic_.pak amsterda.pak catacomb.pak fireflie.pak icedeath.pak lesson_7.pak nightmar.pak problems.pak spirals.pak trinity.pak apartmen.pak cellbloc.pak firetrap.pak icehouse.pak lesson_8.pak now_you_.pak refracti.pak spooks.pak trust_me.pak arcticfl.pak chchchip.pak floorgas.pak invincib.pak lobster_.pak nuts_and.pak reverse_.pak steam.pak undergro.pak balls_o_.pak chiller.pak forced_e.pak i.pak lock_blo.pak on_the_r.pak rink.pak stripes.pak up_the_b.pak beware_o.pak chipmine.pak force_fi.pak i_slide.pak loop_aro.pak oorto_ge.pak roadsign.pak suicide.pak vanishin.pak blink.pak citybloc.pak force_sq.pak jailer.pak memory.pak open_que.pak sampler.pak telebloc.pak victim.pak blobdanc.pak colony.pak fortune_.pak jumping_.pak metastab.pak oversea_.pak scavenge.pak telenet.pak vortex.pak blobnet.pak corridor.pak four_ple.pak kablam.pak mind_blo.pak pain.pak scoundre.pak t_fair.pak wars.pak block_fa.pak cypher.pak four_squ.pak knot.pak mishmesh.pak paranoia.pak seeing_s.pak the_last.pak writers_.pak block_ii.pak deceptio.pak glut.pak ladder.pak miss_dir.pak partial_.pak short_ci.pak the_mars.pak yorkhous.pak block_n_.pak deepfree.pak goldkey.pak lemmings.pak mixed_nu.pak pentagra.pak shrinkin.pak the_pris.pak block_ou.pak digdirt.pak go_with_.pak lesson_1.pak mix_up.pak perfect_.pak skelzie.pak three_do.pak block.pak digger.pak grail.pak lesson_2.pak monster_.pak pier_sev.pak slide_st.pak time_lap.pak bounce_c.pak doublema.pak hidden_d.pak lesson_3.pak morton.pak ping_pon.pak slo_mo.pak torturec.pak brushfir.pak drawn_an.pak hunt.pak lesson_4.pak mugger_s.pak playhous.pak socialis.pak tossed_s.pak
Как видите, все файлы заканчиваются на
.pak. .pak является стандартным разрешением для файла данных приложений, и это, к сожалению, не даёт нам никакой информации о его внутренней структуре. Названия файлов — это первые восемь символов названия уровня, за некоторыми исключениями. (Например, в названиях файлов уровней «BLOCK BUSTER» и «BLOCK BUSTER II» опущено слово «buster», чтобы они не совпадали.)
$ ls levels | wc
17 148 1974
В каталоге находится 148 файлов данных, и в игре на самом деле ровно 148 уровней, так что тут всё совпадает.
Теперь давайте изучим, что же представляют собой эти файлы. xxd — это стандартная утилита для дампа шестнадцатеричных данных (hexdump). Давайте посмотрим, как выглядит внутри «LESSON 1».
$ xxd levels/lesson_1.pak 00000000: 1100 cb00 0200 0004 0202 0504 0407 0505 ................ 00000010: 0807 0709 0001 0a01 010b 0808 0d0a 0a11 ................ 00000020: 0023 1509 0718 0200 2209 0d26 0911 270b .#......"..&..'. 00000030: 0b28 0705 291e 0127 2705 020d 0122 0704 .(..)..''....".. 00000040: 0902 090a 0215 0426 0925 0111 1502 221d .......&.%....". 00000050: 0124 011d 0d01 0709 0020 001b 0400 1a00 .$....... ...... 00000060: 2015 2609 1f00 3300 2911 1522 2302 110d .&...3.).."#... 00000070: 0107 2609 1f18 2911 1509 181a 0223 021b ..&...)......#.. 00000080: 0215 2201 1c01 1c0d 0a07 0409 0201 0201 .."............. 00000090: 2826 0123 1505 0902 0121 1505 220a 2727 (&.#.....!..".'' 000000a0: 0b05 0400 060b 0828 0418 780b 0828 0418 .......(..x..(.. 000000b0: 700b 0828 0418 6400 1710 1e1e 1a19 0103 p..(..d......... 000000c0: 000e 1a17 1710 0e1f 010e 1314 1b29 1f1a .............).. 000000d0: 0012 101f 011b 0c1e 1f01 1f13 1001 0e13 ................ 000000e0: 141b 001e 1a0e 1610 1f2d 0020 1e10 0116 .........-. .... 000000f0: 1024 291f 1a01 1a1b 1019 000f 1a1a 1d1e .$)............. 00000100: 2d02
Что такое утилита для создания hexdump? Шестнадцатеричный дамп — это стандартный способ отображения точных байтов двоичного файла. Большинство байтовых значений нельзя связать с печатными символами ASCII, или они имеют непонятный внешний вид (например символ табуляции). В шестнадцатеричном дампе отдельные байты выводятся в виде численных значений. Значения отображаются в шестнадцатеричном виде, отсюда и название. В показанном выше примере в одной строке вывода отображается 16 байт. Самый левый столбец показывает позицию строки в файле, тоже в шестнадцатеричном виде, поэтому в каждой строке число увеличивается на 16. Байты отображаются в восемь столбцов, и в каждом столбце отображается по два байта. Справа в hexdump показывается, как бы выглядели байты при отображении символами, только все непечатаемые значения ASCII заменены точками. Это упрощает нахождение строк, которые могут быть встроены в двоичный файл.
Очевидно, что реверс-инжиниринг этих файлов не будет сводиться к обычному просмотру содержимого и изучению того, что там видно. Пока здесь нет ничего не говорит нам о том, какие функции выполняют данные.
Что мы ожидаем увидеть?
Давайте сделаем шаг назад и проясним ситуацию: какие конкретно данные мы ожидаем найти в этих файлах данных?
Самое очевидное — это некая «карта» уровня: данные, обозначающие позиции стен и дверей, а также всего остального, что делает уровень уникальным.

(К счастью для нас, фанаты игры проделали кропотливую работу и собрали полные карты для всех 148 уровней, поэтому мы можем использовать их, чтобы знать, что должно находиться на каждой карте.)
В дополнение к карте у каждого уровня должно быть несколько других атрибутов. Например, можно заметить, что у каждого уровня есть название, например «LESSON 1», «PERFECT MATCH», «DRAWN AND QUARTERED», и так далее. У разных уровней также есть разные ограничения по времени, поэтому можно предположить, что эта информация тоже содержится в данных. Кроме того, на каждом уровне есть собственное число собираемых чипов. (Мы могли бы предположить, что это число просто соответствует количеству чипов на уровне, но оказывается, что на некоторых уровнях содержится больше чипов, чем нужно для открытия разъёма чипов. Хотя бы для этих уровней минимальное количество должно указываться в явной форме.)
Ещё один фрагмент данных, который мы ожидаем найти в данных уровня — это текст подсказок. На некоторых уровнях есть «кнопка подсказки» — лежащий на земле большой вопросительный знак. Когда Чип встаёт на него, показывается текст подсказки. Кнопка подсказки есть примерно на 20 уровнях.
Наконец, у каждого уровня есть пароль — последовательность из четырёх букв, позволяющая игроку продолжить игру с этого уровня. (Этот пароль необходим, потому что в Lynx нет хранилища данных. Сохранять на консоли игры было нельзя, поэтому продолжать игру после включения консоли можно было с помощью паролей.)
Итак, вот наш список нужных данных:
- Карта уровня
- Название уровня
- Пароль уровня
- Ограничение времени
- Количество чипов
- Текст подсказки
Давайте примерно оценим общий размер данных. Проще всего определить ограничение по времени и количество чипов. Оба эти параметра могут иметь значения в интервале от 0 до 999, поэтому они скорее всего хранятся в виде целочисленных значений общим размером 4 байта. Пароль всегда состоит из четырёх букв, поэтому скорее всего хранится как ещё четыре байта, то есть всего 8 байт. Длина названий уровней варьируется от четырёх до девятнадцати символов. Если мы предположим, что нужен ещё один байт для завершения строки, то это двадцать байт, то есть промежуточный итог составляет 28 байт. Самый длинный текст подсказки имеет размер более 80 байт; если мы округлим это значение до 90, то в сумме получим 118 байт.
А что насчёт схемы уровня? Большинство уровней имеет размер 32 × 32 тайлов. Уровней большего размера не существует. Некоторые уровни меньше, но будет логично предположить, что они просто встроены в карту размером 32 × 32. Если предположить, что на один тайл карте требуется один байт, то для полной схемы нужно 1024 байта. То есть в целом мы получаем приблизительную оценку в 1142 байта на каждый уровень. Разумеется, это всего лишь грубая первоначальная прикидка. Вполне возможно, что некоторые из этих элементов хранятся иначе, или вообще не хранятся внутри файлов уровней. Или в них могут находиться другие данные, которые мы не заметили или не знаем о них. Но пока мы заложили неплохую основу.
Определившись с тем, что мы ожидаем увидеть в файлах данных, давайте вернёмся к изучению того, что же на самом деле в них содержится.
Что там есть и чего нет
Хотя на первый взгляд файл данных выглядит совершенно непонятно, в нём всё равно можно заметить пару моментов. Во-первых, это то, чего мы не видим. Например, мы не видим названия уровня или текста подсказок. Можно понять, что это не совпадение, изучив и другие файлы:
$ strings levels/* | less :!!;# &>''::4# .,,! -54"; /&67 !)60 <171 *(0* 82>'=/ 8><171&& 9>#2')( , )9 0hX `@PX )""* 24**5 ;))< B777:..22C1 E,,F -GDED EGFF16G;;H< IECJ 9K444 =MBBB>>N9"O"9P3?Q lines 1-24/1544 (more)
Здесь ничего не видно, кроме произвольных фрагментов ASCII-мусора.
Предположительно, где-то в этих файлах есть названия уровней и подсказки, но они или хранятся не в ASCII, или претерпели некую трансформацию (например, из-за сжатия).
Стоит также заметить следующее: файл едва дотягивает по размеру до 256 байт. Это довольно мало, учитывая, что изначально мы оценили его размер более чем в 1140 байт.
Опция -S сортирует файлы по убыванию размера.
$ ls -lS levels | head total 592 -rw-r--r-- 1 breadbox breadbox 680 Jun 23 2015 mulligan.pak -rw-r--r-- 1 breadbox breadbox 675 Jun 23 2015 shrinkin.pak -rw-r--r-- 1 breadbox breadbox 671 Jun 23 2015 balls_o_.pak -rw-r--r-- 1 breadbox breadbox 648 Jun 23 2015 cake_wal.pak -rw-r--r-- 1 breadbox breadbox 647 Jun 23 2015 citybloc.pak -rw-r--r-- 1 breadbox breadbox 639 Jun 23 2015 four_ple.pak -rw-r--r-- 1 breadbox breadbox 636 Jun 23 2015 trust_me.pak -rw-r--r-- 1 breadbox breadbox 625 Jun 23 2015 block_n_.pak -rw-r--r-- 1 breadbox breadbox 622 Jun 23 2015 mix_up.pak
Самый большой файл занимает всего 680 байт, и это не очень много. А каким будет самый маленький?
Опция -r сообщает ls, что нужно обратить порядок.
$ ls -lSr levels | head total 592 -rw-r--r-- 1 breadbox breadbox 206 Jun 23 2015 kablam.pak -rw-r--r-- 1 breadbox breadbox 214 Jun 23 2015 fortune_.pak -rw-r--r-- 1 breadbox breadbox 219 Jun 23 2015 digdirt.pak -rw-r--r-- 1 breadbox breadbox 226 Jun 23 2015 lesson_2.pak -rw-r--r-- 1 breadbox breadbox 229 Jun 23 2015 lesson_8.pak -rw-r--r-- 1 breadbox breadbox 237 Jun 23 2015 partial_.pak -rw-r--r-- 1 breadbox breadbox 239 Jun 23 2015 knot.pak -rw-r--r-- 1 breadbox breadbox 247 Jun 23 2015 cellbloc.pak -rw-r--r-- 1 breadbox breadbox 248 Jun 23 2015 torturec.pak
Самый мелкий файл занимает всего 206 байт, что в три с лишним раза меньше самого большого. Это довольно широкий интервал с учётом того, что мы ожидали примерно одинаковых размеров уровней.
В нашей первоначальной оценке мы предположили, что карте потребуется по одному байту на тайл, и всего 1024 байт. Если мы урежем эту оценку вдвое, то есть каждый тайл потребует всего 4 бита (или два тайла на байт), то карта всё равно будет занимать 512 байт. 512 меньше, чем 680, но по-прежнему больше, чем размер большинства уровней. И в любом случае — 4 бита обеспечит всего 16 различных значений, а в игре гораздо больше разных объектов.
То есть очевидно, что карты не хранятся в этих файлах в открытом виде. В них используется или более сложное кодирование, обеспечивающее более эффективное описание, и/или они каким-то образом сжаты. Например, в уровне «LESSON 1» мы можем увидеть, как пропущенные записи для «пустых» тайлов значительно уменьшат общий размер данных карты.
Мы можем посмотреть на карты самых больших файлов:

Карта уровня 57: STRANGE MAZE

Карта уровня 98: SHRINKING
а затем сравнить их с картами самых маленьких файлов:

Карта уровня 106: KABLAM
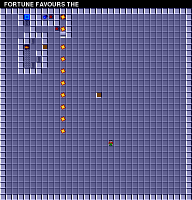
Карта уровня 112: FORTUNE FAVORS THE
Это сравнение поддерживают нашу идею о том, что маленькие файлы данных соответствуют более простым уровням, или содержат больше избыточности. Например, если данные сжаты каким-то кодированием длин серий (run-length encoding), это с лёгкостью может объяснить интервалы размеров разных файлов.
Если файлы и на самом деле зашифрованы, то нам, скорее всего, придётся расшифровать сжатие, прежде чем мы приступим к расшифровке данных карт.
Изучаем несколько файлов одновременно
Наше краткое изучение первого файла данных позволило нам сделать некоторые предположения, но не обнаружило ничего конкретного. В качестве следующего шага мы начнём исследовать паттерны нескольких файлов данных. Пока мы предположим, что во всех 148 файлах используется одинаковая схема упорядочивания для кодирования данных, поэтому поиск в этих файлов повторяющихся паттернов поможет нам приступить к работе.
Давайте начнём с самого начала тайлов. Верх файла скорее всего используется для хранения «метаданных», сообщающих нам о содержимом файла. Посмотрев только на первую строку шестнадцатеричного дампа, мы можем выполнить простое и быстрое сравнение первых 16 байтов и поискать в них выделяющиеся паттерны:
$ for f in levels/* ; do xxd $f | sed -n 1p ; done | less 00000000: 2300 dc01 0300 0004 0101 0a03 030b 2323 #.............## 00000000: 2d00 bf01 0300 0015 0101 2203 0329 2222 -........."..)"" 00000000: 2b00 a101 0301 0105 0000 0601 0207 0505 +............... 00000000: 1d00 d300 0200 0003 0101 0402 0205 0102 ................ 00000000: 2d00 7a01 0300 0006 1414 0701 0109 0303 -.z............. 00000000: 3100 0802 0200 0003 0101 0502 0206 1313 1............... 00000000: 1a00 b700 0200 0003 0100 0502 0206 0101 ................ 00000000: 1a00 0601 0300 0005 0001 0601 0107 0303 ................ 00000000: 2000 7a01 0200 0003 0202 0401 0105 0028 .z............( 00000000: 3a00 a400 0200 0003 2828 0428 0205 0303 :.......((.(.... 00000000: 2600 da00 0300 0004 0507 0901 010a 0303 &............... 00000000: 2400 f000 0300 0004 0303 0504 0407 0101 $............... 00000000: 2a00 ef01 0300 0005 0101 0614 0007 0303 *............... 00000000: 2c00 8c01 0300 0004 0303 0500 0107 0101 ,............... 00000000: 2a00 0001 0300 0004 0303 0501 0107 0404 *............... 00000000: 1b00 6d01 0200 0003 0101 0502 0206 0003 ..m............. 00000000: 1e00 1701 0200 0003 0202 0401 0105 0013 ................ 00000000: 3200 ee01 0f00 0015 0101 270f 0f29 1414 2.........'..).. 00000000: 2a00 5b01 0300 0005 0303 0601 0107 1414 *.[............. 00000000: 2c00 8a01 0200 0003 0202 0401 0105 0303 ,............... 00000000: 1d00 9c00 0216 1604 0000 0516 0107 0205 ................ 00000000: 2000 e100 0200 0003 0101 0402 0205 0303 ............... 00000000: 2000 2601 0300 0004 0303 0502 0207 0101 .&............. 00000000: 1f00 f600 0132 0403 0000 0532 3206 0404 .....2.....22... lines 1-24/148 (more)
Просмотрев этот дамп, можно заметить, что в каждом столбце возникают некие схожие значения.
Начав с первого байта, мы вскоре осознаём, что его значение находится в очень ограниченном интервале значений, в пределах шестнадцатеричных 10–40 (или примерно 20–60 в десятичном исчислении). Это довольно специфичная особенность.
Ещё интереснее то, что второй байт каждого файла всегда равен нулю, без исключений. Вероятно, второй байт не используется, или является заполнителем. Однако есть и другая вероятность — эти первые два байта вместе обозначают 16-битное значение, хранящееся в порядке little-endian.
Что такое little-endian? При сохранении численного значения, которое больше одного байта, нужно заранее выбрать порядок, в котором будут храниться байты. Если сначала вы сохраняете байт, представляющий меньшую часть числа, то это называется прямым порядком (little-endian); если вы сначала сохраняете байты, обозначающие бОльшую часть числа, то это обратный порядок (big-endian). Например, десятичные значения мы записываем в обратном порядке (big-endian): строка «42» означает «сорок два», а не «четыре и двадцать». Little-endian — это естественный порядок для многих семейств микропроцессоров, поэтому он обычно более популярен, за исключением сетевых протоколов, в которых обычно требуется big-endian.
Если мы продолжим анализ, то вскоре увидим, что третий байт в файле не похож на два предыдущих: его значение меняется в широком диапазоне. Однако четвёртый байт всегда равен
00, 01 или 02, и 01 встречается чаще всего. Это тоже намекает нам, что эти два байта составляют ещё одно 16-битное значение, находящееся примерно в интервале десятичных значений 0–700. Эту гипотезу можно подтвердить ещё и тем, что значение третьего байта обычно низко, если значение четвёртого равно 02, и обычно велико, если четвёртый байт равен 00.
Кстати, стоит заметить, что это частично причина того, что стандартно формат шестнадцатеричного дампа отображает байты по парам — так упрощается чтение последовательности 16-битных целочисленных чисел. Формат шестнадцатеричного дампа был стандартизован, когда в ходу были 16-битные компьютеры. Попробуйте заменить xxd на xxd -g1, чтобы полностью отключить группирование, и вы заметите, что распознавание пар байтов посередине строки требует больших усилий. Это простой пример того, как инструменты, используемые для изучения незнакомых данных, склоняют нас замечать определённые типы паттернов. Хорошо, что по умолчанию xxd выделяет этот паттерн, потому что он очень распространён (даже сегодня, когда повсюду используются 64-битные компьютеры). Но полезно и знать, как изменить эти параметры, если они не помогают.
Давайте продолжим визуальное исследование, и посмотрим, сохраняется ли этот паттерн из 16-битных целочисленных значений. Пятый байт обычно имеет очень низкие значения: чаще всего встречаются 02 и 03, а максимальным значением кажется является 05. Шестой байт файла очень часто равен нулю — но подчас он содержит гораздо большие значения, например 32 или 2C. В этой паре наше предположение о распределённых в интервале значениях не особо подтверждается.
Внимательнее изучаем исходные значения
Мы можем проверить свою догадку, использовав
od для генерации шестнадцатеричного дампа. Утилита od похожа xxd, но обеспечивает гораздо больший выбор форматов вывода. Мы можем использовать её, чтобы сдампить вывод в виде 16-битных десятеричных целых чисел:
Опция -t утилиты od указывает формат вывода. В данном случае u обозначает беззнаковые десятеричные числа, а 2 обозначает два байта на запись. (Также этот формат можно задать с помощью опции -d.)
$ for f in levels/* ; do od -tu2 $f | sed -n 1p ; done | less 0000000 35 476 3 1024 257 778 2819 8995 0000000 45 447 3 5376 257 802 10499 8738 0000000 43 417 259 1281 0 262 1794 1285 0000000 29 211 2 768 257 516 1282 513 0000000 45 378 3 1536 5140 263 2305 771 0000000 49 520 2 768 257 517 1538 4883 0000000 26 183 2 768 1 517 1538 257 0000000 26 262 3 1280 256 262 1793 771 0000000 32 378 2 768 514 260 1281 10240 0000000 58 164 2 768 10280 10244 1282 771 0000000 38 218 3 1024 1797 265 2561 771 0000000 36 240 3 1024 771 1029 1796 257 0000000 42 495 3 1280 257 5126 1792 771 0000000 44 396 3 1024 771 5 1793 257 0000000 42 256 3 1024 771 261 1793 1028 0000000 27 365 2 768 257 517 1538 768 0000000 30 279 2 768 514 260 1281 4864 0000000 50 494 15 5376 257 3879 10511 5140 0000000 42 347 3 1280 771 262 1793 5140 0000000 44 394 2 768 514 260 1281 771 0000000 29 156 5634 1046 0 5637 1793 1282 0000000 32 225 2 768 257 516 1282 771 0000000 32 294 3 1024 771 517 1794 257 0000000 31 246 12801 772 0 12805 1586 1028 lines 1-24/148 (more)
Эти выходные данные показывают, что наши догадки о первых нескольких байтах были верными. Мы видим, что первое 16-битное значение находится в десятеричном интервале 20–70, а второе 16-битное значение — в десятеричном интервале 100–600. Однако последующие значения ведут себя не так хорошо. В них проявляются определённые паттерны (например, в четвёртой позиции на удивление часто встречается 1024), но они не обладают повторяемостью, свойственной первым значениям файла.
Поэтому давайте предварительно допустим, что первые четыре байта файла особые и состоят из двух 16-битных значений. Так как они находятся в самом начале файла, то скорее всего являются метаданными и помогают определить, как считывать остальную часть файла.
На самом деле, второй интервал значений (100–600) довольно близок к замеченному нами ранее интервалу размеров файлов (208–680). Возможно, это не совпадение? Давайте выдвинем гипотезу: хранящееся в третьем и четвёртом байтах файла 16-битное значение коррелирует с общим размером файла. Теперь, когда у нас есть гипотеза, мы можем её проверить. Посмотрим, действительно ли у больших файлов в этом месте постоянно большие значения, а у маленьких — маленькие.
Для отображения размера файла в байтах без всякой другой информации можно использовать wc с опцией -c. Аналогично, можно добавить к od опции, позволяющие выводить только интересующие нас значения. Затем мы можем использовать подстановку команд для записи этих значений в переменные оболочки и отобразить их вместе:
Опция -An утилиты od отключает самую левый столбец, в котором отображается смещение в файле, а -N4 приказывает od остановиться после первых 4 байтов файла.
$ for f in levels/* ; do size=$(wc -c <$f) ; data=$(od -tuS -An -N4 $f) ; echo "$size: $data" ; done | less 585: 35 476 586: 45 447 550: 43 417 302: 29 211 517: 45 378 671: 49 520 265: 26 183 344: 26 262 478: 32 378 342: 58 164 336: 38 218 352: 36 240 625: 42 495 532: 44 396 386: 42 256 450: 27 365 373: 30 279 648: 50 494 477: 42 347 530: 44 394 247: 29 156 325: 32 225 394: 32 294 343: 31 246
Посмотрев на эти выходные данные, можно увидеть, что значения приблизительно коррелируют. Меньшие файлы обычно имеют во второй позиции меньшие значения, а большие файлы — большие значения. Однако корреляция не точная, и стоит заметить, что размер файла всегда значительно больше, чем хранящееся в нём значение.
Кроме того, первое 16-битное значение тоже обычно бывает больше при больших размерах файлов, но совпадение тоже не совсем полное, и можно легко найти примеры файлов среднего размера с относительно большими значениями в первой позиции. Но возможно если мы сложим эти два значения, их сумма будет лучше коррелировать с размером файла?
Мы можем использовать read для извлечения двух чисел из выходных данных od в отдельные переменные, а затем использовать арифметику командной оболочки для нахождения их суммы:
Команда оболочки read не может использоваться с правой части вертикальной черты, потому что переданные в конвейер команды выполняются в дочернем командном процессоре (subshell), который при выходе берёт с собой свои переменные окружения в битоприёмник. Поэтому вместо этого нам необходимо воспользоваться функцией подстановки процессов bash и направить вывод od во временный файл, который затем можно перенаправить в команду read.
$ for f in levels/* ; do size=$(wc -c <$f) ; read v1 v2 < <(od -tuS -An -N4 $f) ; sum=$(($v1 + $v2)) ;
echo "$size: $v1 + $v2 = $sum" ; done | less
585: 35 + 476 = 511
586: 45 + 447 = 492
550: 43 + 417 = 460
302: 29 + 211 = 240
517: 45 + 378 = 423
671: 49 + 520 = 569
265: 26 + 183 = 209
344: 26 + 262 = 288
478: 32 + 378 = 410
342: 58 + 164 = 222
336: 38 + 218 = 256
352: 36 + 240 = 276
625: 42 + 495 = 537
532: 44 + 396 = 440
386: 42 + 256 = 298
450: 27 + 365 = 392
373: 30 + 279 = 309
648: 50 + 494 = 544
477: 42 + 347 = 389
530: 44 + 394 = 438
247: 29 + 156 = 185
325: 32 + 225 = 257
394: 32 + 294 = 326
343: 31 + 246 = 277
lines 1-24/148 (more)
Сумма двух числе тоже приблизительно коррелирует с размером файла, но они всё равно не совсем совпадают. Насколько же они отличаются? Давайте продемонстрируем их разность:
$ for f in levels/* ; do size=$(wc -c <$f) ; read v1 v2 < <(od -tuS -An -N4 $f) ; diff=$(($size - $v1 - $v2)) ;
echo "$size = $v1 + $v2 + $diff" ; done | less
585 = 35 + 476 + 74
586 = 45 + 447 + 94
550 = 43 + 417 + 90
302 = 29 + 211 + 62
517 = 45 + 378 + 94
671 = 49 + 520 + 102
265 = 26 + 183 + 56
344 = 26 + 262 + 56
478 = 32 + 378 + 68
342 = 58 + 164 + 120
336 = 38 + 218 + 80
352 = 36 + 240 + 76
625 = 42 + 495 + 88
532 = 44 + 396 + 92
386 = 42 + 256 + 88
450 = 27 + 365 + 58
373 = 30 + 279 + 64
648 = 50 + 494 + 104
477 = 42 + 347 + 88
530 = 44 + 394 + 92
247 = 29 + 156 + 62
325 = 32 + 225 + 68
394 = 32 + 294 + 68
343 = 31 + 246 + 66
lines 1-24/148 (more)
Разность, или значение «остатка», отображается в самой правой части вывода. Это значение не совсем попадает в постоянный паттерн, но, похоже, остаётся примерно в ограниченном интервале 40–120. И снова, чем больше файлы, тем обычно больше их значения остатков. Но иногда у мелких файлов тоже бывают большие значения остатков, так что это не так постоянно, как бы нам хотелось.
Тем не менее, стоит заметить, что значения остатков никогда не бывают отрицательными. Поэтому мысль о том, что эти два значения метаданных указывают на подразделы файла, сохраняет свою привлекательность.
(Если вы достаточно внимательны, то уже увидели нечто, дающее подсказку о пока незамеченной связи. Если не увидели, то продолжайте читать; тайна вскоре будет раскрыта.)
Более масштабные перекрёстные сравнения файлов
На этом этапе было бы неплохо иметь возможность перекрёстно сравнивать больше, чем 16 байт за раз. Для этого нам потребуется другой тип визуализации. Один из хороших подходов — создать изображение, в котором каждый пиксель обозначает отдельный байт одного из файлов, а цвет обозначает значение этого байта. Изображение может показать срез всех 148 файлов за раз, если каждый файл данных будет обозначаться одной строкой пикселей изображения. Так как все файлы имеют разный размер, мы возьмём по 200 первых байт каждого, чтобы построить прямоугольное изображение.
Проще всего будет построить изображение в градациях серого, в котором значение каждого байта соответствует разным уровням серого. Можно очень просто создать файл PGM с нашими данными, потому что заголовок PGM состоит только из ASCII-текста:
$ echo P5 200 148 255 >hdr.pgm
Что такое файл PGM? PGM, что расшифровывается как «portable graymap» («платформонезависимая карта оттенков серого») — это один из трёх форматов графических файлов, которые созданы ради чрезвычайной простоты считывания и записи: после заголовка в ASCII, каждый байт описывает цвет одного пикселя в градациях серого. Два остальных формата файлов из этого семейства — это PBM («portable bitmap», «платформонезависимая битовая карта»), описывающий монохромные изображения как 8 пикселей на байт, и PPM («portable pixmap», «платформонезависимая пиксельная карта»), которая описывает изображения как 3 байта на пиксель.
P5 — это начальная сигнатура, обозначающая формат файлов PGM. Следующие два числа, 200 и 148, задают ширину и высоту изображения, а последнее, 255, указывает максимальное значение на пиксель. Заголовок PGM завершается переходом на новую строку, после которого идут пиксельные данные. (Стоит заметить, что заголовок PGM чаще всего разбит на три отдельных строки текста, но стандарт PGM требует только, чтобы элементы были разделены каким-нибудь пробельным символом (whitespace).)
Мы можем использовать утилиту head, чтобы извлечь из каждого файла первые 200 байт:
$ for f in levels/* ; do head -c200 $f ; done >out.pgm
Затем мы можем конкатенировать их с заголовком и создать отображаемое изображение:
xview — это старая программа X для отображения изображений в окне. Можете заменить её своим любимой программой просмотра изображений, например, утилитой display из ImageMagick, но учтите, что есть на удивление много утилит просмотра изображений, которые не принимают файл изображения, перенаправленный на стандартный вход.
$ cat hdr.pgm out.pgm | xview /dev/stdin
Если вам сложно рассмотреть детали на тёмном изображении, то можете выбрать другую цветовую схему. Используйте утилиту
pgmtoppm из ImageMagick, чтобы преобразовать пиксели в другой диапазон цветов. Эта версия создаст «негативное» изображение:
$ cat hdr.pgm out.pgm | pgmtoppm white-black | xview /dev/stdin
А эта версия делает низкие значения жёлтыми, а высокие — синими:
$ cat hdr.pgm out.pgm | pgmtoppm yellow-blue | xview /dev/stdin
Видимость цветов — очень субъективный вопрос, поэтому можете поэкспериментировать, и выбрать, что лучше для вас. Как бы то ни было, изображение 200 × 148 довольно мало, так что лучше всего повысить видимость, увеличив его размер:
$ cat hdr.pgm out.pgm | xview -zoom 300 /dev/stdin

Изображение тёмное, и это означает, что большинство байтов содержит маленькие значения. Контрастирует с ним заметная полоса в основном ярких пикселей ближе к левому краю. Эта полоса расположена в третьем байте файла, который, как мы говорили выше, варьируется в полном интервале значений.
И хотя за пределами третьего байта есть не так много высоких значений, когда они появляются, то часто состоят из серий, создавая на изображении короткие яркие полоски. Некоторые из этих серий периодически прерываются, создавая эффект пунктирной линии. (Возможно, при правильном подборе цвета можно будет заметить такие последовательности и в более тёмных цветах.)
При внимательном изучении изображения можно понять, что в основном в левой части доминируют небольшие вертикальные полосы. Эти полосы говорят нам о некой повторяемости в большинстве файлов. Но не во всех файлах — время от времени появляются строки пикселей, где полосы прерываются — но этого более чем достаточно, чтобы определить наличие реального паттерна. Этот паттерн пропадает в правой части изображения, тёмный фон из полос уступает место чему-то более шумному и неопределённому. (Похоже, что полосы также отсутствуют в самой левой части изображения, но, повторюсь, возможно, что при использовании другой цветовой схемы можно увидеть, что они начинаются ближе к левому краю, чем это кажется здесь.)
Полосы состоят из тонких линий из немного более ярких пикселей на фоне из немного более тёмных пикселей. Следовательно, этот графический паттерн должен коррелировать с паттерном файлов данных, в которых немного бОльшие значения одинаково рассеяны среди немного меньших значений байтов. Похоже, что полосы истощаются примерно посередине изображения. Так как на нём показаны первые 200 байт файлов, следует ожидать, что байтовый паттерн заканчивается примерно после 100 байт.
Тот факт, что эти паттерны изменяются в разных файлах данных, должен привести нас к вопросу: как будут выглядеть файлы после первых 200 байт. Ну, мы можем легко заменить утилиту head утилитой tail и посмотреть, как выглядят последние 200 байт:
$ for f in levels/* ; do tail -c200 $f ; done >out.pgm ; cat hdr.pgm out.pgm | xview -zoom 300 /dev/stdin

Мы сразу же видим, что эта область файлов данных сильно отличается. Здесь намного чаще встречаются большие значения байтов, особенно ближе к концу файла. (Однако как и раньше, они предпочитают группироваться вместе, покрывая изображение яркими горизонтальными полосками.) Похоже, что частота высоких значений байтов увеличивается почти до самого конца, где резко обрывается и примерно в последних десяти-двенадцати байтах сменяется низкими значениями. И паттерн здесь тоже не универсален, но он слишком стандартный, чтобы оказаться совпадением.
Возможно, в середине файлов могут быть и другие области, которые мы пока не рассматривали. Следующее, что мы хотим сделать — исследовать таким образом файлы целиком. Но так как все файлы имеют разные размеры, их нельзя расположить в красивом прямоугольном массиве пикселей. Мы можем заполнить конец каждой строки чёрными пикселями, но будет лучше, если мы изменим их размер так, чтобы все строки были одинаковой ширины и пропорциональные области разных файлов более-менее совпадали.
И мы на самом деле можем это сделать, приложив чуть больше усилий. Можно воспользоваться Python и его библиотекой для работы с изображениями PIL («Pillow»):
Файл showbytes.py:
import sys
from PIL import Image
# Retrieve the full list of data files.
filenames = sys.argv[1:]
# Create a grayscale image, its height equal to the number of data files.
width = 750
height = len(filenames)
image = Image.new('L', (width, height))
# Fill in the image, one row at a time.
for y in range(height):
# Retrieve the contents of one data file.
data = open(filenames[y]).read()
linewidth = len(data)
# Turn the data into a pixel-high image, each byte becoming one pixel.
line = Image.new(image.mode, (linewidth, 1))
linepixels = line.load()
for x in range(linewidth):
linepixels[x,0] = ord(data[x])
# Stretch the line out to fit the final image, and paste it into place.
line = line.resize((width, 1))
image.paste(line, (0, y))
# Magnify the final image and display it.
image = image.resize((width, 3 * height))
image.show()
Когда мы вызовем этот скрипт, использовав качестве аргументов полный список файлов данных, он создаст полное изображение и отобразит его в отдельном окне:
$ python showbytes.py levels/*
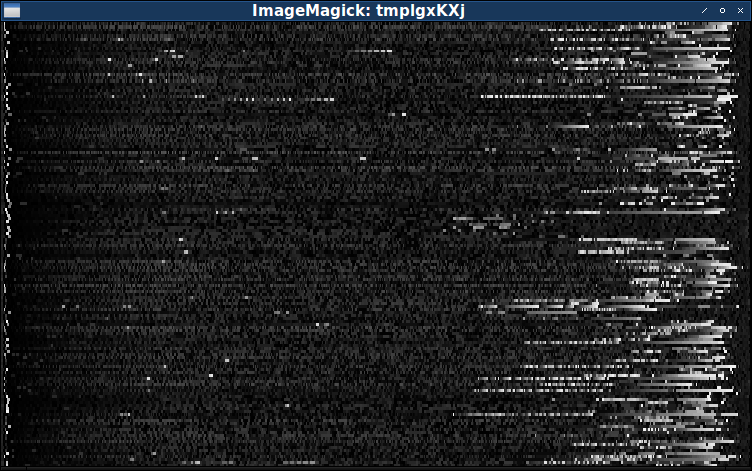
К сожалению, хоть это изображение и является полным, оно не показывает нам ничего нового. (А на самом деле показывает даже меньше, потому что изменение размера уничтожило паттерн из полос.) Наверно, для изучения всего множества данных нам потребуется процесс визуализации получше.
Характеризуем данные
Учтя это, давайте ненадолго остановимся и выполним полную перепись данных. Нам нужно знать, не отдают ли файлы данных предпочтение определённым значениям байтов. Например, если каждое значение обычно бывает одинаково повторяющимся, то это будет сильным доказательством того, что файлы на самом деле сжаты.
Для полной переписи значений достаточно всего нескольких строк на Python:
Файл census.py:
import sys
data = sys.stdin.read()
for c in range(256):
print c, data.count(chr(c))
Засунув все данные в одну переменную, мы можем выполнить подсчёт частоты появления каждого байтового значения.
$ cat levels/* | python ./census.py | less 0 2458 1 2525 2 1626 3 1768 4 1042 5 1491 6 1081 7 1445 8 958 9 1541 10 1279 11 1224 12 845 13 908 14 859 15 1022 16 679 17 1087 18 881 19 1116 20 1007 21 1189 22 1029 23 733 lines 1-24/256 (more)
Мы видим, что чаще всего встречаются байтовые значения 0 и 1, следующими по частоте идут 2 и 3, после чего количество продолжает уменьшаться (хотя и с меньшим постоянством). Чтобы лучше визуализировать эти данные, мы можем передать вывод в
gnuplot и превратить эту перепись в гистограмму:
Опция -p утилиты gnuplot приказывает не закрывать окно с графиком после завершения работы gnuplot.
$ cat levels/* | python ./census.py | gnuplot -p -e 'plot "-" with boxes'
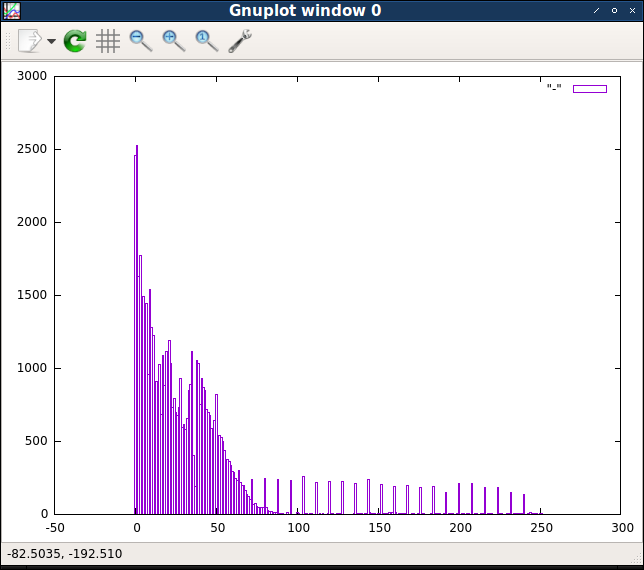
Очень заметно, что первые несколько байтовых значений встречаются гораздо чаще, чем все остальные. Несколько следующих значений тоже достаточно распространены, а затем частоты значений примерно от 50 начинают снижаться по плавной кривой вероятностей. Однако есть подмножество высоких значений, равномерно отделённых друг от друга, частота которых кажется довольно стабильной. Посмотрев на исходные выходные данные, мы можем убедиться, что это подмножество состоит из значений, без остатка делящихся на восемь.
Эти различия в количестве значений намекают, что существует несколько разных «классов» байтовых значений, поэтому будет логично посмотреть, как распределены эти классы. Первой группой байтовых значений будут самые низкие значения: 0, 1, 2 и 3. Тогда второй группой могут быть значения от 4 до 64. А третьей группой будут значения выше 64, которые без остатка делятся на 8. Всё остальное, в том числе и не делящиеся на 8 значения больше 64, будут составлять четвёртую и последнюю группу.
С учётом всего этого мы можем изменить последний написанный скрипт генерации изображений. Вместо того, чтобы отображать отдельным цветом настоящие значения каждого байта, давайте просто покажем, к какой группе относится каждый байт. Можно назначить каждой из четырёх групп уникальный цвет, и это поможет нам увидеть, действительно ли определённые значения обычно появляются в определённых местах.
Файл showbytes2.py:
import sys
from PIL import Image
# Retrieve the full list of data files.
filenames = sys.argv[1:]
# Create a color image, its height equal to the number of data files.
width = 750
height = len(filenames)
image = Image.new('RGB', (width, height))
# Fill in the image, one row at a time.
for y in range(height):
# Retrieve the contents of one data file.
data = open(filenames[y]).read()
linewidth = len(data)
# Turn the data into a pixel-high image, each byte becoming one pixel.
line = Image.new(image.mode, (linewidth, 1))
linepixels = line.load()
# Determine which group each byte belongs to and assign it a color.
for x in range(linewidth):
byte = ord(data[x])
if byte < 0x04: linepixels[x,0] = (255, 0, 0)
elif byte < 0x40: linepixels[x,0] = (0, 255, 0)
elif byte % 8 == 0: linepixels[x,0] = (0, 0, 255)
else: linepixels[x,0] = (255, 255, 255)
# Paste the line of pixels into the final image, stretching to fit.
line = line.resize((width, 1))
image.paste(line, (0, y))
# Magnify the final image and display it.
image = image.resize((width, 3 * height))
image.show()
Мы назначили четырём группам красный, зелёный, синий и белый цвета. (Вы опять же можете попробовать выбрать другие цвета, соответствующие вашим предпочтениям.)
$ python showbytes2.py levels/*

Благодаря этому изображению мы можем предварительно подтвердить правильность разделения файлов данных на пять частей:
- Четырёхбайтный заголовок, который мы уже нашли ранее.
- Область полос, которую мы не видим непосредственно, но она содержит множество красных пикселей (т.е. низких байтовых значений).
- Основная часть, в которой у большинства файлов в основном находятся зелёные пиксели (т.е значения ниже 64).
- Часть ближе к концу, где внезапно начинают доминировать синие пиксели.
- Короткая последняя часть, которая внезапно возвращается к зелёным значениям.
Благодаря этим цветам понятно, что в четвёртой части, где преобладают высокие байтовые значения, как это видно на изображении в градациях серого, особенно преобладают высокие байтовые значения, делящиеся на 8.
Из предыдущего изображения мы знаем, что вторая часть, то есть часть с полосами, растягивается за почти полностью красную область. На самом деле, на одном из первых изображений мы видели, что часть с полосами, идя слева направо, в среднем медленно светлеет.
Мы снова видим, что незелёные пиксели с основной третьей части время от времени образуют пунктирные паттерны из перемежающихся зелёных и красных пикселей (или синих, или белых). Однако этот паттерн не особо регулярен, и может быть мнимым.
Разумеется, это деление файла на пять частей очень условно. Четвёртая часть с высокими байтовыми значениями, делящимися на восемь, может оказаться всего лишь концом третьей части. Или может оказаться, что лучше всего разделить крупную третью часть на несколько частей, которые мы ещё не определили. На этом этапе обнаружение частей больше помогает нам находить места для дальнейшего исследования. Нам пока достаточно знать, что существуют части, в которых меняется общий состав байтовых значений, а приблизительное представление об их размере поможет нам продолжать исследования.
Поиск структуры
Что нам искать дальше? Ну, как и раньше, проще всего начать с верха файла. Или, скорее, рядом с верхом. Так как мы уже довольно уверенно определили первую часть как четырёхбайтный заголовок, давайте внимательнее рассмотрим то, что идёт дальше — область, которую мы называем второй частью, или частью полос. Эти полосы — самый сильный намёк на существование структуры, поэтому искать новые свидетельства наличия паттерна лучше искать здесь.
(На время мы предположим, что паттерн из полос начинается сразу же после первых четырёх байтов. Визуально это неочевидно, но кажется вероятным, и исследование байтовых значений быстро должно показать нам правду.)
Давайте вернёмся к hex dump, на этот раз сосредоточившись на второй части. Помните, что мы ожидаем найти повторяющийся паттерн немного более высоких значений, равномерно распределённых среди немного более низких значений.
Опция -s4 приказывает xxd пропустить первые 4 байта файла.
$ for f in levels/* ; do xxd -s4 $f | sed -n 1p ; done | less 00000004: 0200 0003 0202 0401 0105 0303 0700 0108 ................ 00000004: 0201 0104 0000 0504 0407 0202 0902 010a ................ 00000004: 0300 0004 0303 0504 0407 0505 0801 0109 ................ 00000004: 0300 0009 0202 1203 0313 0909 1401 0115 ................ 00000004: 0203 0305 0000 0602 0207 0505 0901 010a ................ 00000004: 0203 0304 0000 0502 0206 0404 0901 010a ................ 00000004: 0300 0005 022a 0602 2907 0303 0902 000a .....*..)....... 00000004: 0203 0305 0000 0605 0507 0101 0802 0209 ................ 00000004: 0300 0007 0303 0901 010a 0707 0b09 090c ................ 00000004: 0300 0004 0101 0903 030e 0404 1609 0920 ............... 00000004: 0200 0003 1313 0402 0205 0013 0701 0109 ................ 00000004: 0500 0006 0505 0701 0109 0606 0e07 070f ................ 00000004: 0100 0003 0101 0a03 030b 0a0a 0e32 3216 .............22. 00000004: 0300 0004 0705 0903 030a 0606 0b08 080c ................ 00000004: 0200 0003 0701 0402 0209 0501 0a08 080b ................ 00000004: 0200 0003 0202 0901 010a 0303 0b05 010d ................ 00000004: 0200 0003 0202 0403 0305 0101 0904 040a ................ 00000004: 0300 0007 0303 0f01 0115 0707 2114 1422 ............!.." 00000004: 0200 0003 0202 0403 0309 0101 0a04 040b ................ 00000004: 0231 3103 0202 0500 0006 0303 0701 0109 .11............. 00000004: 0200 0003 0202 0b32 320c 0303 0e08 0811 .......22....... 00000004: 0201 0103 0000 0902 020a 0303 0b09 090c ................ 00000004: 0200 0003 0202 0a01 010b 0303 0d0b 0b0f ................ 00000004: 0300 0005 0303 0701 0109 0001 0b05 051b ................ lines 27-50/148 (more)
Внимательно посмотрев на последовательность байтов в строке, мы можем увидеть паттерн, по которому первый, четвёртый, седьмой и десятый байт больше, чем его ближайшие соседи. Этот паттерн неидеален, в нём есть исключения, но он определённо достаточно устойчив, чтобы создавать визуальную повторяемость полос, замеченную на всех изображениях. (И его достаточно для подтверждения нашего предположения о том, что паттерн из полос начинается сразу после четырёхбайтного заголовка.)
Постоянство этого паттерна явно предполагает, что эта часть файла является массивом или таблицей, и каждая запись в массиве имеет длину три байта.
Можно настроить формат шестнадцатеричного дампа, чтобы проще увидеть вывод как серию триплетов:
Опция -g3 задаёт группирование по трём байтам вместо двух. Опция -c18 задаёт 18 байтов (число, кратное 3) в строке вместо 16.
$ for f in levels/* ; do xxd -s4 -g3 -c18 $f | sed -n 1p ; done | less 00000004: 050000 060505 070101 090606 0e0707 0f0001 .................. 00000004: 010000 030101 0a0303 0b0a0a 0e3232 161414 .............22... 00000004: 030000 040705 090303 0a0606 0b0808 0c0101 .................. 00000004: 020000 030701 040202 090501 0a0808 0b0101 .................. 00000004: 020000 030202 090101 0a0303 0b0501 0d0302 .................. 00000004: 020000 030202 040303 050101 090404 0a0302 .................. 00000004: 030000 070303 0f0101 150707 211414 221313 ............!..".. 00000004: 020000 030202 040303 090101 0a0404 0b0001 .................. 00000004: 023131 030202 050000 060303 070101 090505 .11............... 00000004: 020000 030202 0b3232 0c0303 0e0808 110b0b .......22......... 00000004: 020101 030000 090202 0a0303 0b0909 0c0a0a .................. 00000004: 020000 030202 0a0101 0b0303 0d0b0b 0f2323 ................## 00000004: 030000 050303 070101 090001 0b0505 1b0707 .................. 00000004: 022323 030000 040202 050303 030101 070505 .##............... 00000004: 031414 050000 060303 070505 080101 090707 .................. 00000004: 030000 050202 060303 070505 080101 090606 .................. 00000004: 030202 040000 050303 070404 080005 090101 .................. 00000004: 030202 040000 050303 090404 1d0101 1f0909 .................. 00000004: 020000 050303 060101 070202 0f0300 110505 .................. 00000004: 050000 070101 0c0505 0d0007 110c0c 120707 .................. 00000004: 030202 050000 060303 070505 080101 090606 .................. 00000004: 020000 030101 050202 060505 070100 080303 .................. 00000004: 020000 030202 050303 090101 0a0505 0b0302 .................. 00000004: 022c2c 030000 040202 020303 050101 060202 .,,............... lines 38-61/148 (more)
В отформатированном таким образом дампе начинают проявляться некоторые другие особенности этого паттерна. Как и раньше, первый байт каждого триплета обычно больше окружающих его байтов. Также можно заметить, что второй и третий байты каждого триплета часто дублируются. Пройдя вниз по первому столбцу, мы увидим, что большинство значений вторых и третьих байтов равны
0000. Но ненулевые значения тоже часто встречаются попарно, например 0101 или 2323. Этот паттерн тоже неидеален, но в нём слишком много общего, чтобы это было совпадением. А взглянув на столбец ASCII справа, мы убедимся, что когда у нас бывают байтовые значения, соответствующие печатаемому символу ASCII, то они часто встречаются парами.
Ещё один стоящий упоминания паттерн, который заметен не сразу: первый байт каждого триплета при движении слева направо увеличивается. Хотя этот паттерн менее заметен, устойчивость его высока; нужно просмотреть много строк, прежде чем мы найдём первое несоответствие. А байты обычно увеличиваются на небольшие значения, однако не представляющие никакого регулярного паттерна.
При изучении исходного изображения мы заметили, что часть с полосами кончается в каждом файле не в одном и том же месте. Существует переход от создающего полосы паттерна слева к выглядящему случайно шуму справа, но этот переход происходит для каждой строки пикселей в разных точках. Это подразумевает, что должен существовать некий маркер, чтобы считывающая файл данных программа могла понять, где заканчивается массив и начинается другое множество данных.
Давайте вернёмся к дампу только первого уровня, чтобы изучить файл целиком:
$ xxd -s4 -g3 -c18 levels/lesson_1.pak 00000004: 020000 040202 050404 070505 080707 090001 .................. 00000016: 0a0101 0b0808 0d0a0a 110023 150907 180200 ...........#...... 00000028: 22090d 260911 270b0b 280705 291e01 272705 "..&..'..(..)..''. 0000003a: 020d01 220704 090209 0a0215 042609 250111 ...".........&.%.. 0000004c: 150222 1d0124 011d0d 010709 002000 1b0400 .."..$....... .... 0000005e: 1a0020 152609 1f0033 002911 152223 02110d .. .&...3.).."#... 00000070: 010726 091f18 291115 09181a 022302 1b0215 ..&...)......#.... 00000082: 22011c 011c0d 0a0704 090201 020128 260123 ".............(&.# 00000094: 150509 020121 150522 0a2727 0b0504 00060b .....!..".''...... 000000a6: 082804 18780b 082804 18700b 082804 186400 .(..x..(..p..(..d. 000000b8: 17101e 1e1a19 010300 0e1a17 17100e 1f010e .................. 000000ca: 13141b 291f1a 001210 1f011b 0c1e1f 011f13 ...).............. 000000dc: 10010e 13141b 001e1a 0e1610 1f2d00 201e10 .............-. .. 000000ee: 011610 24291f 1a011a 1b1019 000f1a 1a1d1e ...$)............. 00000100: 2d02
Изучая последовательности триплетов, мы можем предварительно предположить, что часть с полосами в этих данных заканчивается после 17 триплетов, по смещению
00000036. Это не точно, но первый байт каждого триплета постоянно увеличивает своё значение, а затем уменьшается на восемнадцатом триплете. Ещё одно доказательство: в восемнадцатом триплете второй байт имеет то же значение, что и первый. Этого мы ещё не замечали, но если вернёмся назад и посмотрим, то увидим, что первый байт никогда не равен второму или третьему байту.
Если наша теория о маркерах верна, то есть две возможности. Во-первых, возможно, после части с полосами существует некое специальное байтовое значение (сразу после семнадцатого триплета). Во-вторых, вероятно, существует хранимое где-то значение, равное размеру части с полосами. Этот размер может равен числу 17 (то есть обозначает количество триплетов), или 51 (обозначает общее количество байтов в части), или 55 (51 плюс 4, то есть смещение файла, в котором заканчивается эта часть).
Для первого варианта двойное байтовое значение может быть маркером конца части (учитывая то, что такая последовательность никогда не встречается во второй части). Однако внимательное изучение нескольких других файлов данных противоречит этой идее, потому что такой паттерн нигде больше не появляется.
Для второго варианта очевидно будет поискать индикатор размера в первой части. Узрите — первое 16-битное значение в четырёхбайтном заголовке файла равно 17:
$ od -An -tuS -N4 levels/lesson_1.pak
17 203
Если наша теория верна, тогда это значение определяет не сам размер части с полосами, а количество трёхбайтных записей. Чтобы проверить эту идею, давайте вернёмся к вычислениям, где мы сравнивали сумму двух 16-битных целочисленных значений с размером файла. На этот раз мы умножим первое число на три, чтобы получить настоящий размер в байтах:
$ for f in levels/* ; do size=$(wc -c <$f) ; read v1 v2 < <(od -tuS -An -N4 $f) ; diff=$(($size - 3 * $v1 - $v2)) ;
echo "$size = 3 * $v1 + $v2 + $diff" ; done | less
585 = 3 * 35 + 476 + 4
586 = 3 * 45 + 447 + 4
550 = 3 * 43 + 417 + 4
302 = 3 * 29 + 211 + 4
517 = 3 * 45 + 378 + 4
671 = 3 * 49 + 520 + 4
265 = 3 * 26 + 183 + 4
344 = 3 * 26 + 262 + 4
478 = 3 * 32 + 378 + 4
342 = 3 * 58 + 164 + 4
336 = 3 * 38 + 218 + 4
352 = 3 * 36 + 240 + 4
625 = 3 * 42 + 495 + 4
532 = 3 * 44 + 396 + 4
386 = 3 * 42 + 256 + 4
450 = 3 * 27 + 365 + 4
373 = 3 * 30 + 279 + 4
648 = 3 * 50 + 494 + 4
477 = 3 * 42 + 347 + 4
530 = 3 * 44 + 394 + 4
247 = 3 * 29 + 156 + 4
325 = 3 * 32 + 225 + 4
394 = 3 * 32 + 294 + 4
343 = 3 * 31 + 246 + 4
lines 1-24/148 (more)
Ага! После этого изменения общая сумма из заголовка всегда точно на четыре меньше размера всего файла данных. А поскольку четыре — это ещё и количество байтов в заголовке, очевидно, что это не совпадение. Первое число даёт нам количество трёхбайтных записей в таблице, а второе число — количество байтов, составлящих оставшуюся часть файла данных.
Мы обнаружили постоянную формулу, а значит, полностью теперь понимаем, что означают числа в первой части.
(Кстати, здесь есть тот самый тайный паттерн, который могли заметить внимательные читатели. При внимательном изучении уравнений становится понятно, что когда файлы имеют одинаковое первое число, у них получается одинаковая разность остатка. Так получается, потому что разность всегда в два раза больше значения первого числа. Это неочевидный паттерн, но кропотливый или удачливый наблюдатель мог бы его заметить.)
Итак, мы можем сказать, что файл имеет три основные части:
- четырёхбайтный заголовок;
- таблица трёхбайтных записей; и
- оставшаяся часть файла, в которой, предположительно, находится бОльшая часть данных.
(Следовательно, другие части, которые мы приблизительно определили ранее, должны быть подразделами третьей части.)
Интерпретируем метаданные
С учётом этой схемы, было бы логично предположить, что записи в таблице второй части являются некими метаданными, которые необходимы для интерпретирования данных третьей части.
Но какие же метаданные содержит эта таблица?
Выше мы заметили, что есть пара признаков того, что файл данных может быть сжат. (Теперь это кажется ещё правдоподобнее, ведь мы знаем, что третья часть каждого файла, предположительно содержащая данные каждого уровня, имеет размер всего 100–600 байт.) Если это так, то вполне возможно, что таблица, предваряющая основные данные, содержит метаданные сжатия — некий словарь, применяемый во время распаковки. Например, перед данными, закодированными алгоритмом Хаффмана, обычно есть словарь, сопоставляющий исходные байтовые значения с битовыми последовательностями. Хоть мы и не ожидаем, что эти файлы закодированы алгоритмом Хаффмана (так как данные демонстрируют чёткие паттерны на уровне байтов, то есть вряд ли являются битовым потоком), было бы вполне разумно попробовать интерпретировать эту таблицу как словарь распаковки.
(Разумеется, не в каждом типе сжатия используется хранимый словарь. Например, алгоритм deflate, применяемый в gzip и zlib, позволяет воссоздавать словарь непосредственно из потока данных. Но такие случаи скорее являются исключением, чем правилом.)
Обычно запись словаря состоит из двух частей: ключа и значения. Разумеется, иногда ключ является подразумеваемым, например, когда он упорядочен не в таблицу поиска, а в массив. Однако мы уже заметили, что трёхбайтные записи как будто бы состоят из двух частей — в частности, первый байт каждой записи следует паттерну, чётко отличающемуся от паттерна второго и третьего байтов. С учётом этого, разумной первой гипотезой будет считать первый байт ключом, а оставшиеся два байта — значением.
Если это так, то один из простейших способов интерпретации части с полосами состоит в том, что первый байт — это байтовое значение, которое нужно заменять в сжатых данных, а второй и третий байты — значение, которыми его нужно заменять. Результат, создаваемый этой схемой, определённо будет больше, хоть и непонятно, насколько. Как бы то ни было, это вполне логичная гипотеза, и её достаточно легко проверить. Мы можем написать на Python короткую программу, реализующую эту схему распаковки:
Файл decompress.py:
import struct
import sys
# Read the compressed data file.
data = sys.stdin.read()
# Extract the two integers of the four-byte header.
tablesize, datasize = struct.unpack('HH', data[0:4])
data = data[4:]
# Separate the dictionary table and the compressed data.
tablesize *= 3
table = data[0:tablesize]
data = data[tablesize:datasize]
# Apply the dictionary entries to the data section.
for n in range(0, len(table), 3):
key = table[n]
val = table[n+1:n+3]
data = data.replace(key, val)
# Output the expanded result.
sys.stdout.write(data)
Теперь мы можем проверить этот скрипт на примере файла данных:
$ python ./decompress.py <levels/lesson_1.pak | xxd
00000000: 0b0b 0b0b 0404 0000 0a0a 0109 0d05 0502 ................
00000010: 0200 0100 0000 0101 0100 0009 0702 0209 ................
00000020: 1100 0125 0100 2309 0700 0009 0d1d 0124 ...%..#........$
00000030: 011d 0a0a 0105 0500 0100 2000 1b02 0200 .......... .....
00000040: 1a00 2009 0709 1100 011f 0033 001e 0100 .. ........3....
00000050: 2309 0709 0d23 0000 0023 0a0a 0105 0509 #....#...#......
00000060: 1100 011f 0200 1e01 0023 0907 0001 0200 .........#......
00000070: 1a00 0023 0000 1b00 0009 0709 0d01 1c01 ...#............
00000080: 1c0a 0a01 0105 0502 0200 0100 0001 0000 ................
00000090: 0107 0509 1101 2309 0704 0400 0100 0001 ......#.........
000000a0: 2109 0704 0409 0d01 010b 0b0b 0b08 0804 !...............
000000b0: 0402 0200 0608 0807 0707 0502 0202 0078 ...............x
000000c0: 0808 0707 0705 0202 0200 7008 0807 0707 ..........p.....
000000d0: 0502 0202 0064 0017 101e 1e1a 1901 0300 .....d..........
000000e0: 0e1a 1717 100e 1f01 0e13 141b 1e01 1f1a ................
000000f0: 0012 101f 011b 0c1e 1f01 1f13 1001 0e13 ................
00000100: 141b 001e 1a0e 1610 1f2d 0020 1e10 0116 .........-. ....
00000110: 1024 1e01 1f1a 011a 1b10 1900 0f1a 1a1d .$..............
00000120: 1e2d 0000Однако результаты ничем не примечательны. Разумеется, получившийся поток данных стал более развёрнутым по сравнению с исходным, но ненамного. Определённо не настолько, чтобы содержать в себе все данные, которые мы ожидаем найти. Очевидно, что эта схема распаковки немного проще, чем нужно.
Если внимательнее изучить полученный вывод, то мы вскоре увидим, что он начинается со множества повторяющихся байтов. 0b, 04, 00, 0a — все они встречаются попарно. Взглянув на сжатый оригинал, мы увидим, что все эти пары возникли из-за замены по словарю. Но в процессе мы сразу же заметим, что все эти повторяющиеся значения также соответствуют записям в словаре. То есть если мы снова применим словарь, то данные снова расширятся. Возможно, мы недостаточно распаковываем?
Нашей первой догадкой может стать выполнение второго прохода, применение каждой записи словаря второй раз, чтобы развернуть данные ещё больше. Второй догадкой может быть выполнение многократных проходов со словарём, повторение процесса, пока не будут заменены все байты, похожие на ключи словаря. Однако если мы внимательнее приглядимся к структуре словаря, то осознаем, что мы просто применяем записи словаря справа налево, а не слева направо, когда все наши значения будут развёрнуты за один проход.
Взяв эту гипотезу, мы можем увидеть структуру более правдоподобного алгоритма сжатия. Программа берёт исходные данные и сканирует их, ища самые часто встречающиеся двухбайтные последовательности. Затем она заменяет двухбайтную последовательность одним байтовым значением, которое не встречается в данных. Затем она повторяет процесс, продолжая его, пока в данных не найдётся более чем двукратного повторения двухбайтных последовательностей. На самом деле, у такого алгоритма сжатия есть название: он известен как сжатие «re-pair», что является сокращением от «recursive pairs».
(И это может объяснить некоторые паттерны, которые мы видим в словаре. В процессе сжатия словарь строится слева направо, поэтому при распаковке он должен применяться справа налево. Так как записи словаря часто ссылаются на предыдущие записи, логично, что вторые и третьи байты часто будут меньше по значению, чем первый.)
Хотя сжатие re-pair даёт не особо впечатляющие результаты, оно имеет преимущество: распаковщик можно реализовать минимумом кода. Я и сам использовал re-pair в некоторых ситуациях, когда мне нужно было минимизировать общий размер сжатых данных и кода распаковки.
Итак, мы можем внести изменение в одну строку программы на Python, чтобы применять словарь справа налево:
Файл decompress2.py:
import struct
import sys
# Read the compressed data file.
data = sys.stdin.read()
# Extract the two integers of the four-byte header.
tablesize, datasize = struct.unpack('HH', data[0:4])
data = data[4:]
# Separate the dictionary table and the compressed data.
tablesize *= 3
table = data[0:tablesize]
data = data[tablesize:datasize]
# Apply the dictionary entries to the data section in reverse order.
for n in range(len(table) - 3, -3, -3):
key = table[n]
val = table[n+1:n+3]
data = data.replace(key, val)
# Output the expanded result.
sys.stdout.write(data)
Если мы попробуем эту версию, то вывод будет гораздо больше:
$ python ./decompress2.py <levels/lesson_1.pak | xxd | less 00000000: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000010: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000020: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000030: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000040: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000050: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000060: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000070: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000080: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000090: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 000000a0: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 000000b0: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 000000c0: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 000000d0: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 000000e0: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 000000f0: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000100: 0000 0000 0000 0000 0000 0101 0101 0100 ................ 00000110: 0101 0101 0100 0000 0000 0000 0000 0000 ................ 00000120: 0000 0000 0000 0000 0000 0100 0000 0101 ................ 00000130: 0100 0000 0100 0000 0000 0000 0000 0000 ................ 00000140: 0000 0000 0000 0000 0000 0100 2300 0125 ............#..% 00000150: 0100 2300 0100 0000 0000 0000 0000 0000 ..#............. 00000160: 0000 0000 0000 0000 0101 0101 011d 0124 ...............$ 00000170: 011d 0101 0101 0100 0000 0000 0000 0000 ................ lines 1-24/93 (more)
Мы видим в этом выводе много нулевых байтов, но это вполне может соответствовать почти пустой карте. Похоже, ненулевые байты сгруппировались рядом друг с другом. Так как мы надеемся найти карту размером 32 × 32, давайте переформатируем вывод в 32 байт на строку:
$ python ./decompress2.py <levels/lesson_1.pak | xxd -c32 | less 00000000: 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 ................................ 00000020: 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 ................................ 00000040: 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 ................................ 00000060: 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 ................................ 00000080: 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 ................................ 000000a0: 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 ................................ 000000c0: 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 ................................ 000000e0: 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 ................................ 00000100: 0000 0000 0000 0000 0000 0101 0101 0100 0101 0101 0100 0000 0000 0000 0000 0000 ................................ 00000120: 0000 0000 0000 0000 0000 0100 0000 0101 0100 0000 0100 0000 0000 0000 0000 0000 ................................ 00000140: 0000 0000 0000 0000 0000 0100 2300 0125 0100 2300 0100 0000 0000 0000 0000 0000 ............#..%..#............. 00000160: 0000 0000 0000 0000 0101 0101 011d 0124 011d 0101 0101 0100 0000 0000 0000 0000 ...............$................ 00000180: 0000 0000 0000 0000 0100 2000 1b00 0000 0000 1a00 2000 0100 0000 0000 0000 0000 .......... ......... ........... 000001a0: 0000 0000 0000 0000 0100 2300 011f 0033 001e 0100 2300 0100 0000 0000 0000 0000 ..........#....3....#........... 000001c0: 0000 0000 0000 0000 0101 0101 0123 0000 0023 0101 0101 0100 0000 0000 0000 0000 .............#...#.............. 000001e0: 0000 0000 0000 0000 0100 2300 011f 0000 001e 0100 2300 0100 0000 0000 0000 0000 ..........#.........#........... 00000200: 0000 0000 0000 0000 0100 0000 1a00 0023 0000 1b00 0000 0100 0000 0000 0000 0000 ...............#................ 00000220: 0000 0000 0000 0000 0101 0101 0101 1c01 1c01 0101 0101 0100 0000 0000 0000 0000 ................................ 00000240: 0000 0000 0000 0000 0000 0000 0100 0001 0000 0100 0000 0000 0000 0000 0000 0000 ................................ 00000260: 0000 0000 0000 0000 0000 0000 0100 2301 2300 0100 0000 0000 0000 0000 0000 0000 ..............#.#............... 00000280: 0000 0000 0000 0000 0000 0000 0100 0001 2100 0100 0000 0000 0000 0000 0000 0000 ................!............... 000002a0: 0000 0000 0000 0000 0000 0000 0101 0101 0101 0100 0000 0000 0000 0000 0000 0000 ................................ 000002c0: 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 ................................ 000002e0: 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 ................................ lines 1-24/47 (more)
Внимательно посмотрев на паттерны ненулевых значений, мы увидим, что в выводе чётко видна карта. На самом деле, мы можем сделать этот паттерн более заметным с помощью инструмента «раскрашенного» дампа, который назначает каждому байтовому значению свой цвет, упрощая поиск паттернов повторяющихся значений:
xcd — это нестандартный инструмент, но его можно скачать отсюда. Заметьте опцию -r утилиты less, которая приказывает очищать управляющие последовательности.
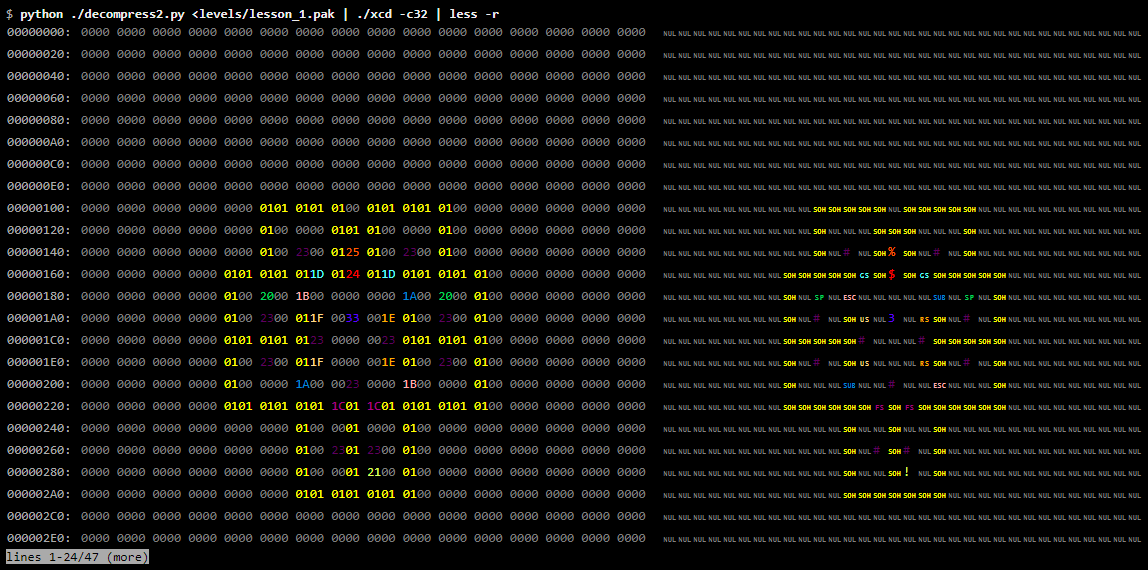
Сравните это с нарисованной фанатами картой первого уровня:

Без сомнений, мы видим данные карты уровня. Можно быть вполне уверенными, что мы верно определили алгоритм распаковки.
Интерпретирование данных
Сравнивая байтовые значения с изображением карты, мы можем определить, что
00 кодирует пустой тайл, 01 кодирует стену, а 23 обозначает чип. 1A обозначает красную дверь, 1B — синюю дверь, и так далее. Мы можем присвоить точные значения чипам, ключам, дверям и всем другим тайлам, из которых состоит вся карта уровня.
Теперь мы можем перейти на следующий уровень и найти байтовые значения для появляющихся там объектов. И продолжить со следующими уровнями, пока не получим полный список байтовых значений и игровых объектов, которые они кодируют.
Как мы изначально и предположили, карта заканчивается ровно после 1024 байт (по смещению 000003FF).
На этот раз для удаления первых 32 строк дампа мы используем sed. Поскольку у нас отображается по 32 байта на строку, так мы пропустим первые 1024 байт.
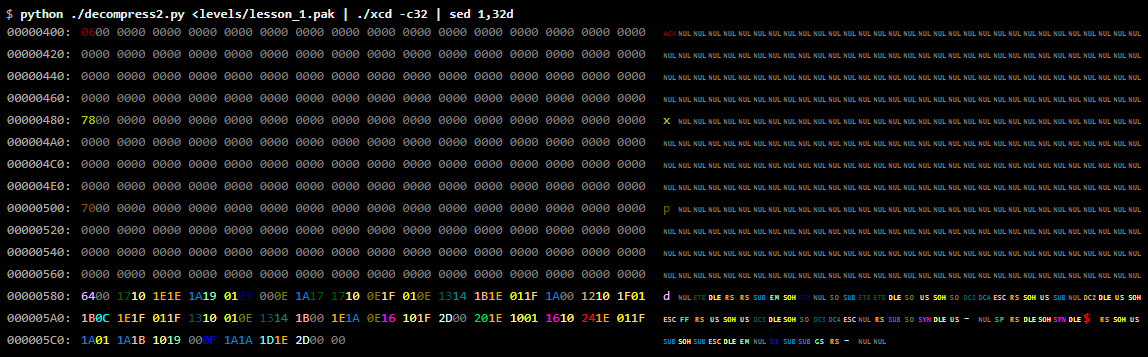
Сразу же за данными карты идёт последовательность из 384 байт (значения которых находятся в интервале
00000400–0000057F), почти все из которых равны нулю, но между ними попадаются и ненулевые значения. После этого идёт совершенно другой паттерн байтов, поэтому логично будет предположить, что эта 384-байтная последовательность является отдельной частью.
Если мы посмотрим ещё на несколько уровней, то быстро заметим паттерн. 384-байтная часть на самом деле состоит из трёх подразделов, каждый длиной 128 байт. Каждый подраздел начинается с нескольких ненулевых байтов, за которым идут нули, заполняющие остаток подраздела.
У некоторых уровней здесь содержится много данных; у других (например у первого уровня) только самый минимум. Сравнивая уровни с их картами, мы вскоре заметим, что количество данных в этой части файла напрямую связано с количеством «мобов» на уровне. В данном случае в число «мобов» включаются все существа на уровне, блоки земли (которые не движутся самостоятельно, но их можно толкать) и сам главный герой Чип (игрок). То есть мобы указываются не на самой карте, а кодируются в этих трёх буферах.
После того, как мы узнали, что в этих трёх подразделах содержатся данные о мобах на уровне, будет не очень сложно разобраться, что же содержится в каждом из подразделов.
Первый 128-байтный подраздел — это список байтовых значений, определяющих тип моба. Например, буферы второго уровня выглядят так:
$ python ./decompress2.py <levels/lesson_2.pak | xxd | less 00000400: 0608 1c1c 0808 0000 0000 0000 0000 0000 ................ 00000410: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000420: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000430: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000440: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000450: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000460: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000470: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000480: a870 98a0 6868 0000 0000 0000 0000 0000 .p..hh.......... 00000490: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 000004a0: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 000004b0: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 000004c0: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 000004d0: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 000004e0: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 000004f0: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000500: 6060 6060 5868 0000 0000 0000 0000 0000 ````Xh.......... 00000510: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000520: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000530: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000540: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000550: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000560: 0000 0000 0000 0000 0000 0000 0000 0000 ................ 00000570: 0000 0000 0000 0000 0000 0000 0000 0000 ................ lines 64-87/93 (more)
Сравните это с картой уровня:

На этом уровне содержится шесть мобов: три жука, два блока и Чип. Первый 128-байтный подраздел содержит один байт
06, три байта 08 и два байта 1C. Разумно будет заключить, что 06 обозначает Чипа, 08 — жука, а 1C — блок.
(Продолжив сравнивать файлы данных с картами уровней и заполнять наш словарь мобов, мы быстро найдём в этой теории изъян: Чип может быть обозначен четырьмя разными значениями, а именно 04, 05, 06 или 07. Это множество обозначений на самом деле содержит всех мобов. При внимательном изучении разных значений мы со временем поймём, что к байтовому значению, обозначающему тип, прибавляется значение 0, 1, 2 или 3, обозначающее первоначальное направление моба: север, восток, юг или запад. То есть, например, байтовое значение 06 обозначает Чипа, смотрящего на юг.)
Значение двух других подразделов менее очевидно. Но изучив повторяющиеся значения в этих подразделах и сравнив карты для этих мобов, мы поймём, что байты во втором подразделе хранят координату X каждого моба, а байты в третьем подразделе — координату Y каждого моба. Пониманию этого решения мешает тот факт, что координаты, хранящиеся в этих подразделах, на самом деле сдвинуты на 3 бита влево, т.е. умножены на 8. Этот небольшой факт объясняет «синюю» группу, которую мы обнаружили при переписи значений. (Причины, по которым выполнен этот сдвиг, непонятны, но скорее всего нижние три бита используются для представления анимации, когда мобы двигаются.)
Разобравшись с этой частью, мы можем теперь увидеть, у скольких файлов данных осталось после неё всего несколько байт:
Учтите, что xxd принимает для опции -s шестнадцатеричное значение.
$ for f in levels/* ; do python ./decompress2.py <$f | xxd -s 0x580 | sed -n 1p ; done | less 00000580: 9001 0c17 1701 1120 1717 00 ....... ... 00000580: 0000 0c17 1b13 0c0d 101f 011e 1a20 1b00 ............. .. 00000580: f401 0c18 1e1f 101d 0f0c 1800 ............ 00000580: 2c01 0c1b 0c1d 1f18 1019 1f00 ,........... 00000580: 9001 0c1d 0e1f 140e 1117 1a22 00 ...........". 00000580: 2c01 0d0c 1717 1e01 1a01 1114 1d10 00 ,.............. 00000580: 2c01 0d10 220c 1d10 011a 1101 0d20 1200 ,..."........ .. 00000580: 5802 0d17 1419 1600 X....... 00000580: 0000 0d17 1a0d 0f0c 190e 1000 ............ 00000580: f401 0d17 1a0d 1910 1f00 .......... 00000580: f401 0d17 1a0e 1601 110c 0e1f 1a1d 2400 ..............$. 00000580: ee02 0d17 1a0e 1601 0d20 1e1f 101d 0114 ......... ...... 00000580: 5802 0d17 1a0e 1601 1901 1d1a 1717 00 X.............. 00000580: 5e01 0d17 1a0e 1601 1a20 1f00 ^........ .. 00000580: c201 0d17 1a0e 1601 0d20 1e1f 101d 00 ......... ..... 00000580: 2c01 0d1a 2019 0e10 010e 141f 2400 ,... .......$. 00000580: 5000 0d1d 201e 1311 141d 1000 P... ....... 00000580: e703 0e0c 1610 0122 0c17 1600 .......".... 00000580: 5802 0e0c 1e1f 1710 0118 1a0c 1f00 X............. 00000580: 8f01 0e0c 1f0c 0e1a 180d 1e00 ............ 00000580: 0000 0e10 1717 0d17 1a0e 1610 0f00 1b1d ................ 00000580: 2c01 0e13 0e13 0e13 141b 1e00 ,........... 00000580: 8f01 0e13 1417 1710 1d00 .......... 00000580: bc02 0e13 141b 1814 1910 00 ........... lines 1-24/148 (more)
Изучение первой пары байтов в оставшейся части быстро намекает нам, что они содержат ещё одно 16-битное целочисленное значение. Если считать их так, то большинство значений оказывается в десятичной записи круглыми числами:
Команда od для перехода к исходному смещению использует -j вместо -s. Также стоит заметить команду printf: кроме обеспечения форматирования, она является удобным способом вывода текста без висящего в конце символа новой строки.
$ for f in levels/* ; do printf "%-20s" $f ; python ./decompress2.py <$f | od -An -j 0x580 -tuS -N2 ; done | less levels/all_full.pak 400 levels/alphabet.pak 0 levels/amsterda.pak 500 levels/apartmen.pak 300 levels/arcticfl.pak 400 levels/balls_o_.pak 300 levels/beware_o.pak 300 levels/blink.pak 600 levels/blobdanc.pak 0 levels/blobnet.pak 500 levels/block_fa.pak 500 levels/block_ii.pak 750 levels/block_n_.pak 600 levels/block_ou.pak 350 levels/block.pak 450 levels/bounce_c.pak 300 levels/brushfir.pak 80 levels/cake_wal.pak 999 levels/castle_m.pak 600 levels/catacomb.pak 399 levels/cellbloc.pak 0 levels/chchchip.pak 300 levels/chiller.pak 399 levels/chipmine.pak 700 lines 1-24/148 (more)
Если мы снова обратимся к списку, изначально созданному из данных, которые ожидали найти в файлах, то осознаем, что это число — время на прохождение уровня (если значение равно нулю, то на уровне нет ограничения по времени).
После этих двух байтов данные становятся более изменчивыми. Тот факт, что для большинства уровней в файле остаётся примерно по десятку байт, серьёзно ограничивает их содержимое:
$ python ./decompress2.py <levels/all_full.pak | xxd -s 0x0582 00000582: 0c17 1701 1120 1717 00 ..... ...
Например, в этом уровне остаётся всего девять байтов. Учтём этот ограниченный размер, а также тот факт, что эти девять байт содержат четыре вхождения значения
17, собранных в две пары. Мы сразу же заметим, что паттерн из чисел 17 соответствует паттерну букв L в названии уровня «ALL FULL». Название имеет длину восемь символов, так что нулевой байт в конце скорее всего является символом конца строки. Обнаружив это, можно тривиальным образом просмотреть все другие уровни и использовать их названия для сборки полного списка символов:
00 |
конец строки |
01 |
пробел |
02–0B |
цифры 0-9 |
0C–25 |
буквы A-Z |
26–30 |
знаки препинания |
Для большинства уровней файл данных на этом заканчивается. Однако у пары десятков за названием ещё есть данные. Если мы взглянем на список, то увидим, что есть уровни с кнопками подсказок, и эти оставшиеся данные содержат текст строки подсказки уровня, закодированный тем же набором символов, что и названия уровней.
После этого мы достигли конца всех файлов. Теперь у нас есть полное описание схемы данных уровней. Наша задача выполнена.
Незавершённые дела
Внимательный читатель может заметить, что изначально мы ожидали найти в этих файлах ещё два элемента, которые так ни разу и не встретили. Мы объясним отсутствие обоих:
Первый элемент — это количество чипов, т.е. общее число чипов, которые должен собрать игрок, чтобы пройти через разъём чипа. Как мы говорили изначально, часто оно равно общему количеству чипов на уровне, но так бывает не всегда. Поэтому эти данные каким-то образом нужно получать. Ответ можно найти, изучив карты тех уровней, на которых есть лишние чипы. Оказывается, что для обозначения чипов используется два разных значения. Значение 23 мы обнаружили изначально, но также используется значение 31, обозначающее чип, который не влияет на общее количество, необходимое для открытия разъёма чипа. (Однако, с точки зрения геймплея оба типа чипа одинаковы. Если на уровне есть один чип типа 31, то на уровне можно не собирать любое количество чипов.)
Второй элемент — это четырёхбуквенный пароль уровня. Он не скрыт нигде в данных уровня. К сожалению, этот задачу не решить дальнейшим исследованием файла данных. Мы вынуждены заключить, что пароли просто хранятся где-то в другом месте. Самое вероятное объяснение: они жёстко прописаны где-то в самой программе. Однако позже выяснилось, что пароли не хранятся напрямую. От людей, знакомых с самим кодом, я узнал, что пароли генерируются динамически с помощью генератора псевдослучайных чисел, инициализируемого определённой последовательностью. Следовательно, пароли к уровням невозможно изменять напрямую, это можно сделать только изменением ассемблерного кода.
Послесловие
Выполнив полный реверс-инжиниринг данных в файлах уровней, я мог начать писать программу, способную кодировать и декодировать данные уровней. Благодаря ей я смог создать долгожданный редактор уровней для версии Chip's Challenge под Lynx, и наличие этого инструмента сильно повысило мои возможности по изучению логики игры, а также улучшило качество её эмуляции.
Но… должен признаться, что лично я выполнял обратную разработку файлов данных не в описанном выше порядке. Я начал с другого конца — с определения строковых данных. Я принялся изучать файлы первых восьми уровней. Так как они называются с «LESSON 1» по «LESSON 8», я искал в них данные одинаковых подстрок. И мне повезло: ни одно из названий этих уровней не подверглось сжатию, поэтому все восемь названий хранятся в файлах данных в исходном виде. Разумеется, меня смутило, что эти строки хранятся не в символах ASCII, но двойная S в названии помогла мне обнаружить паттерн, повторяющийся во всех восьми файлов данных. А найдя название, я узнал кодировку символов букв, цифр и символа пробела. Затем я применил это кодирование к остальной части файла и сразу после названия увидел строки подсказок, и начал наблюдать аномалии:
Великолепная утилита tr упрощает преобразование собственного набора символов файлов данных в ASCII.
$ tr '\001-\045' ' 0-9A-Z' <levels/lesson_1.pak | xxd 00000000: 4600 cb00 3000 0032 3030 3332 3235 3333 F...0..200322533 00000010: 3635 3537 0020 3820 2039 3636 4238 3846 6557. 8 966B88F 00000020: 0058 4a37 354d 3000 5737 4226 3746 2739 .XJ75M0.W7B&7F'9 00000030: 3928 3533 2953 2027 2733 3042 2057 3532 9(53)S ''30B W52 00000040: 3730 3738 304a 3226 375a 2046 4a30 5752 70780J2&7Z FJ0WR 00000050: 2059 2052 4220 3537 0055 0050 3200 4f00 Y RB 57.U.P2.O. 00000060: 554a 2637 5400 3300 2946 4a57 5830 4642 UJ&7T.3.)FJWX0FB 00000070: 2035 2637 544d 2946 4a37 4d4f 3058 3050 5&7TM)FJ7MO0X0P 00000080: 304a 5720 5120 5142 3835 3237 3020 3020 0JW Q QB85270 0 00000090: 2826 2058 4a33 3730 2056 4a33 5738 2727 (& XJ370 VJ3W8'' 000000a0: 3933 3200 3439 3628 324d 7839 3628 324d 932.496(2Mx96(2M 000000b0: 7039 3628 324d 6400 4c45 5353 4f4e 2031 p96(2Md.LESSON 1 000000c0: 0043 4f4c 4c45 4354 2043 4849 5029 544f .COLLECT CHIP)TO 000000d0: 0047 4554 2050 4153 5420 5448 4520 4348 .GET PAST THE CH 000000e0: 4950 0053 4f43 4b45 542d 0055 5345 204b IP.SOCKET-.USE K 000000f0: 4559 2954 4f20 4f50 454e 0044 4f4f 5253 EY)TO OPEN.DOORS 00000100: 2d30 -0
Например, в тексте подсказки есть два места, где последовательность из S и пробела заменена на правую скобку. Эти аномалии дали мне достаточно улик, чтобы дедуктивно вычислить наличие сжатия и получить некую информацию о её природе. Позже я связал аномальные байтовые значения с их вхождениями ближе к началу файла данных. (Например, в показанном выше шестнадцатеричном дампе по смещению
00000035 есть правая скобка, за которой следует заглавная S и пробел.) Из этого я вычислил схему сжатия аналогично описанному в статье процессу. Всё остальное было довольно просто.
Мне кажется, из этого можно извлечь такой урок: нет единственно верного способа исследования незнакомого файла данных. Любые инструменты, которые подойдут вам — это подходящие инструменты для реверс-инжиниринга.
Комментариев нет:
Отправить комментарий