[Перевод] Как квантовые вычисления могут повлиять на разработку ПО

Всем привет!

Примерно в течение последнего полугода издательство активно прорабатывает тему квантовых вычислений и их практической применимости. Долго не удавалось найти достойную статью для перевода по этой интереснейшей теме, пока такая статья не появилась в блоге Oracle. Публикация послужит отличным введением и в программные, и в аппаратные, и в сугубо естественнонаучные проблемы этой новой парадигмы, поэтому — читать обязательно.

В течение последних месяцев и лет значительно возрос интерес к квантовым вычислениям. Постоянно появляются новые материалы из исследовательских институтов, компаний или государственных организаций, рассказывающие о прорывных достижениях в этой сфере. В то же время, в статьях с более слабым техническим базисом рассуждают о потенциальных последствиях квантовых вычислений, причем, прогнозы варьируются от взлома большинства современных приемов шифрования до обещаний об излечении всех болезней и завершения работы над созданием полноценного ИИ. Однако, не все эти ожидания одинаково реалистичны.

Если вы – практикующий трезвомыслящий программист, то вам, должно быть, интересно, где граница между фактами и вымыслами в этих выкладках, и как квантовые вычисления повлияют на разработку ПО в будущем.

Естественно, остается еще много лет до создания рабочего аппаратного обеспечения для квантовых вычислений. Однако, общие принципы этой парадигмы понятны уже сегодня, существуют абстракции, позволяющие разработчикам создавать приложения, в которых возможности квантовых вычислений реализуются при помощи симуляторов.

Не сводятся ли квантовые вычисления к очередному усилению CPU?

Традиционная разработка ПО с использованием классических компьютеров, связана с трансляцией высокоуровневого языка программирования (например, Java) в операции, совершаемые на большом количестве (аппаратных) транзисторов.

На рисунке 1 этот процесс схематизирован в простейшем виде: исходный код Java компилируется в платформонезависимый байт-код, который, в свою очередь, транслируется в платформоспецифичный машинный код. Машинный код использует ряд простейших операций (вентилей), выполняемых в памяти. Основной аппаратный компонент, используемый для этой цели – всем известный транзистор.

Рис. 1. Трансляция высокоуровневого языка программирования в операции, выполняемые на транзисторах.

Увеличение производительности, полученное в последние годы, было достигнуто в основном благодаря совершенствованию аппаратных технологий. Размеры отдельно взятого транзистора радикально уменьшились, а чем больше транзисторов удается уложить на каждый квадратный миллиметр – тем больше памяти и вычислительной мощности будет у компьютера.

Квантовые вычисления – это подрывная технология, так как здесь в качестве простейших вычислительных единиц используются не классические транзисторы, а кубиты, о которых мы поговорим чуть ниже.

Дело не только в отличиях этих первоэлементов, но и в ином устройстве вентилей. Таким образом, стек с рис. 1 в квантовых вычислениях неприменим.

Разрушат ли квантовые вычисления весь вышеуказанный стек вплоть до уровня Java?

Если коротко – «не совсем». Ученые постепенно приходят к согласию в том, что квантовые компьютеры будут особенно хороши для решения специфических задач, в то время как другие задачи рациональнее будет решать при помощи традиционных компьютеров. Звучит знакомо, правда? Аналогичная ситуация наблюдается при сравнении GPU и CPU. Тогда как в GPU также используются транзисторы, по принципу работы они отличаются от CPU.Однако, многие приложения, написанные на высокоуровневом языке, под капотом используют возможности как CPU, так и GPU. GPU очень хороши для векторной обработки, и во многих приложениях и библиотеках работа CPU и GPU разграничивается.

Например, именно такая ситуация возникает при использовании JavaFX или Deeplearning4j. Если вы пишете при помощи JavaFX приложение с пользовательским интерфейсом, то работаете только с кодом на Java (еще, может быть, с FXML для объявления пользовательского интерфейса). Когда сцену JavaFX требуется отобразить на экране, внутренние реализации JavaFX используют для этого шейдеры и текстуры, напрямую контактируя с низкоуровневыми драйверами GPU, как показано на рисунке 2. Поэтому вам не приходится беспокоиться, какая часть кода лучше приспособлена для работы с CPU, а какая – с GPU.

Рис. 2. JavaFX делегирует работу GPU и CPU.

Как показано на рис. 2, код реализации JavaFX делегирует работу, передавая ее GPU и CPU. Хотя, от разработчика эти операции скрыты (не предоставляются через API), определенные знания о GPU зачастую полезны, когда требуется разрабатывать более производительные приложения JavaFX.

При использовании Deeplearning4j складывается схожая ситуация. В Deeplearning4j есть ряд реализаций для выполнения требуемых векторных и матричных операций, и при некоторых из них используются GPU. Однако, вам как конечному разработчику не важно, какие именно мощности будет использовать ваш код — CPU или GPU.

Представляется, что квантовые компьютеры будут отлично справляться с решением задач, которые, как правило, наращиваются экспоненциально по мере роста объемов задачи и, поэтому, с трудом решаемы или почти нерешаемы с использованием классических компьютеров. В частности, эксперты рассуждают о гибридном варианте выполнения: типичное сквозное приложение содержит классический код, выполняемый на CPU, но в нем также может присутствовать и квантовый код.

Как система может выполнять квантовый код?

Сегодня аппаратное обеспечение для квантовых компьютеров по-прежнему остается крайне экспериментальным. Тогда как крупные корпорации и, предположительно, некоторые государства занимаются разработкой прототипов, в широком доступе такой техники нет. Но, когда она появится, форма ее может быть разной:

• Квантовый сопроцессор можно интегрировать с CPU в системе.
• Квантовые задачи можно делегировать квантовым облачным системам.

Хотя, сохраняется огромная неопределенность по поводу практической подоплеки таких решений, мы приходим все к большему согласию о том, как должен выглядеть квантовый код. На самом низком уровне должны находиться следующие кирпичики: кубиты и квантовые вентили. На их основе можно создавать квантовые симуляторы, реализующие ожидаемое поведение.

Следовательно, квантовый симулятор – идеальный инструмент для подобной разработки.
Выдаваемые им результаты должны быть практически такими же, какие были бы получены на реальном оборудовании квантового компьютера – но симулятор работает гораздо медленнее, так как квантовые эффекты, ускоряющие квантовое оборудование, приходится имитировать при помощи традиционного ПО.

Каков основные строительные блоки квантовых вычислений?

Часто бывает важно сравнить классические вычисления с квантовыми. В классических вычислениях у нас есть биты и вентили.

Бит содержит единственный разряд информации, и его значение может быть равно 0 или 1.
Вентиль действует на один или более бит и может оперировать ими. Например, вентиль NOT, показанный на рисунке 3, меняет значение бита на противоположное. Если ввод равен 0, то вывод вентиля NOT будет равен 1 и наоборот.

Рис. 3. Вентиль NOT

В квантовых вычислениях у нас есть эквиваленты битов и вентилей. Квантовый эквивалент бита – кубит. Значение кубита может быть равно 0 или 1, как и у классического бита, однако, может находиться и в так называемой суперпозиции. Это сложнопредставимая концепция, согласно которой кубит может одновременно находиться в обоих состояниях: 0 и 1.
Когда кубит находится в суперпозиции, его значение является линейной комбинацией состояний 0 и 1. Это можно записать как показано на рис. 4:

Рис. 4. Равенство, где кубит находится в суперпозиции.

Обратите внимание: кубиты зачастую записываются в нотации бра-кет, где имя переменной ставится между символами "|" и ">".

Выражение на рис. 4 сообщает, что кубит x находится в суперпозиции состояний |0> и |1>. Это не означает, что он находится в состоянии |0> ИЛИ в состоянии |1>; это означает, что его текущее состояние нам не известно.

На самом деле, он находится в обоих состояниях одновременно, и в таком виде им можно манипулировать. Однако, когда мы измерим кубит, он окажется в одном состоянии, либо |0>, либо |1>. В вышеприведенном выражении существует и другое ограничение: a^2 + b^2 = 1.
Значения a и b являются вероятностными: существует вероятность a^2, что, когда мы измерим кубит |x>, в нем будет значение |0>, и вероятность b^2, что измеренный кубит будет содержать значение |1>.

Есть важный ограничивающий фактор, обламывающий радости квантовых вычислений: после того, как кубит измерен, теряется вся информация о потенциальной суперпозиции, в которой он находился. Значение кубита может быть равно 0 или 1.

При вычислениях кубит в суперпозиции может соответствовать одновременно 0 и 1 (с разными вероятностями). Если у нас два кубита, то с их помощью можно представить четыре состояния (00, 01, 10 и 11), опять же, с разными вероятностями. Здесь мы подходим к сути всей мощи квантовых компьютеров. Имея восемь классических бит, можно представить ровно одно число в диапазоне от 0 до 255. Значения каждого из восьми бит будут равны 0 или 1. Имея восемь кубит, можно одновременно представить все числа от 0 до 255.

В чем польза суперпозиции, если измерить можно всего одно состояние?

Зачастую результат алгоритма прост («да» или «нет»), но, чтобы прийти к нему, требуется масса параллельных вычислений. Удерживая кубиты в суперпозиции при вычислениях, можно сразу учесть любое множество различных вариантов. Не выполняя решения для каждой отдельной комбинации, квантовый компьютер может высчитать все варианты за один шаг.
Затем во многих квантовых алгоритмах наступает следующий важный этап: связать итог алгоритма с измерением, дающим осмысленный результат. Зачастую при этом учитывается интерференция: интересные результаты конструктивно накладываются друг на друга, а неинтересные гасят друг друга (деструктивная интерференция).

Как можно «преобразовать» кубит в состояние суперпозиции?

Подобно тому, как классические вентили манипулируют битами, квантовые вентили манипулируют кубитами. Некоторые квантовые вентили напоминают классические; например, вентиль Pauli-X переводит кубит из состояния a|0> + b|1> в состояние b|0| + a|1>, что похоже на принцип работы классического вентиля NOT. Действительно, когда a = 1 и b = 0, кубит исходно находился в состоянии |0>. После воздействия вентиля Pauli-X этот кубит перейдет в состояние |1>, как показано на рис. 5.

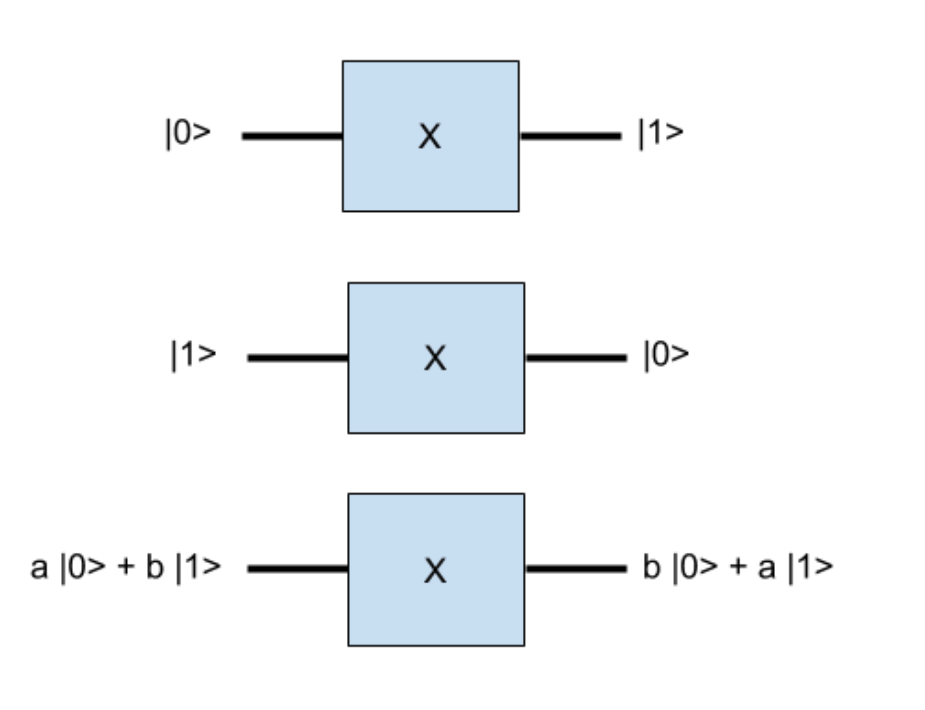
Рис. 5. Результат применения вентиля Pauli-X.

В данном контексте очень интересен вентиль Адамара. Он переводит в суперпозицию кубит, находившийся в состоянии |0>: 1/sqrt(2)* (|0> + |1>), как показано на рис. 6.

Рис. 6. Результат применения вентиля Адамара.

После того, как мы применим к кубиту вентиль Адамара и измерим кубит, существует 50% вероятность, что значение кубита будет равно 0 и 50% — что значение кубита будет равно 1. До тех пор, пока кубит не измерен, он остается в состоянии суперпозиции.

Как все это возможно?

Если вас действительно интересует ответ на этот вопрос – придется подробно изучить квантовую физику. Но, к счастью, всю теоретическую основу этих явлений понимать не требуется. Притом, что феномен суперпозиции может казаться непостижимым, важно подчеркнуть, что именно такие свойства характерны для элементарных частиц в природе. Следовательно, квантовые вычисления гораздо ближе к основам физической реальности, чем кажется на первый взгляд.

Стоит ли подождать несколько лет, а потом уже присматриваться к квантовым вычислениям?

Нет. В таком случае вы опоздаете. Теоретически возможно сначала разработать аппаратное обеспечение, а затем перейти к исследованию программного уровня и посмотреть, чего можно достичь с его помощью. Однако, все концепции уже более-менее ясны, и уже можно писать квантовые симуляторы на популярных языках, в том числе, на Java, C#, Python и других.
Затем эти симуляторы могут применяться для работы над квантовыми алгоритмами. Хотя, эти алгоритмы и не дадут такого роста производительности, который достижим с их помощью при работе на реальном квантовом оборудовании, функционально они должны получиться совершенно полноценными.

Таким образом, если вы сейчас разрабатываете квантовый алгоритм, то у вас есть время на его совершенствование, а запустить его сможете, когда в доступе появится квантовое оборудование.

Квантовые алгоритмы требуют иного интеллектуального подхода, нежели классические. Выдающиеся ученые приступили к разработке квантовых алгоритмов еще в прошлом веке, а сейчас публикуется все больше статей с описанием таких алгоритмов, в том числе, для перемножения целых чисел, поиска по спискам, работы над оптимизацией путей и многого другого.

Есть и другие причины, по которым, возможно, стоит заняться квантовыми вычислениями уже сегодня. Рефакторинг софтверной системы в современной большой компании – не из тех дел, какие можно провернуть за ночь. Однако, одна из областей, в которых квантовые вычисления произведут настоящий переворот – это шифрование; ведь все оно основано на теории, что на классическом компьютере практически невозможно разложить большое целое число на простые множители.

Хотя, могут пройти многие годы, прежде чем квантовые компьютеры станут достаточно велики, чтобы легко решать задачу целочисленной факторизации, разработчики знают, что много лет уходит и на изменение систем, и на внедрение в них новых, более безопасных технологий.

Как можно научиться работать с квантовыми алгоритмами на Java?

Можно скачать и освоить Strange, опенсорсный симулятор квантового компьютера на Java. Strange позволяет смоделировать квантовый алгоритм, создав ряд кубитов и применив к ним несколько квантовых вентилей.

В качестве простейшего примера давайте создадим два кубита, q[0] и q[1], так, что исходно оба они находятся в состоянии 0. Затем применим к каждому из кубитов по два простых вентиля, так, чтобы графически эта операция соответствовала рис. 7.

Первый кубит сначала попадет на вентиль Pauli-X, а затем на вентиль Адамара. Вентиль Pauli-X переведет его из состояния |0&gt к |1&gt, а вентиль Адамара переведет в суперпозицию с равными вероятностями |0&gt и |1&gt. Следовательно, если мы выполним всю последовательность 1000 раз, и 1000 раз измерим первый кубит в конце этого цикла, то в среднем можно ожидать, что в 500 случаях у него будет значение 0 и в 500 случаях – значение 1.

Второй кубит даже проще. Начинаем с вентиля Identity, который не меняет поведения кубита, после чего передаем его на вентиль Pauli-X, меняющий его значение с 0 на 1.

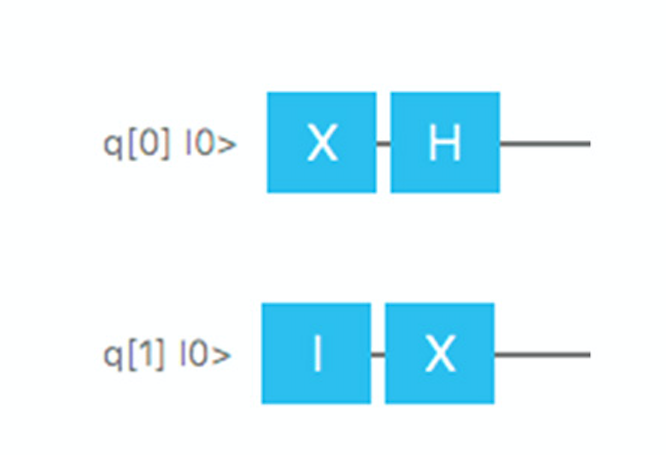
Рис. 7. Пример квантового алгоритма, который можно сымитировать при помощи Strange.

Чтобы убедиться в верности наших рассуждений, можно создать простую квантовую программу при помощи Strange.

public static void main(String[] args) {
        Program p = new Program(2);
        Step s = new Step();
        s.addGate(new X(0));
        p.addStep(s);
        Step t = new Step();
        t.addGate(new Hadamard(0));
        t.addGate(new X(1));
        p.addStep(t);
        SimpleQuantumExecutionEnvironment sqee = new SimpleQuantumExecutionEnvironment();
        Result res = sqee.runProgram(p);
        Qubit[] qubits = res.getQubits();
        Arrays.asList(qubits).forEach(q -> System.out.println("qubit with probability on 1 = "+q.getProbability()+", measured it gives "+ q.measure()));
    }

В этом приложении создается квантовая программа с двумя кубитами:

    Program p = new Program(2);

В рамках этой программы проходим два этапа. На первом этапе применяем вентиль Pauli-X к q[0]. Мы не применяем вентиль к q[1], и таким образом подразумеваем, что он будет работать с вентилем Identity. Добавляем этот этап в программу:

       Step s = new Step();
        s.addGate(new X(0));
        p.addStep(s);

Затем переходим ко второму этапу, где применяем вентиль Адамара к q[0] и вентиль Pauli-X к q[1]; добавляем в программу и этот шаг:

    Step t = new Step();
        t.addGate(new Hadamard(0));
        t.addGate(new X(1));
        p.addStep(t);

Итак, наша программа готова. Теперь давайте ее выполним. В Strange встроен квантовый симулятор, однако, Strange также може использовать облачный сервис для выполнения программ в каком-нибудь облаке, например, в Oracle Cloud.

В следующем примере мы используем простой встроенный симулятор, запускаем программу и получаем результирующие кубиты:

 SimpleQuantumExecutionEnvironment sqee = new SimpleQuantumExecutionEnvironment();
        Result res = sqee.runProgram(p);
        Qubit[] qubits = res.getQubits();

Прежде, чем мы измерим кубиты (и потеряем всю информацию), выведем на экран вероятности. Теперь измеряем кубиты и смотрим значения:

Arrays.asList(qubits).forEach(q -> System.out.println("qubit with probability on 1 = "+q.getProbability()+", measured it gives "+ q.measure()));

Запустив это приложение, получим следующий вывод:

qubit with probability on 1 = 0.50, measured it gives 1
qubit with probability on 1 = 1, measured it gives 1

Обратите внимание: для первого кубита может быть измерено и значение 0, как мы и ожидали.
Если запустить эту программу множество раз, то значение первого кубита в среднем будет равно 0 в половине случаев и 1 в половине случаев.

Это все, что нужно знать о квантовых вычислениях?

Конечно же нет. Здесь мы не затронули ряд важных концепций, в частности, не обсудили запутанность, обеспечивающую взаимодействие между двумя кубитами, даже если физически они находятся очень далеко друг от друга. Не поговорили о самых известных квантовых алгоритмах, среди которых – алгоритм Шора, позволяющий разлагать целые числа на простые множители. Также мы проигнорировали ряд математических и физических фактов, в частности, не учли, что в суперпозиции |x> = a|0> + b|1>, оба числа, a и b, могут быть комплексными.

Однако, основная цель этой статьи заключалась в том, чтобы вы могли составить впечатление о квантовых вычислениях и понять, как они вписываются в будущее разработки ПО.

Let's block ads! (Why?)