ARA: алгоритм для нахождения максимального числа точек на прямой линии

Недавно мне попалась классическая задачка для собеседований: поиск максимального числа точек, стоящих на прямой линии (на плоскости, координаты целочисленные). В голову сразу пришла идея полного перебора, которая имеет очевидную сложность по времени в O(n^2), но мне показалось, что здесь обязано быть что-то ещё, хоть какая-то альтернатива в O(n*log(n)). Через полчаса нашлось даже нечто лучшее!

Сначала я заметил, что можно легко решить задачу только для горизонтальных или вертикальных линий, складывая X/Y каждой точки в словарь. А чем отличаются остальные линии? Всего лишь наклоном?.. А ведь это поправимо!

Таким образом я решил, что можно несколько раз обходить весь список точек вращая их. И получается решение в O(n)! Хотя и с большим коэффициентом. Очень надеюсь, что я изобрёл не велосипед :)

# *** Константы ***

# Число вращений
# Угол одного вращения = 180/ROT_COUNT градусов
#
# Значение должно быть как минимум 12,
# используйте 180*4 для хороших результатов (6% ошибок),
# и 180*20 для лучших (0% ошибок).
# Бóльшие значения повышают время выполнения.
# Меньшие значения приводят к ложно-отрицательным результатам.
ROT_COUNT = 180*10

# Точность
# Алгоритм полезно рассматривать как поиск максимального числа точек,
# лежащих на полоске с шириной равной 1 / MULT_COEF.
# Подходят значения от 4 и выше.
# Большее значение MULT_COEF требует большего ROT_COUNT.
# Бóльшие значения приводят к ложно-положительным результатам.
# Меньшие значения приводят к ложно-отрицательным результатам.
MULT_COEF = 2 ** 3

angles = list(map(lambda x: x*180.0/ROT_COUNT, range(ROT_COUNT)))

def mnp_rotated(points, angle):
        """Returns Maximum Number of Points on the same line with given rotation"""
        # Расчёт преобразований
        rad = math.radians(angle)
        co = math.cos(rad)
        si = math.sin(rad)
        # Количество точек по разным иксам
        counts = {}

        for pair in points:
                # Расчёт нового икса
                nx = pair[0]*co - pair[1]*si

                # Для нормального использования словаря нужно целое число,
                # а умножение на коэффициент предотвращают
                # объединение слишком далёких точек после округления
                # и формирует толщину рассматриваемой полоски
                nx = int(nx * MULT_COEF)

                # Добавляем точку
                if nx in counts:
                        counts[nx] += 1
                else:
                        counts[nx] = 1

        # Выбираем наибольшее число
        return max(counts.values())


def mnp(points):
        """Returns Maximum Number of Points on the same line"""
        res = 0
        best_angle = 0
        # Простой обход всех нужных углов
        for i in angles:
                current = mnp_rotated(points, i)

                # Сохраняем значение, если оно лучше предыдущего
                if current > res:
                        res = current
                        best_angle = i

        return res

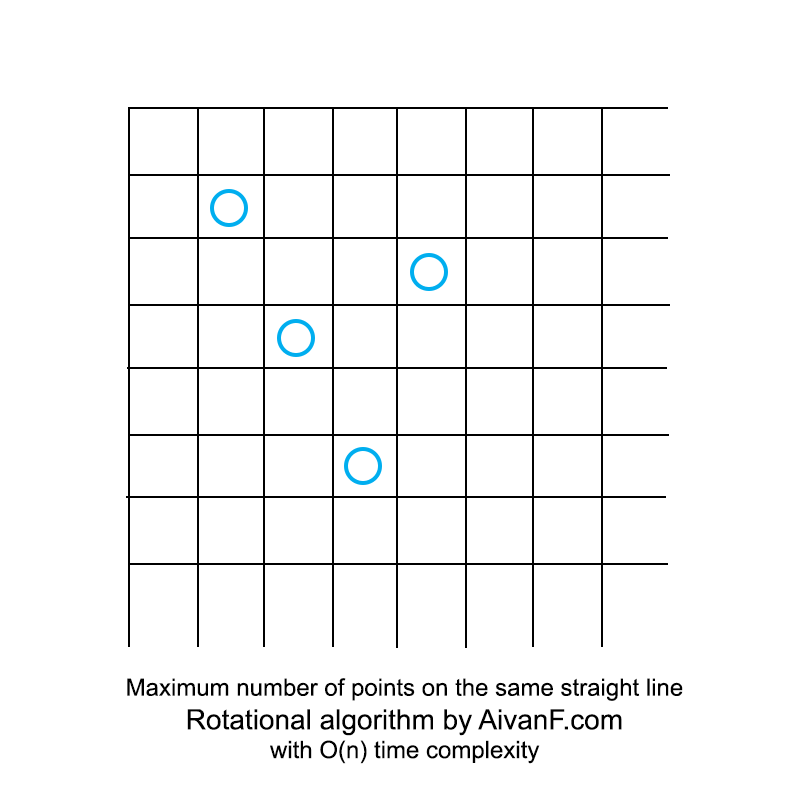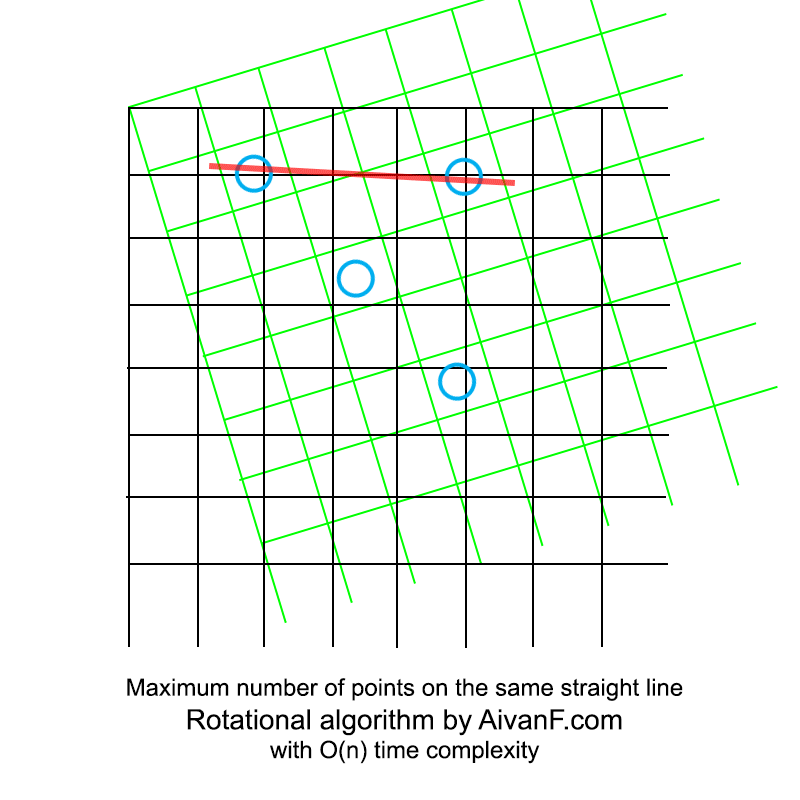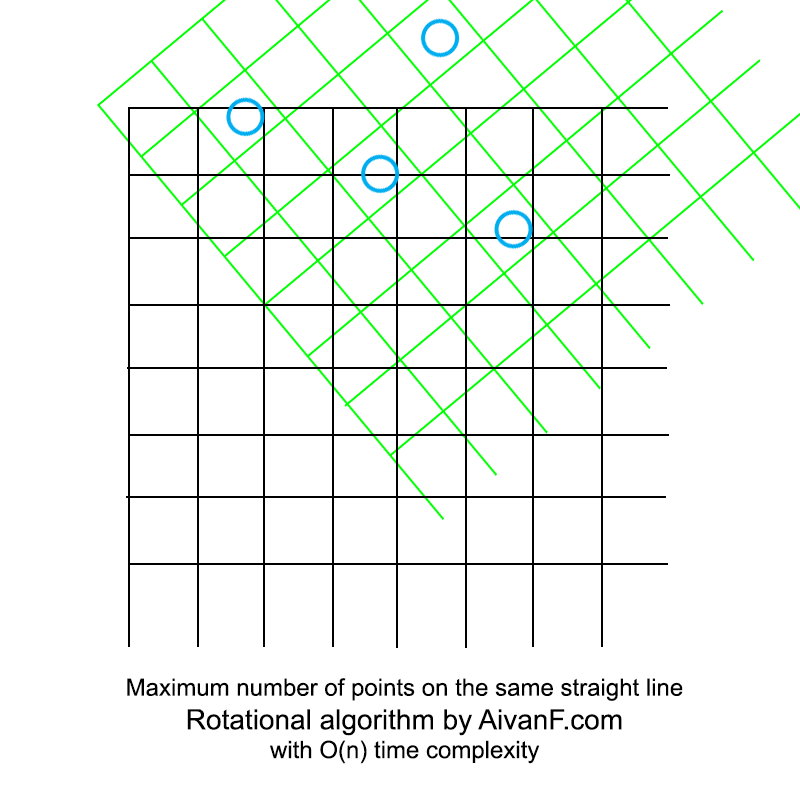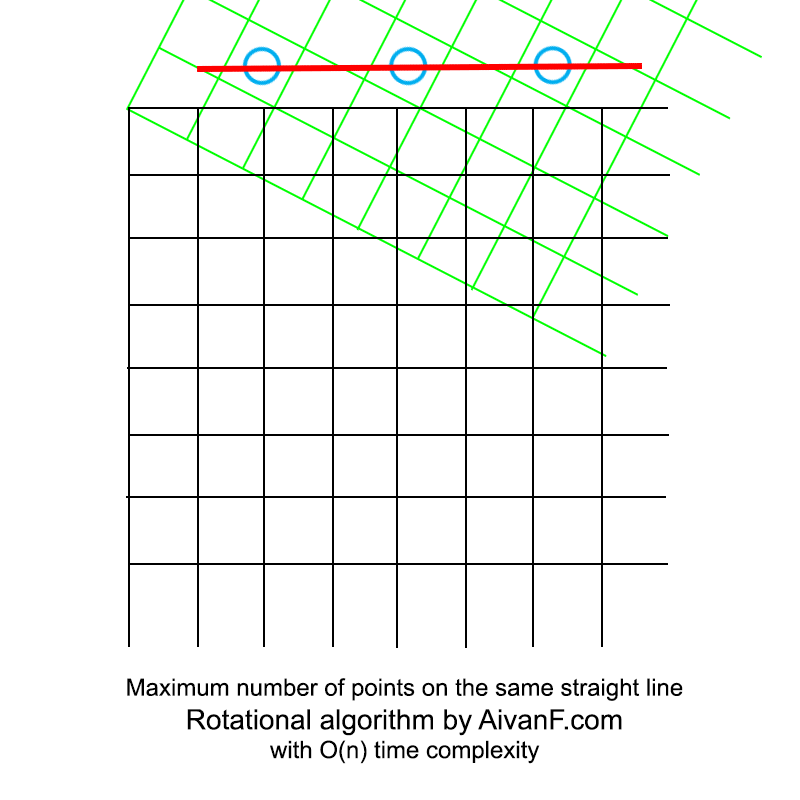
Визуализированно это выглядит примерно так:
_{моя первая самодельная гифка, просьба не ругать:)}

Интересно отметить, что последующая реализация полного перебора заняла больше строк кода.

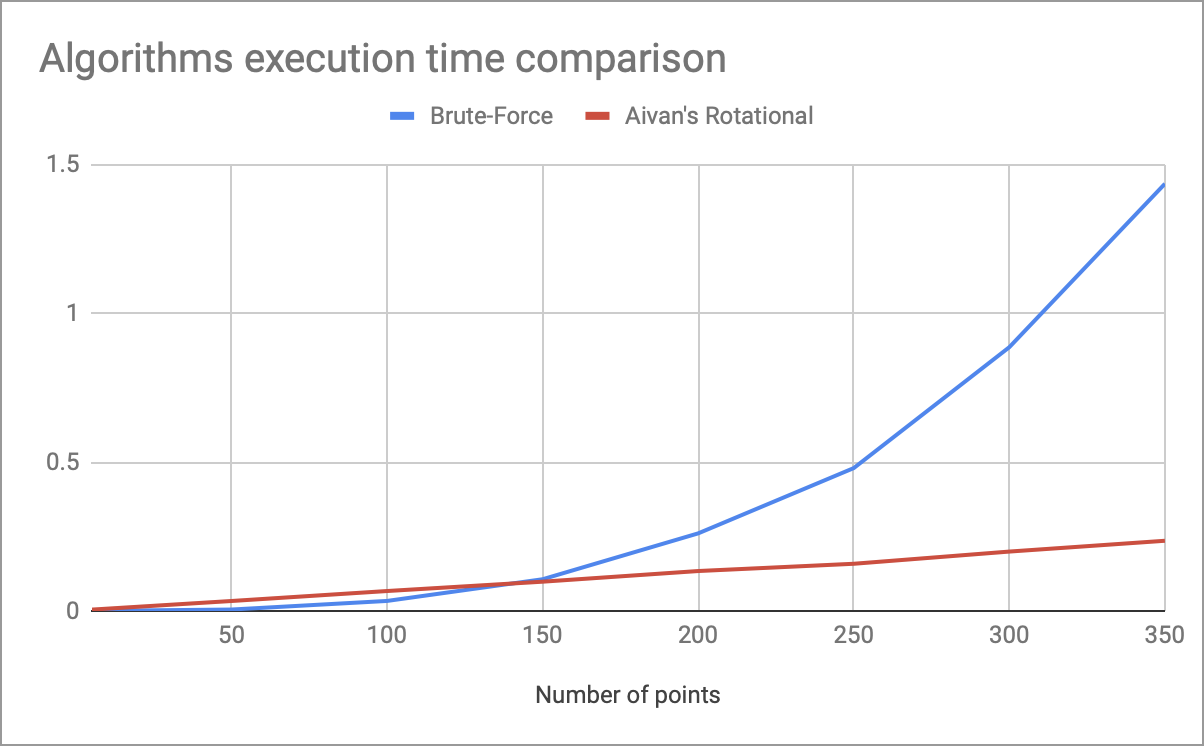
График с замерами времени выполнения моего вращательного алгоритма и полного перебора в зависимости от числа точек есть в шапке.

Открыть график здесь

Примерно на 150 точках проявляется преимущество линейной сложности по времени (при коэффициентах, используемых в коде выше). В итоге, у этого алгоритма есть такие недостатки:

• Точность работы не абсолютная.
• Время выполнения на малых наборах точек велико.
  _{Вообще, это легко исправляется грамотным подбором коэффициентов: для простых наборов вполне достаточно ROT_COUNT = 36, а не 2000, что ускоряет код в 50+ раз.}

И такие достоинства:

• Спокойно работает с дробными координатами.
• Временнáя сложность линейна, что заметно на больших наборах данных.

Таблица с измерения доступна здесь. Весь исходный код проекта с обоими алгоритмами и различными проверками есть на ГитХабе.

Let's block ads! (Why?)