С другой стороны, элементы функционального стиля программирования уже проникли в промышленные языки программирования, такие как Swift и Kotlin. Разработчики этих языков прекрасно знакомы с функциональным программированием, поэтому смогли применить его «в малом», предусмотрев многие, хотя и не все, необходимые компоненты. Чем дальше — тем больше части ФП внедряются в промышленные ЯП, и тем качественнее и полнее реализуется поддержка.
Уметь программировать в функциональном стиле полезно, чтобы упрощать себе работу, и сейчас мы посмотрим, как этим воспользоваться!
Виталий Брагилевский — преподаватель ФП, теории алгоритмов и вычислений, автор книги «Haskell in Depth» и участник комитетов Haskell 2020 и наблюдательного комитета компилятора GHC.
Краткая история
Истории о функциональном программировании не всегда правдивы. Часто о ФП говорят примерно так.
«Давным-давно в далекой-далекой галактике программирование было простым, понятным и хорошим. Алгоритмы и структуры данных запрограммировали и все прекрасно — никаких проблем!
Потом пришли ситхи страшные люди, которые решили, что все программы состоят из классов: «Объектно-ориентированное программирование для всех! Все нужно писать только такими методами.
Когда они набрали силу, разрабатывать ПО стало невозможно — появилась куча проблем. Чтобы спасти несчастных страдающих разработчиков, и существует функциональное программирование».
Главное в спасении — нарисовать красивую и бессмысленную картинку.
Когда вы примените все, что на картинке — наступит счастье, мир, покой, а проблемы разработки ПО будут решены.
История красивая, но на деле все обстоит иначе. Именно так я представляю функциональное и промышленное программирование.

Функциональное программирование это лаборатория Фарадея — место рождения идей, которые потом применяются в промышленном программировании.
В разговоре о промышленных языках программирования понятия, функциональны они или нет, используется там ФП или нет, подниматься не должны!
Главная миссия ФП — передавать хорошие элементы в мейнстримовые языки.
Желать пересадить всех на функциональные рельсы, все равно, что заставить ученых проводить эксперименты как Фарадей — бессмысленно. Никто сейчас не проводит опыты над электричеством такими устаревшими методами.
Рассмотрим на примерах.
Функция Джона Маккарти
Джон Маккарти один из создателей Лиспа.

65 лет назад основным языком программирования был Фортран. В нем есть условный оператор:
IF (I.NE.0) GOTO 40
STMT-1
STMT-2
40 STMT-3
Если значение переменной I не равно 0, то переходим по метке «40».
В то время Джон создавал программу, которая программирует шахматы, и писать в подобном стиле ему было неудобно. Джон подумал, хорошо бы для решения конкретной задачи иметь функцию XIF(M, N1,N2), которая берет условие, и возвращает одно из двух значений: N1 или N2.
Одна из первых идей ФП: от оператора с последовательностями действий «если… то» переходим к функции, и сразу получаем требуемое значение.
Большой недостаток такой функции — одновременное вычисление N1 и N2. Зачем лишние вычисления, если нужно только одно значение?
Маккарти думал и над этой проблемой и пришел к условной тернарной операции:
M==0 ? N1 : N2
В некоторых модных ЯП она считается устаревшей. Но этот элемент функционального программирования есть в любом мейнстримном языке. Мы везде его используем, и иногда вынуждены моделировать другими способами, чтобы все-таки получить условную операцию.
Можно ли освободить программирование от стиля фон Неймана?
Джон Бэкус — создатель Фортрана и очень известный человек. В 1977 году получил премию Тьюринга в области информатики. На вручении награды произнес речь «Можно ли освободить программирование от стиля фон Неймана?». В ней создатель Фортрана — обратите внимание — призвал программировать не так, как мы привыкли.

Один из главных примеров в речи — код, который вычисляет скалярное произведение двух векторов.
Решение задачи можно найти циклом по классической фон-неймановской программе:
c := 0
for i := 1 step 1 until n do
c := c + a[i]*b[i]
Здесь есть сумматор и аккумулятор — циклом перебираем значения и все комбинируем.
Решение этой же задачи можно найти функциональной программой. В качестве примера Джон показал код на выдуманном языке FP.
Def DotP = (Insert +) o (ApplyToAll x) o Transpose
Джон предложил использовать композицию функций —
o, а функции, которые взаимодействуют между собой, писать декларативно.
Два примера — классический и функциональный — выполняют одно и то же действие, но Бэкус считал, что правильнее писать во втором стиле.
Сейчас все так и пишут. Ваши программы скорее всего написаны в таком же стиле.
Как не надо писать
Многие напоминают мне, что когда-то я преподавал Java и студенты писали примерно так же на этом ЯП. Да, но это было давно, мы были молоды и не знали, как писать правильно.

Сейчас, оценивая этот код, я вижу много недостатков:
- используются циклы, которые вложены друг в друга;
- код совершенно нечитаем;
- некорректно проверяются концы строк;
- используются счетчики.
Именно так действительно никто не пишет, что хорошо.
Современный код
Сейчас код выглядит подобным образом:
fun countLinesInFiles(fnames: List<String>): Int
= fnames.map { File(it).readLines().size }
.sum()
Это код на Kotlin, на не самом функциональном ЯП, но писать иначе уже нельзя. Как все работает?
На вход подается список имен файлов, считается количество строк в каждом из них, потом все суммируется и находится общее количество строк. Функциональный элемент — функция «map» — обрабатывает все элементы заданного списка имен файлов. Дальше котлиновское действие, которое мы производим с каждым файлом: считаем количество строк, файл читается и разбивается на строки. Переменная it — это имя конкретного файла на каждом шаге такого цикла. В конце считается сумма элементов — sum().
Если мы знаем, что такое map и фигурные скобки в Kotlin, нам понятно, что выполняет код. Мы не гадаем, каким именно символом заканчивается строка в этой конкретной операционной системе. Это не важно — readLines все делает за нас.
Почти как в Haskell
Но если приглядеться, то мы увидим Haskell.
countLines :: FilePath -> IO Int
countLines = fmap (length . lines) . readFile
countLinesInFiles :: [FilePath] -> IO Int
countLinesInFiles = fmap sum . traverse countLines
Разница, конечно, есть. В Haskell я напишу две функции, а не одну, потому что это функциональное программирование.
Первая функция считает число строк в одном заданном файле. Мы сразу видим, что происходит: на входе имя файла, на выходе Int — целое число.
Контроль побочных эффектов. Мы используем «IO», потому что в Haskell нужно сигнализировать, что функция использует побочные эффекты и выполняется ввод-вывод. Это «нечистая функция», поэтому здесь не просто Int, а IO Int. Это сигнализирует, что число получено в результате исполнения побочных эффектов.
Вторая функция считает количество строк уже в нескольких файлах. Квадратные скобки — это список в Haskell. Мы берем список имен файлов — FilePath, и получаем тот же самый IO Int — суммирование. Следующая строка: сумма, traverse — обход по списку, а для каждого элемента списка выполняется действие «countLines».
Композиция функций. Везде используется операция «. » (у Бэкуса o) — это композиция функций. Мы пишем функции слева направо, но выполняются они справа налево.
«f. g» — это функция, которая по аргументу «x» возвращает значение «f(g(x))». Аргументов нигде нет, они будут подставлены сами. Я использую такую аннотацию, потому что для ФП она очень удобна. В этом мейнстримные языки пока отстают.
Разница между ООП и ФП
Мы программируем практически в функциональном стиле на современных нефункциональных языках.
Если копнуть глубже, то видно, что особой разницы между ООП и ФП нет. ООП — практически то же, что и ФП.
Докажу утверждение на простом примере реализации UML-диаграммы. Классический пример: форма, круги, квадраты, наследование, виртуальные функции.
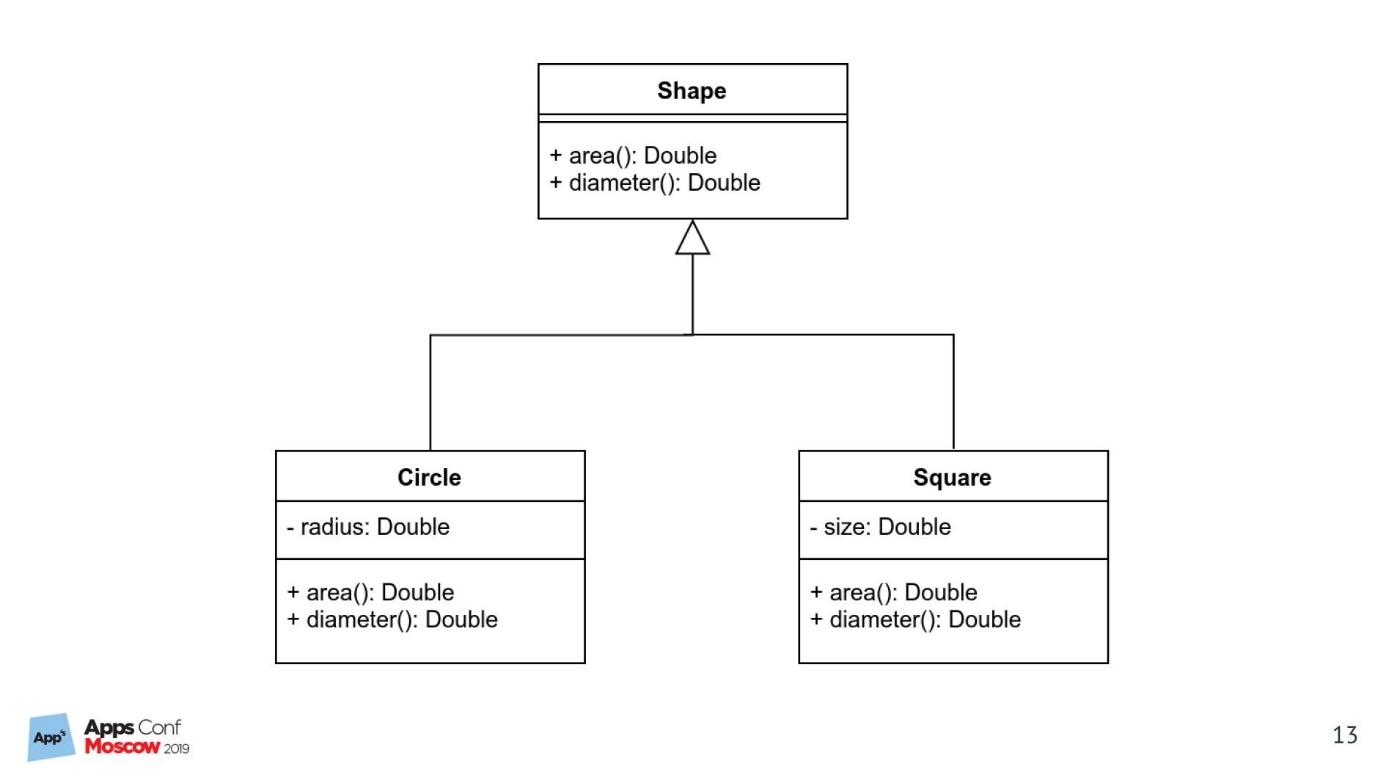
Реализация на Swift
Я недавно узнал, что это уже не ООП, а протокол-ориентированное программирование. Но в Swift я ничего не понимаю, поэтому получилось, что получилось.
protocol Shape {
func area() -> Double
func diameter() -> Double
}
class Circle: Shape {
var r = 0.0
init(radius: Double) {
r = radius
}
func area() -> Double {
return 3.14 * r * r
}
func diameter() -> Double {
return 2 * r
}
}
class Square: Shape {
var s = 0.0
init(size: Double) {
s = size
}
func area() -> Double {
return s * s
}
func diameter() -> Double {
return sqrt(2) * s
}
}
Вроде бы работает, но не ООП.
В реализации все просто: сериализация, методы, конструктор – все, как положено. Это классическое ООП в стиле Гради Буча.
Запустим этот код, например, на круге и на квадрате.
func testShape(shape: Shape) {
print(shape.area())
print(shape.diameter())
}
Получим результат. Все работает.
testShape(shape: Circle(radius: 5))
testShape(shape: Square(size: 5))
78.5
10.0
25.0
7.0710678118654755
Здесь должен работать полиморфизм, но поскольку это ПОП, а не ООП, наверное, работает что-то другое. Но это не важно – главное, что работает.
Реализация на Haskell
Вот код на Haskell, который выполняет то же, что и код на Swift.
data Shape = Circle Double | Square Double
area :: Shape -> Double
area (Circle r) = 3.14 * r * r
area (Square s) = s * s
diameter :: Shape -> Double
diameter (Circle r) = 2* r
diameter (Square s) = sqrt 2 * s
В ФП данные и функции существуют отдельно. В первой строке у нас тип данных, который мы называем «алгебраическим типом данных» — это круг или квадрат. Дальше операция «или» используется для построения типа данных. И пара функций считают площадь и диаметр.
Функции используют сопоставление с образцом — проверяют, круг это или квадрат, и выбирают соответствующую строчку. Так это работает в Haskell — отдельно. Функции вызываются для одного, для другого и считаются результаты.
Результат:
> area (Circle 5)
78.5
> diameter (Circle 5)
10.0
> area (Square 5)
25.0
diameter (Square 5)
7.0710678118654755
Понятие диаметра — расстояния между двумя самыми удаленными точками фигуры — используется для фигуры любой формы, в квадрате это диагональ.
Кажется, что в Swift и Haskell подходы противоположны. У нас есть класс и его наследники, которые мы реализуем, и два вида сущностей, для каждой из которых пишем функции. Однако, если представить наш код в виде таблицы, где столбцы — типы форм, а строки — функции, то видно, что разницы нет.
ООП — это работа с этой таблицей по столбцам, где каждый столбец — один класс. ФП — это работа с таблицей по строкам, потому что речь идет о функциях.
Какая разница, как работать с таблицей и как на нее смотреть: через строки или столбцы? Для соответствующих концепций это не имеет значение. Это важно только для нас как наблюдателей.
Разница есть техническая, когда мы проводим диспетчеризацию:
- в ООП — до вызова функции по указателю на таблице виртуальных методов;
- в ФП — после вызова функции, когда мы смотрим, какая сущность пришла в функцию, и выбираем нужную строчку.
Идеологически — это просто работа с таблицей.
Алгебраические типы данных
Известно, что алгебраические типы данных есть и в Swift.
Код в Haskell…
data Shape = Circle Double | Square Double
… в Swift будет немного многословнее.
enum Shape {
case Circle(radius: Double)
case Square(size: Double)
}
Но идея та же. Не считая операции «или» для алгебраических типов данных, вместо которой в Swift используется «enum», реализация аналогична. Например, функцию можно оформить в виде метода расширения.
Код в Haskell…
area :: Shape -> Double
area (Circle r) = 3.14 * r * r
area (Square s) = s * s
… в Swift многословнее.
extension Shape {
var area: Double {
switch self {
case .Circle(let r): return 3.14 * r * r
case .Square(let s): return s * s
}
}
}
Но, опять же — идея та же.
Алгебраические типы данных присутствуют и в Kotlin:
sealed class Shape {
data class Circle(val radius: Double): Shape()
data class Square(val size: Double): Shape()
}
fun area(sh: Shape): Double {
return when (sh) {
is Shape.Circle -> 3.14 * sh.radius * sh.radius
is Shape.Square -> sh.size * sh.size
}
}
Слов больше, но идеологически — аналогично.
После этого мы будем говорить, что Kotlin и Swift не функциональные ЯП? Они же используют эти элементы, потому что, неожиданно, это удобно. Элементы из ФП пришли в мейнстримные языки, и уже мейнстримные языки можно не называть объектно-ориентированными, потому что все самое хорошее из ФП они уже давно используют.
Проблема расширения
Есть еще одна разница между ООП и ФП. Существует ограничение в том, что если мы хотим расширить таблицу, добавить еще один столбец или строку, то выясняется, что некоторые способы расширить табличку в одной парадигме работают хорошо, а в другой плохо.
В ООП можно легко написать один класс, но чтобы добавить еще один метод, придется лезть в базовый класс, что-то добавлять — все перекомпилировать. Возникает масса сложностей. В ФП также: при добавлении нового объекта возникнет проблема — мы должны перекомпилировать определение базового типа. А функцию добавить, наоборот, легко.
В правом нижнем углу находится самое тяжелое для обоих способов. Невозможно это сделать красиво.
Исследователи уже двадцать лет бьются над проблемой расширения. Этой задачей часто тестируют выразительность ЯП. Основной пример — это что-то вроде задачи компиляции игрушечного языка программирования, когда мы хотим добавлять в него языковые конструкции — добавлять типы и расширять операции, статически контролировать типы. Но при этом мы не хотим ничего перекомпилировать и явно приводить типы — все должно выполняться компилятором автоматически.
Подходы к решению
У проблемы расширения — базовой дилеммы между ООП и ФП — решений много. Последние 20 лет они публикуются, и многие ЯП уже их внедряют.
- Паттерн «Visitor». Решение, которое возникло еще до того, как была сформулирована сама проблема. Метод хорошо работает, но с ограничениями.
- Мультиметоды.
- Открытые классы — методы расширения.
- Классы типов.
- Алгебры объектов.
Все перечисленные подходы, и даже решение с ужасным названием «Алгебры объектов», так или иначе решают проблему расширения. Подробно не будем останавливаться. Но если вам интересны именно языки программирования, а не само программирование — изучите самостоятельно, вам будет интересно.
Об алгебрах
Хочу поговорить не совсем об алгебрах, а вообще об этом слове.
Когда я встречаю функциональщика, то сразу слышу страшные слова: полугруппы, моноиды, функторы, монады. Иногда кажется, что функциональщики доказывают справедливость этой старой картинки.

Ее однозначно нарисовали адепты Haskell. Кто другой будет представлять себя в виде Эйнштейна, думать, что все представляют его Эйнштейном, и разговаривать «страшными» словами?
Каждое страшное слово, вроде «функтора» — это просто конкретная проблема в программировании и ничего больше.
Полугруппы и моноиды упрощают компоновку сущностей в сущности того же рода — паттерн «Composite». Есть моноиды и полугруппы. Мы просто берем сущности, компонуем их и получаем сущности того же рода для удобства обработки.
Например, операция конкатенации строк в Kotlin — это обычное использование моноида.
val a = "Hello "
val b = "world"
val c = a + b
Когда я читаю лекции по общей алгебре, говорю: «Программисты, строки складывать умеете? Вот это и есть моноид». Можно дать формальное математическое определение, но кратко и без формализма — это компоновка двух строк во что-то одно.
Второй пример — компоновка свойств HTTP-запроса. В воображаемом Kotlin это выглядит так:
val a = HttpReq("f","v1")
val b = HttpReq("f2","v2")
val c = a + b
В реальном Haskell есть библиотека, которая выполняет ровно то же. Там свойства HTTP-объекта — это моноид. Мы складываем их и формируем из отдельных компонентов новый HTTP-запрос.
То же с монадами и функторами. Функторы и монады облегчают описание последовательности шагов вычисления в контексте. Шаги идут последовательно друг за другом и каким-то образом зависят друг от друга. Зависимость — не просто последовательное выполнение, но еще и некий контекст — то, что существует кроме этих шагов. Программисты на современных ЯП иногда используют «optional chaining», например, в Swift.
if let johnsStreet = john.residence?.address?.street
{ /* SUCCESS */ } else { /* FAILURE */ }
Мы пытаемся вычислить адрес, достать его из объекта. Есть объект «john» — извлекаем местожительство.
?.значит, что местожительство может отсутствовать, в этом случае сразу получим false.- Но если местожительство присутствует, то достаем из него адрес.
- Адрес тоже может отсутствовать.
- Если присутствует — достаем строку.
Вычисление идет последовательно: достаем из объекта сначала одно, потом другое, потом третье. Контекст здесь — возможность отсутствия соответствующего значения. Если оно отсутствует, то возвращаем ветку else — неуспешный результат в данном случае. Мы можем прерваться на любом шаге.
Создатели Swift не стали пугать программистов монадой. Они знают, что такое монада, и ввели в язык синтаксис, который выполняет монадические вычисления: последовательность шагов в контексте с отсутствием значения.
Если бы мы писали тот же самый код с монадой на Haskell, он бы выглядел так.
case residence john >>= address >>= street of
Just johnsStreet -> -- SUCCESS
Nothing -> -- FAILURE
Обратите внимание, «>>=» — это главная операция монадического связывания. Но смысл кода от этого не меняется.
В Swift для «optional chaining» понадобилось вводить новую синтаксическую конструкцию. В Kotlin для корутин тоже нужно вводить кучу синтаксиса и понятий. В Haskell те же самые корутины неожиданно превращаются в те же самые монадические вычисления, с тем же самым оператором «>>=».
Есть два подхода к монаде:
- Расширять языки программирования, прятать абстракцию монадического вычисления от программиста, давая ему при этом возможность этим пользоваться.
- Выпячивать абстракцию, как в Haskell.
Оба подхода хороши. Но идея выноса абстракции наверх в больших мейнстримных ЯП пока не считается хорошей. Считается, что лучше вводить много разных элементов синтаксиса и прятать от программиста единое понимание сути происходящего. Может быть, это и хорошо — так проще, чем подниматься на более высокий уровень абстракции.
Если у вас множество сущностей, и вы к ним применяете разные операции — это алгебра.
Массу «алгебр» в своих мобильных разработках вы уже используете. Все программирование — это сущности, которые мы обрабатываем разными способами. Мы обычно не называем это «алгебрами», но это они и есть. Поэтому теперь понятие «алгебра объектов» не будет нас пугать.
Абстракция — это хорошо или плохо?
Нет однозначного ответа на этот вопрос. Разработчики языков программирования самостоятельно принимают решение, что они делают — выносят абстракцию программистам или прячут ее за элементы синтаксиса.
Я считаю, что абстракция — это красиво. Покажу это на примере со сложным синтаксисом Haskell из работы «Build Systems a la Carte» Андрея Мохова из университета Ньюкасла и его соавторов. Соответствующая статья получила премию Distinguished Paper Award на International Conference on Functional Programming (ICFP) в Сент-Луисе осенью 2018 года. Эта замечательная работа посвящена Build-системам, которые все используют.
Авторы предлагают абстрагироваться от конкретных Build-систем и выражать разные Build-системы с помощью одной формализации — абстракции. Для этого они вводят понятие хранилища.
data Store i k v
В нем есть параметры:
- i — постоянная информация системы сборки;
- k — ключи зависимости, например, имена файлов в сборке;
- v — сами значения, то есть результаты сборки, например, собранные файлы.
Хранилище — это абстракция. Один из примеров — файловая система с файлами, с дополнительной метаинформацией. У файлов есть имена и содержимое на диске.
Также есть зависимости. Мы хотим показать, что одни файлы зависят от других файлов, чтобы их собирать. Чтобы собрать объектный файл, нужно сначала найти на диске то-то и то-то, собрать, а потом это все вместе использовать.
Есть другая абстракция — «Task» — задание для системы сборки.
newtype Task c k v = Task { run :: forall f. c f => (k -> f v) -> f v }
Здесь используется сложный синтаксис Haskell, потому что абстрагируется все. Например, монада — это частный случай «f», от которого происходит абстрагирование. Кроме монады, могут быть и другие способы описывать последовательности вычислений.
Что происходит? Функция «k -> fv» описывает зависимость между ключом и значением — это способ построить что-то одно. Эта функция играет роль параметра. В результате применения этой функции мы получаем итоговое значение. Так описывается сборка одного компонента Build-системы.
Выстраивание дерева выполняется уже следующим типом — набором заданий:
type Tasks c k v = k -> Maybe (Task c k v)
Это тоже функция, которая описывает, как от разных ключей зависят разные способы сборки. «Maybe» — это что-то вроде «optional». Мы описываем, как что-то от чего-то зависит, или не зависит.
В результате получаем окончательную абстракцию Build-системы:
type Build c i k v = Tasks c k v -> k -> Store i k v
-> Store i k v
На входе описание всей системы зависимостей. Затем идет ключ k, с которого начинается сборка. Дальше — начальное хранилище и хранилище с результатом функции с полностью собранной системой. Это пример абстракции, которая построена поверх других абстракций.
Андрей Мохов с соавторами выявили отличия и привели в статье формальное описание для четырех систем сборки.
- Make,
- Shake — аналог Make для Haskell,
- Bazel,
- Excel.
Первые три системы сборки известны многим. Четвертая — Excel — это тоже система сборки. Excel тоже попадает под абстрактную формализацию — в нем клетки зависят друг от друга. Написали значение в одну клетку, пересчиталось что-то другое. Make и Excel имеют что-то общее, что можно описывать с помощью этой абстракции.
ФП — это очень медленно
Это частая претензия к функциональному программированию.
— Ваш Haskell тормозит. Мы уже все давно посчитали, а вы все еще пишете свою программу и никак скомпилировать не можете.
Иногда да, иногда нет. Вообще-то быстродействие — это задача компилятора. В идеальной системе хороший компилятор должен построить хороший код, независимо от того, что написал программист. Если он строит плохой код, то это вина компилятора.
Декларативность не должна мешать производительности
Например, высокодекларативный код на Haskell:
h :: [a] -> Int
h = length . filter p . map g . map f
Можете считать это псевдокодом — я использую композицию функций. Я принимаю на вход какой-то список, а дальше:
map f— применяю к каждому элементу функциюf;map g— к каждому элементу применяю функциюg;filter p— фильтрую все: применяю предикат, выкидываю все, что не удовлетворяет предикату;length— считаю длину получившегося списка — сколько элементов в результате удовлетворяет всем этим условиям.
Любой программист мейнстрим языка сразу начнет кричать:
— Ужас, сколько тут циклов, сколько промежуточных структур данных… Это вообще не программирование! Вон из профессии!
Просто потому, что компилятор слабоват.
Fusion
В функциональных ЯП существует идея «fusion», которая потихоньку проникает в другие языки программирования.
Что такое «fusion»? По-простому: всю декларативную тщательно расписанную последовательность шагов можно превратить в императивный цикл:
c := 0
foreach (x : xs)
if p(g(f(x)))
then c := c + 1
Обращаю внимание, что цикл один (!), а промежуточных структур данных ноль (!). Задача компилятора в том, чтобы красивый и понятный код превратить в высокоэффективную программу, и скомпилировать это все в 2-3 ассемблерные команды.
Мы, как программисты, думаем, что это мы пишем медленные программы. Но это не наша вина — это компилятор виноват.
Пусть разработчики компиляторов получше думают и пишут свои компиляторы так, чтобы код получался эффективным.
Вычисления на GPU? Без проблем!
Еще один пример кода на Haskell, который считает скалярное произведение двух векторов:
dotp :: Acc (Vector Float) -> Acc (Vector Float) -> Acc (Scalar Float)
dotp xs ys = fold (+) 0 (zipWith (*) xs ys)
Неважно, что происходит на Haskell: берем 2 вектора, покомпонентно перемножаем, находим сумму компонентов. Важно, что на Haskell этот код после компиляции работает непосредственно на GPU. Векторы размещены сразу на GPU, и графический ускоритель все сделает: скомпилирует CUDA, Open CL — все, что хотите. Библиотека Accelerate у Haskell скомпилирует — получится эффективный код.
На CUDA мы бы писали 100 лет, а здесь написали одну короткую строчку в функциональном стиле, и получили высокоэффективную программу. Все декларативно и быстро! Это ровно то, чего мы хотим от компилятора. Но есть проблемы, с которыми пока компиляторы не очень хорошо справляются.
Каррирование
Каррирование — это большая проблема. Что это такое? Есть функция с тремя параметрами типов a, b, c и результатом D.
f :: A -> B -> C -> D
f a b c = ...
Одно дело, когда мы работаем просто с этой функцией — передаем ее в качестве параметра. Другое дело, когда мы указали аргументы частично:
f :: A -> B -> C -> Df a :: B -> C -> Df a b :: C -> Df a b c :: D
Во второй и третьей строчках мы часть аргументов указали, а часть нет. Если такую функцию, которая частично применена, будем куда-то передавать, то возникнут проблемы. Компиляторы пока не очень хорошо умеют это делать — создается замыкание, много всего требуется передавать, тратить массу времени.
Поэтому во многих языках, например, в Scala действуют по-другому.
f :: A -> (B , C) -> D
f a p = …
f :: A -> B -> C -> D
f a :: (B, C) -> D
f a p :: D
Они говорят: «Это ты можешь откаррировать, а это нет. Эти два аргумента разделить нельзя, они должны всегда идти вместе. Тут скомпилируем, а здесь — нет». В результате ЯП ограничивает возможности программиста.
Это открытая проблема, которая пока еще не решена даже в функциональных языках.
В ФП проще гарантировать корректность
Корректность хорошо работает в ФП. В Haskell 15 лет назад родилась библиотека QuickCheck, которая помогает в тестировании корректности.
Например, есть функция, которая оборачивает строку:
reverse :: String -> String
reverse = ...
Мы ее тестируем, придумывая свойство этой функции. Если два раза применим ее к одной и той же строке, то получится исходная строка.
> quickCheck (\s -> reverse (reverse s) == s)
+++ OK, passed 100 tests.
Да, это чистая функция и для нее можно придумать такое свойство. Библиотека генерирует случайным образом массу аргументов, в данном случае 100, на них прогоняет, и убеждается, что это свойство выполняется.
Мы проверяем работоспособность кода не на конкретных примерах, а формулируем свойство и говорим, что для всех аргументов это свойство должно выполняться. Работаем математически. Эта идея возникла в Haskell 15 лет назад. Сейчас подобные идеи проникают в другие языки. Уверен, что для Swift и Kotlin подобные библиотеки уже есть.
Пример с ошибкой
Как думаете, здесь произойдет ошибка?
abs :: Int -> Int
abs x = if x < 0 then 0 - x else x
head :: [a] -> a -- Функция не определена на пустом списке!
head (x:_) = x
example :: Int -> Int
example x = if abs x < 0 then head [] else x
Обратите внимание, функция в середине работает на непустом списке.
head :: [a] -> a -- Функция не определена на пустом списке!
head (x:_) = x
Если подали непустой список, функция
head возвращает ее голову, а на пустом списке она просто не работает — должна вылететь.
Попадем ли мы на «head», вызванный для пустого списка? Нет, и LiquidHaskell может это доказать. LiquidHaskell — это статический верификатор Haskell-кода.
{-@ abs :: Int -> { n : Int | 0 <= n } @-}
abs :: Int -> Int
abs x = if x < 0 then 0 - x else x
{-@ head :: { xs : [a] | 1 <= len xs } -> a @-}
head :: [a] -> a -- Функция не определена на пустом списке!
head (x:_) = x
{-@ head :: { xs : [a] | 1 <= len xs } -> a @-}
head :: [a] -> a -- Функция не определена на пустом списке!
head (x:_) = x
Можно сказать, что у функции abs результатом будет всегда число, больше или равное n.
{-@ abs :: Int -> { n : Int | 0 <= n } @-}
abs :: Int -> Int
abs x = if x < 0 then 0 - x else x
Здесь пишем, что функция определена на списке с некоторой длиной.
{-@ head :: { xs : [a] | 1 <= len xs } -> a @-}
head :: [a] -> a -- Функция не определена на пустом списке!
head (x:_) = x
Здесь доказываем, что функция возвращает то, что ей передали. Функции передается x и возвращается также x.
{-@ example :: x : Int -> { y : Int | x == y } @-}
example :: Int -> Int
example x = if abs x < 0 then head [] else x
Компилятор или его компонент может проверить вашу программу и доказать целый ряд свойств вашей программы, и она оказывается безопасной. Это пока еще функциональное программирование, потому что активно используется работа с чистыми функциями. Вполне возможно, что подобное когда-нибудь увидим и в мейнстримных языках. Какие-то попытки для объектно-ориентированных языков уже были, например, в Eiffel, значит что-то близкое можно сделать.
А это ещё что?
Это пример веб-разработки:
type MyAPI = Get '[PlainText] String
:<|> "conf" :> Get '[JSON] String
:<|> "year" :> Get '[JSON] Int
:<|> "like" :> Get '[JSON] Bool
myAPI :: Server MyAPI
= root :<|> year :<|> conf :<|> like
В Haskell есть библиотека Servant, которая может моделировать вызовы API с помощью типов. Например, в коде выше есть несколько url для конференции, для года, нравится она или нет, а результаты кодируются в JSON. Видно, что есть разные типы результатов: String», Int», Bool.
Мы пишем разные обработчики.
root :: Handler String
root = pure "Welcome to my REST API"
conf :: Handler String
conf = pure "AppsConf"
year :: Handler Int
year = pure 2019 conf
like :: Handler Bool
like = pure True
А библиотека контролирует всё — результаты такие, какими они должны быть.
Все работает, система типов охраняет корректность нашей программы. Мы не сможем при всем желании вернуть строку вместо целого числа в ответ на запрос о годе, просто потому, что компилятор не пропустит. Корректность — это очень хорошо.
Выводы
Функциональное программирование — интересная штука. Не призываю всех переходить на него, но его элементы мигрируют во все обычные ЯП. И это прекрасно.
Если интересно — начните с книги Уилла Курта «Программируй на Haskell». На русском она вышла в ноябре 2018 года. Трое моих студентов ее перевели, а я подредактировал. Рекомендую книгу всем новичкам в Haskell. Когда освоите все 600 страниц, переходите к следующей.
«Haskell in Depth» за авторством некоего Виталия Брагилевского. Книга пока в раннем доступе, не закончена, но уже рекомендую. Промокод «slbragilevsky» дает скидку 42%.
На Saint AppsConf мы рассчитываем, что в рамках нового Introductory-трека Виталий поможет нам определить раз и навсегда, с какого языка лучше начать изучать программирование. Но основной фокус конференции, конечно, будет на технологиях мобильной разработки. Подавайте заявки до конца августа, если у вас есть интересный опыт в iOS, Android, кросс-платформе или архитектуре — эта памятка поможет конкретизировать тему. Если знаете, о чем мобильным разработчикам стоит задуматься вне контекста программирования, тоже ждем тезисы.За новостями программы следите в рассылке и telegram-канале, видео прошлых докладов смотрите здесь.
Комментариев нет:
Отправить комментарий