
В этой статье мы дадим определение, перечислим правила размещения элементов в красно-чёрном дереве, рассмотрим алгоритм балансировки и закрепим сказанное на примере. Более подробно эту тему, а также другие виды двоичных деревьев поиска мы изучаем на курсе «Алгоритмы для разработчиков».
Красно-чёрное дерево — самобалансирующиеся двоичное дерево поиска, которое гарантирует логарифмический рост высоты дерева от числа узлов и быстрое выполнение основных операций дерева поиска: добавление, удаление и поиск узла.
Красно-чёрное дерево не является полностью сбалансированным, в некоторых местах его высота может различаться почти в два раза. Такое допущение ассимптотически не влияет на скорость поиска элементов, но значительно ускоряет размещение новых элементов, потому что не нужно каждый раз при добавлении элементов «сильно трясти» дерево, иной раз достаточно просто добавить красный элемент, не трогая остальные и не изменяя «чёрную высоту».
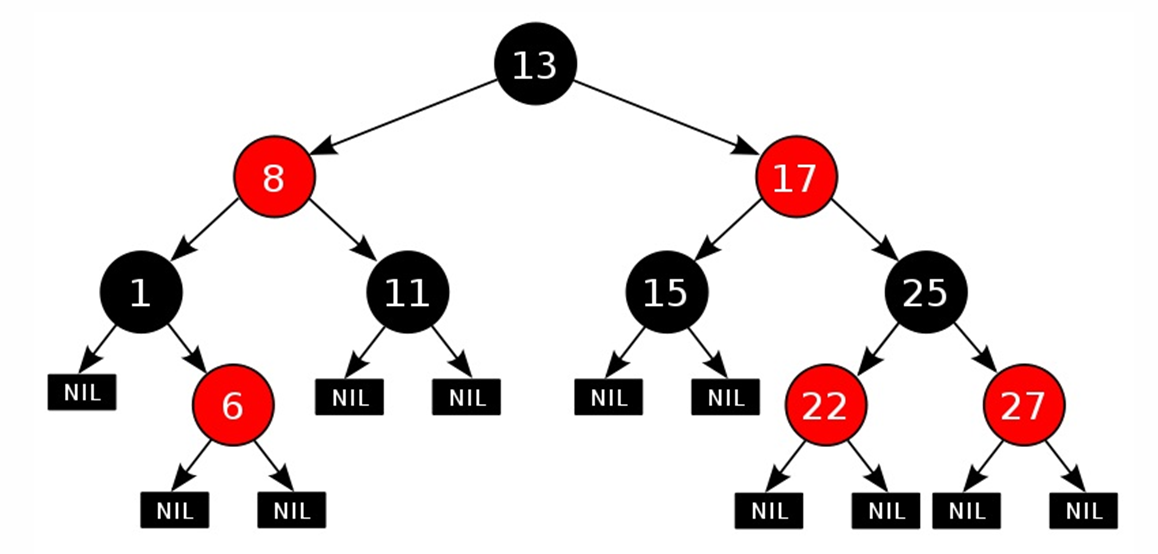
Правила размещения элементов в красно-чёрном дереве
- Каждый узел либо красный, либо чёрный, NIL-листья всегда чёрные.
- Корень дерева всегда чёрный
- Оба потомка каждого красного узла — чёрные
- Путь вниз от любого узла до любого листа-потомка содержит одинаковое число чёрных узлов.
При вставке нового элемента ему присваивается красный цвет. Для выполнения первых двух правил достаточно просто перекрашивать новые вершины в нужный цвет.
Рассмотрим правила балансировки для выполнения 3 и 4 пункта.
На каждом рисунке предполагается, что мы уже добавили элемент Х, который нарушает 3 правило, нужно так изменить структуру дерева, чтобы 3 правило выполнялось, а 4 не нарушилось.
Условные обозначения вершин:
- X — добавленный элемент, который нарушает 3 пункт правил.
- P — папа элемента Х
- G — дедушка элемента Х, папа элемента Р
- U — дядя элемента Х, брат элемента Р, второй сын элемента G.
Случай первый — красный дядя.
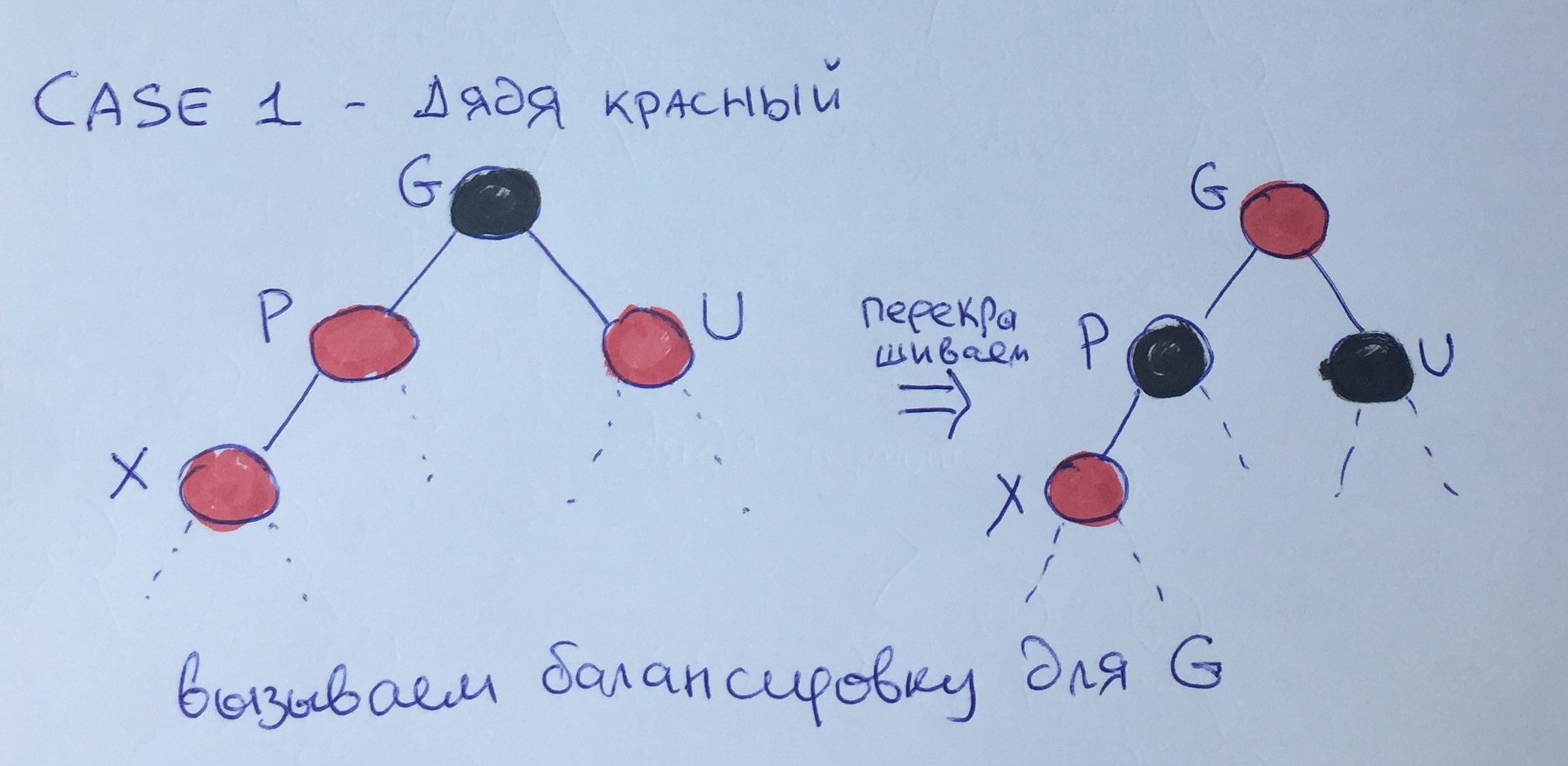
Если и отец, и дядя красного цвета, то мы можем «спустить» чёрный цвет с уровня деда на уровень отца и перекрасить узлы, как показано на рисунке. В этом случае «чёрная высота» останется прежней, однако возможно нарушение 3 правила для элемента G, поэтому необходимо рекурсивно вызвать дальнейшую балансировку для этого узла.
Случай второй — чёрный дядя — папа и дед в разных сторонах.
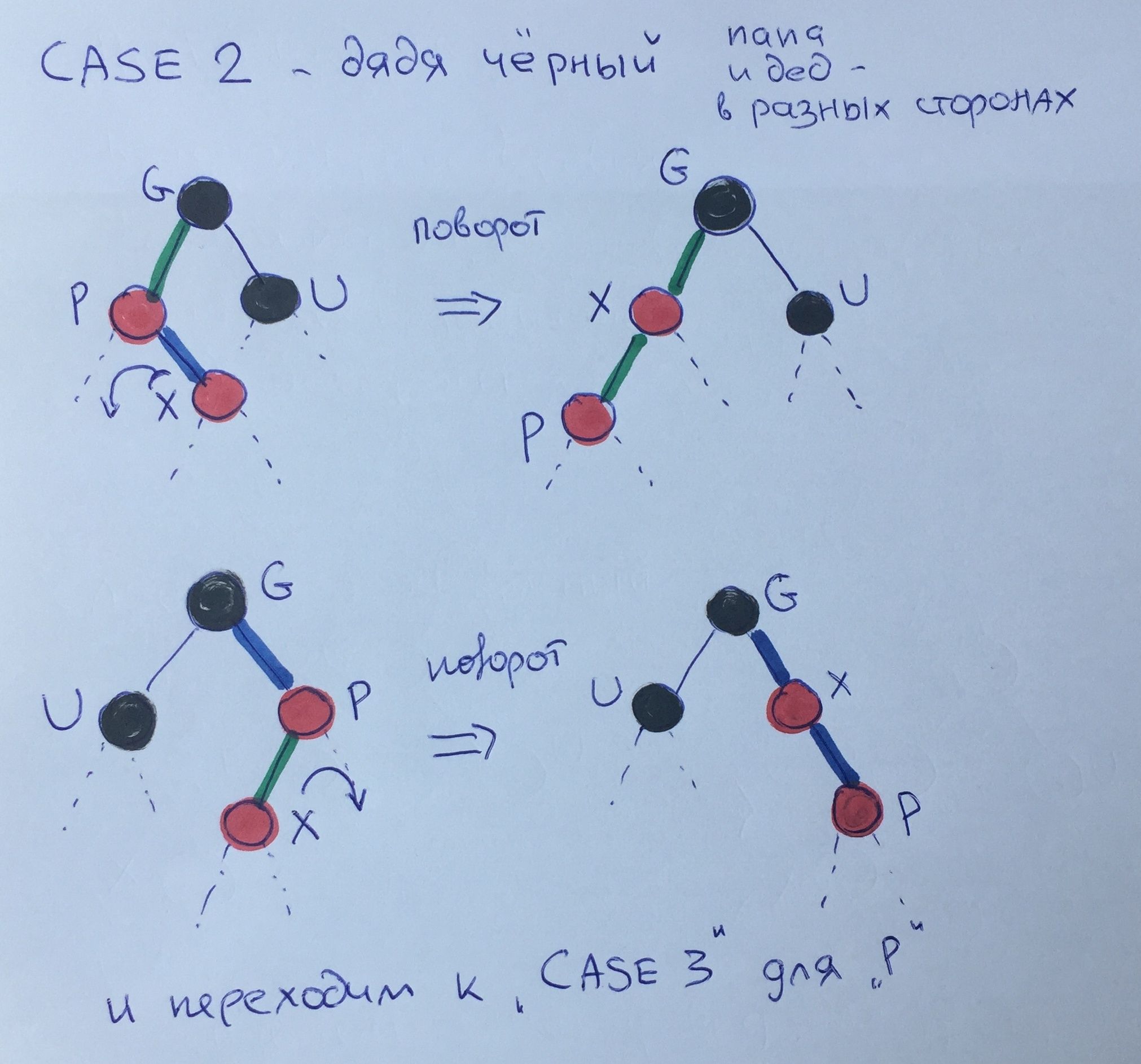
Эту структуру необходимо привести к третьему случаю, когда папа и дед идут в одну сторону. Для этого нужно выполнить малый поворот от сына Х к его отцу (правила поворотов в этой статье не рассматриваются) и вызвать 3 случай для элемента Р.
Случай третий — чёрный дядя — папа и дед в одной стороне.
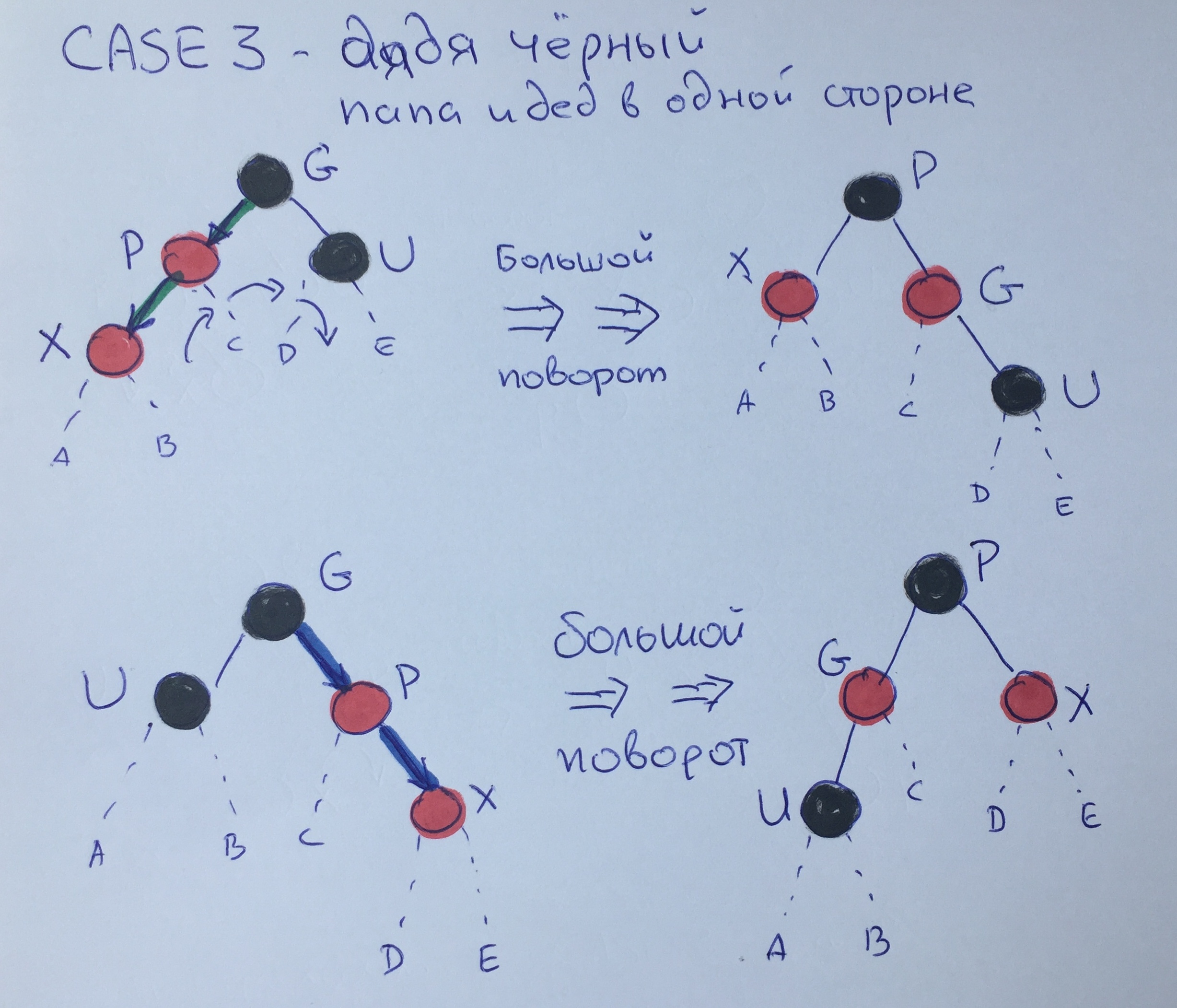
В этом случае мы уже можем совершить большой поворот от отца через деда к чёрному дяде и перекрасить Р в чёрный, а G в красный. В результате этого поворота 3-правило будет выполнено.
Убедимся, что 4 правило тоже выполняется. Предположим, что до большого поворота чёрная высота элемента G была N+2. Тогда высота «подвешенных» элементов будет следующей:
A = N+1,
B = N+1,
C = N+1,
D = N,
E = N.
Убедитесь сами, что после поворота 4-правило выполняется для всех элементов.
Конкретный пример
Теперь рассмотрим процесс формирования красно-чёрного дерева при последовательной вставке элементов 1, 2, 3, 4, 5 и 6.
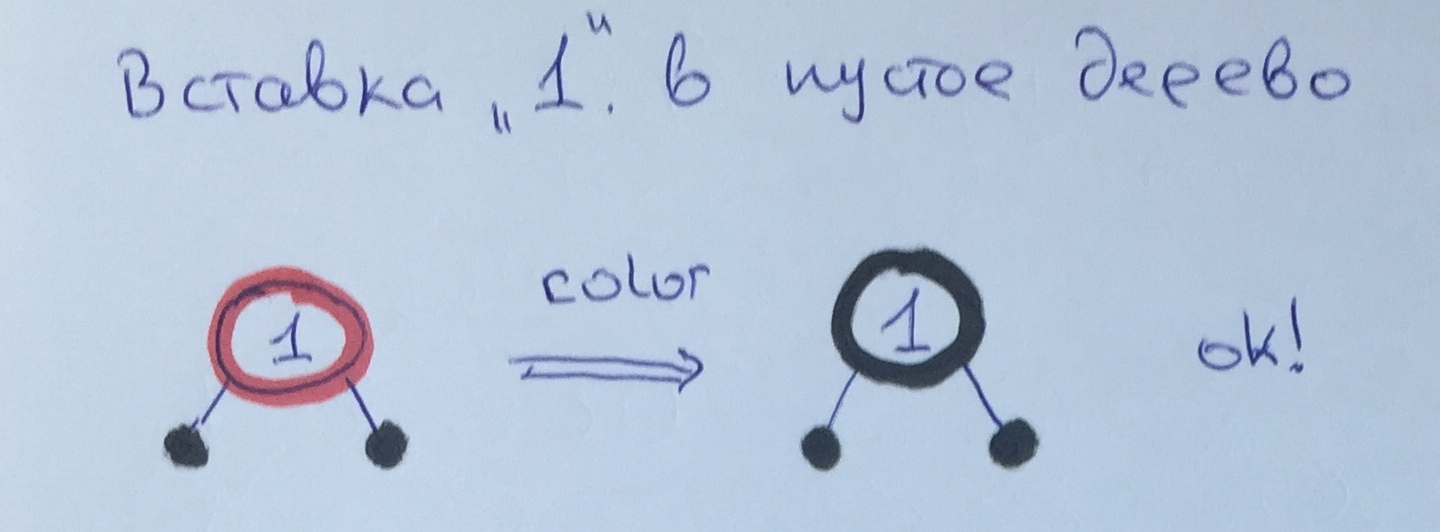
Так как элемент 1 является корнем — мы его просто перекрашиваем для выполнения 1 правила.
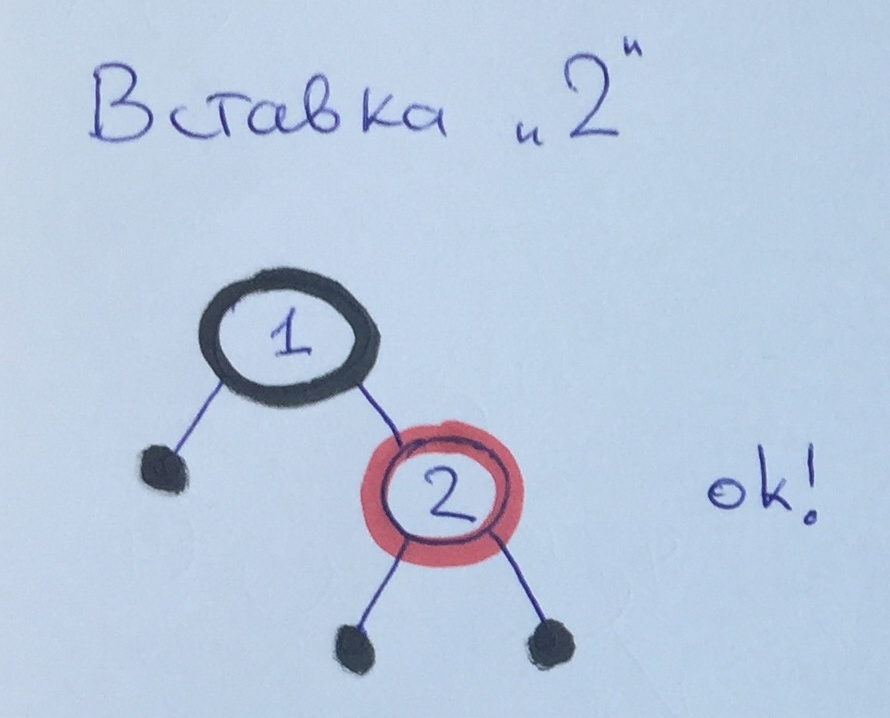
После добавления элемента 2 все правила выполняются.
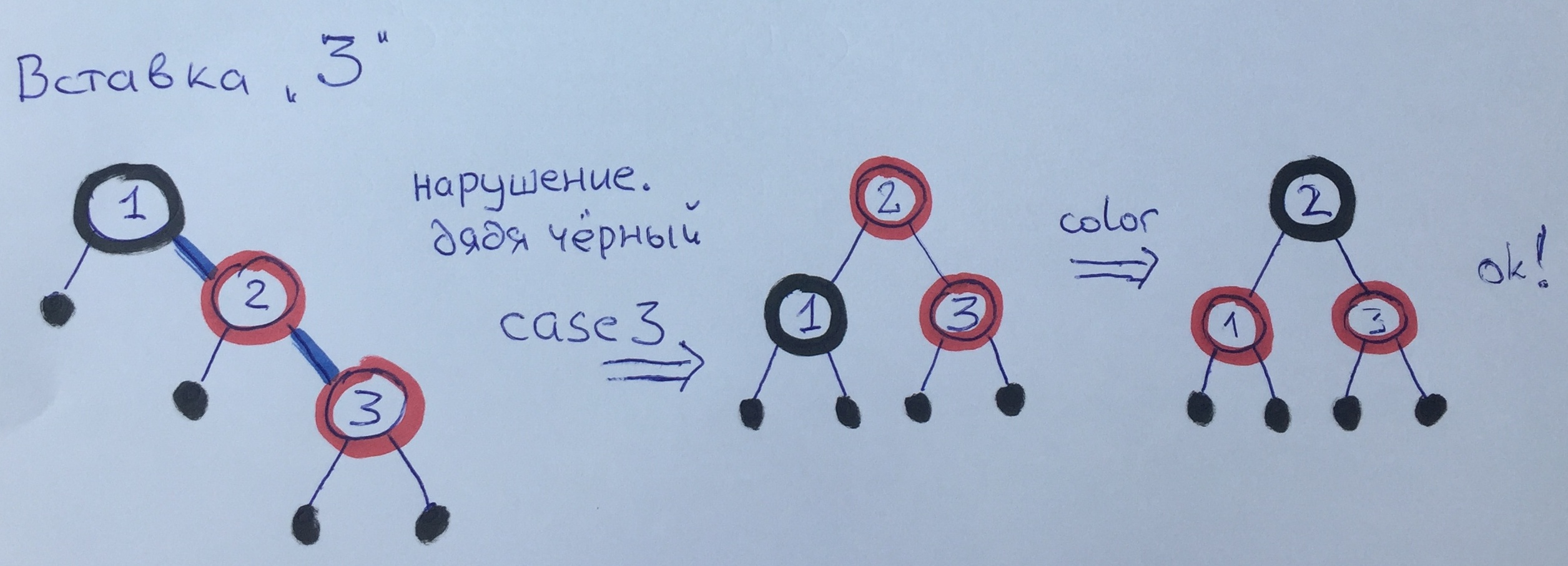
При добавлении элемента 3 у нас нарушилось 3 правило. Так как у нас дядя чёрный, а дед и отец с одной стороны, то мы применяем третий случай — делаем поворот и перекрашиваем.
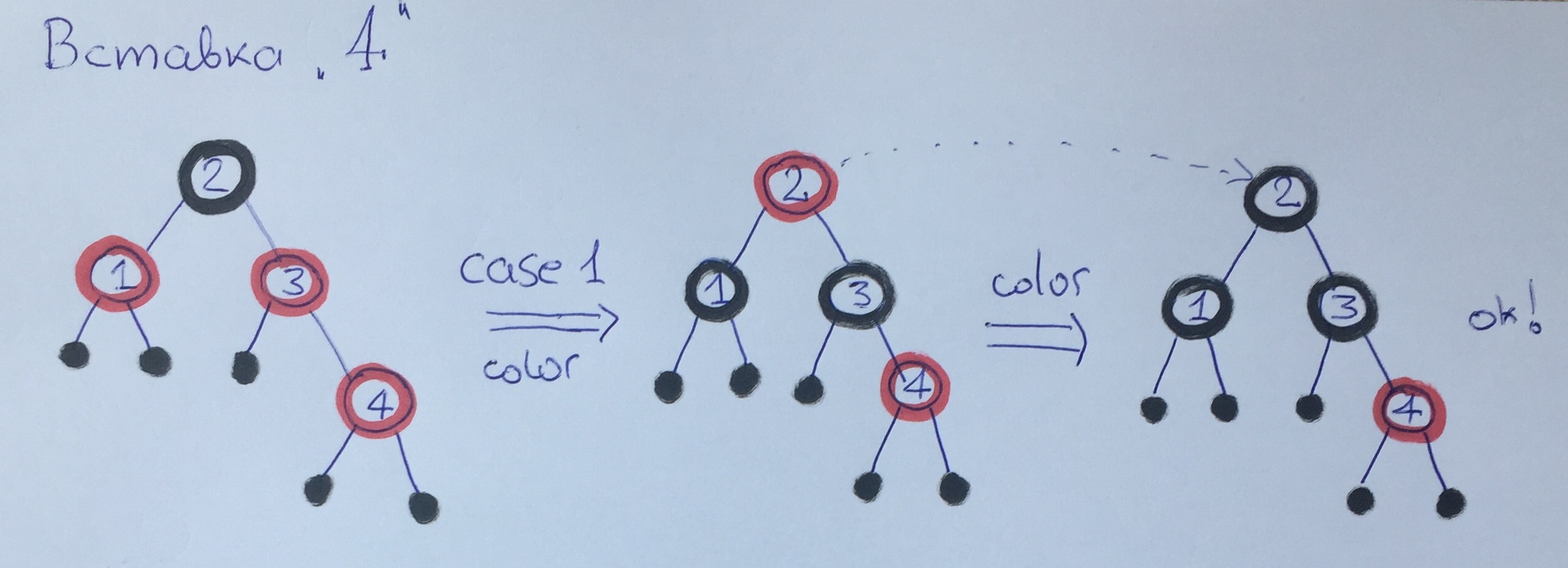
При добавлении элемента 4 у нас опять нарушается 3 правило. На этот раз дядя у нас красный, поэтому применим первый случай с перекрашиванием — чёрная высота дерева увеличится на 1. Обратите внимание. что алгоритм балансировки запускается ещё дополнительно для деда — элемента 2, который, как корень, просто перекрашивается в чёрный цвет.
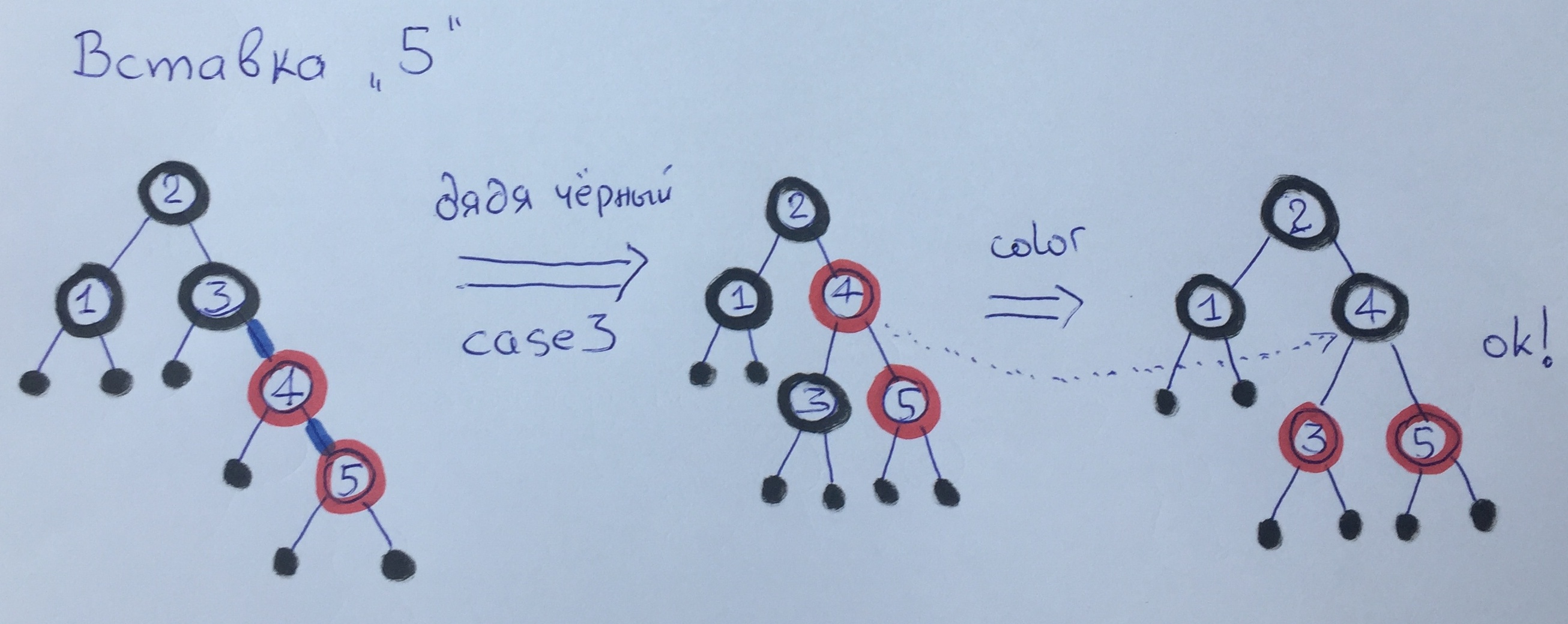
При вставке элемента 5 мы снова применяем 3 случай — делаем большой поворот и перекрашиваем вершины. Обратите внимание, что чёрная высота не изменилась.
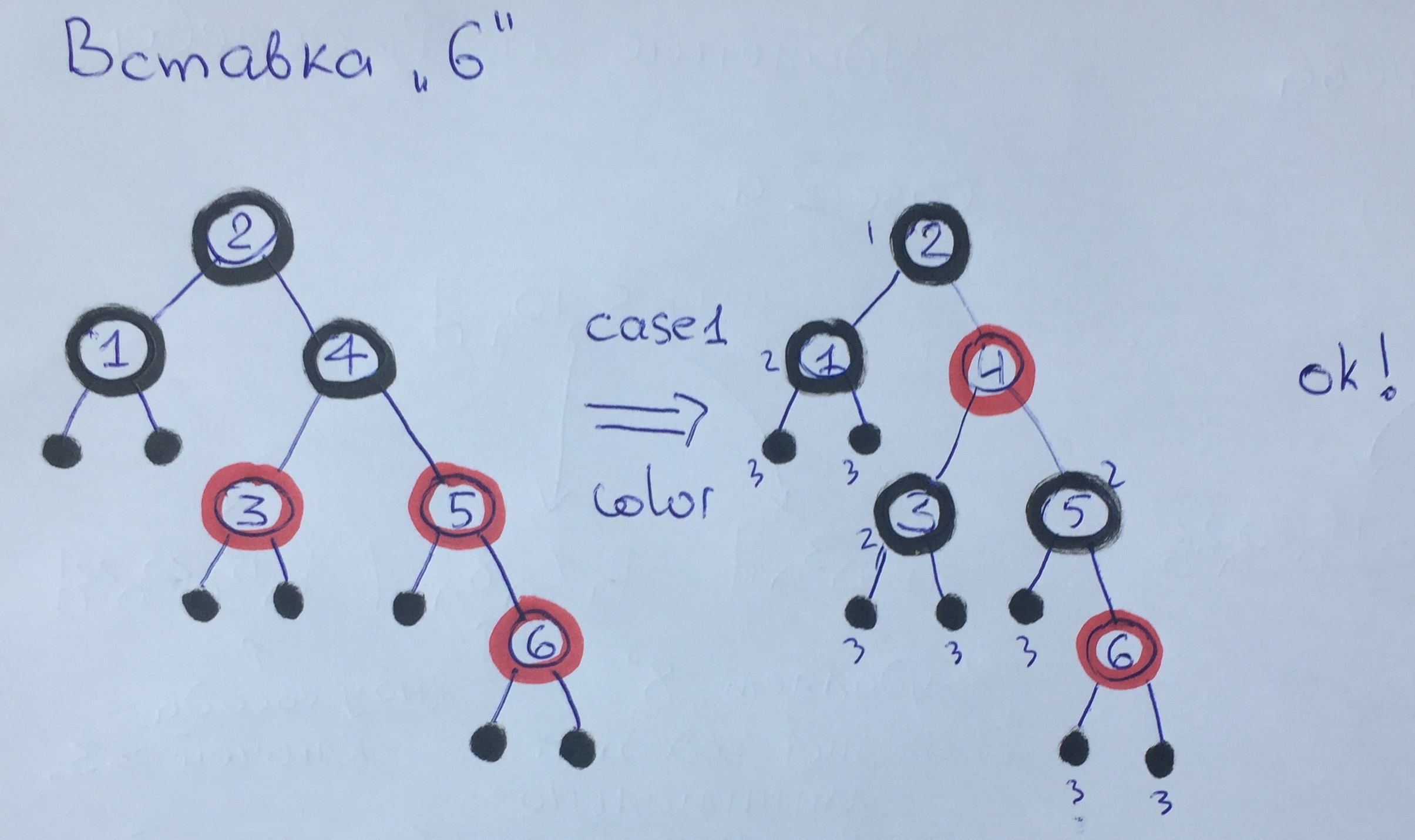
При добавлении элемента 6 мы снова нарушили 3 правило. Так как наш дядя красный, то применяем первый случай с перекрашиванием, чёрная высота не изменилась. Вызов балансировки для 4 элемента ничего не изменило в дереве, так как этот элемент не нарушает правил.
Итак, мы познакомились с вопросами балансировки красно-чёрного дерева, более подробно и с примерами алгоритмов эту тему, а также разновидности других двоичных деревьев поиска мы рассматриваем на курсе «Алгоритмы для разработчиков».
Комментариев нет:
Отправить комментарий