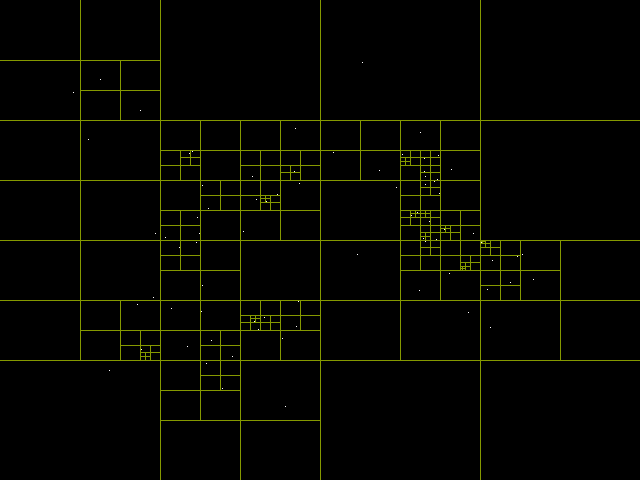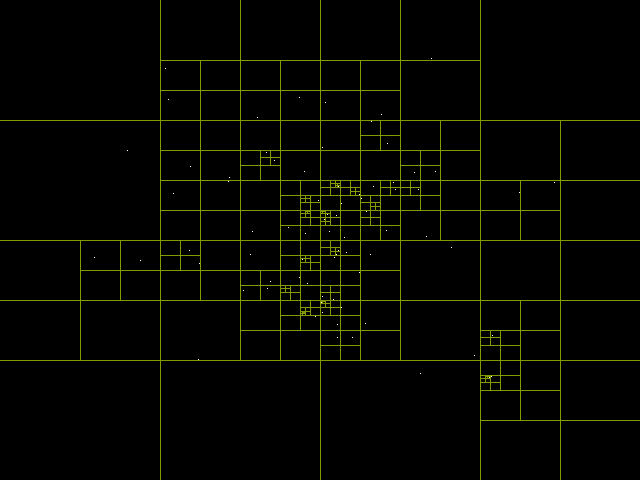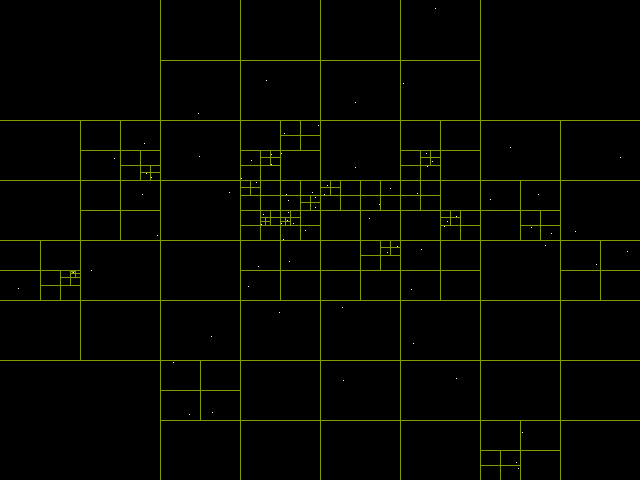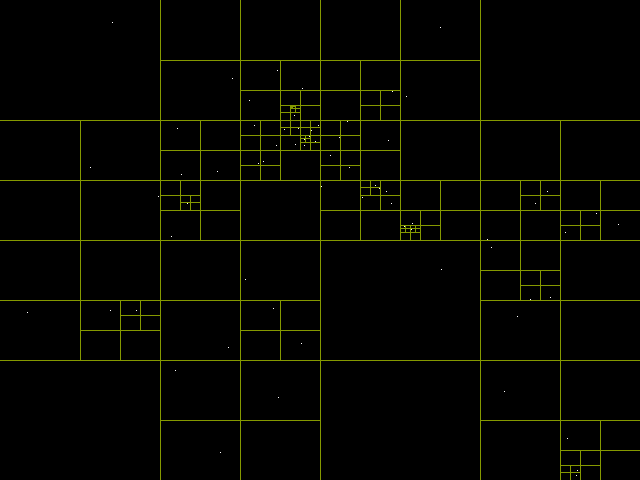
Эта неделя была короткой, в понедельник и вторник я продолжал работать над системой 2D-освещения. Остальное время я потратил на реализацию деревьев квадрантов (quadtree).
В этой статье я поделюсь своей реализацией и мыслями, возникшими в процессе её проектирования.
Во-первых, мне нужно сказать, почему я решил реализовать дерево квадрантов.
Quadtree — это структура данных разбиения пространства. Её новное преимущество по сравнению с другими структурами данных заключается в адаптивности. Оно обеспечивает хорошую производительность при вставке, удалении и поиске. То есть мы можем использовать это дерево в динамическом контексте, где данные часто меняются. Более того, эту структуру довольно легко понять и реализовать.
Если разбиение пространства для вас новая тема, то рекомендую прочитать эту статью Роберта Нистрома. Если вы хотите более подробно узнать о деревьях квадрантов, то прочитайте эту или эту статьи.
В моей игре есть области, в которых использование quadtree мгновенно оправдывает себя:
- При распознавании коллизий дерево квадрантов намного эффективнее, чем способ грубого перебора (brute-force) (тестирование всех пар). Но это не самый эффективный подход, обзор различных методик и бенчмарки можно изучить в этой статье. Тем не менее, для первой версии своего физического движка я использую его. Возможно, позже при необходимости я выберу более специализированный алгоритм.
- В графе сцены при выполнении отсечения я могу использовать quadtree для поиска всех видимых узлов.
- В системе освещения можно использовать quadtree для нахождения стен, пересекающих полигон видимости источника света.
- В системе ИИ можно использовать quadtree для поиска всех объектов или врагов, находящихся близко к сущности.
- И так далее...
Как вы можете понять, деревья квадрантов довольно универсальны. Они будут хорошим пополнением в вашем инструментарии.
Весь показанный в статье код можно найти на GitHub.
Прежде чем детализировать код quadtree, нам потребуются небольшие классы для геометрических примитивов: класс
Vector2 для задания точек и класс Box для задания прямоугольников. Оба будут шаблонными.
Vector2
Класс
Vector2 минималистичен. Он содержит только конструкторы, а также операторы + и /. Это всё, что нам потребуется:
template<typename T>
class Vector2
{
public:
T x;
T y;
constexpr Vector2<T>(T X = 0, T Y = 0) noexcept : x(X), y(Y)
{
}
constexpr Vector2<T>& operator+=(const Vector2<T>& other) noexcept
{
x += other.x;
y += other.y;
return *this;
}
constexpr Vector2<T>& operator/=(T t) noexcept
{
x /= t;
y /= t;
return *this;
}
};
template<typename T>
constexpr Vector2<T> operator+(Vector2<T> lhs, const Vector2<T>& rhs) noexcept
{
lhs += rhs;
return lhs;
}
template<typename T>
constexpr Vector2<T> operator/(Vector2<T> vec, T t) noexcept
{
vec /= t;
return vec;
}Box
Класс
Box ненамного сложнее:
template<typename T>
class Box
{
public:
T left;
T top;
T width; // Must be positive
T height; // Must be positive
constexpr Box(T Left = 0, T Top = 0, T Width = 0, T Height = 0) noexcept :
left(Left), top(Top), width(Width), height(Height)
{
}
constexpr Box(const Vector2<T>& position, const Vector2<T>& size) noexcept :
left(position.x), top(position.y), width(size.x), height(size.y)
{
}
constexpr T getRight() const noexcept
{
return left + width;
}
constexpr T getBottom() const noexcept
{
return top + height;
}
constexpr Vector2<T> getTopLeft() const noexcept
{
return Vector2<T>(left, top);
}
constexpr Vector2<T> getCenter() const noexcept
{
return Vector2<T>(left + width / 2, top + height / 2);
}
constexpr Vector2<T> getSize() const noexcept
{
return Vector2<T>(width, height);
}
constexpr bool contains(const Box<T>& box) const noexcept
{
return left <= box.left && box.getRight() <= getRight() &&
top <= box.top && box.getBottom() <= getBottom();
}
constexpr bool intersects(const Box<T>& box) const noexcept
{
return !(left >= box.getRight() || getRight() <= box.left ||
top >= box.getBottom() || getBottom() <= box.top);
}
};Он содержит несколько полезных геттеров.
Интереснее то, что он содержит метод contains, проверяющий, находится ли прямоугольник внутри другого, и метод intersects, проверяющий, пересекается ли прямоугольник с другим.
Мы будем использовать contains при вставке и удалении, а intersects — при распознавании пересечений.
Вот скелет класса
Quadtree:
template<typename T, typename GetBox, typename Equal = std::equal_to<T>, typename Float = float>
class Quadtree
{
static_assert(std::is_convertible_v<std::invoke_result_t<GetBox, const T&>, Box<Float>>,
"GetBox must be a callable of signature Box<Float>(const T&)");
static_assert(std::is_convertible_v<std::invoke_result_t<Equal, const T&, const T&>, bool>,
"Equal must be a callable of signature bool(const T&, const T&)");
static_assert(std::is_arithmetic_v<Float>);
public:
Quadtree(const Box<Float>& box, const GetBox& getBox = GetBox(),
const Equal& equal = Equal()) :
mBox(box), mRoot(std::make_unique<Node>()), mGetBox(getBox), mEqual(equal)
{
}
private:
static constexpr auto Threshold = std::size_t(16);
static constexpr auto MaxDepth = std::size_t(8);
struct Node
{
std::array<std::unique_ptr<Node>, 4> children;
std::vector<T> values;
};
Box<Float> mBox;
std::unique_ptr<Node> mRoot;
GetBox mGetBox;
Equal mEqual;
bool isLeaf(const Node* node) const
{
return !static_cast<bool>(node->children[0]);
}
};Как можно заметить,
Quadtree — это класс-шаблон. Это позволит нам использовать класс для различных целей, о которых я говорил в начале.
Параметры шаблона:
T: тип значений, которые будут содержаться в quadtree.Tдолжен быть лёгким классом, потому что он будет хранится внутри quadtree. В идеале это должен быть указатель или небольшая простая структура данных (POD).GetBox: тип вызываемого объекта, который будет получать значение на входе и возвращать прямоугольник.Equal: тип вызываемого объекта для проверки равенства двух значений. По умолчанию мы используем стандартный оператор равенства.Float: арифметический тип, используемый в вычислениях. По умолчанию мы используемfloat.
В начале определения класса есть три статических допущения (assertion) для проверки правильности параметров шаблона.
Давайте взглянем на определение узла. Узел просто хранит указатели на свои четыре дочерних узла и список содержащихся в нём значений. Мы не храним в нём его ограничивающий прямоугольник или глубину, они будут вычисляться на лету.
Я провёл бенчмарки обоих подходов (с сохранением прямоугольника с глубиной и без сохранения) и не обнаружил снижения производительности при вычислении их на лету. Более того, так экономится немного памяти.
Чтобы иметь возможность отличать внутренний узел от листа, существует метод isLeaf. Он просто проверяет, что первый дочерний элемент не равен null. Так как null являются или все дочерние узлы, или ни один из них, достаточно проверять только первый.
Теперь мы можем рассмотреть переменные-члены Quadtree:
mBox— это глобальный ограничивающий прямоугольник. Все вставляемые в quadtree значения должны содержаться внутри него.mRoot— корень quadtree.mGetBox— вызываемый объект, который мы будем использовать для получения прямоугольника из значения.mEqual— вызываемый объект, который мы будем использовать для проверки равенства двух значений.
Конструктор просто задаёт
mBox, mGetBox и mEqual, а также создаёт корневой узел.
Последние два параметра, о которых мы ещё не говорили — это Threshold и MaxDepth. Threshold — максимальное количество значений, которое может содержать узел, прежде чем мы его разделим. MaxDepth — это максимальная глубина узла, мы прекращаем пытаться разделить узлы, которые находятся на MaxDepth, потому что если разделять слишком много, это может помешать производительности. Я задал этим константам разумные значения, подходящие для большинства случаев. Можете попробовать оптимизировать их под свою конфигурацию.
Теперь мы готовы приступить к более интересным операциям.
Прежде чем я покажу код вставки, нам нужно обсудить то, какие узлы будут содержать значения. Существует две стратегии:
- Значения хранятся только в листьях. Так как ограничивающий прямоугольник значения может взаимодействовать с несколькими листьями, значение будет храниться во всех этих листьях.
- Значения могут храниться во всех узлах. Мы сохраняем значение в наименьший узел, который полностью содержит его ограничивающий прямоугольник.
Если ограничивающие прямоугольники малы и имеют примерно одинаковый размер, то при поиске пересечений более эффективна первая стратегия. Однако, если существуют большие прямоугольники, могут возникать вырожденные случаи, при которых производительность будет очень плохой. Например, если мы вставим значение, прямоугольник которого находится в глобальном ограничивающем прямоугольнике, то оно будет добавлено во все листья. А если мы вставим
Threshold для таких значений, то все узлы будут разделяться, пока не достигнут MaxDepth и значения не окажутся во всех листьях. Следовательно, quadtree будет содержать значений, а это… много.
Более того, при первой стратегии вставка и удаление будут немного медленнее, потому что нам придётся вставлять (или удалять) все узлы, пересекающие значение.
Поэтому я буду использовать вторую стратегию, в которой не бывает вырожденных случаев. Так как я планирую применять quadtree в различных контекстах, это будет удобнее. Кроме того, такая стратегия больше подходит для динамических контекстов, в которых для обновления значений выполняется множество вставок и удалений, например, в физическом движке, где сущности перемещаются.
Чтобы узнать, в какой узел мы будем вставлять или удалять значение, воспользуемся двумя вспомогательными функциями.
Первая, computeBox, вычисляет прямоугольник дочернего узла по прямоугольнику родительского узла и индекс его квадранта.
Box<Float> computeBox(const Box<Float>& box, int i) const
{
auto origin = box.getTopLeft();
auto childSize = box.getSize() / static_cast<Float>(2);
switch (i)
{
// North West
case 0:
return Box<Float>(origin, childSize);
// Norst East
case 1:
return Box<Float>(Vector2<Float>(origin.x + childSize.x, origin.y), childSize);
// South West
case 2:
return Box<Float>(Vector2<Float>(origin.x, origin.y + childSize.y), childSize);
// South East
case 3:
return Box<Float>(origin + childSize, childSize);
default:
assert(false && "Invalid child index");
return Box<Float>();
}
}Вторая,
getQuadrant, возвращает квадрант, в котором находится значение:
int getQuadrant(const Box<Float>& nodeBox, const Box<Float>& valueBox) const
{
auto center = nodeBox.getCenter();
// West
if (valueBox.getRight() < center.x)
{
// North West
if (valueBox.getBottom() < center.y)
return 0;
// South West
else if (valueBox.top >= center.y)
return 2;
// Not contained in any quadrant
else
return -1;
}
// East
else if (valueBox.left >= center.x)
{
// North East
if (valueBox.getBottom() < center.y)
return 1;
// South East
else if (valueBox.top >= center.y)
return 3;
// Not contained in any quadrant
else
return -1;
}
// Not contained in any quadrant
else
return -1;
}Она возвращает
-1, если оно не содержится ни в одном из квадрантов.
Теперь мы готовы рассмотреть методы вставки и удаления.
Вставка
Метод
add просто вызывает приватный вспомогательный метод:
void add(const T& value)
{
add(mRoot.get(), 0, mBox, value);
}Вот код вспомогательного метода:
void add(Node* node, std::size_t depth, const Box<Float>& box, const T& value)
{
assert(node != nullptr);
assert(box.contains(mGetBox(value)));
if (isLeaf(node))
{
// Insert the value in this node if possible
if (depth >= MaxDepth || node->values.size() < Threshold)
node->values.push_back(value);
// Otherwise, we split and we try again
else
{
split(node, box);
add(node, depth, box, value);
}
}
else
{
auto i = getQuadrant(box, mGetBox(value));
// Add the value in a child if the value is entirely contained in it
if (i != -1)
add(node->children[static_cast<std::size_t>(i)].get(), depth + 1, computeBox(box, i), value);
// Otherwise, we add the value in the current node
else
node->values.push_back(value);
}
}В начале расположена пара допущений, проверяющих, что мы не делаем ничего нелогичного, например, не вставляем значение в узел, не содержащий его ограничивающий прямоугольник.
Затем, если узел является листом, и мы можем вставить в него новое значение, т.е. мы не достигли MaxDepth или Threshold, выполняем вставку. В противном случае мы разделяем этот узел и пробуем снова.
Если узел внутренний, то вычисляем квадрант, в котором содержится ограничивающий прямоугольник значения. Если он полностью содержится в дочернем узле, выполняем рекурсивный вызов. В противном случае, выполняем вставку в этот узел.
Вот процедура разделения:
void split(Node* node, const Box<Float>& box)
{
assert(node != nullptr);
assert(isLeaf(node) && "Only leaves can be split");
// Create children
for (auto& child : node->children)
child = std::make_unique<Node>();
// Assign values to children
auto newValues = std::vector<T>(); // New values for this node
for (const auto& value : node->values)
{
auto i = getQuadrant(box, mGetBox(value));
if (i != -1)
node->children[static_cast<std::size_t>(i)]->values.push_back(value);
else
newValues.push_back(value);
}
node->values = std::move(newValues);
}Мы создаём четыре дочерних узла, а затем для каждого значения родительского узла решаем, в каком узле (дочернем или родительском) должно храниться значение.
Удаление
Метод
remove тоже просто вызывает вспомогательный метод:
void remove(const T& value)
{
remove(mRoot.get(), nullptr, mBox, value);
}Вот код вспомогательного метода, он очень похож на код вставки:
void remove(Node* node, Node* parent, const Box<Float>& box, const T& value)
{
assert(node != nullptr);
assert(box.contains(mGetBox(value)));
if (isLeaf(node))
{
// Remove the value from node
removeValue(node, value);
// Try to merge the parent
if (parent != nullptr)
tryMerge(parent);
}
else
{
// Remove the value in a child if the value is entirely contained in it
auto i = getQuadrant(box, mGetBox(value));
if (i != -1)
remove(node->children[static_cast<std::size_t>(i)].get(), node, computeBox(box, i), value);
// Otherwise, we remove the value from the current node
else
removeValue(node, value);
}
}Если текущий узел является листом, то мы удаляем значение из списка значений текущего узла
и пытаемся объединить этот узел с сестринскими узлами и его родителем. В противном случае, мы определяем, в каком квадранте находится ограничивающий прямоугольник значения. Если он полностью содержится в дочернем узле, то выполняем рекурсивный вызов. В противном случае, удаляем из значений текущего узла.
Так как нас не волнует порядок хранимых в узле значений, при стирании я использую небольшую оптимизацию: просто меняю стираемое значение с последним и удаляю его:
void removeValue(Node* node, const T& value)
{
// Find the value in node->values
auto it = std::find_if(std::begin(node->values), std::end(node->values),
[this, &value](const auto& rhs){ return mEqual(value, rhs); });
assert(it != std::end(node->values) && "Trying to remove a value that is not present in the node");
// Swap with the last element and pop back
*it = std::move(node->values.back());
node->values.pop_back();
}Также нам нужно взглянуть на
tryMerge:
void tryMerge(Node* node)
{
assert(node != nullptr);
assert(!isLeaf(node) && "Only interior nodes can be merged");
auto nbValues = node->values.size();
for (const auto& child : node->children)
{
if (!isLeaf(child.get()))
return;
nbValues += child->values.size();
}
if (nbValues <= Threshold)
{
node->values.reserve(nbValues);
// Merge the values of all the children
for (const auto& child : node->children)
{
for (const auto& value : child->values)
node->values.push_back(value);
}
// Remove the children
for (auto& child : node->children)
child.reset();
}
}tryMerge проверяет, что все дочерние узлы являются листьями и что общее количество его значений и значений дочерних узлов меньше, чем threshold. Если это так, то мы копируем все значения из дочерних узлов в текущий узел и удаляем дочерние узлы.Пересечение с прямоугольником
Наконец, мы добрались до самого интересного: до поиска пересечений. Первый способ применения — получение всех значений, пересекающих заданный прямоугольник. Например, это нужно для выполнения отсечения.
Этим будет заниматься query:
std::vector<T> query(const Box<Float>& box) const
{
auto values = std::vector<T>();
query(mRoot.get(), mBox, box, values);
return values;
}В этом методе мы просто выделяем
std::vector, который будет содержать значения, пересекающие ограничивающий прямоугольник, и вызываем вспомогательный метод:
void query(Node* node, const Box<Float>& box, const Box<Float>& queryBox, std::vector<T>& values) const
{
assert(node != nullptr);
assert(queryBox.intersects(box));
for (const auto& value : node->values)
{
if (queryBox.intersects(mGetBox(value)))
values.push_back(value);
}
if (!isLeaf(node))
{
for (auto i = std::size_t(0); i < node->children.size(); ++i)
{
auto childBox = computeBox(box, static_cast<int>(i));
if (queryBox.intersects(childBox))
query(node->children[i].get(), childBox, queryBox, values);
}
}
}Сначала мы складываем все значения, хранящиеся в текущем узле, которые пересекаются с запрашиваемым прямоугольником. Затем, если текущий узел является внутренним, мы выполняем рекурсивный вызов для каждого дочернего узла, чей ограничивающий прямоугольник пересекается с запрашиваемым прямоугольником.
Все попарные пересечения
Второй поддерживаемый способ применения — поиск всех хранящихся в дереве квадрантов пар значений, которые пересекаются. Это особенно полезно при создании физического движка. Данную задачу можно решить при помощи метода
query. И в самом деле, мы можем вызвать query для ограничивающего прямоугольника всех значений. Однако, это можно сделать более эффективно, добавляя только по одному пересечению для пары (при помощи query мы будем находить их дважды).
Чтобы реализовать это, нам нужно учесть, что пересечение может происходить только
- между двумя значениями, хранящимися в одном узле
или
- между значением, хранящимся в узле, и ещё одним значением, хранящемся в потомке этого узла.
Благодаря этому мы должны проверять только пересечение между:
- значением и следующими значениями, хранящимися в том же узле
и
- значением и значениями, хранящимися в потомке.
Таким образом, мы точно не будем дважды сообщать об одном пересечении.
Вот код findAllIntersections:
std::vector<std::pair<T, T>> findAllIntersections() const
{
auto intersections = std::vector<std::pair<T, T>>();
findAllIntersections(mRoot.get(), intersections);
return intersections;
}Мы снова просто выделяем
std::vector для хранения пересечений и вызываем вспомогательную функцию:
void findAllIntersections(Node* node, std::vector<std::pair<T, T>>& intersections) const
{
// Find intersections between values stored in this node
// Make sure to not report the same intersection twice
for (auto i = std::size_t(0); i < node->values.size(); ++i)
{
for (auto j = std::size_t(0); j < i; ++j)
{
if (mGetBox(node->values[i]).intersects(mGetBox(node->values[j])))
intersections.emplace_back(node->values[i], node->values[j]);
}
}
if (!isLeaf(node))
{
// Values in this node can intersect values in descendants
for (const auto& child : node->children)
{
for (const auto& value : node->values)
findIntersectionsInDescendants(child.get(), value, intersections);
}
// Find intersections in children
for (const auto& child : node->children)
findAllIntersections(child.get(), intersections);
}
}На первом этапе проверяются пересечения между значениями, хранящимися в текущем узле. Затем, если текущий узел является внутренним, при помощи
findIntersectionInDescendants проверяются пересечения между значениями, хранящимися в этом узле и значениями, хранящимися в его потомках. Наконец, мы выполняем рекурсивные вызовы.
findIntersectionsInDescendants рекурсивно находит пересечения между заданным значением и всеми значениями, хранящимися в поддереве:
void findIntersectionsInDescendants(Node* node, const T& value, std::vector<std::pair<T, T>>& intersections) const
{
// Test against the values stored in this node
for (const auto& other : node->values)
{
if (mGetBox(value).intersects(mGetBox(other)))
intersections.emplace_back(value, other);
}
// Test against values stored into descendants of this node
if (!isLeaf(node))
{
for (const auto& child : node->children)
findIntersectionsInDescendants(child.get(), value, intersections);
}
}Вот и всё! Повторюсь, весь код выложен на GitHub.
Если вы хотите больше узнать о распознавании коллизий и структурах данных разбиения пространства, то рекомендую прочитать книгу Кристера Эриксона Real-Time Collision Detection. В ней глубоко раскрыто множество тем и при этом книга написана очень понятным языком. Более того, главы можно читать по отдельности. Это отличный справочный источник.
На этом работа с распознаванием коллизий завершена. Однако оно является только половиной физического движка. Вторая половина — это разрешение коллизий.
Комментариев нет:
Отправить комментарий