Большинство найденных объяснений было слишком техническим, неполным или чересчур сложным для моего понимания, поэтому я решил попробовать объяснить собранную мной информацию. Я понимаю, что эти объяснения могут быть неполными или не совсем точными, но всё равно попробую.
Первые созданные человеком 3D-модели выглядели примерно так:

Это замечательно, но у такой модели есть очевидное ограничение: она выглядит слишком полигональной.
Наиболее очевидное решение: добавить больше полигонов, сделав поверхность более равномерной и гладкой, вплоть до того, чтобы полигоны казались единой гладкой поверхностью. Но оказывается, для того, чтобы сделать поверхности наподобие сфер гладкими, нужно огромное количество полигонов (особенно сегодня).

Требовалось другое решение, и так были изобретены нормали. (Всё происходило не совсем так, но так проще объяснять и понимать.)
Давайте проследим за линией из центра полигона, перпендикулярной его поверхности. Мы дадим этой линии очень непривычное название: нормаль. Цель нормали — контролировать, куда указывает поверхность, чтобы когда свет отразиться от этой поверхности, она могла использовать нормаль для вычисления получившегося отражения. Когда свет падает на полигон, мы сравниваем угол луча света с нормалью полигона. Луч отражается под тем же углом относительно направления нормали:

Другими словами, отражение света будет симметрично относительно нормали полигона. Именно так работает большинство отражений в реальном мире. По умолчанию лучи света отражаются от всех полигонов совершенно перпендикулярно к их поверхности (как должны это делать в реальной жизни), потому что нормали полигона по умолчанию перпендикулярны к поверхности полигона. Если в нормалях будут пробелы, то мы увидим их как отдельные поверхности, поскольку свет отразится в одном или другом направлении.
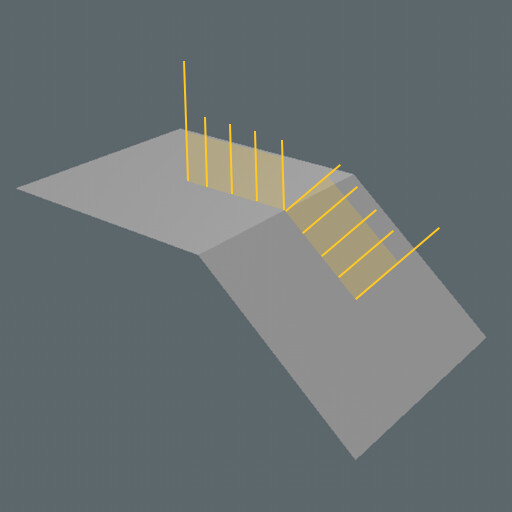
Если две грани соединены, то мы можем попросить компьютер сгладить переход между нормалью одного полигона к другому, чтобы нормали постепенно выстраивались в соответствии с ближайшей нормалью полигона. Таким образом, когда свет попадёт ровно в центр одного полигона, то он отразится прямо, в соответствии с направлением нормали. Но между полигонами это направление нормали сглаживается, изменяя отражение света.

Мы будем воспринимать переход как единую поверхность, потому что свет будет отражаться между одним и другим полигоном плавным образом, и между ними не будет пробелов. По сути, свет отражается от этих полигонов плавно, как будто у нас имеется множество полигонов.
Именно этим мы управляем, задавая smoothing groups (3ds Max, Blender) или указывая рёбра как hard или smooth (Modo, Maya): мы сообщаем программе, какие переходы между гранями должны быть плавными, а какие — жёсткими.
Вот сравнение одной сферы из 288 полигонов с жёсткими и плавными переходами:

Потенциально мы можем задать нечто вроде параллелепипеда, чтобы все его вершины имели усреднённые нормали. 3D-редактор будет стремиться сгладить его поверхность, чтобы она выглядела как единая плавная поверхность. Для 3D-редактора это вполне логично, но выглядит очень странно, потому что у нас есть объект, который очевидно должен иметь несколько отдельных поверхностей (каждая грань параллелепипеда), однако программа пытается показать их как одну плавную поверхность.

Именно поэтому в 3D-редакторах обычно есть параметр углов сглаживания: если у нас есть два связанных полигона под углом, превышающем угол сглаживания, то их переход будет плавным, а соединение полигонов под углом меньше угла сглаживания будет жёстким. Благодаря этому крутые углы между поверхностями будут отображаться как разные поверхности, как это и бывает в реальном мире.
Итак, мы использовали нормали для контроля над переходами между гранями модели, но можно пойти ещё дальше.
Так как мы меняем способ отражения света от объекта, можно также сделать так, чтобы очень простой объект отражал свет, как сложный. Это называется картой нормалей. Мы используем текстуру для изменения направления света, отражающегося от 3D-объекта, заставляя его выглядеть сложнее, чем он есть на самом деле.
Примером из реального мира могут служить голограммы, которые раньше вручали в подарок при покупке картофельных чипсов (по крайней мере, у нас, в Испании). Они совершенно плоские, но отражают свет так, как бы это делал 3D-объект, благодаря чему становятся сложнее, чем на самом деле. В мире 3D-графики это работает даже лучше, но всё равно имеет свои ограничения (поскольку поверхность остаётся плоской).
Хоть мы и применяем нормали полигонов для реализации какой-то чёрной магии, на самом деле мы не контролируем сглаживание поверхности модели при помощи нормалей полигонов. Мы используем нормали вершин для контроля сглаживания нормалей. По сути, идея та же, но немного более сложная.
С каждой вершиной может быть связано одна или несколько нормалей. Если она имеет одну нормаль, то можно назвать её усреднённой нормалью вершины, а если несколько — то разделённой нормалью вершины.
Давайте возьмём два полигона, соединённых ребром. Если переход между двумя гранями плавный (если мы указали его как плавный в Maya/Modo, или обе имеют одинаковую smoothing group в Max/Blender), то каждая вершина имеет одну нормаль, которая является средней нормалей полигонов (поэтому она и называется усреднённой нормалью вершины). Важное примечание: до недавнего времени каждый 3D-редактор использовал собственный способ вычисления усреднённых нормалей вершин, то есть карты нормалей, вычисленные в одной программе, в другой могли выглядеть совершенно иначе. Подробнее об этом я расскажу во второй части туториала.

Если переход жёсткий (hard edge или разные smoothing groups), то каждая вершина имеет несколько нормалей: по одной для каждой соединённой вершины, выровненной по их нормалям. При этом между нормалями образуется пробел, который выглядит как две разные поверхности. Именно это называется разделённой нормалью вершины.


Как вы могли догадаться, контроль нормалей вершин очень важен, если мы хотим контролировать карты нормалей. К счастью, нам не обязательно изменять нормали напрямую или даже видеть их, но понимание того, как это работает, поможет вам понять, почему мы выполняем работу именно так и больше разбираться в проблемах, с которыми мы можем встретиться.
При запекании карты нормалей мы по сути говорим программе изменить направление, которому следуют нормали lowpoly-модели, так, чтобы они соответствовали направлению в highpoly-модели; поэтому lowpoly-модель будет отражать свет так же, как highpoly. Вся эта информация хранится в текстуре под названием «карта нормалей». Давайте рассмотрим пример.
Допустим, у нас есть вот такая низкополигональная модель (lowpoly). Плоская поверхность с четырьмя вершинами и настроенными UV, которые программа запекания будет использовать для создания карты нормалей.

И она должна получить информацию о нормалях от этой высокополигональной (highpoly) модели, нормали которой сложнее.

Помните, что мы переносим только информацию о нормалях, то есть UV, материал, топология, преобразования и т.п. к делу не относятся. Проверенное правило: если highpoly-модель выглядит хорошо, то её нормали тоже хороши и вполне должны подходить для запекания.
Программа запекания берёт lowpoly-модель и испускает лучи, следуя по направлениям нормалей lowpoly (именно поэтому нам нужно контролировать нормали lowpoly). Эти лучи имеют ограниченную длину чтобы не получать информацию нормалей от далёких граней (обычно это расстояние называется bake distance или cage distance). Когда эти лучи сталкиваются с highpoly, программа запекания вычисляет, как отразить эти лучи, чтобы они следовали по направлению нормалей highpoly, и сохраняет эту информацию в карту нормалей.
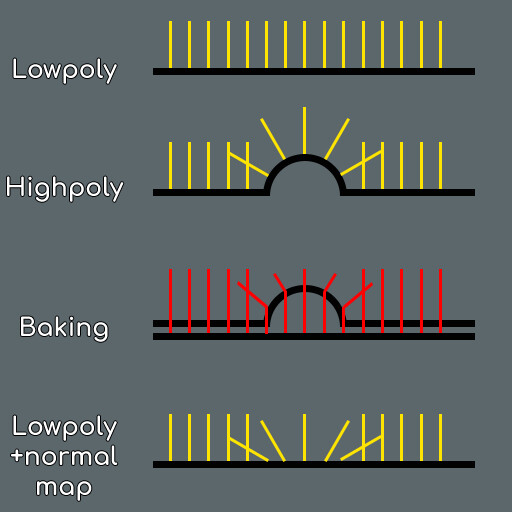
Вот результат запекания для нашего примера:

У нас есть текстура, которую движок использует для изменения нормалей lowpoly, чтобы свет отражался от этой lowpoly-модели так же, как он отражался бы от highpoly-версии. Не забывайте, что это только текстура, которая не влияет на силуэт lowpoly-модели (невозможно изменить способ отражения света от модели, если свет не падает на эту модель).
Хотя понятно, что можно «считать» внешний вид highpoly по внешнему виду карты нормалей, очевидно, что карты нормалей — это не обычные текстуры, потому что они хранят информацию не о цвете, а о нормалях. Также это значит, что карты нормалей нельзя рассматривать как обычные текстуры; к тому же, как мы увидим, они обладают особыми параметрами сжатия и гамма-коррекции.
Можно воспринимать карту нормалей как набор из трёх текстур в оттенках серого, хранящийся в одном изображении:

Первое изображение сообщает движку, как эта модель должна отражать свет, падающий справа; оно хранится в красном канале текстуры карты нормалей.
Второе изображение сообщает движку, как модель должна отражать свет, падающий снизу*; оно хранится в зелёном канале текстуры карты нормалей.
*В некоторых программах свет падает не снизу, а сверху, то есть могут быть «левосторонние» и «правосторонние» карты нормалей. Как мы увидим позже, это может вызывать некоторые проблемы.
Третье изображение сообщает движку, как модель должна отражать свет, падающий спереди; оно хранится в синем канале текстуры карты нормалей. Так как большинство объектов при освещении спереди выглядят белыми, карты нормалей обычно кажутся синеватыми.
Когда мы комбинируем все три изображения в одно, то получаем карту нормалей. Помните, что это объяснение не полностью корректно, но надеюсь, что оно позволит вам понять информацию, хранящуюся внутри карты нормалей, и лучше разобраться, что она делает.
Подведём итог:
Нормали — это векторы, которые используются для определения того, как свет отражается от поверхности. Их можно использовать для контроля над переходом между гранями (усреднением нормалей соединённых вершин для создания плавного перехода или разделением их для создания жёсткого перехода), но также их направление можно изменять, чтобы lowpoly-модель отражала свет так же, как более сложная модель.
Эта информация хранится в трёх отдельных каналах изображения, и 3D-редактор считывает её, чтобы понять, в каком направлении должна смотреть поверхность модели.
В следующей статье цикла мы поговорим о том, как можно запекать эти детали из highpoly-модели в lowpoly.
Комментариев нет:
Отправить комментарий