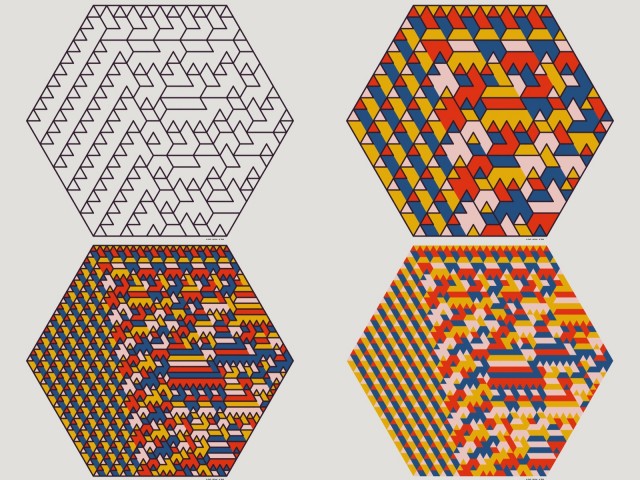
Клеточный автомат — это система, состоящая из клеток с численными значениями в сетке, а также из правил, определяющих поведение этих клеток. Многократно применяя правило к каждой клетке сетки параллельно с визуализацией сетки, часто можно получить эффект некоего эволюционирующего организма со сложным и замысловатым поведением, даже если правила относительно просты.
Клеточные автоматы имеют различные формы, виды и размерности. Наверно, самым знаменитым клеточным автоматом является конвеевская игра «Жизнь» (Conway's Game of Life, GOL). Она состоит из двухмерной сетки, в которой каждая клетка содержит двоичное значение (живая или мёртвая). Сопутствующие правила на основании состояния соседних клеток определяют, должна ли клетка быть мёртвой или живой. Правила гласят, что живая клетка умирает от одиночества, если вокруг неё меньше 2 живых клеток. Если живы больше трёх соседних клеток, она погибает от перенаселённости. Другими словами, клетка «выживает», если вокруг неё ровно 2 или 3 живых соседних клеток. Чтобы мёртвая клетка ожила, у неё должно быть ровно 3 живых соседних клеток, в противном случае она остаётся мёртвой. Пример автомата GoL, итеративно проходящий несколько состояний, показан ниже.
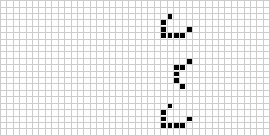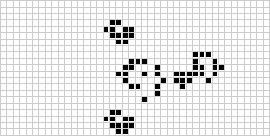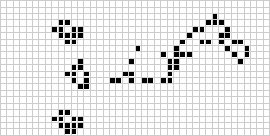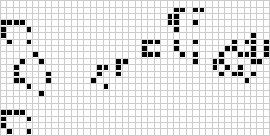
Ещё один знаменитый вариант клеточного автомата одномерен; он называется элементарным клеточным автоматом (Elementary Cellular Automaton, ECA). Именно его мы реализуем в этом посте.
Каждое состояние этого автомата хранится как одномерный массив булевых значений, и в то время, как для визуализации состояния GOL требуется два измерения, этому автомату достаточно одной строки значений. Благодаря этому для визуализации всей истории состояний этого автомата мы можем использовать два измерения (а не анимацию). Как и в случае с GOL, состояние клетки в этом автомате равно 0 или 1, но в отличие от клетки GOL, которая обновляется в зависимости от своих 8 соседей, клетка ECA обновляется на основании состояния левого соседа, правого соседа и самой себя!
Примеры правил показаны ниже: три верхних клетки являются входными данными правила, а одна нижняя — выходными данными, где чёрным обозначена 1, а белым — 0. Также мы можем увидеть паттерны, генерируемые каждым из них, когда исходным состоянием являются все 0 за исключением 1 в средней клетке.
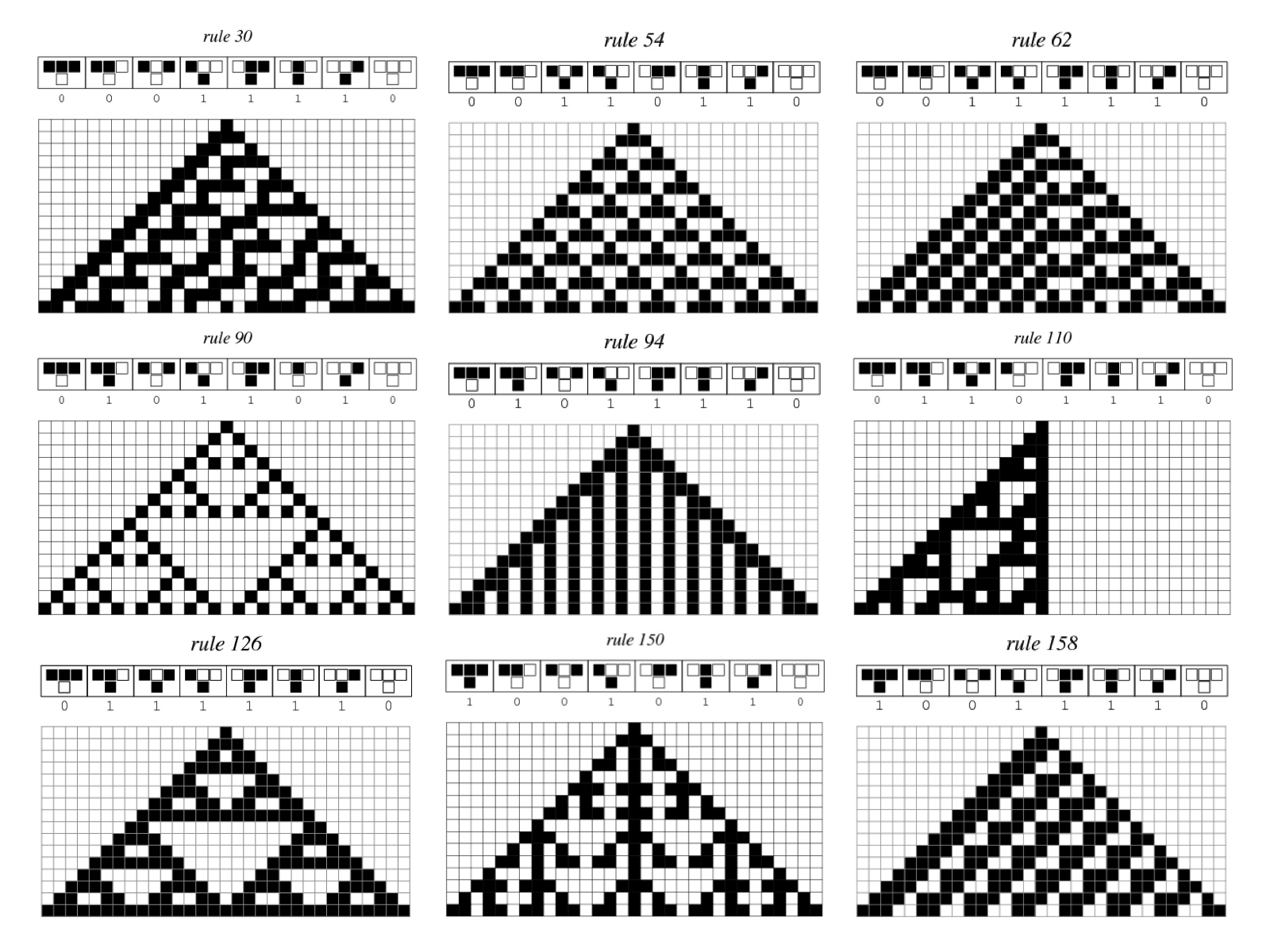
Вы можете задаться вопросом: почему представленные выше правила обозначены числами? Потому что каждое число в интервале от 0 до 255 напрямую соответствует правилу ECA, а потому эти числа используются как названия правил. Это соответствие показано ниже:
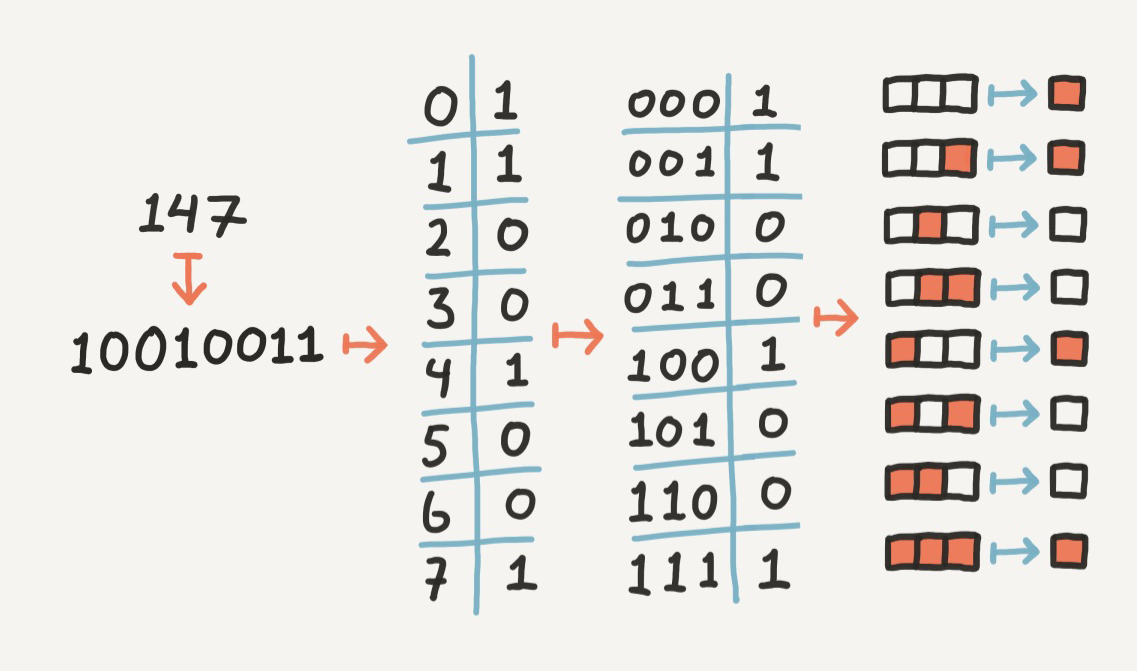
От числа к правилу
Любое число в интервале от 0 до 255 может быть представлено в двоичном виде при помощи всего 8 цифр (первая стрелка выше). Более того, мы можем дать каждой из этих цифр индекс на основании её расположения (вторая стрелка). Естественно, эти индексы находятся в интервале от 0 до 7, то есть могут быть представлены в двоичном виде при помощи всего 3 цифр (третья стрелка). Интерпретировав эти 3 цифры как входящие данные, а соответствующую цифру из исходного числа как выходные данные, мы получаем тернарную функцию, которая нам нужна (четвёртая стрелка).
Генерация правил
Давайте реализуем представленную выше интерпретацию как функцию более высокого порядка
get_rule, получающую в качестве входных данных число от 0 до 255 и возвращающую соответствующее этому числу правило ECA.
Нам нужно создать нечто подобное:
const rule30 = get_rule(30);
const output110 = rule30(1, 1, 0);В приведённом выше примере, запуск
rule30(1,1,0) скомбинирует все три двоичные значения в одно число (110 = 6) и вернёт бит в этой позиции (6) в двоичном представлении 30. Число 30 в двоичном представлении — это 00011110, поэтому функция вернёт 0 (мы считаем справа и начинаем отсчёт с 0).
Зная, что три двоичных входных переменных будут скомбинированы в одно число, давайте начнём с реализации такой функции combine.
const combine = (b1, b2, b3) => (b1 << 2) + (b2 << 1) + (b3 << 0);Выполнив сдвиг влево аргументов в соответствующие им позиции, а затем сложив три сдвинутых числа, мы получим искомую комбинацию.
Вторая важная часть функции get_rule — определение битового значения, находящегося в определённой позиции в числе. Поэтому давайте создадим функцию get_bit(num, pos), которая сможет возвращать битовое значение в заданной позиции pos в заданном числе num. Например, число 141 в двоичном виде равно 10001101, поэтому get_bit(2, 141) должна возвращать 1, а get_bit(5, 141) должна возвращать 0.
Функцию get_bit(num,pos) можно реализовать, сначала выполнив битовый сдвиг числа на pos вправо, а затем произведя побитовую операцию «И» с числом 1.
const get_bit = (num, pos) => (num >> pos) & 1;Теперь нам достаточно просто объединить эти две функции:
const get_rule = num => (b1, b2, b3) => get_bit(num, combine(b1, b2, b3));Отлично! Итак, у нас есть функция, которая для каждого числа в пределах нашего интервала даёт нам уникальное правило ECA, с которым мы можем делать, что угодно. Следующим шагом будет визуализация их в браузере.
Визуализация правил
Для визуализации автоматов в браузере мы будем использовать элемент
canvas. Элемент canvas можно создать и добавить в тело html следующим образом:
window.onload = function() {
const canvas = document.createElement('canvas');
canvas.width = 800;
canvas.height = 800;
document.body.appendChild(canvas);
};Чтобы иметь возможность взаимодействия с
canvas, нам необходим контекст. Контекст позволяет нам рисовать фигуры и линии, раскрашивать объекты и в целом перемещаться по canvas. Он предоставляется нам через метод getContext нашего canvas.
const context = canvas.getContext('2d');Параметр
'2d' относится к типу контекста, который мы будем использовать в этом примере.
Далее мы создадим функцию, которая имея контекст, правило ECA, а также некоторую информацию о масштабе и количестве клеток, рисует правило на canvas. Идея заключается в том, чтобы генерировать и рисовать сетку строка за строкой; основная часть кода выглядит примерно так:
function draw_rule(ctx, rule, scale, width, height) {
let row = initial_row(width);
for (let i = 0; i < height; i++) {
draw_row(ctx, row, scale);
row = next_row(row, rule);
}
}Мы начинаем с какого-то исходного набора клеток, являющегося текущей строкой. Эта строка, как на примерах выше, обычно содержит все нули, за исключением одной единицы в средней клетке, но также может и содержать совершенно случайную строку из 1 и 0. Мы рисуем эту строку клеток, затем при помощи правила вычисляем следующую строку значений на основании текущей строки. Затем мы просто повторяем отрисовку и вычисляем новые шаги, пока не посчитаем, что сетка достаточно высокая.
Для показанного выше фрагмента кода нам нужно реализовать три функции: initial_row, draw_row и next_row.
initial_row — это простая функция. Она создаёт массив из нулей и изменяет элемент в центре массива на единицу.
function initial_row(length) {
const initial_row = Array(length).fill(0);
initial_row[Math.floor(length / 2)] = 1;
return initial_row;
}Так как у нас уже есть функция правил, функция
next_row может состоять из одной строки. Значение каждой клетки в новой строке является результатом применения правила со значениями ближайших клеток, причём в качестве входящих данных используется старая строка.
const next_row = (row, rule) => row.map((_, i) => rule(row[i - 1], row[i], row[i + 1]));Вы заметили, что в этой строке мы сжульничали? Каждая клетка в новой строке требует входных данных от трёх других клеток, но две клетки по краям строки получают данные только от двух. Например,
next_row[0] пытается получить входящее значение от row[-1]. Это всё-таки срабатывает, потому что при попытке доступа к значениям по индексам, отсутствующим в массиве, javascript возвращает undefined, и так уж получилось, что (undefined >> [любое число]) (из функции combine) всегда возвращает 0. Это значит, что в реальности мы обрабатываем каждое значение за пределами массива, как 0.
Знаю, что это некрасиво, но скоро мы создадим на экране нечто прекрасное, так что нас можно простить.
Далее идёт функция draw_row; именно она выполняет отрисовку!
function draw_row(ctx, row, scale) {
ctx.save();
row.forEach(cell => {
ctx.fillStyle = cell === 1 ? '#000' : '#fff';
ctx.fillRect(0, 0, scale, scale);
ctx.translate(scale, 0);
});
ctx.restore();
ctx.translate(0, scale);
}Именно здесь мы сильно зависим от объекта контекста, используя из него не менее 5 различных методов. Вот их краткое перечисление и способ их применения.
fillStyleуказывает, как мы хотим заливать фигуры. Это может быть цвет, например,"#f55", а также градиент или паттерн. Мы используем этот метод, чтобы визуально отделить клетки 0 от клеток 1.fillRect(x, y, w, h)отрисовывает прямоугольник из точки (x,y) с шириной w и высотой h, залитый согласноfillStyle. Наши прямоугольники — простые квадраты, но вы можете удивиться тому, что исходная точка всех них находится в начале координат. Так получилось потому, что мы используем этот метод в сочетании сtranslate.translate(x, y)позволяет перемещать целиком систему координат. Позиция сохраняется, поэтому метод является отличной альтернативой отслеживанию разных позиций элементов. Например, вместо вычисления позиции каждой отдельной клетки сетки мы можем просто отрисовать клетку, переместиться вправо, отрисовать новую клетку, и так далее.save()иrestore()используются совместно сtranslateи другими методами преобразования координат. Мы используем их для сохранения текущей системы координат в определённой точке, чтобы позже мы могли вернуться к ней (с помощью restore). В данном случае мы сохраняем систему координат перед отрисовкой строки и перемещаем её вправо. Затем, когда мы завершили отрисовку строки и прошли весь путь вправо, координаты восстанавливаются и мы возвращаемся к исходному состоянию. Затем мы перемещаемся вниз чтобы приготовиться к отрисовке следующей строки.
Теперь у нас есть все части, необходимые для функции
draw_rule. Мы используем эту функцию в window.onload после подготовки canvas. Также мы определим необходимые нам параметры.
window.onload = function() {
const width = 1000; // Width of the canvas
const height = 500; // Height of the canvas
const cells_across = 200; // Number of cells horizontally in the grid
const cell_scale = width / cells_across; // Size of each cell
const cells_down = height / cell_scale; // Number of cells vertically in the grid
const rule = get_rule(30); // The rule to display
const canvas = document.createElement('canvas');
canvas.width = width;
canvas.height = height;
document.body.appendChild(canvas);
const context = canvas.getContext('2d');
draw_rule(context, rule, cell_scale, cells_across, cells_down);
};Мы извлекаем размеры
canvas как отдельные переменные вместе с количеством клеток по горизонтали. Затем вычисляем cell_scale и 'cells_down', чтобы сетка заполнила весь canvas, а клетки при этом оставались квадратными. Благодаря этому мы легко сможем изменять «разрешение» сетки, оставаясь в пределах canvas.

Вот и всё! Полный пример кода находится на github и на codepen:
Движемся дальше
Благодаря этой системе мы сможем исследовать одно за другим все 256 правил, или итеративно, изменяя код, или выбирая номер правила случайно при каждой загрузке страницы. Как бы то ни было, очень захватывающе изучать все эти непредсказуемые результаты в нашей контролируемой среде.
Также можно сделать исходное состояние клеток автомата случайным вместо статичных «сплошных нулей и одной единицы». Так мы получим ещё более непредсказуемые результаты. Такой вариант функции initial_row можно записать так:
function random_initial_row(width) {
return Array.from(Array(width), _ => Math.floor(Math.random() * 2));
}Ниже вы видите, насколько сильное влияние на выходные данные оказывает это изменение исходной строки.

Случайная исходная строка
И это только один из аспектов, которые вы можете изменить! Зачем ограничиваться только двумя состояниями? (Переход от 2 к 3 состояниям увеличивает количество правил с 256 до 7 625 597 484 987!) Зачем ограничиваться квадратами? Почему только 2 измерения? Почему только одно правило за раз?
Ниже показаны примеры визуализаций на основе ECA, но с альтернативной функцией draw_rule, отрисовывающей линии не квадратами, а изометрическим паттерном, а затем заливающей определяемые этими линиями области цветами. Можно даже не отображать разделительные линии и показывать только цвета.

Если пойти ещё дальше, то можно добавлять симметрии, как осевые (средняя строка), так и зеркальные (нижняя строка).

Если эти визуализации показались вам интересными, но изучите эту интерактивную песочницу, или даже лучше — начните с созданного нами кода и попробуйте придумать собственные клеточные автоматы!
Удачи!
Комментариев нет:
Отправить комментарий