[Перевод] Действительно ли использование BSP в Doom стало гениальным ходом?

Вершина технологий того времени.

В 1993 году id Software выпустила шутер от первого лица Doom, который быстро превратился в феномен. Сегодня считается, что это одна из игр, оказавших самое большое влияние за всю историю.

Десять лет спустя после выпуска Doom, в 2003 году, журналист Дэвид Кушнер опубликовал книгу об id Software под названием Masters of Doom, которая с тех пор стала каноническим описанием процесса создания Doom. Я прочитал Masters of Doom несколько лет назад и почти ничего уже не помню, но одна история из книги о ведущем программисте Джоне Кармаке сохранилась в моей памяти. Моё описание будет не совсем точным (подробнее см. ниже), но если вкратце, то на раннем этапе разработки Doom Кармак осознал, что написанный им для игры 3D-рендерер при рендеринге отдельных уровней начинал тормозить. Это было неприемлемо, потому что Doom должен был стать активной и даже бешеной игрой. Осознав, что проблема рендерера была настолько фундаментальной, что ему придётся искать более оптимальный алгоритм рендеринга, Кармак начал читать исследовательские статьи. В результате он реализовал технику под названием «двоичное разбиение пространства» (binary space partitioning, BSP), которая раньше никогда не применялась в видеоиграх, и значительно ускорил таким образом движок Doom.

Эта история о том, как Кармак применил передовые научные исследования к видеоиграм, всегда впечатляла меня. По-моему, именно благодаря этому Кармак стал такой легендарной фигурой. Он заслуживает быть известным в качестве архетипичного гениального программиста видеоигр по множеству причин, но в качестве главной мне всегда вспоминается эпизод с чтением научных статей и двоичным разбиением пространства.
Очевидно, эта история впечатляет, потому что термин «двоичное разбиение пространства» кажется чем-то сложным не только для реализации, но даже для понимания. Долгое время я предполагал, что Кармак совершил интеллектуальный рывок вперёд, но поскольку я не знал, что такое двоичное разбиение пространства, и насколько новой была эта техника, когда Кармак решил её использовать, то не был уверен полностью. Насколько гениальным было добавление двоичного разбиения пространства в Doom по шкале от Гомера Симпсона до Альберта Эйнштейна?

Также мне было интересно, откуда вообще появилось BSP и как эта идея добралась до Кармака. Поэтому этот пост будет посвящён не только Джону Кармаку и Doom, но и истории структуры данных «дерева двоичного разбиения пространства» (или BSP tree). Оказалось, что BSP tree, как и многие другие аспекты вычислительных наук, берёт своё начало в исследованиях, проводившихся для военных.

Да, всё верно: E1M1, первый уровень Doom, появился благодаря ВВС США.

Задача VSD

BSP-дерево — это решение одной из сложнейших задач в компьютерной графике. Для того, чтобы отрендерить трёхмерную сцену, рендерер должен определить, что видно и что не видно из текущей точки. Это не особо сложно, если у вас есть много времени, но уважающий себя игровой движок реального времени должен определять видимые и невидимые части мира не реже, чем 30 раз в секунду.

Эта задача часто называется задачей определения видимых поверхностей (visible surface determination, VSD). Программист Майкл Абраш, работавший с Кармаком над Quake (следующей после Doom игрой id Software), писал о задаче VSD в своей знаменитой книге Graphics Programming Black Book:

Я хочу рассказать о самой сложной, по моему мнению, задаче 3D-графики: определении видимых поверхностей (отрисовке нужной поверхности в каждом пикселе) и её близкой родственнице — задаче отсечения (culling) (максимально быстром отбрасывании невидимых полигонов для ускорения определения видимых поверхностей). Ради краткости ниже я буду обозначать аббревиатурой VSD и определение видимых поверхностей, и отсечение.

Почему я считаю VSD самой сложной 3D-задачей? Хотя проблемы растеризации, например наложение текстур, тоже являются потрясающими и важными задачами, это задачи достаточно конечного масштаба, решение которых перекладывается с появлением 3D-ускорителей на оборудование; кроме того, они масштабируются только при увеличении разрешения экрана, что вполне терпимо.

В противовес им, VSD — это ничем не ограниченная задача, и сейчас для её решения используются десятки решений. Ещё более важно то, что производительность VSD при наивном решении масштабируется в прямой зависимости от сложности сцены, которая обычно увеличивается как квадратная или кубическая функция, поэтому она быстро становится ограничивающим фактором рендеринга реалистичных миров.

Абраш писал о сложности задачи VSD в конце 90-х, несколько лет спустя после того, как Doom доказал, что обычные люди хотят иметь возможность играть в графически тяжёлые игры на своих домашних компьютерах. В начале 90-х, когда id Software только начала издавать игры, они должны были эффективно работать на не предназначенных для этого компьютерах: домашние машины были рассчитаны на работу с текстом, электронными таблицами и другими подобными приложениями. Чтобы всё добиться этой цели, компании приходилось подходить к работе с выдумкой, особенно в случае нескольких 3D-игр, опубликованных id Software до Doom. В этих играх дизайн всех уровней был ограничен таким образом, чтобы упростить решение задачи VSD.

Например, в Wolfenstein 3D — игре, которую id Software выпустила непосредственно перед Doom, каждый уровень состоял из стен, выровненных вдоль осей. Другими словами, во вселенной Wolfenstein могли быть северные/южные стены или восточные/западные стены, и никаких других. Кроме того, стены можно было размещать на фиксированных расстояниях в сетке — все коридоры имеют ширину или одну клетку сетки, или две, и т.д., но никогда 2,5 клетки. Хоть это и значило, что команда id Software могла создавать уровни, выглядящие почти одинаковыми, такое ограничение сильно упростило Кармаку написание рендерера для Wolfenstein.

Рендерер Wolfenstein решал задачу VSD, перемещением лучей (ray marching) в виртуальный мир из экрана. Обычно рендереры с использованием лучей являются raycasting-рендерерами — часто они бывают медленными, потому что решение задачи VSD в raycaster-е требует нахождения первого пересечения между лучом и каким-нибудь объектом в мире, для чего требуется много вычислений. Но поскольку в Wolfenstein все стены выстроены в сетку, единственным местом, где луч может пересечь стену, будут линии сетки. Поэтому рендереру достаточно проверять каждую из этих точек пересечений. Если рендерер начинает с проверки точки пересечения, ближайшей к точке обзора игрока, затем проверяет вторую по близости, и так далее, и заканчивает, когда столкнётся с первой стеной, то задача VSD решается наиболее тривиальным образом. Луч просто двигался вперёд из каждого пикселя, пока с чем-нибудь не столкнулся, а это очень малозатратно с точки зрения тактов процессора. А поскольку все стены имеют одинаковую высоту, нам достаточно испускать лучи для каждого столбца пикселей.

Это упрощение рендеринга сделало Wolfenstein достаточно быстрым для работы на слабых домашних ПК той эпохи, когда ещё не было специализированных графических карт. Но такой подход не сработал бы в Doom, потому что команда id решила, что в её новой игре будут такие новые элементы, как диагональные стены, лестницы и потолки с разной высотой. Ray marching больше не подходил, поэтому Кармак написал другой тип рендерера. Рендерер Wolfenstein, где луч использовался для каждого столбца пикселей, отталкивался от изображения, а рендерер Doom должен был отталкиваться от объектов. Это означало, что вместо обхода пикселей экрана и определения их цвета рендерер Doom должен был перебирать объекты в сцене и проецировать каждый из них по очереди на экран.

В таком рендерере простым способом решения задачи VSD является использование z-буфера. Каждый раз, когда мы проецируем объект на экран, выполняется проверка для каждого пикселя, который мы хотим отрисовать. Если часть объекта, который нужно нарисовать, ближе к игроку, чем уже отрисованный в пикселе объект, то мы можем переписать его информацию. В противном случае нужно оставить пиксель без изменений. Такой подход прост, но для z-буфера требуется множество памяти, а рендерер всё равно может потратить кучу тактов процессора на проецирование геометрии уровня, которую игрок не увидит.

В начале 1990-х у решения с z-буфером был ещё один недостаток: на IBM-совместимых PC, где использовалась система видеоадаптеров под названием VGA, запись в выходной буфер кадров была затратной операцией. Поэтому время, потраченное на отрисовку пикселей, которые потом просто будут перезаписаны, сильно снижало производительность рендерера.

Поскольку запись в буфер кадров была так затратна, идеальный рендерер должен был начинать с отрисовки ближайших к игроку объектов, затем объектов, находящихся непосредственно за ними, и так далее, пока не будет завершена запись в каждый пиксель экрана. На этом этапе рендерер должен был понимать, что пора остановиться, экономя таким образом всё время, которое он мог потратить на изучение далёких объектов, которые игрок не видит. Но упорядочивание объектов сцены таким образом, от ближайшего до самого дальнего, равносильно решению задачи VSD. Перед нами снова встаёт вопрос: что может видеть игрок?

Сначала Кармак пытался решить эту проблему, положившись на схему уровней Doom. Его рендерер начинал с отрисовки стен комнаты, в которой находится игрок, а затем выполнял заливку в соседние комнаты для отрисовки стен в этих комнатах, которые могли быть видны из текущей комнаты. Если каждая комната была выпуклой, это решало бы задачу VSD. Невыпуклые комнаты можно было разделить на выпуклые «секторы». Вы можете посмотреть, как эта техника рендеринга могла выглядеть в сильном замедлении в показанном выше видео, где пользователь YouTuber с ником Bisqwit демонстрирует собственный рендерер, работающий согласно тому же общему алгоритму. Этот алгоритм успешно использовался в игре Duke Nukem 3D, выпущенной через три года после Doom, когда процессоры стали мощнее. Но в 1993 году на доступном тогда оборудовании рендерер Doom, использующий этот алгоритм, испытывал проблемы со сложными уровнями. Особенно очевидно это было, когда секторы оказывались встроенными друг в друга, а это был единственный способ создания, например, круговых лестниц. Круговые лестницы требовали множества многократных рекурсивных спусков в уже отрисованный сектор, резко снижая скорость движка.

Примерно в то же время, когда команда id осознала, что движок Doom может оказаться слишком медленным, id Software попросили портировать Wolfenstein 3D на Super Nintendo. SNES была ещё менее мощной, чем IBM-совместимые PC того времени, и оказалось, что рендерер Wolfenstein с техникой ray-marching, несмотря на свою простоту, не выполнялся на оборудовании Super Nintendo с достаточной скоростью. Поэтому Кармак начал искать алгоритм получше. На самом деле именно для порта Wolfenstein на Super Nintendo Кармак впервые исследовал и реализовал двоичное разбиение пространства. В Wolfenstein оно было довольно простым, потому что все стены были параллельны осям; в Doom оно окажется сложнее. Но Кармак понял, что BSP-деревья решат проблемы со скоростью и в Doom.

Двоичное разбиение пространства

Двоичное разбиение пространства упрощает решение задачи VSD благодаря предварительному разделению 3D-сцены. Пока вам достаточно просто понять, чем полезно разделение сцены: если отрисовать линию (на самом деле являющуюся плоскостью в 3D) через всю сцену, зная при эом, с какой стороны от линии находится игрок или камера, то мы также будем знать, что ничто с другой стороны линии не сможет препятствовать объектам со стороны линии, где находится камера. Если повторить процесс много раз, то мы получим 3D-сцену, разделённую на множество секций. Это не будет улучшением по сравнению с исходной сценой, за исключением того, что теперь мы знаем больше о том, как различные части сцены могут перекрывать друг друга.

Первыми, кто написал о подобном разделении 3D-сцены, были исследователи, пытающиеся выяснить для ВВС США, достаточно ли прогрессивна компьютерная графика для использования в симуляторах полётов. Они опубликовали свои находки в отчёте 1969 года под названием «Исследование применения генерируемых компьютером изображений в визуальной симуляции». В отчёте был сделан вывод о том, что компьютерную графику можно использовать для обучения пилотов; одновременно исследователи предупреждали, что реализация системы будет осложнена задачей VSD:

Одна из самых значимых задач, которую нужно будет решать при вычислении изображений в реальном времени — это задача приоритета, или скрытых линий. В нашем повседневном визуальном восприятии окружающего мира эту задачу с тривиальной простотой решает сама природа; точка непрозрачного объекта перекрывает все остальные точки, лежащие вдоль той же линии видимости и находящиеся дальше. В случае компьютера эта задача очень сложна. Объём вычислений, необходимый для определения приоритета, в общем случае растёт экспоненциально с увеличением сложности окружений, и вскоре превосходят вычислительные нагрузки, связанные с поиском изображений объектов с учётом перспективы.

Одно решение, упомянутое этими исследователями, которое, по их словам, было ранее использовано в проекте НАСА, основано на создании того, что я буду называть «матрицей перекрытия». Исследователи указывают, что плоскость, делящая сцену на две части, может использоваться для разрешения «любого конфликта приоритетов» между объектами по разные стороны плоскости. В общем случае может потребоваться добавлять эти плоскости в сцену явным образом, но при определённом строении геометрии можно положиться на уже имеющиеся грани объектов. Исследователи демонстрируют показанный ниже пример, где p1, p2 и p3 — разделительные поверхности. Если точка обзора камеры находится на передней, или «истинной» стороне от одной из этих плоскостей, тогда pi равно 1. Матрица показывает взаимоотношения между тремя объектами в зависимости от трёх разделительных плоскостей и расположения точки обзора камеры — если объект ai перекрывает объект aj, тогда элемент aij матрицы будет равен 1.

Исследователи предложили реализовать эту матрицу аппаратно и заново вычислять её в каждом кадре. По-сути, матрица должна действовать, как большой переключатель или своего рода встроенный z-буфер. При отрисовке текущего объекта видео не выводится для частей объекта, когда в столбце объекта находится 1, а отрисовывается соответствующий объект строки.

Серьёзным недостатком такого подхода является то, что для описания сцены с n объектами нужна матрица размером n². Поэтому исследователи решили проверить, возможно ли представить матрицу перекрытия в виде «списка приоритетов», который будет иметь размер всего n и задавать порядок, в котором должны отрисовываться объекты. Они сразу же заметили, что в определённых сценах, например, в показанной выше, упорядочивание выполнить невозможно (так как существует цикл перекрытия), поэтому они очень много времени уделили математическому определению «правильных» и «неправильных» сцен. В конечном итоге они пришли к выводу, что по крайней мере для «правильных» сцен (а дизайнеру сцены достаточно легко избегать «неправильных» случаев), можно сгенерировать список приоритетов. Но генерацию списка они оставили как упражнение для читателя. Похоже, что основной вклад этой работы 1969 года заключается в том, чтобы указать, что по крайней мере теоретически должна существовать возможность использования разделительных плоскостей для упорядочивания объектов в сцене.

И только в статье 1980 года под названием «On Visible Surface Generation by A Priori Tree Structures» был продемонстрирован конкретный алгоритм для этого. В этой статье, написанной Генри Фуксом, Цви Кедемом и Брюсом Нейлором, было впервые описано BSP-дерево. Авторы говорят, что их новая структура данных является «решением, альтернативным подходу, впервые использованному десять лет назад, но из-за некоторых трудностей не так сильно распространнному», — так они отзываются от решении, выбранном в выполненной для ВВС США работе 1969 года. После построения BSP-дерева его можно легко использовать для упорядочивания с приоритетом объектов в сцене.

Фукс, Кедем и Нейлор представили достаточно понятное описание работы BSP-дерева, но я попробую дать менее формальное, зато краткое.

Мы начинаем с выбора одного полигона в сцене, и делаем плоскость, в которой лежит полигон, разделительной плоскостью. Этот один полигон также становится корневым узлом дерева. Оставшиеся полигоны сцены будут находиться с одной или другой стороны от корневой разделительной плоскости. Полигоны на «передней» стороне или в «переднем» полупространстве плоскости оказываются в левом поддереве корневого узла, а полигоны на «задней» стороне или в «заднем» полупространстве плоскости оказываются в правом поддереве. Затем мы рекурсивно повторяем этот процесс, выбирая полигоны из левого и правого поддеревьев в качестве новых разделительных поверхностей для их собственных полупространств, которые генерируют дальнейшие полупространства и поддеревья. Процесс завершается, когда заканчиваются полигоны.

Допустим, мы хотим рендерить геометрию сцены сзади вперёд. (Это называется «алгоритмом художника», потому что означает, что более далёкие от камеры полигоны будут закрашиваться полигонами, более близкими к камере, создавая правильный рендеринг.) Чтобы реализовать это, нам достаточно обойти по порядку наше BSP-дерево; решение о том, левое или правое поддерево должно отрисовываться, принимается на основании того, где находится точка обзора камеры — в переднем или заднем полупространстве относительно связанной с этим узлом разделительной плоскости. То есть в каждом узле дерева мы сначала рендерим все полигоны на «дальней» стороне плоскости, затем полигон на разделительной плоскости, а потом полигоны на «ближней» стороне плоскости. «Ближние» и «дальние» полигоны определяются относительно точки обзора камеры. Это решает задачу VSD, потому что, как мы узнали несколько абзацев назад, полигоны на дальней стороне разделительной плоскости не могут перекрывать ничего на передней стороне.

Показанная ниже схема демонстрирует построение и обход BSP-дерева, описывающего простую 2D-сцену. В 2D вместо разделительных плоскостей используются разделительные линии, но основная идея остаётся неизменной.

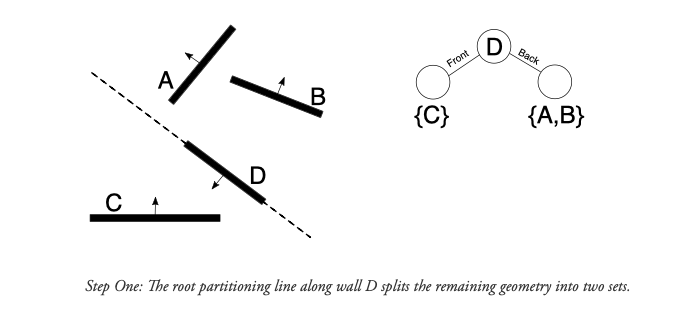
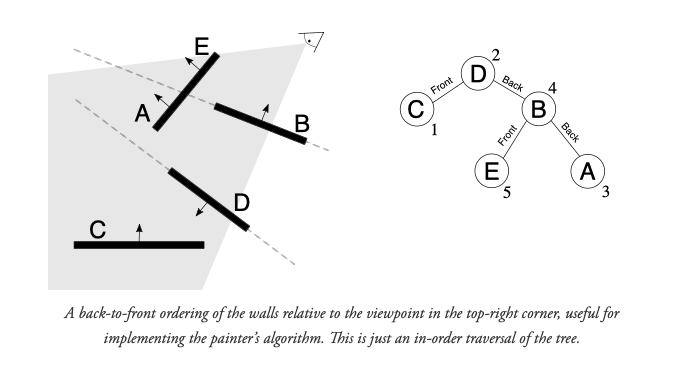
Очень удобное свойство BSP-дерева, которое Фукс, Кедем и Нейлор несколько раз подчёркивают — это то, что его нужно строить только один раз. Это кажется удивительным, но одно BSP-дерево можно использовать для рендеринга сцены вне зависимости от точки обзора камеры. BSP-дерево остаётся применимым, пока полигоны сцены не двигаются. Именно поэтому BSP-дерево так полезно для рендеринга в реальном времени — вся сложная работа по построению дерева может выполняться заранее, а не в момент рендеринга.

Фукс, Кедем и Нейлор сообщают, что дополнительного исследования требует вопрос создания «хорошего» BSP-дерева. Качество BSP-дерева зависит от того, какие полигоны вы выберете для задания разделительных плоскостей. Ранее я пропустил этот момент, но если при разбиении используется плоскость, пересекающая другие полигоны, то чтобы алгоритм BSP работал, вам нужно разделить пересечённые полигоны на два, чтобы одна половина относилась к одному полупространству, а другая — к другому. Если такое происходит часто, то построение BSP-дерева значительно увеличивает количество полигонов в сцене.

Брюс Нейлор, один из авторов статьи 1980 года, позже написал об этой проблеме в своей статье 1993 года «Constructing Good Partitioning Trees». По словам коллеги Кармака и сооснователя id Software Джона Ромеро, эта статья была одной из работ, которые читал Кармак, когда пытался реализовать BSP-деревья в Doom.

BSP-деревья в Doom

Вспомним, что в первом черновике рендерера Doom Кармак пытался установить порядок рендеринга для геометрии уровня, выполняя заливку рендерера наружу из комнаты, где находится игрок, в соседние комнаты. BSP-деревья были более удобным способом определения этого порядка, потому что они позволяли избежать проблемы многократного посещения рендерером одной комнаты (или сектора), впустую тратящей такты процессора.

Под «добавлением BSP-деревьев в Doom» на практике подразумевалось добавление генератора BSP-деревьев в редактор уровней Doom. После завершения создания уровня Doom из геометрии уровня генерировалось BSP-дерево. По словам Фабьена Санглара, процесс генерации мог занимать до восьми секунд для одного уровня и 11 минут для всех уровней первого Doom. Процесс генерации был таким длительным частично из-за того, что алгоритм генерации BSP Кармака пытается при помощи различных эвристик найти «хорошее» BSP-дерево. Задержка в восемь секунд была бы непростительной во время игры, но при предварительной генерации казалась вполне приемлемой, учитывая повышение производительности, которое обеспечивали BSP-деревья для рендерера. Сгенерированное BSP-дерево отдельного уровня сохранялось как часть данных уровня, загружаемых в игру при его запуске.

Кармак внёс важное изменение в алгоритм BSP-дерева, описанный в статье 1980 года: после запуска Doom и считывания BSP-дерева текущего уровня в память рендерер использует это дерево для отрисовки объектов не сзади вперёд, а спереди назад. В статье 1980 года Фукс, Кедем и Нейлор продемонстрировали, как BSP-дерево можно использовать для реализации алгоритма художника с отрисовкой сзади вперёд, но в алгоритме художника происходит большой объём повторной перерисовки, которая могла быть затратной на IBM-совместимых PC. Поэтому рендерер Doom начинает с более близкой к игроку геометрии, а затем отрисовывает дальнюю. Такой обратный порядок легко реализовать при помощи BSP-дерева, потому что можно просто принимать в каждом узле дерева решение обратного обхода. Чтобы более далёкая геометрия не отрисовывалась поверх более близкой, рендерер Doom использует своего рода неявный z-буфер, обеспечивающий многие из преимуществ обычного z-буфера, занимая при этом намного меньше памяти. Существует один массив, отслеживающий перекрытие в горизонтальном измерении, и два других массива, отслеживающих перекрытие в вертикальном направлении сверху и снизу экрана. Рендерер Doom мог обойтись без использования истинного z-буфера, потому что Doom, строго говоря, не был полностью трёхмерной игрой. Менее затратные структуры данных срабатывали в нём, потому что в Doom не были возможны определённые элементы: массив горизонтального перекрытия работал, потому что не было наклонных стен, а массивы вертикального перекрытия работали, потому что не было стен, в которых, например, есть два расположенных друг над другом окна.

Doom II, такой же сложный, как и его предшественник.

Но никто не жаловался на повторяемость кровищи.

Новое слово в технологиях Quake

Осталась единственная хитрая задачка — как встроить движущихся персонажей Doom в статическую геометрию уровней, отрисовываемых при помощи BSP-дерева. Враги в Doom не могли быть частью BSP-дерева, потому что они двигались; BSP-дерево работает только с неподвижной геометрией. Поэтому рендерер Doom сначала отрисовывает статическую геометрию уровня, отслеживая (при помощи ещё одной эффективно использующей память структуры данных) сегменты экрана, в которых была выполнена отрисовка. Затем он отрисовывает сзади вперёд врагов, усекая их по перекрывающим их сегментам экрана. Этот процесс не так оптимален, как рендеринг с помощью BSP-дерева, но поскольку обычно видно меньше врагов, чем геометрии, скорость здесь не становится проблемой.

Использование BSP-деревьев в Doom стало серьёзной победой. Очевидно, что Кармак оказался достаточно догадливым, чтобы понять, что идеальным решением задачи будут BSP-деревья. Но было ли это решение гениальным?

В своей превосходной книге о движке игры Doom Фабьен Санглар цитирует Джона Ромеро, сказавшего, что статья Брюса Нейлора «Constructing Good Partitioning Trees» в основном была посвящена использованию BSP-деревьев для отсечения задних граней 3D-моделей. По словам Ромеро, Кармак подумал, что алгоритм всё равно может оказаться полезным для Doom, поэтому он реализовал его. Это весьма похвально для Кармака, потому что подразумевает, что он увидел полезность BSP-деревьев в видеоиграх реального времени ещё тогда, когда остальные люди по-прежнему использовали эту технику для рендеринга статических сцен. Столь же лестная история есть в Masters of Doom: Кушнер предположил, что Кармак прочитал статью Нейлора и задался вопросом: «что если можно использовать BSP-дерево для создания не только одного 3D-изображения, но и целого виртуального мира?»

Эти выводы игнорируют историю BSP-дерева. Когда исследователи ВВС США впервые осознали, что разделение сцены может помочь в ускорении рендеринга, их интересовало ускорение рендеринга в реальном времени, потому что в конечном итоге они пытались создать авиасимулятор. Пример с авиасимулятором снова упоминается в статье 1980 года. Фукс, Кедем и Нейлор пишут о том, что BSP-дерево может быть полезным в симуляторе полётов, который пилоты используют для многократной отработки приземлений в одном и том же аэропорте. Так как геометрия аэропорта никогда не меняется, BSP-дерево можно сгенерировать только один раз. Очевидно, что они думали о симуляции в реальном времени. Во введении к статье они даже объясняют своё исследование проверкой возможности использования графической системы реального времени для создания изображений не более чем за 1/30 секунды.

То есть Кармак не первым задумался об использовании BSP-деревьев в графической симуляции реального времени. Разумеется, предвидеть, что BSP-деревья можно использовать таким образом, и реализовать это — совершенно разные вещи. Но даже при реализации у Кармака могло быть больше справочной информации, чем обычно считается. В статье Википедии о BSP-деревьях предполагается, что Кармак обращался к статье 1991 года Чена и Гордона, а также к учебнику 1990 года Computer Graphics: Principles and Practice. Хотя это утверждение не подтверждено цитатой, оно может быть правдой. В статье 1991 года Чена и Гордона описывается рендеринг спереди назад с использованием BSP-деревьев, что по сути является тем же решением, которое применялось в Doom, вплоть до структуры данных «неявный z-буфер», которая не позволяет отрисовывать дальние полигоны поверх ближних. В статье приведён отличный обзор BSP-деревьев, а также псевдокод для построения и отображения дерева. (Благодаря чудесной библиотеке моего университета мне удалось пролистать издание 1990 года.) Учебник Computer Graphics: Principles and Practice является классическим трудом по компьютерной графике, поэтому у Кармака он тоже мог быть.

Поделённый на подсекторы уровень E1M1: Hangar.

Как бы то ни было, Кармак столкнулся с новой задачей — «Как можно создать шутер от первого лица, работающий на компьютере с процессором, не способным даже выполнять операции с плавающей запятой?» — провёл собственные исследования, и доказал, что BSP-деревья — это полезная структура данных для видеоигр реального времени. Я всё равно считаю, что это впечатляющий результат, даже несмотря на то, что BSP-дерево было изобретено ещё десятью годами ранее, и достаточно подробно теоретически изучено ко времени, когда о нём прочитал Кармак. Возможно, главным достижением, которое мы должны славить, является движок Doom в целом, ставший великолепным примером кода. Я уже один раз говорил об этом, но повторюсь, что книга Фабьена Санглара о движке игры Doom (Game Engine Black Book: DOOM) — это превосходный обзор всех продуманных компонентов игрового движка и их взаимодействия. Мы не должны забывать, что задача VSD была только одной из множества задач, которые нужно было решить Кармаку для функционирования движка Doom. И что он смог, вдобавок ко всему, прочитать о сложной структуре данных, неизвестной большинству программистов, и реализовать её. Это многое говорит о об уровне его технических знаний и стремлении к идеалу.

Let's block ads! (Why?)