Парсер Хабра: Солнце, ветер и вода ver 0.2

суббота, 11 января 2020 г.

Солнце, ветер и вода ver 0.2

Геометрия парусов — измеряю «в живую»
высота топового угла грота $h_{гр топ}=11,2 м$ ;
высота галсового угла грота $h_{гр глс}=1,985 м$ ;
высота шкотового угла грота $h_{гр шкт}=2,179 м$ ;
расстояние шкотового угла грота от мачты $l_{гр шкт}=2,96 м$ ;
высота топового угла стакселя $h_{ст топ}=10 м$ ;
высота галсового угла стакселя $h_{ст глс}=1,111 м$ ;
высота шкотового угла стакселя $h_{ст шкт}=1,5 м$ ;
площадь грота $S_{гр}=17,2 м^2$ ;
площадь стакселя $S_{ст}=14 м^2$ ;
площадь боковой парусности корпуса $S_{anf}=7,315 м^2$ ;
площадь фронтальной парусности корпуса $S_{fr}=3 м^2$ ;
боковая проекция площади подводной части корпуса $S_{дп} w=1,82 м^2$ ;
площадь килей и скегов $S_{ks}=2,33 м^2$ ;
минимально возможный угол установки стакселя $\psi_{ст}=18^o$ .

Может это мне так не повезло, но ни один из производителей, во время моего поиска яхты, не согласился (не смог) предоставить эти данные для своей яхты. Я уверен, что у конструктора яхты вся эта информация есть, но получить ее почему то не получается. Буду добывать ее сам.
Буксировочную характеристику я уже получил с помощью оцифровки яхты в программе freeship, в награду за упорство программа сразу выдает и диаграмму остойчивости и точки центра тяжести и центра бокового сопротивления и много другой полезной геометрической информации. Диаграмма остойчивости показывает какой крутящий момент надо приложить к яхте, чтобы накренить ее на определенный угол.

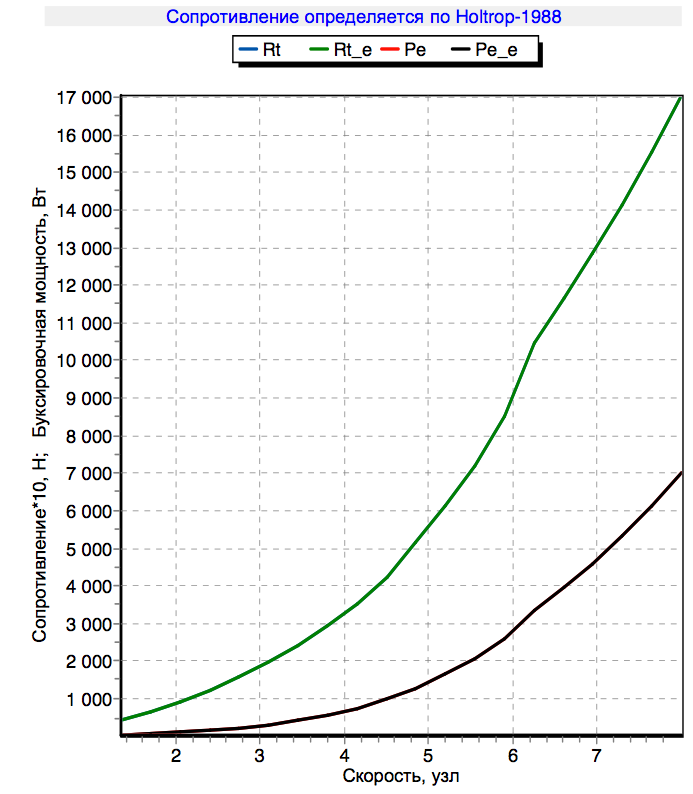
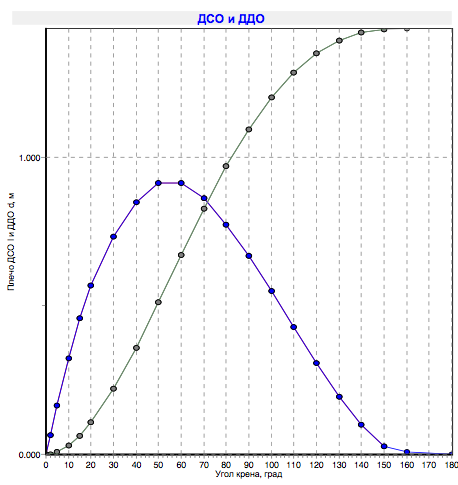
Все необходимые аргументы собраны, приступим к расчетам

Очевидно, что при движении вперед яхта преодолевает силу сопротивления встречного ветра. Скорость встречного ветра равна скорости движения яхты, но направлена противоположно. Я уже использовал эту аналогию, когда выбирал мотор.

$R_{fw}=0,61*S_{fr}*v^2, Н,$

где v — скорость судна.

В то же время на яхту действует сила реального ветра Frw, дующего под некоторым углом rw. Оба этих ветра создают силу равную векторной сумме частичных сил. Так называемую силу вымпельного ветра — ветра, дующего на борту судна.

Основная проблема заключается в теории относительности. Наблюдатель (и все измерительные приборы) находится на борту яхты и для него нет возможности измерить силу и направление реального ветра, зато он может измерить направление — $\alpha_{vw}$ и скорость вымпельного ветра — $v_{vw}$ , а также направление — $\alpha$ , измеренное бортовым компасом и скорость судна — $inline$ , измеренную бортовым лагом (спидометром).

Нахожу параметры реального ветра на основе измерений бортовых приборов.
$v_{rw}=\sqrt{v^2+v_{vw}^2-2*v*v_{vw}*cos(\alpha_{vw})}$ — скорость реального ветра;
$\alpha_{rw}=\pi-arccos(\frac{v_{rw}^2+v^2-v_{vw}^2}{2*v*v_{rw}})$ — угол реального ветра отложенный от направления «вперед».

Для маленьких покатушек все это не имеет смысла. Связь реального и вымпельного ветра необходима для планирования достаточно длительных путешествий (когда цель не находится в прямой видимости). Ведь планирование выполняется на на карте планеты с указанием реальных ветров (по прогнозу погоды), а движение яхты происходит от вымпельного ветра.

Теперь, когда связь с реальностью установлена, пора разобраться как возникает движущая сила. Понятно, что ветер наполняет паруса, и кораблик бежит по волнам.

На самом деле парус на яхте работает в двух основных режимах:

режим аэродинамического крыла — используется при встречных ветрах,
режим аэродинамического тормоза — используется при попутных ветрах.

Профиль паруса шьется таким образом, чтобы, будучи наполненным встречным ветром, принимать форму крыла. Т.е., есть крыло, движущееся с некоторой скоростью относительно воздуха — следовательно в нем возникает подъемная сила

$F_{air}$ . По аналогии с крылом самолета попробую упрощенно оценить ее величину и направление, относительно яхты.

Чтобы парус принял рабочую форму его необходимо немного повернуть относительно направления ветра. Угол поворота называется «угол атаки» $\alpha_{a}$ . Для простоты расчетов крыло сравнивают с плоской пластинкой, а различия представлены в виде таблицы аэродинамических коэффициентов, где Су — коэффициент отличия подъемной силы, а Сх — коэффициент отличия силы сопротивления. Подъемная сила направлена перпендикулярно пластинке, а сила сопротивления — параллельно. Геометрия пластинки задается коэффициентом аэродинамического удлинения $A_{y}=h^2/S$ , где h — высота паруса; S — площадь паруса.

Крыло, в отличии от пластинки, трехмерная конструкция, поэтому отдельная таблица показывает как влияет размер выпуклости «пуза» на коэффициенты отличия от пластинки.
Проекция силы паруса

$F_{air}$ на продольное направление яхты — полезная сила:

$F_{s}=0,61*v_{vw}^2*S*((Cy+Cy3)*sin(\alpha_{vw})-(Cx+Cx3)*cos(\alpha_{vw}))$ .
Проекция силы паруса

$F_{air}$ на поперечное направление яхты — сила дрейфа:

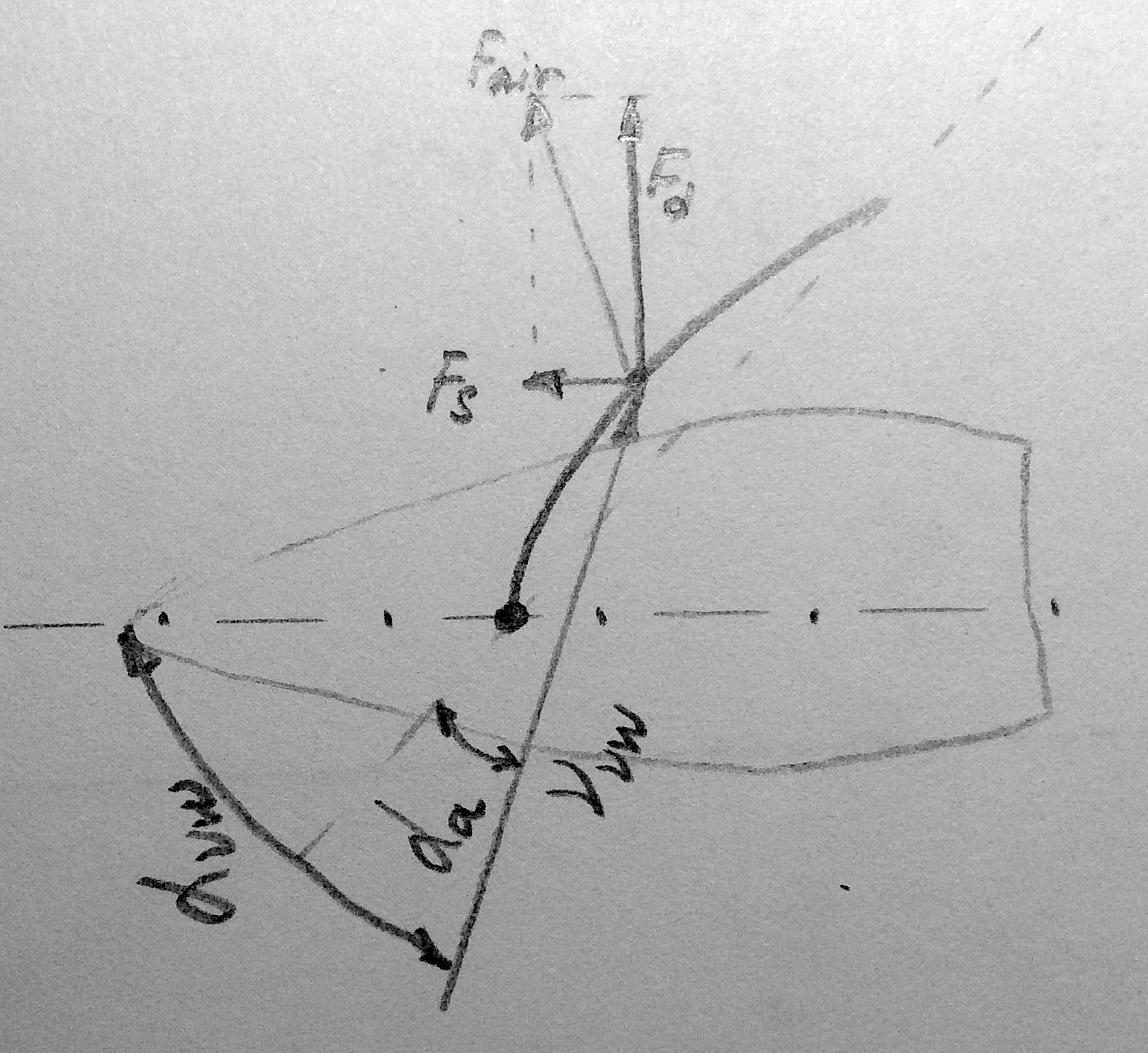
$F_{d}=0,61*v_{vw}^2*S*((Cy+Cy3)*cos(\alpha_{vw})-(Cx+Cx3)*sin(\alpha_{vw}))$ .

Сила ветрового сопротивления корпуса будет замедлять движение:

$R_{fw}=0,61*S_{fr}*v_{vw}^2*sin(\alpha_{vw})$
Получив проекции сил, могу найти вектора продольной и поперечной скорости яхты. Продольную составляющую скорости

$v_{дп}$ нахожу по графику буксировочной характеристики.
С поперечной составляющей все сложнее.
Для начала надо найти высоту центра парусности паруса. Парус представляет собой треугольник у которого одна сторона — выпуклая дуга. Представлю его как два паруса: треугольный и серпообразный кусок. Площадь треугольника вычисляется как половина произведения ширины на высоту, а площадь «серпа» это разность между площадью паруса и площадью треугольника.

$S=(h_{гр топ}-h_{гр глс})*l_{гр шкт}/2,$

где

$S_{серп}=S_{гр}-S$
Высота центра парусности паруса:

$h_{гр цп}=\frac{h_{гр \Delta цп}*S\Delta+((h_{гр топ}-h_{гр шкт})*S_{серп}/1,8)}{S_{гр}},$

где

$h_{гр \Delta цп}=h_{гр шкт}+(h_{гр топ}+h_{гр глс}-2*h_{гр шкт})/3 ,$ высота центра парусности треугольника паруса без серпа.
Обычно яхта имеет два паруса: основной — грот и передний — стаксель. Стаксель обычно выполняется без серпа и тогда его высота центра парусности:

$h_{ст \Delta цп}=h_{ст шкт}+(h_{ст топ}+h_{ст глс}-2*h_{ст шкт})/3$

Суммарный центр парусности:

$h_{\Sigma цп}=\frac{h_{гр цп}*S_{гр}+h_{ст \Delta цп}*S_{ст}}{S_{гр}+S_{ст}}$

Теперь могу определить кренящий момент, действующий на яхту:

$M_{кр}=F_{d}*h_{\Sigma цп}.$

По диаграмме остойчивости нахожу угол крена яхты

$\phi$ .
Выражаю силу сопротивления дрейфу яхты:

$R_{d}=9,8*102*(S_{ks}*atan(\frac{v_{d}}{v_{дп}})*v_{дп}^2*(cos(\phi-\gamma)-cos(\phi+\gamma))*0,96+(S_{ks}+S_{дп w})*1,15*v_{d}^2*cos(\phi-\gamma)),$

где — угол наклона килей двух-килевой яхты относительно вертикали.
Сила ветрового давления на корпус придает дополнительный дрейф.

$F_{anf}=0,61*v_{d}^2*S_{anf}*cos(\alpha_{vw}).$

Скорость

$v_{d}$ находится подстановкой по методу половинного деления до тех пор, пока не наступит баланс сил

$F_{d}+F_{anf}=R_{d}$ .
Теперь очевидно, что яхта движется " косо", т.е. имеет поперечную и продольную скорость перемещения. Это приносит еще один сюрприз. Направление —

$\alpha$ , измеренное бортовым компасом и скорость судна —

$v=v_{дп}$ , измеренное бортовым лагом (спидометром) показывают только продольную составляющую.
Надо привязать измерения к реальности. Реальный угол перемещения судна

$\alpha_{real}$ называется «путевой угол»:

$\alpha_{real}=atan(\frac{v_{d}}{v_{дп}})+\alpha$

и может отличаться от измеренного на 10-20 градусов.
Реальная скорость яхты может быть определена по теореме Пифагора:

$v_{real}=\sqrt{v_{дп}^2+v_{d}^2}.$

В завершении приведу пример расчета для моей яхты самой интересной ситуации — движение против ветра. Понятно, что строго против ветра под парусами не пойдешь, но под некоторым острым углом можно.

Начать надо с переднего паруса — стаксель закреплен сверху на мачте, передним углом к носу яхты, а задним с помощью шкота (мягкий трос) через ролик к лебедке. Его натяжение регулирует угол установки паруса относительно яхты. Минимальный угол установки $\psi_{ст мин}=18^o$ получается при максимальном натяжении шкота. Аэродинамическое удлинение стакселя $A_{y ст}=h_{ст}^2/S_{ст}=5,8$ . Методом линейной интерполяции нахожу оптимальный угол атаки $\alpha_{a}=10^o$ из таблицы аэродинамических коэффициентов. Критерий оптимальности — максимизация $F_{s ст}$ при этом Су=1,17; Сх=0,15. Установленный таким образом стаксель будет эффективно работать при направлении вымпельного ветра $\alpha_{vw}=\psi_{ст}+\alpha_{a}=18+10=28^o$ . Хорошая прогулочная яхтенная погода, когда скорость ветра в районе 5-7 м/с. Для красоты цифр возьму $v_{vw}=6,55 м/с$ .

Проекция силы стакселя на продольное направление яхты — полезная сила:

$F_{s ст}=0,61*6,55^2*14*((1,17+0)*sin(28*\pi/180)-(0,15+0)*cos(28*\pi/180))=153,5 H$

Проекция силы стакселя на поперечное направление яхты — сила дрейфа:

$F_{d ст}=0,61*6,55^2*14*((1,17+0)*cos(28*\pi/180)-(0,15+0)*sin(28*\pi/180))=405,8 H$

Ветровое сопротивление корпуса препятствует движению вперед.

$R_{fr w}=0,61*6,55^2*3*cos(28*\pi/180)=69 H$

По буксировочной характеристике определяем скорость

$v_{дп}=2,75$ узла=1,4 м/с

$h_{ст \Delta цп}=1,5+(10+1,5-2*1,1)/3=4,6 м$

$M_{кр ст}=405,8*4,6=1867 Н/м$ , по диаграмме остойчивости находим угол крена

$\phi_{ст}=3,9^o$ . Ну это мелочи, потому добавим еще один парус — грот!
Грот работает как закрылок у крыла самолета и вращается вокруг мачты на угол

$inline$ . Коэффициент аэродинамического удлинения грота

$A_{y гр}=h_{гр}^2/S_{гр}=4,9$ ;
оптимальный угол атаки

$\alpha_{a}=10^o$ ; Су=1,09; Сх=0,15.
Проекция силы грота на продольное направление яхты — полезная сила:

$F_{s гр}=0,61*6,55^2*17,2*((1,09+0)*sin(28*\pi/180)-(0,15+0)*cos(28*\pi/180))=170 H$

Проекция силы грота на поперечное направление яхты — сила дрейфа:

$F_{d гр}=0,61*6,55^2*17,2*((1,09+0)*cos(28*\pi/180)-(0,15+0)*sin(28*\pi/180)))=464 H$

$h_{\Sigma цп}=4,16 м$ ,

$M_{кр}=3127 H$ , а угол крена

$\phi_{\Sigma}=8,5^o$ .
Суммарная сила движения вперед:

$F_{s} =F_{s ст}+F_{s гр}-R_{fr w}=153,5+170-69=254 H$ , скорость движения вперед

$v_{дп}=3,6$ узла или 1,86 м/с.
Если предположить, что реальный ветер дует строго северный, то компас на борту будет показывать угол продольной составляющей скорости яхты

$\alpha_{vw}=38,1^o$ .
Скорость дрейфа составит

$v_{d}=0,418 м/с$ .
Теперь надо привести эти результаты к реальности.

Путевой угол реального движения составит:
$\alpha_{real}=atan(\frac{v_{d}}{v_{дп}})+\alpha=atan(\frac{0,418}{1,86})+38,1=51^o$ , это и есть угол реального ветра $\alpha_{rw}$ к вектору движения яхты.

А реальная скорость перемещения в пространстве: $v_{real}=\sqrt{v_{дп}^2+v_{d}^2}$ =1,92+0,4182=1,9 м/с.
Скорость реального ветра:
$v_{rw}=\sqrt{v^2+v_{vw}^2-2*v*v_{vw}*cos(\alpha_{vw})}= 5 м/с$ .
При таких условиях скорость продвижения строго против ветра составит 1,2 м/с или 2,35 узла, а двигаться придется по зигзагообразной траектории — галсами.

Проведя расчет для других возможных углов вымпельного ветра можно получить круговую лавировочную диаграмму зависимости реальной скорости яхты от реального ветра. 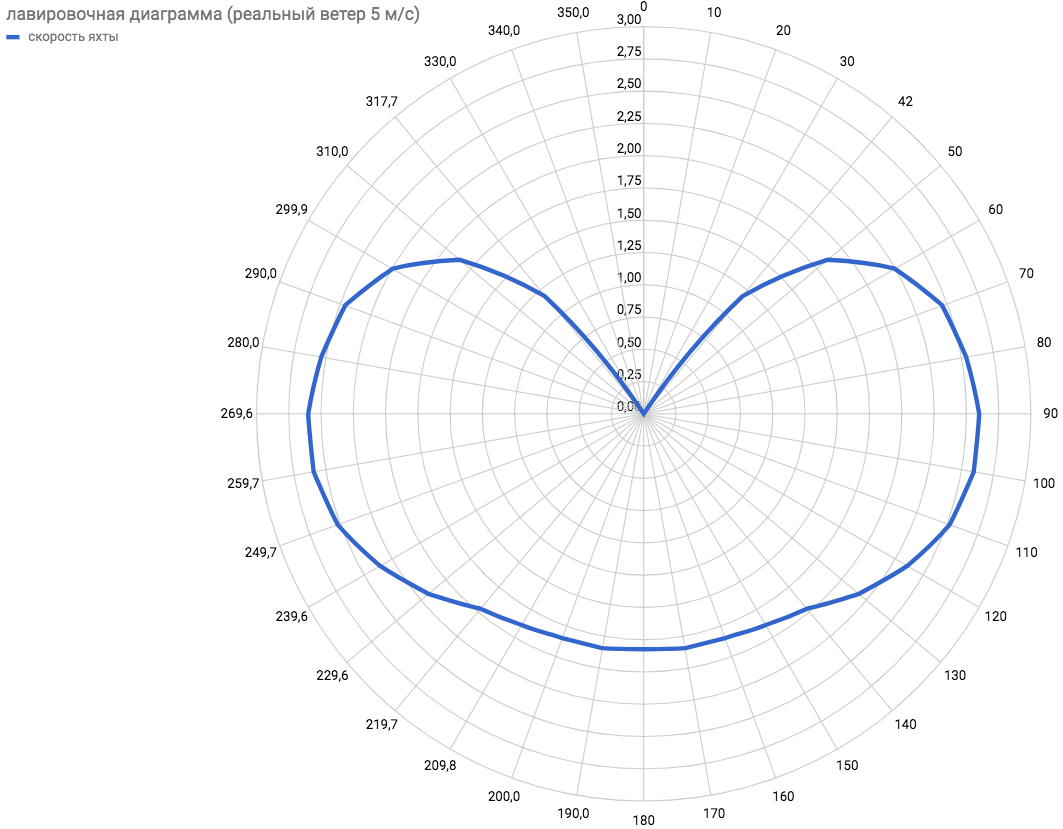С помощью ее уже можно планировать маршруты на карте по прогнозу ветров. Дополнительно стало понятно, что минимально возможный угол $\alpha_{real min}=43,5^o$ , а максимальная скорость движения против ветра достигается с курсовым углом $50^o<\alpha_{real}<53^o$ для ветра 5 м/с.