
Помню, как однажды увидел фотографию выше на Flickr и сломал мозг, пытаясь понять, что с ней не так. Дело было в том, что пропеллер вращался в то время, когда датчик движения в камере «считывал показания», то есть во время экспозиции камеры происходило какое-то движение. Об этом действительно стоит подумать, давайте-ка подумаем вместе.
Многие современные цифровые камеры используют КМОП-матрицу в качестве своего «чувствительного» устройства, также известную как активный датчик пикселей, который работает путем накопления электронного заряда при падении на него света. По истечении определенного времени – времени экспозиции – заряд построчно перемещается обратно в камеру для дальнейшей обработки. После этого камера сканирует изображение, построчно сохраняя ряды пикселей. Изображение будет искажено, если во время съемки присутствовало хоть какое-то движение. Для иллюстрации представьте съемку вращающегося пропеллера. В анимациях ниже красная линия соответствует текущему положению считывания, и пропеллер продолжает вращаться по мере считывания. Часть под красной линией – это полученное изображение.
Первый пропеллер совершает 1/10 часть вращения во время экспозиции:

Подписывайтесь на каналы:
@Ontol — самые интересные тексты/видео всех времен и народов, влияющие на картину мира
@META LEARNING — где я делюсь своими самыми полезными находками про образование и роль ИТ/игр в образовании (а так же мыслями на эту тему Антона Макаренко, Сеймура Пейперта, Пола Грэма, Джозефа Ликлайдера, Алана Кея)
Изображение немного исказилось, но ничего критичного. Теперь пропеллер будет двигаться в 10 раз быстрее, совершая полное вращение за время экспозиции:

Это уже похоже на ту картинку, что мы видели в начале. Пять раз за экспозицию:

Это уже немного чересчур, так можно и с катушек съехать. Давайте повеселимся и проверим как будут выглядеть различные объекты при различных скоростях вращения за экспозицию.
Точно такой же пропеллер:

Пропеллер с большими лопастями:

Колесо автомобиля:

Мы можем воспринимать эффект роллинг-шаттера как некое преобразование координат реального объекта из «объектного пространства» в «пространство изображения» искаженного объекта. Анимация ниже показывает, что происходит с Декартовой системой координат при увеличении числа оборотов. При малых оборотах деформация незначительна – число увеличивается до единицы, и каждая сторона системы координат последовательно перемещается в правую сторону изображения. Это довольно сложная трансформация для восприятия, но легкая в понимании.

Пусть изображение будет I(r,θ), реальный (вращающийся) объект будет f(r,θ), где (r,θ) — это 2D полярные координаты. Мы выбрали полярные координаты для этой задачи из-за вращательного движения объектов.
Объект вращается с угловой частотой ω, а шаттер перемещается по изображению со скоростью v по вертикали. В положении (r,θ) на картинке, дистанция, которую прошел шаттер с начала экспозиции, равна y=rsinθ, где прошедшее с этого момента время равно (rsinθ)/v. За это время объект повернулся на (ω/v)rsinθ) радианов. Итак, мы получаем
I(r,θ)=f(r,θ+(ω/v)rsinθ),
что и является требуемой трансформацией. Коэффициент ω/v пропорционален числу вращений за экспозицию и параметризует трансформацию.
Чтобы получить более глубокое представление об очевидных формах пропеллеров, мы можем рассмотреть объект, состоящий из P пропеллеров, где f является ненулевым только для
θ=2π/P,4π/P…2π=2pπ/P для 1<p<P.
Изображение I является ненулевым для θ+(ω/v)rsinθ=2pπ/P или
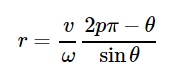
В Декартовой системе координат оно становится
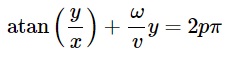
и помогает нам в объяснении причины, по которой пропеллеры принимают S-образную форму – это просто функция арктангенса в пространстве изображения. Круто. Ниже я построил эту функцию с набором пяти лопастей пропеллера с несколько различными начальными сдвигами, вы можете увидеть это на воспроизведении. Они очень похожи на фигуры из анимаций выше.
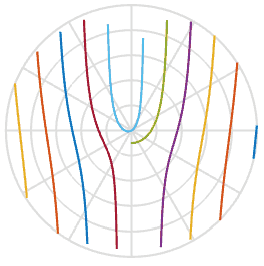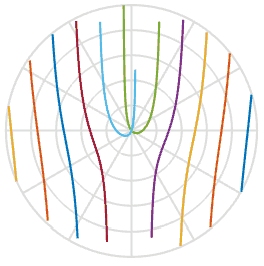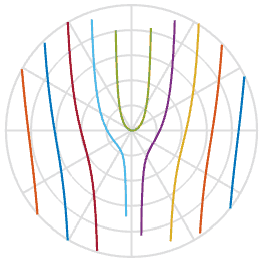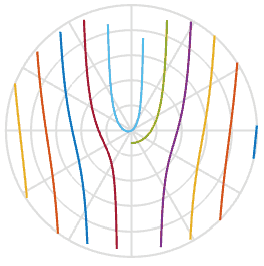
Раз мы узнали немного больше о процессе, можем ли мы исправить испорченные фотографии? Используя одно из изображений выше, я могу провести через него линию, повернуть назад и вставить эти пиксели в новое изображение. В анимации ниже я сканирую изображение слева, помеченное красной линией, а затем вращаю пиксели вдоль этой линии, получая новое изображение. Так мы можем воссоздать изображение реального объекта, даже если вдруг назойливый роллинг-шаттер испортил вам фотографию.

Эх, если бы я лучше владел фотошопом, я бы извлек пропеллеры из первоначальной фотографии на Flickr, отредактировал бы и вернул на фотографию. Кажется, я знаю, чем займусь в будущем.
Если вы хотите узнать реальное количество лопастей на фотографии в начале поста и скорость вращения, можете прочитать этот отличный пост на Tumblr Дэниела Уолша, в котором он дает математическое объяснение.
Он считает, что мы можем подсчитать количество лопастей, вычитая «нижние» лопасти из «верхних», так мы получаем три лопасти на той картинке. Также мы знаем, что пропеллер прокручивается примерно дважды за время экспозиции, поэтому, если мы попытаемся «отменить» вращение с несколькими различными скоростями, то получим примерно это:

Я должен был понять, где находится центр пропеллера, поэтому нарисовал круг. Судя по всему, центр должен быть где-то рядом. К сожалению, одна лопасть отсутствует, но для изображения информации хватает.
Я нашел местечко, где все пересекается больше всего, поэтому, при этой скорости вращения (2.39 оборота за экспозицию), вот как выглядит исходное изображение и лопасти:

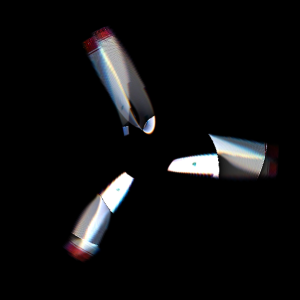
К сожалению, картинка не идеальна, но по крайней мере очень приближена к реальности.
Об авторе: Джейсон Коул – аспирант из Лондона, который горит математикой, физикой и визуализацией данных. Здесь его вебсайт. А статья была опубликована здесь.
Подписывайтесь на каналы:
@Ontol — самые интересные тексты/видео всех времен и народов, влияющие на картину мира
@META ОБУЧЕНИЕ, где я делюсь своими самыми полезными находками про образование и роль ИТ/игр в образовании (а так же мыслями на эту тему Антона Макаренко, Сеймура Пейперта, Пола Грэма, Джозефа Ликлайдера, Алана Кея)

Узнайте подробности, как получить востребованную профессию с нуля или Level Up по навыкам и зарплате, пройдя платные онлайн-курсы SkillFactory:
Комментариев нет:
Отправить комментарий