MCMC-методы и коронавирус: часть первая, вступительная

Привет, коллеги! Сто лет не писал на Хабр, но вот время настало. Весной этого года я вёл курс «Advanced ML» в Академии больших данных Mail.ru; кажется, слушателям понравилось, и вот сейчас меня попросили написать не столько рекламный, сколько образовательный пост об одной из тем моего курса. Выбор был близок к очевидному: в качестве примера сложной вероятностной модели мы обсуждали крайне актуальную (казалось бы… но об этом позже) в наше время эпидемиологическую SIR-модель, которая моделирует распространение болезней в популяции. В ней есть всё: и приближённый вывод через марковские методы Монте-Карло, и скрытые марковские модели со стохастическим алгоритмом Витерби, и даже presence-only data.

С этой темой вышло только одно небольшое затруднение: я начал было писать о том, что я собственно рассказывал и показывал на лекции… и как-то быстро и незаметно набралось страниц двадцать текста (ну ладно, с картинками и кодом), который всё ещё не был закончен и совершенно не был self-contained. А если рассказывать всё так, чтобы было понятно с «нуля» (не с абсолютного нуля, конечно), то можно было бы и сотню страниц написать. Так что когда-нибудь я их обязательно напишу, а сейчас пока представляю вашему вниманию первую часть описания SIR-модели, в которой мы сможем только поставить задачу и описать модель с её порождающей стороны — а если у уважаемой публики будет интерес, то можно будет и продолжить.

I love my friends and they love me,
We're just as close as we can be.
And just because we really care,
Whatever we get, we share!

Tom Lehrer. I Got It From Agnes

Итак, давайте разбираться. Неформально основные предположения SIR-модели выглядят так:

• есть некоторая популяция людей, в которой может гулять некий страшный вирус;
• изначально вирус в популяцию так или иначе попадает (например, появляется первый заболевший), а затем люди заражаются друг от друга;
• название SIR происходит от трёх состояний, в которых может находиться человек в этой модели:
     ○ Susceptible (ещё не заболел, но подвержен болезни, т.е. может заразиться),
     ○ Infected (заболел и заражает других) и
     ○ Recovered (выздоровел).

Для простоты будем предполагать, что у переболевших всегда вырабатывается иммунитет, и они исключаются из круговорота вируса в природе. Соответственно, переходы между этими состояниями могут быть только слева направо: Susceptible → Infected → Recovered.

Задача состоит в том, чтобы, собственно, обучить эту модель, то есть понять что-то о параметрах процесса заражения по данным. Как выглядят данные, понять легко, — это просто число зарегистрированных заражённых в каждый момент времени, которых мы будем обозначать вектором $$. Например, когда я давал домашнее задание в курсе про коронавирус (оно было, впрочем, о других моделях), данные по России выглядели так:

[2,2,2,2,3,4,6,8,10,10,10,10,15,20,25,30,45,59,63,93,114,147,199,253,306,438,438,495,658,840,1036,1264,1534,1836,2337,2777,3548,4149,4731,5389,6343,7497,8672]

А вот что за параметры у этой модели, как они сопрягаются друг с другом и как их обучать, тем более по такому крохотному датасету, — это вопрос более серьёзный.

В целом я буду следовать общей канве работы (Fintzi et al., 2016), в которой строятся MCMC-алгоритмы для моделей SIR, SEIR и некоторых их вариантов. Но по сравнению с (Fintzi et al., 2016) я буду сильно упрощать и модель, и её изложение. Главное упрощение состоит в том, что вместо непрерывного времени, которое рассматривается в исходной работе, мы будем рассматривать дискретное время, то есть вместо непрерывного процесса, который в какой-то момент порождает события вида «заразился» и «выздоровел», мы будем считать, что люди проходят набор дискретных точек времени $$. Это упрощение позволит нам, во-первых, избавиться от множества технических сложностей, а во-вторых, перейти от алгоритма Метрополиса-Гастингса в общем виде к алгоритму сэмплирования по Гиббсу, то есть не высчитывать отношение Метрополиса, как это приходится делать в (Fintzi et al., 2016). Если вы не поняли, что это я такое сейчас сказал, не беспокойтесь: сегодня этого нам не понадобится, а если будут следующие части, я там всё объясню.

Мы будем обозначать состояния SIR-модели через S, I и R соответственно, а состояние человека $$ в момент времени $$ — через $$. Заодно сразу заведём переменные для общего числа ещё не заболевших $$, больных $$ и выздоровевших $$ в момент времени $$. Всего человек у нас будет $$, так что для любого $$ будет выполняться $$. И, как я уже писал выше, $$ из них — это зарегистрированные (протестированные) заболевшие люди.

Неизвестные параметры модели — это $$, где:

• $$ — начальное распределение заболевших; иначе говоря, $$ для каждого $$; в нашей упрощённой модели мы не будем обучать $$, а просто будем фиксировать 1-2 заболевших в первый момент времени;
• $$ — вероятность обнаружить инфицированного в общей популяции, то есть вероятность того, что человек $$ в момент $$, когда $$, будет обнаружен тестированием и зачислен в данные $$; иначе говоря, для каждого заболевшего человека мы подбрасываем монетку, определяя, найдёт его тестирование или нет, так что текущий элемент данных $$ имеет биномиальное распределение с параметрами $$ и $$:

  $$

• $$ — вероятность для заболевшего выздороветь за один шаг времени, то есть вероятность перехода из состояния $$ в состояние $$;

А $$ — это самый интересный параметр, показывающий вероятность заразиться за один отсчёт времени от одного инфицированного человека. Это значит, что в модели мы предполагаем, что все люди в популяции «общаются» друг с другом (под «общением» здесь понимается контакт, достаточный для передачи заболевания; коронавирус передаётся в основном воздушно-капельным путём, но, конечно, моделировать можно и распространение любого другого заболевания; см., например, эпиграф), и вероятность заразиться зависит от того, сколько сейчас заражённых, то есть от того, чему равно $$. Мы будем предполагать самую простую модель, в которой вероятность заразиться от одного инфицированного равна $$, и все эти события независимы, а значит, вероятность остаться здоровым равна

$$

В этих предположениях на самом деле есть что обсудить. Самое удивительное здесь, на мой личный взгляд, — биномиальное распределение для $$. Подбрасывать монетку с вероятностью обнаружить заражённого — это абсолютно нормально, но не очень реалистично выглядит то, что эту монетку мы бросаем заново на каждом шаге, то есть мы можем «забыть» уже обнаруженного заражённого человека. В результате из SIR-модели может получаться (и часто получается) совсем не монотонная последовательность $$; это странно, но большого влияния на результат, похоже, не оказывает, а моделировать этот процесс более реалистично было бы гораздо сложнее.

Кроме того, очевидно, что эта модель предназначена для замкнутой популяции, где каждый «общается» с каждым, так что запускать её, скажем, для России с параметром N в сто миллионов или для Москвы с параметром десять миллионов никакого смысла не имеет (да и вычислительно не получится). Важное направление расширений и продолжений SIR-моделей именно этому и посвящено: как добавить сюда более реалистичный граф взаимодействий и возможных заражений; об этом мы, наверное, поговорим уже в последнем, заключительном посте.

Но при всех этих упрощениях теперь при помощи вышеприведённых параметров мы можем выписать матрицу вероятностей перехода между состояниями. Эти вероятности (точнее, конкретно вероятность заразиться) зависят от общей статистики популяции. Давайте обозначим вектор состояний всех людей, кроме $$, через $$, и распространим то же обозначение на все остальные переменные; например, $$ — это число заражённых в момент времени $$, не считая $$. Тогда для вероятностей перехода из $$ в $$ мы получаем

$$

$$

$$

$$

а во всех остальных случаях

$$

То же самое можно нагляднее записать в виде матрицы вероятностей переходов (порядок строк и столбцов естественный, S-I-R):

$$

Читателю, знакомому с марковскими цепями и марковскими моделями, может показаться, что это всего лишь скрытая марковская модель: есть скрытые состояние, есть понятное распределение наблюдаемых для каждого скрытого состояния, переходы действительно марковские, то есть следующее скрытое состояние зависит только от предыдущего… Но есть, как говорится, один нюанс: вероятности перехода нельзя считать постоянными, они меняются вместе с изменением $$, и это крайне существенный аспект модели, который никак нельзя выбросить.

Поэтому вывод в этой модели внезапно становится гораздо сложнее, чем в обычной скрытой марковской модели (хотя там тоже не всегда такой уж подарок). Однако, хотя вывод и сложнее, он всё-таки подвластен человеческому разуму — в следующих инсталляциях (если они будут) я об этом как раз и расскажу. А на сегодня почти уже хватит — давайте теперь немножко расслабимся и попробуем поиграться с этой моделью пока что в порождающем смысле.

Как большой ценитель и эксперт
в карантин садился интроверт.
***
«Работать дома я бы не смогла», —
пыталась объяснить глистам пчела.
***
Каганов умер, весело шутя.
Конечно, очень жаль его, хотя…

Леонид Каганов. Карантинки

Если параметры модели известны, и нужно просто породить траекторию того, как могло бы развиваться распространение болезни в популяции, в SIR ничего сложного нет. Код ниже порождает пример популяции согласно нашей модели; состояния я закодировал как $$, $$, $$. Как и предупреждал, для простоты буду считать, что в момент времени $$ в популяции ровно один заболевший, а дальше уже как пойдёт.

def sample_population(N, T, true_rho, true_beta, true_mu):
    true_log1mbeta = np.log(1 - true_beta)

    cur_states = np.zeros(N)
    cur_states[:1] = 1
    cur_I, test_y, true_statistics = 1, [1], [[N-1, 1, 0]]

    for t in range(T):
        logprob_stay_healthy = cur_I * true_log1mbeta
        for i in range(N):
            if cur_states[i] == 0 and np.random.rand() < -np.expm1(logprob_stay_healthy):
                cur_states[i] = 1
            elif cur_states[i] == 1 and np.random.rand() < true_mu:
                cur_states[i] = 2

        cur_I = np.sum(cur_states == 1)
        test_y.append( np.random.binomial( cur_I, true_rho ) )
        true_statistics.append([np.sum(cur_states == 0), np.sum(cur_states == 1), np.sum(cur_states == 2)])

    return test_y, np.array(true_statistics).T

N, T, true_rho, true_beta, true_mu = 100, 20, 0.1, 0.05, 0.1
test_y, true_statistics = sample_population(N, T, true_rho, true_beta, true_mu)

Этот код выдаёт не только собственно данные $$, но и «истинные» статистики $$, $$, $$, чтобы их можно было визуализировать. Давайте это и сделаем; для параметров $$, $$, $$, $$, $$ может получиться примерно такая картинка:

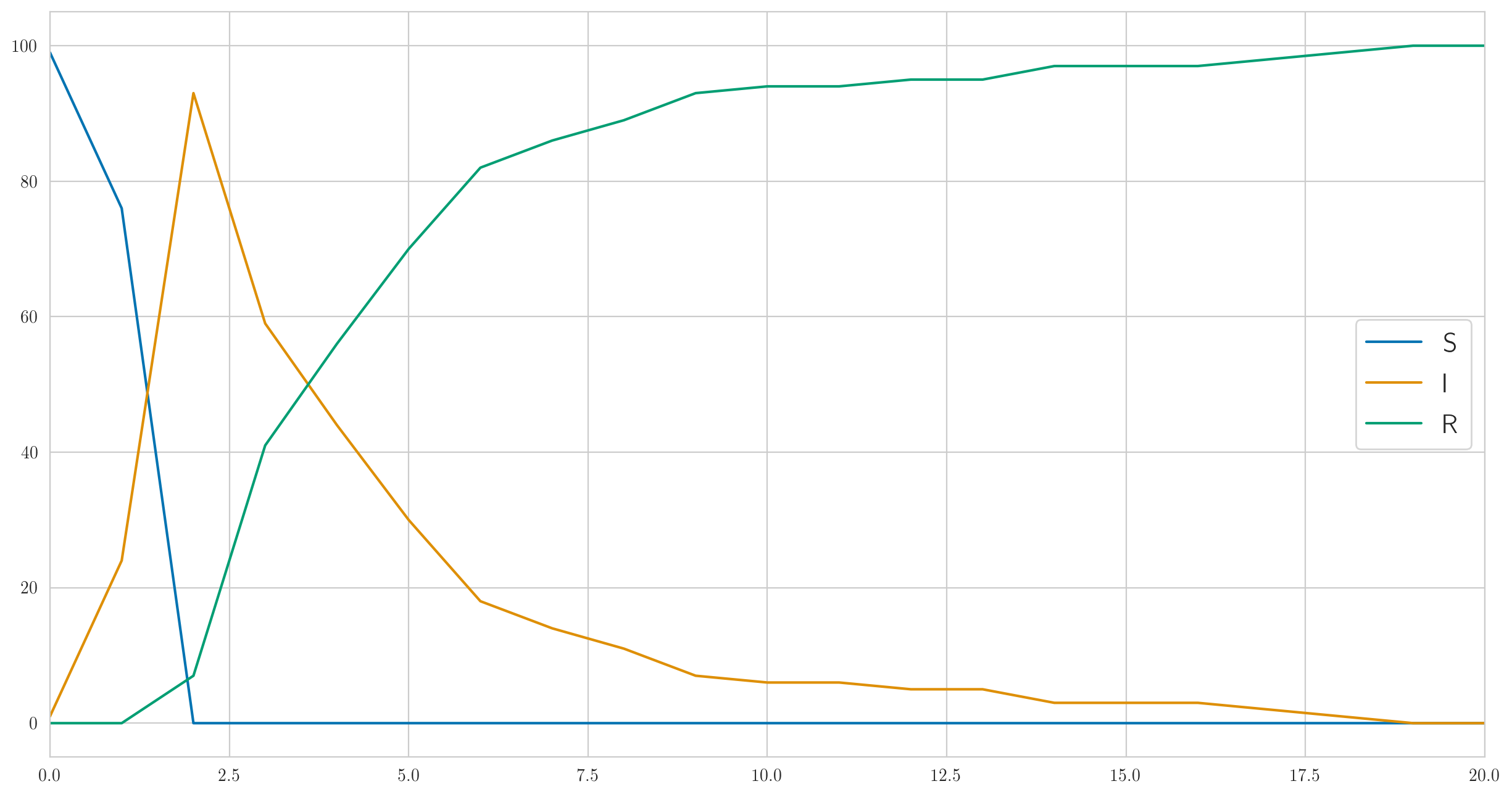
Как видите, в этом примере все заболевают очень быстро, а потом потихоньку начинают поправляться. А собственно наблюдаемые данные о заболевших выглядят так:

[ 1  6  13  6  6  4  1  0  0  1  0  1  2  0  0  0  0  0  1  0  0]

Обратите внимание, что, как мы обсуждали выше, монотонности здесь никакой нет.

Но это, конечно, не единственное возможное поведение. Параметры я выше выбрал так, чтобы заражение было достаточно быстрым и болезнь почти сразу охватывала все сто человек в нашей тестовой популяции. А если сделать $$ поменьше, например $$, то заражение пойдёт уже гораздо медленнее, и даже не все успеют переболеть до того, как поправится последний заболевший и не останется. Примерно так:

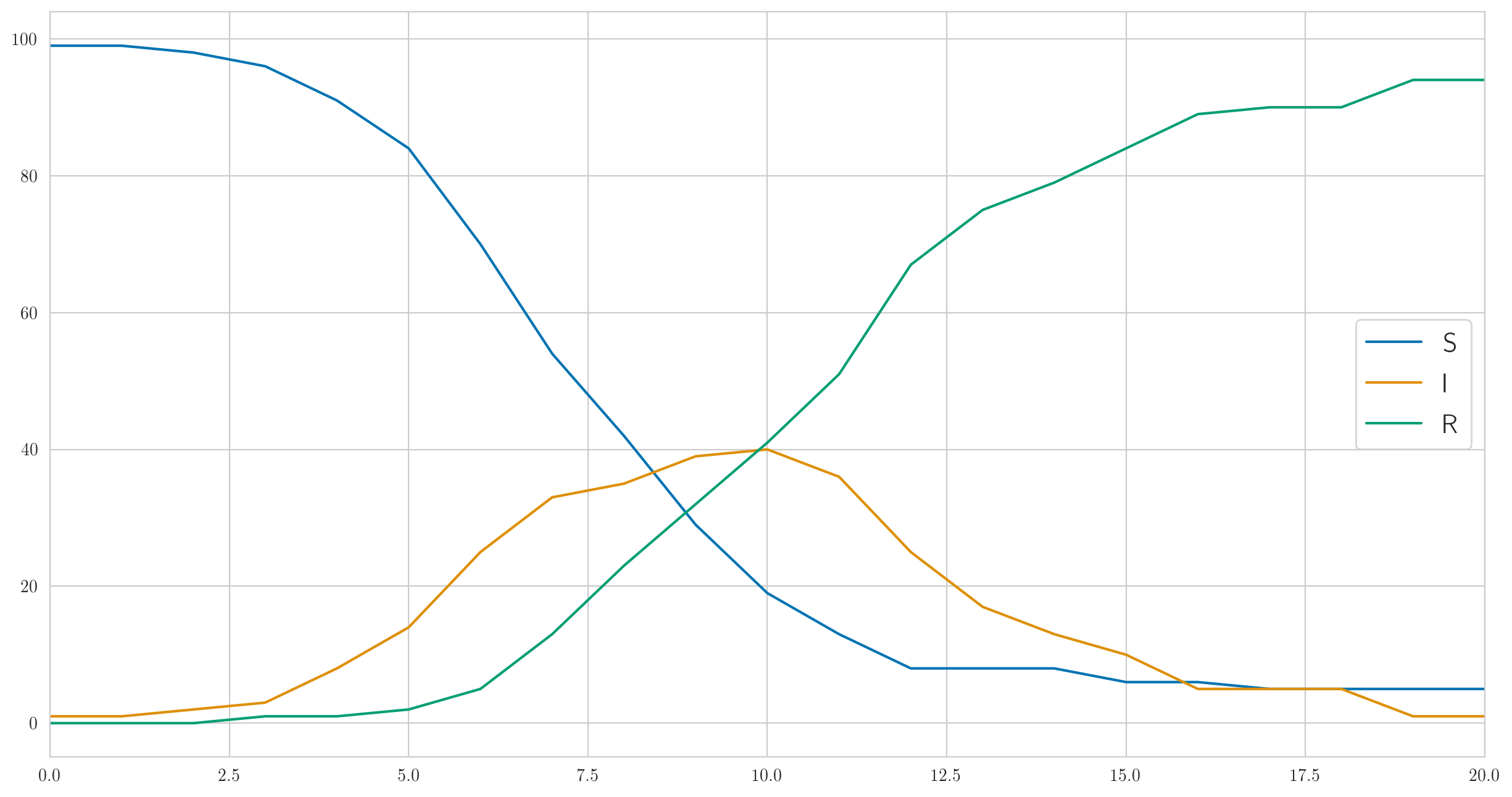
И число выявленных случаев тоже уже совсем другое:

[1  0  0  0  0  1  2  2  3  1  1  9  3  1  3  1  0  1  0  0  0]

Можно и ещё сильнее «задушить» болезнь; например, давайте оставим $$, но выставим $$, то есть на каждом временном отрезке у каждого заболевшего есть шанс поправиться в 0.5 (в конце концов, это логично: или поправится, или нет). Тогда переболеют страшным вирусом уже только 50-60 человек из 100; кривые могут выглядеть, например, так:

[1  0  0  1  3  2  1  1  0  3  0  0  0  0  0  1  0  0  0  0  0]

Но общая картина, конечно, в любом случае выглядит примерно одинаково: сначала экспоненциальный рост, а затем выход на насыщение; разница только в том, успеет ли выздороветь последний носитель раньше, чем все перезаражаются.

Ну что ж, пора подводить промежуточные итоги. Сегодня мы увидели, как выглядит одна из самых простых эпидемиологических моделей. Несмотря на кучу упрощающих предположений, SIR-модель даже в таком изложении всё равно очень полезна; дело в том, что большинство её расширений достаточно прямолинейны и общую суть дела не меняют. Поэтому, если будем продолжать, в следующей серии я расскажу о том, как обучать модель SIR; впрочем, это повлечёт за собой столько интересного, что наверняка в один пост тоже не поместится. До новых встреч!

Let's block ads! (Why?)