«Если вам кажется, что вы понимаете квантовую теорию… то вы не понимаете квантовую теорию.» — Фейнман Р., лекции «Характер физических законов» (1964), гл. 6.
Это и подобные высказывания о непостижимости законов квантовой механики всегда раздражали меня. Корпускулярно-волновой дуализм, свойства квантовых частиц вести себя как волны и как частицы — неужели нельзя их понять наглядно, увидеть не как поведение математических решений, а воочию? В этом обзоре я представлю результаты, оспаривающие этот мистицизм.
Вывод соотношения де Бройля
Луи де Бройлю были известны соотношения (формула Планка) и (эквивалентность массы и энергии в специальной теории относительности) где – масса покоя, т.е. масса в собственной системе отсчёта.
Согласно теории относительности абсолютного времени нет, и у каждой точки пространства оно своё собственное – четвертая координата t. Собственное время, как рассуждал Луи де Бройль, это как личные часы. Они есть как у человека, так и у электрона. Что это значит?
Он предположил, что каждой частице свойственен внутренний периодический процесс (тик-так с частотой ), который служит мерой собственного времени [1]. Этот самый внутренний процесс с частотой в собственной системе отсчета позволяет связать две формулы энергии
Неподвижный наблюдатель воспринимает колебательный процесс частицы летящей со скоростью в точке как
Переход в систему отсчёта частицы даёт в показателе экспоненты
то есть бегущую волну – волну де Бройля, которая всегда синхронизирована по фазе с внутренним процессом
Подставляя формулы для энергии, получаем
В таком случае частице, летящей со скоростью соответствует длина волны
где – импульс частицы, а – постоянная Планка.
Это была математика. Теперь найдем реальный объект, для которого собственные колебания синхронизированы с волной.
Частицы-волны? Силиконовые капли-волны!
Французский физик Ив Куде исследовал поведение прыгающей капли-«блинчика» силиконового масла на поверхности жидкости в вибрационной ванне. Слой жидкости (силиконового масла) в ванне был толщиной 4 мм. Под действием вибрации на поверхности появляется рябь (волны Фарадея), если вертикальное ускорение при вибрировании больше пороговой величины (4.5g в условиях эксперимента). Однако, в подпороговом режиме вибрации с частотой 50 Гц в ванне 40x40 мм дают иную картину стоячих волн с длиной =6.5 мм. Капля силиконового масла размером 1 мм, аккуратно помещенная на поверхность, прыгает по этим волнам не собираясь останавливаться.
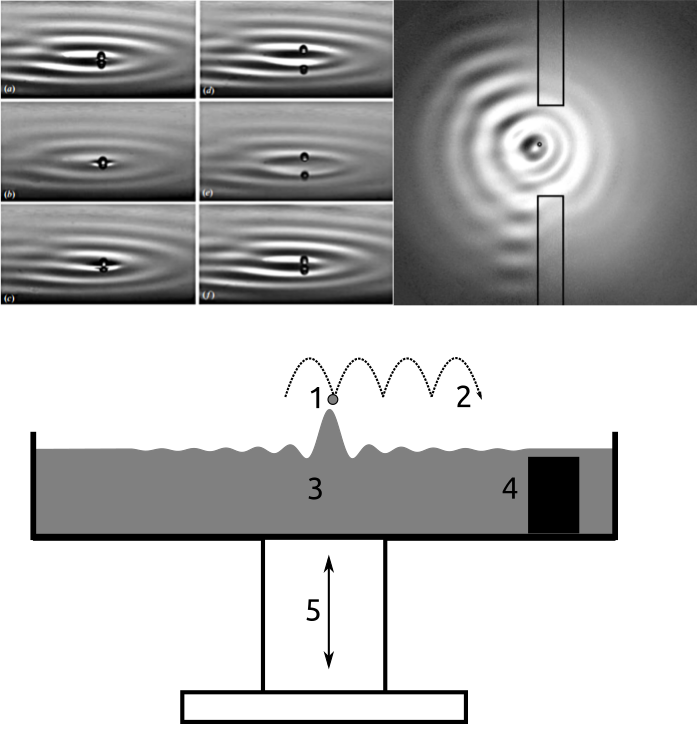
Экспериментальная установка Ива Куде. Левая верхняя часть рисунка – фотографии движения капли по поверхности. Правая верхняя часть – встреча «блинчика» с дифракционной щелью. Внизу – схема установки. 1 – «блинчик», 2 – траектория его движения, волна, 3 – затухающий всплеск от удара «блинчика» о поверхность, 4 – подтопленная стенка-препятствие, из них сделаны дифракционные щели, 5 – вибростенд.
Силиконовая капля, ведомая волнами на поверхности ведёт себя как квантовая частица. Её прыжки — внутренний колебательный процесс синхронизированный с её «волной де Бройля» соответствующей траектории движения «блинчика» 2 на рисунке.
В местах, где глубина масла меньше (подтопленная стенка 4), стоячие волны затухают и поверхность не может подкидывать «блинчик». Эти участки моделируют препятствия для прыгающей капли (дифракционные щели) не разрушая её. Так был воспроизведен знаменитый двухщелевой эксперимент: собранная статистика поведения капли схожа с таковой у электрона [2].

Статистика отклонений силиконовой капли-блинчика по данным Y. Couder and E. Fort. Single-particle diffraction and interference at a macroscopic scale. Phy. Rev. Lett., 97(15):154101, 2006.
В недавнем посте Путь частицы или волна-пилот наносит ответный удар упоминалось, что более тщательные эксперименты развеяли подобные надежды, а именно, дать наглядную картину корпускулярно-волнового дуализма с помощью прыгающих капелек. Речь шла о работе Томаса Бора (да, внука того самого Нильса Бора, что придумал принцип дополнительности и мистифицировал квантовую механику). Грубо, суть его аргументов сводилась к тому, что дифракционная картина Ива Куде — иллюзия, распределение не фраунгоферовское, а скорее всего просто гауссово и эффекта нет.

По мнению Томаса Бора, случайный разброс (гаусс, рисунок справа) лучше описывает экспериментальные данные, чем дифракция (фраунгофер, слева). И вообще его дед Нильс Бор был во всем прав и непогрешим.
Конечно, прыгающие капли не точное подобие квантовых частиц, однако, они безусловно кандидаты на роль моделей квантовой механики. Ив Куде собрал систему автоколебательную. А про автоколебательные системы известно, что они обладают дискретностью состояний. Очень хорошо об автоколебаниях (картинки, объяснения, код) изложено в посте Автоколебания и резонанс. Детальные исследования системы Ива Куде показали, что у нее много разных режимов, в рассеянии капель есть отличия от картины дифракции электронов, но тем не менее, главное — они в самом деле ведут себя как частицы-волны.
Стоит отметить, что в отечественной науке обсуждались подобные идеи намного раньше, например, в книге томского ученого Б.Н. Родимова «Автоколебательная квантовая механика» [3]. Он тоже сконструировал частицу-волну. К сожалению, его идеи не были подхвачены.
Комментариев нет:
Отправить комментарий