Представим ситуацию: приехали в новый город на неделю-другую, и нужно понять, как выбирать места для обедов. Риски понятны: если постоянно ходить в несколько уже знакомых столовых, то можно упустить совсем хорошую; но и идти в непонятно какую новую столовую вместо хорошей проверенной тоже не хочется. Каждый охотник желает знать, где баланс эксплорейшена-эксплотейшена. Под катом разберемся как нужно действовать.

Сформулируем задачу так:
- Приехали в город на дней, каждый день обедаем в одной из посещенных столовых или идем в новую. Столовых много — хватит хоть каждый день в новую ходить.
- У каждой столовой есть качество — общая численная оценка ее атмосферности, качества еды, цены и прочих параметров. Для неизвестной столовой качество случайно. Качество разных столовых одинаково распределено и независимо.
- Если приходим в столовую, то точно узнаем её качество, но обязательно обедаем в ней.
Цель: максимизировать суммарное качество посещенных столовых за все дни пребывания.
Понятно, что суммарное качество зависит от того, какие столовые попались, поэтому максимизируем его матожидание.
Будем считать, что качество столовой распределено нормально, со средним в нуле. То есть, если качество столовой около нуля — она средненькая; если сильно отрицательное — значит, не очень; если сильно положительное — хороша. В задаче считаем, что мы уже видели много столовых в других городах и представляем распределение качества столовых.
При выборе новой столовой для нас все непосещенные столовые одинаковы, поэтому мы из них не выбираем, просто берем следующую из какого-то списка.
Есть похожие задачи, но они существенно отличаются. В отличие от задачи о разборчивой невесте, к столовым можно возвращаться, а к женихам — нет.
От задачи о многоруком бандите наша отличается тем, что после посещения столовой мы точно знаем ее качество.
Во-первых, понятно, что если мы возвращаемся в одну из посещенных столовых, то нет смысла выбирать не лучшую из них.
Есть еще одно соображение: сначала должна быть фаза исследования столовых, и строго после нее — фаза посещения лучшей. Рассмотрим стратегию, при которой это не так или не всегда так. Тогда на каком-то этапе возникает ситуация, когда мы сначала выбираем лучшую столовую, а потом идем исследовать новую. Но если мы поступим наоборот — сначала посетим новую столовую, а потом пойдем в лучшую, — то наш выигрыш точно не уменьшится, а может даже увеличится, если при проверке новой столовой её качество окажется выше, чем у текущей лучшей.
Соответственно, каждый день нам нужно принимать решение:
- либо пойти искать еще более хорошую столовую, чем лучшая из исследованных;
- либо забить и до конца пребывания в городе ходить в лучшую из найденных.
Из этого становится понятно, что оптимальная стратегия зависит только от уровня лучшей найденной столовой и оставшегося количества дней.
Ясно, что чем качественнее найденная лучшая столовая, тем меньше смысла искать еще более хорошую. Это значит, что для фиксированного оставшегося количества () дней есть порог качественности : если текущий максимум больше, чем , то есть найденная столовая достаточно клевая, мы начинаем ходить только в нее, а если меньше — испытываем судьбу в новой столовой. Получается, что стратегия — это правильный набор чисел .
Первый ход, разумеется, всегда «пойти в новую столовую», потому что вариантов-то и нет.
Эта задача имеет аналитическое решение, но оно довольно громоздкое и нетривиальное, поэтому мы обойдемся меньшей кровью и вычислим эти коэффициенты численно.
Если мы знаем оптимальную стратегию для случая, когда осталось дней, то есть знаем коэффициенты , тогда искать стратегию на дней существенно проще, потому что нужно оптимизировать только одно число.
Зафиксируем текущий максимум и рассмотрим две ситуации:
- Будто мы решили на этом ходу эксплуатировать максимум, а дальше будем действовать по оптимальной стратегии для ходов.
- Будто мы решили пойти в новую столовую, а дальше стали придерживаться оптимальной стратегии для ходов.
Численно проэкспериментируем с каждым вариантом много раз (пока не наберется статистическая значимость) и посмотрим, какой из них дает больший выигрыш. Если первый: значит, оптимальная стратегия для этого m — эксплуатировать максимум, то есть .
Иными словами, для любого m мы можем понять, больше или меньше он, чем . Это позволяет сделать бинарный поиск по — сойдется он к .
А , потому что, когда остался последний день, мы просто выбираем то, что больше: наш текущий максимум или ожидание качества новой столовой, равное нулю.
Таким образом мы можем последовательно вычислить любое . Правда, с уменьшающейся точностью, но для нас это не критично.
Коэффициенты оптимальной стратегии получаются такие: 0, 0,27, 0,43, 0,55, 0,63, 0,71, 0,75, 0,82 и т.д.
Это, конечно, отлично, но давайте разберемся, как их интерпретировать. Чтобы эти коэффициенты получили понятный физический смысл, их нужно перевести в квантили распределения качества столовых, то есть в квантили нормального распределения. Тогда получится: 0,5, 0,61, 0,67, 0,71, 0,74, 0,76, 0,77, 0,79.
Это значит:
- Если остался один день, то искать новую столовую нужно только в том случае, если лучшее, что пока удалось найти, хуже среднего.
- Если осталось еще два дня, то искать новую столовую нужно, если текущая лучшая не попадает в топ 39% = 100% — 61% (61% — вторая квантиль из списка выше).
- Если осталось еще 8 дней и текущая лучшая столовая попадает в топ 21% = 100% — 79% (79% — восьмое число из этого списка), то есть смысл ходить в нее. Если нет, то лучше продолжать искать более хорошую столовую.
- И аналогично для остальных дней.
Выглядит сложновато для практического применения. Сравним с более простыми в использовании стратегиями.
- Во-первых, каждый день можно ходить в новую столовую.
- Можно ходить по столовым «до первой более-менее хорошей», например, из топ 40%. Какие столовые входят в топ 40% мы понимаем, исходя из опыта в других городах.
- Можно первую треть дней ходить по новым столовым, а в оставшиеся ⅔ — в лучшую из найденных.
- Можно каждый третий день идти в новую столовую, а в остальные дни — в лучшую из найденных.
Прогоним 10 000 экспериментов и посмотрим распределение выигрыша для каждой из стратегий. Будем смотреть на периоде в 7 дней и на 30 дней. На графиках по горизонтальной оси — значение выигрыша, по вертикальной — плотность вероятности получить такой выигрыш. В легенде и на вертикальной линии — средний выигрыш стратегии.

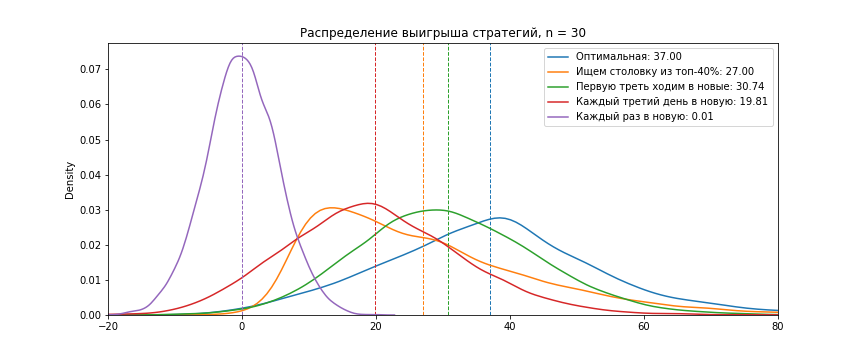
Что тут у нас:
- Средний выигрыш стратегий отличается, но дисперсия на фоне разницы матожиданий большая. Это значит, что удача — один из ключевых факторов.
- Оптимальная стратегия в среднем действительно лучше остальных. Приятно :)
- Стратегии «Искать первую попавшуюся из топ-40%» и «Первую треть времени исследовать» — вполне себе хорошие, не сильно отстают от оптимальной.
- Каждый третий день ходить в новую — в полтора-два раза хуже хороших стратегий. Это значит, что совет «сначала исследовать, а потом эксплуатировать» довольно существенный.
- Если каждый день ходить в новую столовую — получается совсем «по среднему».
- В хорошие столовые нужно возвращаться, это существенно влияет на суммарное качество.
- Лучше сначала сфокусироваться на поиске хорошей столовой, а только потом — на эксплуатации лучшей.
- Удача очень существенно влияет на успех. Хорошо, что на это можно повлиять: подпишитесь на канал и получите два очка удачи бесплатно!
- Остальное не очень важно.
Комментариев нет:
Отправить комментарий