Реальные системы можно рассматривать как линейные только в ограниченном диапазоне нагрузок. Реальный же мир вокруг нас нелинеен (рис. 1). Нелинейность есть нарушение принципа суперпозиции в некотором явлении (механической системе): результат действия суммы факторов не равен сумме результатов от отдельных факторов. Однако по разным причинам, в том числе в связи с отсутствием необходимых знаний, навыков моделирования, необходимого программного обеспечения, инженеры зачастую решают задачи только в линейных постановках. Даже когда линейный подход дает очень большие погрешности. Точное же моделирование поведения системы часто требует проведения нелинейного анализа.
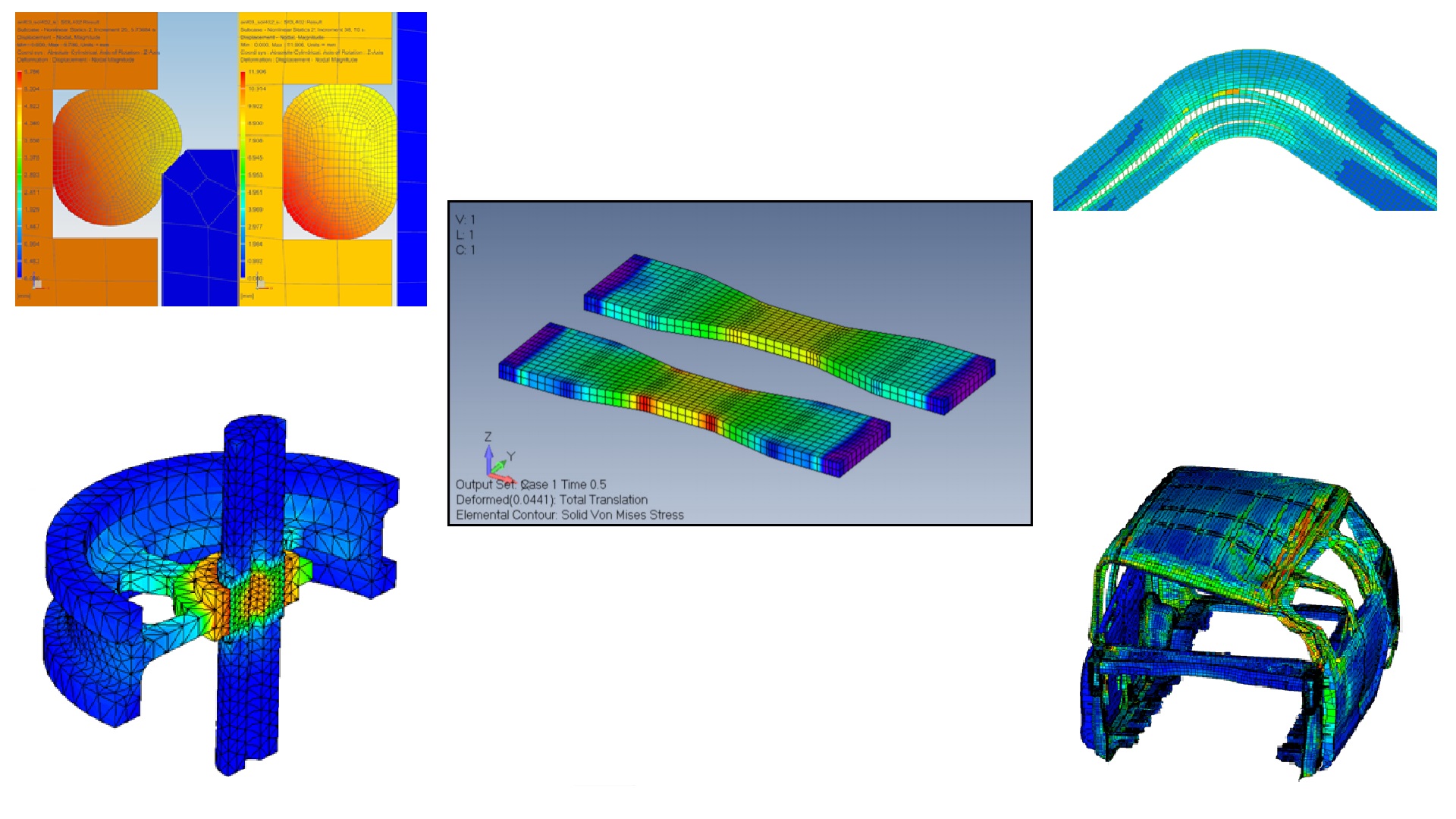
Рис. 1
Введение
Пару месяцев назад я опубликовал статью «Просто о нелинейном анализе методом конечных элементов. На примере кронштейна». В ней я постарался доступно разъяснить минимальный объем терминов и теории, необходимой для осознанного проведения нелинейного статического анализа, подробно разобрал алгоритм решения простой нелинейной задачи. Повторяться не буду, напомню несколько основных положений – и приступим к обзору более сложных явлений, задач механики и инструментов, необходимых для решения этих нелинейных задач.
Линейные допущения часто справедливы, но сегодня при разработке изделий всё чаще необходимо проводить нелинейные расчеты. Чтобы сократить объем экспериментальной отработки, пользователи нуждаются в моделях более высокой точности: уточняются геометрические модели, увеличивается точность физических моделей. Это означает, что учитываются нелинейные эффекты, такие как контакты, большие деформации и свойства материала. Нелинейность задачи может быть обусловлена необходимостью учета истории нагружения конструкции – то есть разложение задачи на составляющие воздействия и последующее объединение результатов невозможны. Без учета этих эффектов решения могут оказаться неточными, что приведет к неверным выводам. Или же изделия могут быть спроектированы с очень большим запасом прочности, а потому станут слишком дорогостоящими.
Классическая физика и математика у нас одна, но в разных расчетных комплексах используются разные наборы алгоритмов и инструментов для решения задач методом конечных элементов. В этой статье я расскажу об инструментах, имеющихся в арсенале пре-постпроцессора Femap с решателем NX Nastran, за более чем 35 лет многократно доказавшим свои надежность, точность и скорость. Для решения самых сложных нелинейных задач, в том числе если необходимо учесть историю нагружения конструкции, подходит модуль многошаговых нелинейных решений Multistep Nonlinear (SOL401 / SOL402).
Контакты и применение сабкейсов
В рамках одного многошагового решения можно изменять условия контакта поверхностей с помощью сабкейсов. Сабкейсы – это отдельные решения, из которых можно сложить общее решение со сложной историей приложения нагрузок, изменения граничных условий. Например, при моделировании сборки можно добавлять или удалять контакты в определенной последовательности.
Трение может быть учтено в настройках контакта, а коэффициент трения – быть постоянным или изменяться в зависимости от скорости, температуры и времени. Детали, которые контактируют, обычно рассматриваются как деформируемые. Но если одна часть намного жестче другой, стоит рассматривать ее как жесткую, чтобы упростить задачу без существенных погрешностей. Это также позволяет применять принудительное перемещение твердого тела на жесткой части в качестве нагрузки.
На рис. 2 изображена модель, в которой резиновое уплотнительное кольцо задано гиперупругим материалом. Моделирование позволяет вычислить напряжения и перемещения в резиновом уплотнительном кольце, используемом для уплотнения крышки, надетой на цилиндр. В целях повышения эффективности модель строится с использованием осевой симметрии. Видимый круг – это поперечное сечение уплотнительного кольца. Размеры кольца уплотнителя в ненапряженном состоянии меньше диаметра цилиндра, поэтому начальное положение уплотнительного кольца показывает, что уплотнительное кольцо и цилиндр частично перекрываются. На первом этапе моделирования при определении контакта производится компенсация перекрытия, то есть уплотнительное кольцо растягивается радиально. Затем колпачок опускается и уплотнительное кольцо деформируется при соприкосновении со стенкой цилиндра. Таким образом образуется уплотнение.

Рис. 2
Геометрические несовершенства конечно-элементной сетки могут быть исправлены путем настройки допусков по зазорам и натягам или путем сглаживания граней. В случае возникновения трудностей со сходимостью есть множество вариантов решения этой проблемы. Например, опция «Нормальная регуляризация» полезна, когда условия контакта включают мягкие материалы, такие как резина. «Тангенциальная регуляризация» позволяет избежать разрывов в силах трения. Кроме того, локальная жесткость и демпфирование в контакте контролируются пользователем, что также может использоваться для улучшения сходимости. В постпроцессоре могут быть проанализированы следующие результаты: контактное давление, расстояние по нормали, скольжение, контактные силы.
Существует множество применений для контактов, включая болтовые соединения, имитацию падения и посадку с натягом. Моделировать болтовые соединения можно с помощью 1D конечных элементов (балки, стержни), 2D (плоские элементы) или 3D-элементов. Преднатяжение можно выполнять с помощью нескольких сабкейсов – например, если нужно смоделировать последовательность затяжки болтов. Сабкейсы преднатяжения могут быть реализованы не только первыми по счету, но и в любой последовательности. При анализе других сабкейсов вычисленные преднапряжения сохраняются, но фактическая нагрузка на болты может изменяться при дальнейшем приложении нагрузок. Пользователи могут анализировать нормальные, сдвиговые напряжения, моменты в болтах – на протяжении всего решения.
На рис. 3 изображена модель, позволяющая проанализировать следующую последовательность сборки/нагрузки/разгрузки: затяжка болта № 1, затяжка болта № 4, затяжка болта № 2, затяжка болта № 3, приложение эксплуатационной нагрузки, снятие нагрузки, снятие затяжки.

Рис. 3
Большие перемещения (деформации) и анализ после потери устойчивости
Большие линейные и угловые перемещения – это фундаментальные нелинейные эффекты (рис. 4). Они учитывают изменение положения нагрузки по мере деформации системы. Также существует эффект изменения жесткости изделия от нагрузки. Решение после потери устойчивости – это нелинейное решение с включенными эффектами больших деформаций.
Нагрузка вызывает потерю жесткости изделия, приводящую к последующим большим деформациям при небольших изменениях нагрузки. Существуют эффективные алгоритмы, позволяющие анализировать систему после превышения критической нагрузки потери устойчивости.

Рис. 4
Анализ после потери устойчивости – это особый тип статического сабкейса в Femap. В стандартном квазистатическом анализе нагрузки увеличиваются в соответствии с законом, определенным пользователем. Но некоторые изделия неустойчивы из-за их формы после достижения определенного уровня нагрузки. Такие изделия скачкообразно теряют жесткость в некотором диапазоне нагрузок. Для решения подобного рода задач следует использовать алгоритм «длины дуги» (arc length) – с его помощью решают задачи неустойчивого изгиба, потери устойчивости. Решение позволяет не только определить критическую нагрузку потери устойчивости на изгиб, но и проанализировать, как будет вести себя конструкция после того как она потеряет устойчивость. Вместо изменения нагрузок, основанных на временном приращении, алгоритм автоматически изменяет приращения нагрузки пропорционально перемещениям, а не времени.
Начальные несовершенства формы оказывают в задачах потери устойчивости большое влияние. Несовершенства формы могут быть учтены как искривления в геометрии/сетке, что можно использовать для учета несовершенств производственного процесса. Пользователь может моделировать места преднамеренного изгиба или моделировать повреждения, полученные в ходе эксплуатации.
Физическая нелинейность (нелинейность свойств материалов). Пластичность, гиперупругость, вязкость, ползучесть и композиты
В традиционном линейном анализе все материалы рассматриваются как линейные и упругие. Многошаговый нелинейный решатель Femap поддерживает нелинейные свойства совместно с изотропным, ортотропным, анизотропным поведением. Также поддерживаются еще несколько нелинейных моделей поведения материала, включая пластичность, гиперупругость, ползучесть и повреждение (damage). Пользователям, которым требуется задать уникальные свойства материалов, предоставлена возможность дополнительно добавлять собственные модели материалов.
Пластичные модели материалов с различными настройками доступны для моделирования. Пользователи могут задать кривую напряжений-деформаций как билинейную или полилинейную (рис. 5). Эффекты нагрузки/разгрузки могут быть описаны с помощью изотропных, кинематических или смешанных моделей упрочнения. Кривые напряжений-деформаций также могут быть дополнены температурной зависимостью. Таким образом материалы, зависимость свойств которых от температуры необходимо учесть при решении задачи, могут быть описаны адекватно.

Рис. 5
Гиперупругие материалы благодаря своим свойствам широко используются в различных отраслях. Они не зависят от скорости деформации. К таким материалам относятся резина, пена, биологические и полимерные материалы. Они поддерживают очень большие деформации (более 600%), практически несжимаемы, а также для них могут быть заданы температурные зависимости. Доступны стандартные модели материалов Муни-Ривлина (Mooney-Rivlin), Огдена (Ogden) с эффектом Муллинса (Mullins) и модели пенопласта. На рис. 6 изображена модель кожуха рукоятки переключения передач. Материал кожуха задан как гиперупругий резиновый материал с использованием модели Муни-Ривлина. Поверхности кожуха настроены для самоконтакта.

Рис. 6
Вязкоупругие материалы – это упругие материалы, обладающие способностью рассеивания механической энергии из-за влияния вязкости.
Эластичные материалы, такие как резина, растягиваются мгновенно и быстро возвращаются в исходное состояние после снятия нагрузки. Вязкость (внутреннее трение) – это свойство тела оказывать сопротивление перемещению одной его части относительно другой. Femap поддерживает вязкоупругие материалы с формулировками серий Кельвина и Прони. Модель Кельвина отражает явление упругого последействия, которое представляет собой изменение упругой деформации во времени, когда она или постоянно нарастает до некоторого предела после приложения нагрузки, или постепенно уменьшается после ее снятия (рис. 7). Когда снимается напряжение, материал постепенно расслабляется до недеформированной стадии. Модель Кельвина применяется для органических полимеров, резины, дерева при невысокой нагрузке.

Рис. 7
Деформации типа ползучести происходят с течением времени без какого-либо изменения нагрузки. Деформация при ползучести, как и при пластичности, является необратимой (неупругой), поведение материала при ползучести несжимаемое.
Многие материалы, особенно в условиях высокой температуры, могут испытывать деформации типа ползучести. Femap использует стандартную модель ползучести Бейли-Нортона и позволяет задавать температурные зависимости для определяющих коэффициентов.
В большинстве материалов при действии постоянной нагрузки выделяют три стадии ползучести (рис. 8). На первой стадии скорость деформации уменьшается со временем. Это явление наблюдается в течение короткого периода времени. Вторая стадия, более длительная, характеризуется постоянным значением скорости деформации. На третьей стадии скорость деформации быстро увеличивается вплоть до полного разрушения материала (разрыва образца).

Рис. 8
Многошаговый нелинейный решатель Femap может моделировать нелинейное поведение композиционных материалов в результате внутрислоевого или межслоевого разрушения (рис. 9).
В случае внутрислоевого разрушения отдельные слои ослабевают и теряют жесткость при превышении определенного уровня нагрузки. Решатель отслеживает жесткость каждого слоя в изделии и обновляет жесткость элемента по мере того как слои становятся более поврежденными. В крайнем случае может произойти полная потеря жесткости в элементе. Внутрислоевые разрушения (для однонаправленного или тканого слоя) бывают различных типов: разрушение волокон, разрушение матрицы, разрушение связей между матрицей и волокнами.
При межслоевом разрушении связь между слоями изделия может ослабнуть и потерять жесткость. Femap использует связующие элементы для моделирования такого поведения. Моделирование показывает области, где связь теряется и слои могут отделяться.

Рис. 9
Учет истории нагружения. Многошаговые решения с применением сабкейсов
Состояние конструкции в некоторых случаях зависит от последовательности приложения нагрузок, то есть нелинейность задачи может быть обусловлена необходимостью учета истории нагружения конструкции. Есть задачи, в которых достаточно учесть исходное напряженно-деформированное состояние (часто для нелинейностей, связанных с поведением материала). Но иногда бывает необходимо учесть сложную историю нагружения, состоящую из нескольких сабкейсов с изменяющимися силовыми факторами и граничными условиями. Граничные условия могут меняться при изменении площадок контакта.
Важной особенностью многошагового нелинейного решателя Femap является то, что он может поддерживать несколько сабкейсов и выполнять различные решения – такие как статические, динамические, модальные в отдельных сабкейсах в рамках одного решения. В дополнение к изменению типа анализа в сабкейсах также можно изменять настройки параметров и граничные условия. Это открывает пользователям большие возможности настройки решений. Вот типовой сценарий с использованием сабкейсов: каждый сабкейс начинается с условий, в которых закончился предыдущий сабкейс. Такой сабкейс называется последовательным. Но пользователь также может начать решение снова и не в последовательном сабкейсе.
На рис. 10 показан пример моделирования трех компонентов авиационного двигателя: два фланца и ступица соединены болтами в несколько этапов. Для эффективного решения используется симметричный сектор модели. На первом этапе анализируются отклонения от пресс-формы для одного фланца и ступицы. На втором два болта затягиваются, чтобы соединить фланец и ступицу. На третьем рассматривается запрессовка второго фланца. На четвертом затягиваются еще два болта, чтобы соединить второй фланец и ступицу. Затем, на пятом этапе, анализируется нагрузка от высокоскоростного вращения полностью соединенных деталей. Последним шагом является модальный анализ – он используется для прогнозирования напряжений от вибрации. Этот полный набор из шести шагов может быть выполнен в рамках одного анализа, что позволяет получить богатый набор данных для понимания напряженно-деформированного состояния двигателя.

Рис. 10
В дополнение к статическим сабкейсам поддерживаются динамические (transient). Этот тип сабкейса может начинать решение или следовать за статическими сабкейсами (рис. 11). При запуске решения могут быть применены начальные условия в форме перемещений или скорости. Например, для моделирования падения рационально начинать решение с точки непосредственно перед ударом и задавать начальную скорость, равную скорости удара. Если динамический анализ следует за статическим или другим динамическим анализом, то отклонения, скорости, ускорения в начале сабкейса будут такими же, как в конце предыдущего сабкейса.
В динамическом сабкейсе сгенерированные силы инерции, демпфирование, матрица жесткости и силы уравновешены приложенными нагрузками. Силы инерции можно отключить при анализе переходных процессов. Это очень полезно для ускорения решения и перехода к стационарному состоянию.

Рис. 11
Динамический анализ и моделирование кинематических связей
Моделирование падения часто выполняется для электронных приборов, чтобы понять, насколько хорошо они переживут столкновение с землей. На рис. 12 отображен ударный процесс, возникающий при падении тепловизионной камеры. Материал корпуса из поликарбоната моделируется как упругопластичный материал, а внутренняя печатная плата и электронные компоненты – как линейно-упругие материалы. Динамический анализ начинается с точки соприкосновения тепловизора с землей. Камере задается начальная скорость, соответствующая высоте, с которой она была сброшена (в данном случае это высота 1 метр). Камера быстро соприкасается с землей и отскакивает. Анализируются напряжения и деформации корпуса и бортов.

Рис. 12
Femap поддерживает применение кинематических связей для соединения различных частей сборки. Поддерживаются основные типы шарниров, такие как цилиндрические, сферические шарниры, жесткие и гибкие направляющие.
На рис. 13 изображен процесс развертывания солнечных панелей спутника, соединенных посредством цилиндрического шарнира. С помощью данной модели можно оценить вибрации и определить уровень напряжений.

Рис. 13
Заключение
Главными критериями качества для оценки расчетной модели и полученных результатов всегда были и будут сравнение с натурными экспериментами и аналитическими решениями. Нелинейные модели не являются исключением из правил. Разработчики Femap из компании Siemens проверяют нелинейные формулировки с помощью тестов NAFEMS (Международная ассоциация инженерного моделирования и анализа) и аналитических решений.
В дополнение к проверке формулировок, алгоритмы регулярно тестируются с помощью большой библиотеки тестовых моделей, чтобы избежать появления ошибок по мере добавления улучшений и расширений.
Однако перед каждым инженером каждый раз встает вопрос адекватности принятых допущений, правильного использования имеющихся программных инструментов и многокритериальной оценки полученных результатов.
В данной статье предложен обзор актуальных нелинейных задач и инструментов для их решения. Безусловно, этой информации недостаточно, чтобы на практике приступить к решению вышеобозначенных задач. Поэтому приглашаю вас на бесплатный вебинар «Femap и возможности модуля многошаговых нелинейных решений Multistep Nonlinear», который состоится 19 ноября 2020 года в 12:00. Во второй половине вебинара я решу задачу растяжения металлического образца с учетом пластичности и изотропного упрочнения материала.
Ознакомиться с обзором возможностей расчетного комплекса Femap с NX Nastran можно здесь, а скачать бесплатную пробную версию Femap с NX Nastran – здесь.
Филипп Титаренко,
продакт-менеджер по направлению Femap
АО «Нанософт»
E-mail: titarenko@nanocad.ru
Литература
1. Femap с NX Nastran, Simcenter 3D Многошаговые нелинейные решатели: SOL401 / SOL402.Multistep Nonlinear (перевод Ф.В. Титаренко). Siemens.
2. NX Nastran Handbook of Nonlinear Analysis (Solutions 106 and 129). Siemens.

Комментариев нет:
Отправить комментарий