
Кадр из фильма "Иван Васильевич меняет профессию"
Помните этот момент из легендарного произведения Гайдая? Удивительно, насколько по-разному может восприниматься один и тот же человек с одним и тем же лицом. А когда речь идет о миллионах разных людей и нужно найти одного единственного — даже человек уже бессилен, а сверточные нейросети продолжают справляться. Такое большое количество лиц вынуждает искать новые подходы к разграничению. Один из таких подходов — модификации функций потерь, которые помогают нам не потонуть в огромных датасетах при распознавании лиц, довольно точно определяя, кто есть кто.
Под катом мы рассмотрим различные модификации кросс-энтропии для задачи распознавания лиц.
Немного терминологии в контексте нашей задачи:
- Бэкбон (backbone) — некий черный ящик, сверточная сеть, входом которой является изображение лица, а выходом — вектор, представляющий лицо. Примером может быть бэкбон из известного в узких кругах InsightFace — Open Source решения для распознавания лиц с достаточно высоким качеством работы.
- Вектор лица (embedding) — вектор, представляющий лицо в многомерном пространстве. Размерность пространства обычно находится в пределах от 128 до 512. В нашей статье зафиксируем размерность вектора константой, равной 512. К векторам лиц мы предъявляем следующее требование: мы хотим их удобно сравнивать на основе некого расстояния между векторами. Другими словами, мы хотим, чтобы расстояние между векторами лиц одного человека было маленьким, а между векторами разных людей — большим. Для этого требуем, чтобы скалярное произведение двух нормализованных векторов лиц (расстояние между векторами) одного и того же человека было бы как можно ближе к 1, а разных — к -1 (ну или хотя бы 0).
- Embedding-слой — полносвязный слой, является последним и выходным слоем бэкбона, его размерность (количество нейронов) равна размерности вектора лица.
- Слой классификации — полносвязный слой, который иногда (зависит от функции потерь) следует за бэкбоном, его цель — из вектора лица получить вектор вероятностей для классов, где каждый класс — один человек. В общем случае его результат это , где — вектор лица (выход бэкбона), — веса полносвязного слоя, а — свободный член. Переход от значений слоя к вероятностям обычно делается оператором softmax.
Задача распознавания лиц сводится к тренировке такого бэкбона, который обеспечит нас удобными векторами лиц, которые мы сможем сравнить. Для тренировки используется функция потерь — математическая функция, которая говорит, насколько хорошо наша текущая сеть справляется с задачей. Значение функции — штраф (чем он меньше — тем лучше), а переменные — параметры сети. Именно про функции потерь и их эволюцию в задаче распознавания лиц мы сегодня поговорим.
Исторически в глубоких сверточных нейросетях существует два основных подхода к задаче распознавания лиц: обучение метрики (metric learning) и классификация.
Обучение метрики
В случае обучения метрики, мы заставляем сеть увеличивать расстояние между фотографиями разных людей и уменьшать его между фотографиями одного и того же человека. Самый известный пример — Triplet Loss:
где:
- — anchor, вектор лица человека, с ним сравниваются два других вектора;
- — positive, вектор другого изображения того же человека;
- — negative, вектор лица другого человека;
- — некая константа, которая отвечает за минимальное расстояние между позитивной и негативной парами.
Таким образом, мы хотим, чтобы расстояние между фотографиями одного человека было как минимум на меньше расстояния между фотографией того же человека и какого-то другого.
Классификация
Добавляем к нашему бэкбону полносвязный слой для классификации, обучаем сеть классифицировать людей (каждый класс — отдельный человек), затем удаляем этот слой, и оказывается, что embedding-слой удовлетворяет нашим требованиям.
Идея Triplet Loss красивая и напрямую соответствует нашей задаче, а классификация отдает немного “кашей из топора”, но так вышло, что качество второго подхода лучше, все SotA обучены этим подходом, и основное развитие идей пошло по этому пути. Однако, Triplet Loss до сих пор можно использовать для дообучения (fine-tuning) модели. Так как нам интересен подход с лучшим качеством, рассмотрим подробней второй вариант и проследим историю развития идей.
Рассмотрим подробнее, что происходит, когда мы обучаем модель классифицировать людей, и почему потом можно использовать вектора лиц из, по сути, промежуточного слоя. На верхнем уровне путь от изображения лица до предсказания человека выглядит так:
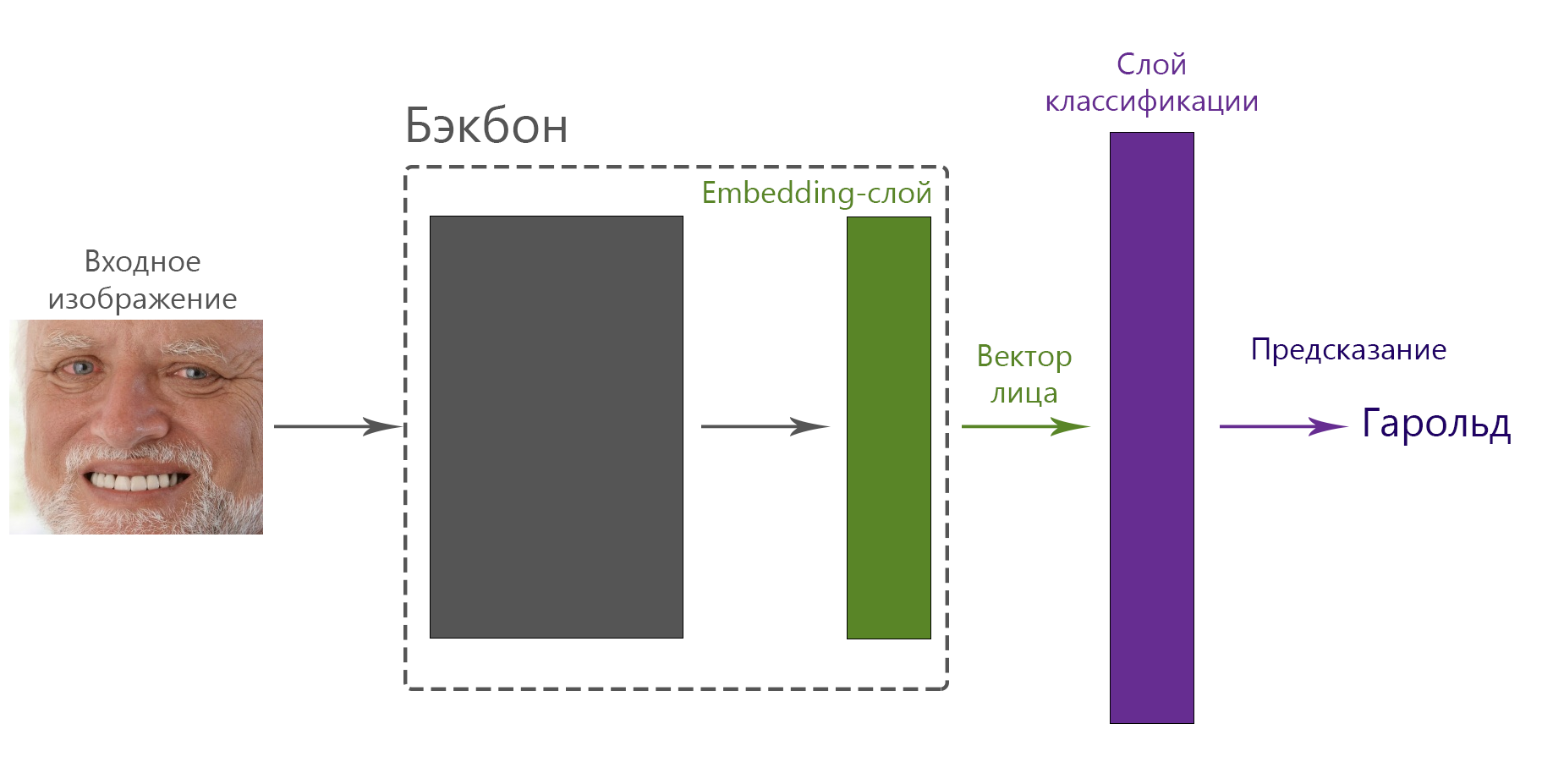
Веса слоя классификации — это двумерная матрица, где первая размерность отвечает за вектор лица (в нашем случае 512), а вторая — за количество классов (зависит от датасета, обычно десятки или сотни тысяч). Другими словами — для каждого класса (человека) есть некий вектор, размерность которого равна размерности вектора лица. Этот вектор обычно называется центроид, то есть некий “средний вектор” конкретного человека. Весь процесс обучения теперь выглядит так: дай мне такой вектор фотографии, чтобы ближайшим из всех центроидов оказался центроид, соответствующий человеку на фотографии. Центроиды не фиксированы и изменяются в процессе обучения. Если рассматривать веса слоя классификации, то это будет выглядеть примерно так:

У классификации есть огромный плюс: каждое изображение мы сравниваем за один раз с десятками тысяч других изображений, а минус заключается в том, что это не то чтобы изображения, а некоторая обучаемая нами усредненная сущность человека. Несмотря на это, полученная модель хорошо учится отличать именно лица. Более того, время обучения остается контролируемым, в отличие от Triplet Loss — когда имеем дело с уже неплохой моделью, становится крайне сложно искать тройки изображений, на которых сеть ошибается (hard sampling), поэтому обучение сети стремительно замедляется.
Просто посчитать дистанции от входного изображения до каждого из центроидов недостаточно — непонятно, как нам за это штрафовать, поэтому для полноты картины нам не хватает двух типичных для классификации составляющих: Softmax для перехода от расстояний к вероятностям предсказаний и Cross Entropy — для вычисления штрафа. В литературе они часто идут вместе и называются объединённо Softmax Loss.
Начнем с Softmax, который переводит полученные дистанции в вероятности предсказания. Введем обозначения:
- — веса слоя классификации (центроиды)
- — выход embedding-слоя, вектор входного изображения
- — bias, свободный член
Таким образом, выход слоя классификации (ни у него, ни у embedding-слоя нет активаций): . Функция Softmax() выглядит следующим образом:
Следующий шаг — добавить Cross Entropy, итоговый Softmax Loss имеет следующий вид:
Где — индекс центроида нашего класса. Например, если на входе у нас фото Гарольда, и индекс класса Гарольда 42, то мы берем 42-ю строку в весах слоя классификации.
Все это — классика и известно давно, а дальше самое интересное.
Еще раз посмотрим на выход слоя классификации: Чтобы свободный член не мешался — уберем его: , получаем . Данное произведение является не чем иным, как скалярным произведением вектора лица на каждый из центроидов. Разберемся с размерностями:
После умножения на получаем матрицу размером , то есть результат умножения каждого входного изображения на каждый из центроидов.
Теперь вспомним, как выглядит формула косинуса угла между двух векторов:
Это как раз то, что нам нужно: угол между конкретным центроидом и вектором лица — это скалярное произведение, деленное на две нормы. Нам мешают нормы векторов, чтобы это исправить, сделаем норму каждого центроида равной единице (), а норму приравняем к некоторой константе s (scale), таким образом:
Scale — наш первый из двух гиперпараметров. Фиксирование его для всех векторов приводит к тому, что они теперь располагаются на гиперсфере. В 2D варианте это выглядит примерно так (один цвет — один класс):

Изображение из статьи ArcFace, игрушечный пример для демонстрации: каждый класс выделен своим цветом, каждая точка на окружности — отдельно взятое изображение, средний вектор каждого класса соединен с центром для наглядности. Обратим внимание, что классы соединены "без зазоров".
Перепишем Softmax Loss (теперь это называется Normalized Softmax Loss, N-Softmax) с учетом этих наблюдений:
Мы разделили сумму в знаменателе на два слагаемых для удобства дальнейшего объяснения. На основе N-Softmax основаны все основные функции потерь для распознавания лиц.
Итак, у нас есть некие центроиды и текущий вектор лица, а после слоя классификации — косинусы углов между ними. Если мы будем обучать с обычным softmax loss, то сети будет достаточно просто разделить классы между собой. Другими словами, у каждого человека есть свое пространство (decision boundary), в которое должны попадать все вектора его лиц (в идеальном случае). Границы этих пространств могут быть близки друг к другу. Почему это проблема? Потому что расстояние (угол) между изображениями на границах близких классов может быть меньше, чем расстояние между некоторыми изображениями одного класса. Тут возникает идея — давайте добавим между этими пространствами некоторую пустую область (decision margin). Размер этой области — margin — второй главный гиперпараметр наших функций потерь, о первом мы говорили ранее: scale — норма вектора лица. Графически на нашей 2D гиперсфере это выглядит так (рисунок из статьи ArcFace):

Слева — без margin, справа — с margin
Теперь между нашими классами есть пустая область, и граничные изображения одного класса далеко до изображений других классов.
Так как мы говорим об углах между векторами, margin (обозначим для краткости ) можно добавить в три места в функцию потерь:
-
Домножить на угол. То есть для позитивного случая вместо будет . Этот метод используют две работы: Large-Margin Softmax Loss и SphereFace. Этот подход не хватает звезд с неба, и интересен скорее с исторической точки зрения, так как был первым вариантом Margin-based loss. Функция потерь выглядит следующим образом:
-
Отнять margin от косинуса угла. Теперь вместо у нас для позитивного случая. Про это тоже две основных работы: AM-Softmax и CosFace , что порождает некоторую путаницу, так как встречаются оба названия, но обе статьи про одно и то же. Функция потерь:
-
Прибавить margin непосредственно к углу: → . Эта идея показана в ArcFace. Функция потерь ArcFace имеет следующий вид:
-
Хочется отметить еще один вариант, он является развитием идеи ArcFace и называется AirFace. Margin так же, как и у ArcFace, добавляем к углу, но уходим от косинуса угла непосредственно к самому углу (). Чем дальше векторы друг от друга, тем больше угол, а нас это не особо устраивает (почему — будет ниже), поэтому авторы добавляют немного эвристики, и теперь у нас не просто , а , и итоговая функция потерь имеет следующий вид:
Три разновидности добавления margin — добавление к углу, к косинусу угла и домножение на угол — легли в основу многих модификаций (особенно ArcFace).
Мы более-менее разобрались, в чем идея развития функций потерь для распознавания лиц, но у нас есть два гиперпараметра — scale (s) и margin (m), влияние которых пока не очевидно. Например, в статье AM Softmax предлагается брать , а , в ArcFace — , a , а в CosFace (напомним, идея та же, что и AM Softmax) , a . В каждой статье приведены теоретические обоснования, почему параметры такие, но в целом это скорее “подобрали эмпирически”, о чем авторы честно пишут.
Тут на сцену выходит еще одна работа — AdaCos, основная идея которой — исследовать влияние scale и margin на предсказанную вероятность позитивного случая. Основные постулаты следующие:
- Margin и scale зависят от количества классов — вполне логичное умозаключение, о чем в предыдущих работах не особо упоминалось.
- Авторы делают вывод о зависимости параметров scale и margin, фиксируют margin и смотрят влияние scale.
- Предлагается формула для вычисления scale в зависимости от количества классов.
- Авторы предлагают два варианта обучения — с фиксированным и изменяемым scale
В статье есть красивые графики для 2 тысяч и для 20 тысяч классов, приведем их без изменений, по оси Y у нас предсказание — вероятность, что фото относится к своему классу, а по X — угол между центроидом и вектором лица. Чем меньше вероятность, тем больше штраф, если вероятность равна единице, то штрафа нет:

В верхнем ряду показано влияние scale (у авторов явно не указано, но можно предположить, что margin фиксирован и равен 0), в то время как в нижнем — margin при scale=30. Как видно, чем больше scale, тем “резче” ступенька, а margin двигает ее вдоль оси X. Очевидно, что одинаково плохи граничные случаи — слишком большие и слишком малые scale и margin, и истина где-то посередине, но где? В AdaCos предлагается выбор scale на основе количества классов (на графиках выше изображено пунктиром). Пропуская вывод, к которому есть вопросы: , где — количество классов. На основе этой формулы для большинства задач распознавания лиц s попадает примерно в диапазон [10, 25], что значительно меньше предлагаемых ранее.
Последнее нововведение работы AdaCos — динамичное изменение scale. В основном, scale уменьшается, формула пересчета основана на среднем угле в батче. В результатах, приведенных в статье, это улучшает качество.
Мы можем двигать margin куда и как угодно, но как это работает, и почему у нас есть разница между вариантами, и есть ли вообще? Разберем академический подход и построим зависимость целевого значения от угла для позитивного случая. По оси X берем угол между центроидом и вектором лица, а по оси Y — полученное значение функции с учетом наших манипуляций (для обычного N-softmax это будет ):

Из интересного: CosFace ожидаемо просто сдвигает N-softmax вниз, а ArcFace — влево. SphereFace, согласно оригинальной идее имеет смысл в пределах , в нашем случае до . У ArcFace есть неприятный хвостик — с увеличением угла увеличивается target logit, что не очень хорошо, так как на этом участке чем больше угол, тем лучше. Другими словами, мы отдаляем фотографии человека от его центроида, если они в зоне этого хвоста (угол больше ). Про этот момент в оригинальной статье не особо сказано, но при этом в реализациях (например, тут) есть небольшой интересный кусок кода, который его исправляет:
# cosine - cos(theta) # phi - cos(theta + m) # th - cos(math.pi - m) # mm - sin(math.pi - m) * m if easy_margin: phi = torch.where(cosine > 0, phi, cosine) else: phi = torch.where(cosine > th, phi, cosine - mm)Нечто под названием easy_margin и его антагонист направлены именно на устранение хвоста, графически это выглядит так:

Easy margin заменяет поведение во всей зоне, где угол между вектором текущего лица и центроида больше на обычный N-Softmax (), а not easy margin меняет только проблемный кусок. Однако, как показывает практика, даже случайная инициализация приводит к тому, что медиана углов находится в , и даже негативные кейсы очень редко попадают в зону “хвоста”, а позитивные так и вовсе в качестве исключения, так что это дополнение мало сказывается на результате, но учесть это будет не лишним.
Численные оценки качества приведены в каждой из работ, но для чистоты возьмем только независимые обзоры. Если коротко — "в среднем" побеждает ArcFace. Например, в обзорной статье показано (таблицы 4 и 8 в работе):
В другом обзоре тенденция та же (рисунок 3 в работе), тесты на LFW, заголовок столбца — бэкбон-тренировочный датасет:
Авторы приходят к выводу, что ArcFace является SotA в вопросе функций потерь.
Мы рассмотрели основные варианты функций потерь для задачи распознавания лиц. Все они заключается в добавлении дополнительного пространства между классами (margin) к предсказаниям сети, что позволяет значительно повысить качество. Из существующих вариантов стоит отметить AM Softmax (за счет простоты и очевидности) и ArcFace (лучшие результаты по большинству тестов). Для небольших сетей, где важна скорость, и не так важны десятые процента точности, можно рассмотреть AirFace.
Функции потерь:
SphereFace https://arxiv.org/abs/1704.08063
AM Softmax https://arxiv.org/abs/1801.05599
CosFace https://arxiv.org/abs/1801.09414
ArcFace https://arxiv.org/abs/1801.07698
AirFace https://arxiv.org/abs/1907.12256
Обзоры:
Deep Face Recognition: A Survey https://arxiv.org/abs/1804.06655
A Performance Evaluation of Loss Functions for Deep Face Recognition https://arxiv.org/abs/1901.05903
Комментариев нет:
Отправить комментарий