
Мы все так привыкли к облачной синхронизации Dropbox и совместному редактированию в Google Docs, что объединение результатов действий разных пользователей может казаться давно решённой проблемой. Но на самом деле в этом вопросе остаётся множество подводных камней, а работа над алгоритмами CRDT вовсю продолжается.
Один из людей, ведущих эту работу — Мартин Клеппманн (Martin Kleppmann): исследователь в Кембриджском университете и создатель популярной библиотеки Automerge. И на конференции Hydra он рассказывал о нескольких вещах, которые исследовал буквально в последнюю пару лет. Какие действия пользователя могут заставить Google Drive выдать «unknown error»? Почему в CRDT метаданные о работе над документов могут занимать в сто раз больше места, чем сам документ, и как с этим бороться? А у какой проблемы сейчас даже не существует известного решения?
Обо всём этом он поведал в докладе, а теперь мы сделали для Хабра текстовый перевод. Видео и перевод — под катом, далее повествование будет от лица спикера.
Содержание доклада
Сегодня я хотел бы рассказать вам о CRDT (Conflict-free Replicated Data Types, бесконфликтные реплицированные типы данных). Вначале мы вкратце выясним, что же это такое и зачем они нам нужны, но в основном будет новый материал на основе исследований, которые мы проводили последний год или два. Возможно, вы читали мою книгу. Но сегодня речь пойдёт о ПО для совместной работы (collaborative software).
ПО для совместной работы
С помощью такого ПО несколько пользователей могут участвовать в редактировании и обновлении общего документа, файла, базы данных или какого-либо другого состояния. Примеров такого ПО много. С помощью Google Docs или Office 365 можно совместно редактировать текстовые документы. Среди графических приложений ту же функциональность даёт Figma. Trello позволяет пользователям давать друг другу задания, комментировать их и тому подобное. Общим у всех этих приложений является то, что в них пользователи могут параллельно обновлять данные.
В качестве примера рассмотрю редактирование текста (но те же механизмы работают для довольно широкого спектра приложений).
В редакторе текста для совместной работы два пользователя могут почти одновременно внести изменения в документ, при этом не видя изменений друг друга. Предположим, есть документ, состоящий из слова «Hello!». Красный пользователь добавляет перед восклицательным знаком слово «World», а параллельно с ним синий пользователь добавляет после восклицательного знака смайлик:
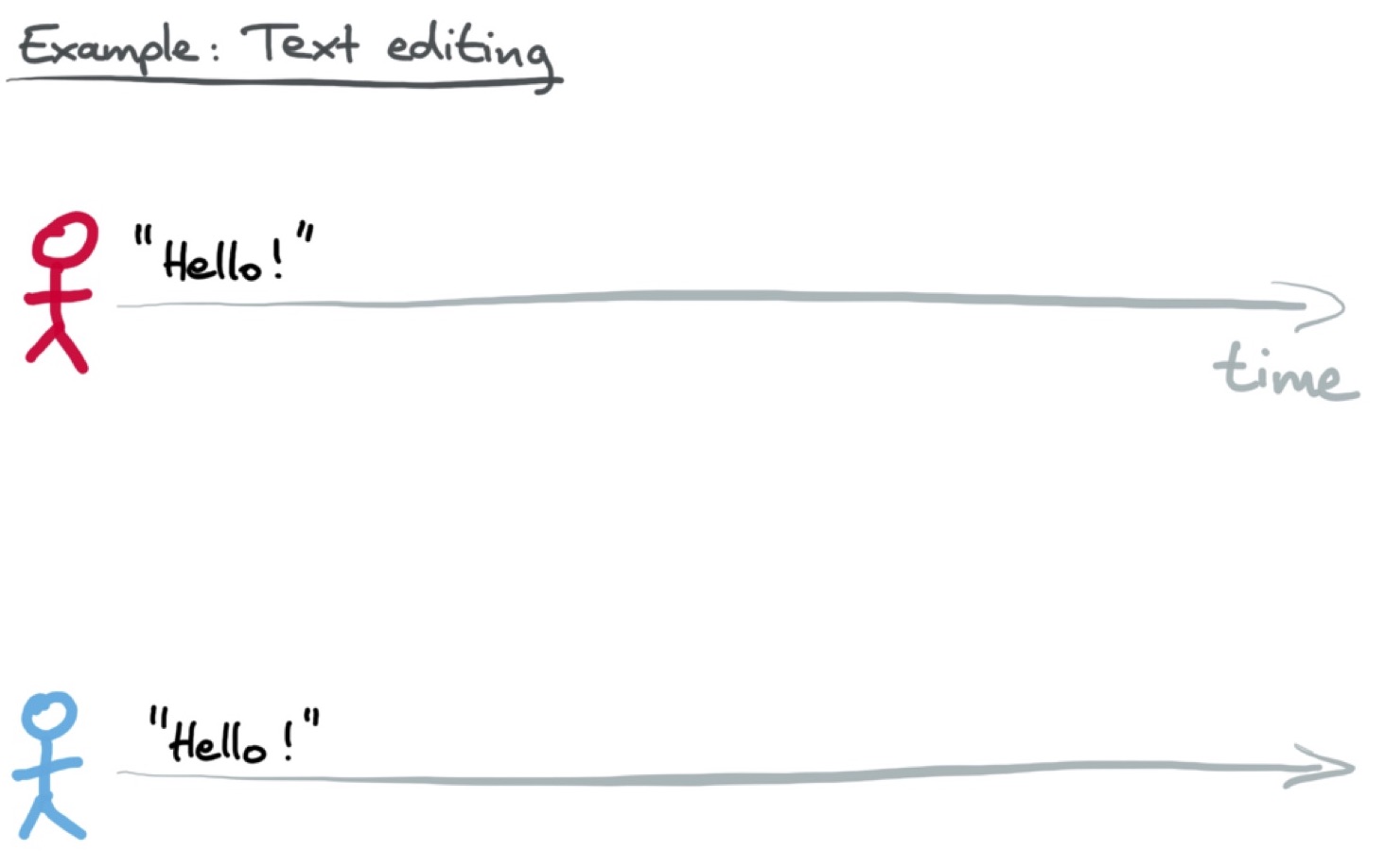
Необходимо обеспечить, чтобы при подключении к сети документ обоих пользователей пришёл к одинаковому состоянию, отражающему все внесённые изменения. В нашем случае документ будет выглядеть так: «Hello World! :-)».
Алгоритмы для параллельного редактирования документов
Для обеспечения подобного параллельного редактирования было разработано множество алгоритмов. Расхождения между версиями документа могут возникнуть, даже когда оба пользователя в онлайне, если они редактируют документ одновременно. А когда работа идёт в офлайне, расхождений будет ещё больше. Представьте, сколько изменений накапливается после нескольких часов редактирования текста. При такой работе постоянно происходят ветвления и слияния вариантов документа, как в системе контроля версий вроде Git. Как правило, системы для совместной работы должны выполнять разрешение конфликтов автоматически, чтобы это не приходилось делать вручную.
На самом общем уровне можно различить два вида алгоритмов, обеспечивающих параллельное редактирование документов:
- Давно существует семейство алгоритмов операционального преобразования (operational transformation, OT), используемых в Google Docs и многих других современных приложениях.
- А примерно 15 лет назад появился более новый вид: CRDT.
Оба вида алгоритмов решают примерно одну и ту же проблему, но существенно разными способами.
Рассмотрим вкратце механизм работы операционального преобразования. Предположим, существует документ, состоящий из букв «Helo», к которому есть доступ у двух пользователей. Один пользователь добавляет в документ вторую букву «l», а другой — восклицательный знак. Теперь необходимо объединить эти версии документа:
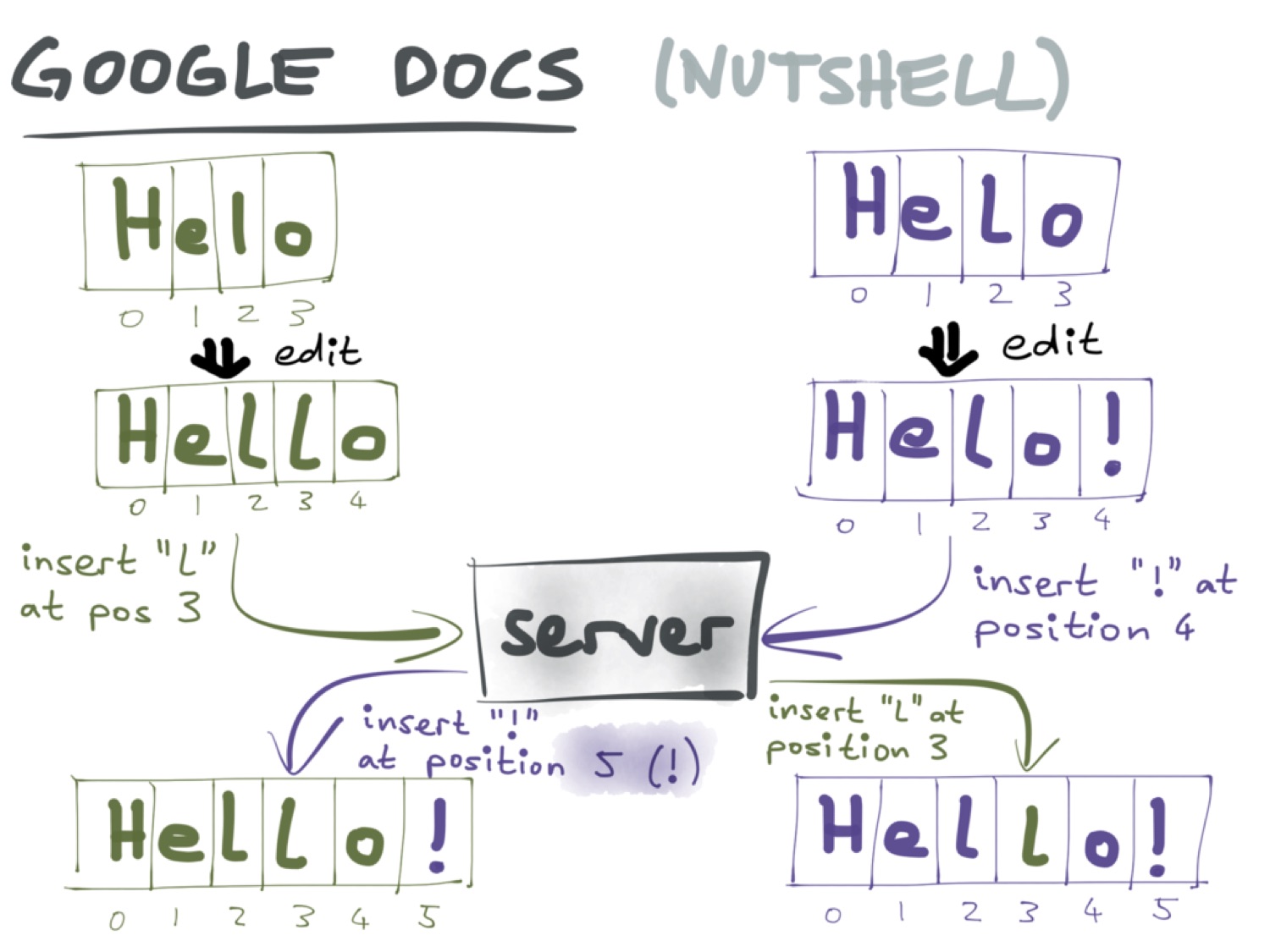
При операциональном преобразовании каждое изменение записывается как операция. Операция — это добавление или удаление символа в документе. Поэтому необходим способ указать, где именно произошло это изменение. В операциональном преобразовании для этого используется индекс символа. В случае нашего документа индекс новой «l» — 3, а восклицательного знака — 4.
В какой-то момент пользователи обмениваются изменениями через сервер. Второй пользователь узнаёт, что по индексу 3 необходимо вставить букву «l», и получает необходимый результат. Но в случае с первым пользователем всё несколько менее очевидно. Если просто добавить восклицательный знак по индексу 4, то получится «Hell!o», поскольку первый пользователь до этого добавил новый символ по индексу 3, и из-за этого индексы всех последующих символов увеличились на единицу. Поэтому индекс 4 необходимо преобразовать в индекс 5. Отсюда название алгоритма — операциональное преобразование. И отсюда же главная сложность с ним.
Большинство алгоритмов операционального преобразования исходят из предположения о том, что все взаимодействия выполняются через единый сервер. Даже если пользователи сидят в одной комнате и могли бы передать друг другу свои версии по Bluetooth, им всё равно нужно связаться с сервером (который в случае Google Docs предоставляет им Google). Этот алгоритм правилен только в том случае, если все изменения упорядочены одним сервером. А следовательно, любые другие каналы обмена информацией не допускаются, даже если технически доступны — будь то Bluetooth, P2P или банальная флешка.
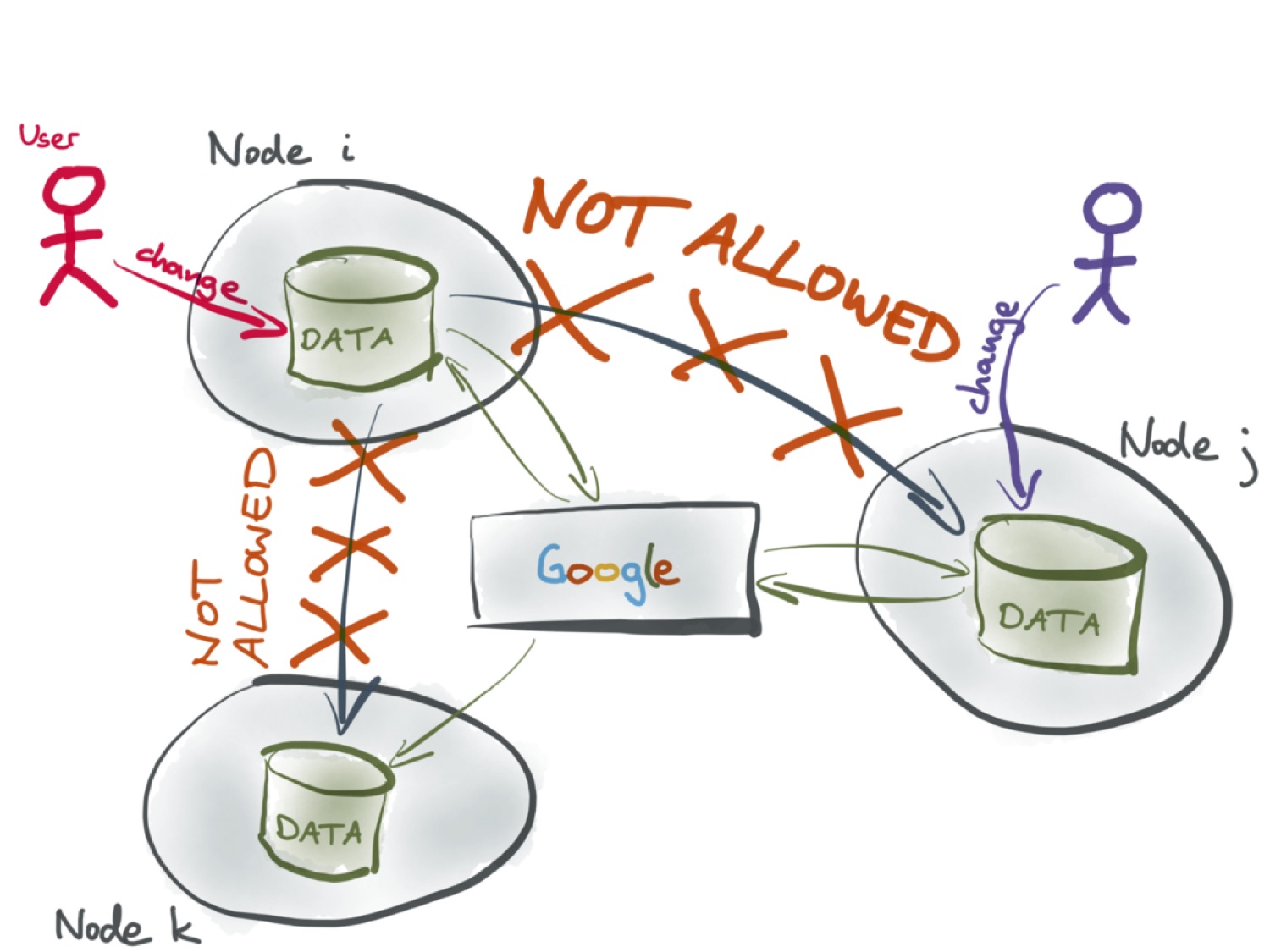
В алгоритмах CRDT не делается подобных предположений о топологии сети. Для них не требуется, чтобы вся связь шла через единый центр. Как следствие, такие алгоритмы более надёжные, и они работают для большего числа систем. Многие приложения, которые нельзя было реализовать с операциональным преобразованием, оказываются возможными с CRDT.
Сходимость
Алгоритмы CRDT и операционального преобразования гарантируют сходимость. Это означает, что если два пользователя видели один и тот же набор операций, то их документы должны быть в одном состоянии, даже если они получили эти операции в разном порядке. Это обязательное требование для согласованности; если оно не выполнено, версии пользователей не окажутся согласованы.
Но одной только сходимости недостаточно. Она лишь гарантирует, что состояние у пользователей одинаковое, но каким именно будет это состояние — неизвестно. Ниже мы с вами рассмотрим несколько примеров, когда состояние у пользователей одинаковое, причем одинаково неправильное.
Помимо сходимости, нужны способы убедиться, что наше итоговое состояние — именно то, которое нужно. Определить их бывает непросто, поскольку они зависят от нашего интуитивного представления о том, что именно будет желаемым результатом, а что — нет. Мы ещё увидим это на примерах. В общем, поработав несколько лет с CRDT, я пришёл к выводу, что базовую реализацию такого алгоритма сделать легко, но наломать дров в реализации — ещё проще. Мы с вами рассмотрим способы обойти эти проблемы и реализовать CRDT лучше привычных подходов.
Хочу привести четыре примера конкретных проблем. Первый:
Аномалии чередования в текстовых редакторах для совместной работы
Речь идёт о ситуации, когда несколько пользователей пытаются одновременно вставить текст на одной и той же позиции документа.
Я уже говорил, что алгоритмы операционального преобразования используют индекс символа. Алгоритмы CRDT же индексами не пользуются; вместо этого они присваивают каждому символу документа уникальный идентификатор. Механизмы генерации таких идентификаторов используются разные. Часто это делают с помощью дробей. Предположим, каждый символ у нас представлен числом от 0 до 1, где 0 — начало документа, а 1 — окончание. В примере с документом «Helo» позицию первого символа будет представлять число 0.2, второго — 0.4, третьего — 0.6, четвёртого — 0.8.
Тогда при добавлении второй буквы «l» между первой «l» и «o» этому новому символу будет присвоено значение от 0.6 до 0.8 — например, 0.7. Подобным же образом восклицательному знаку присваивается значение 0.9.
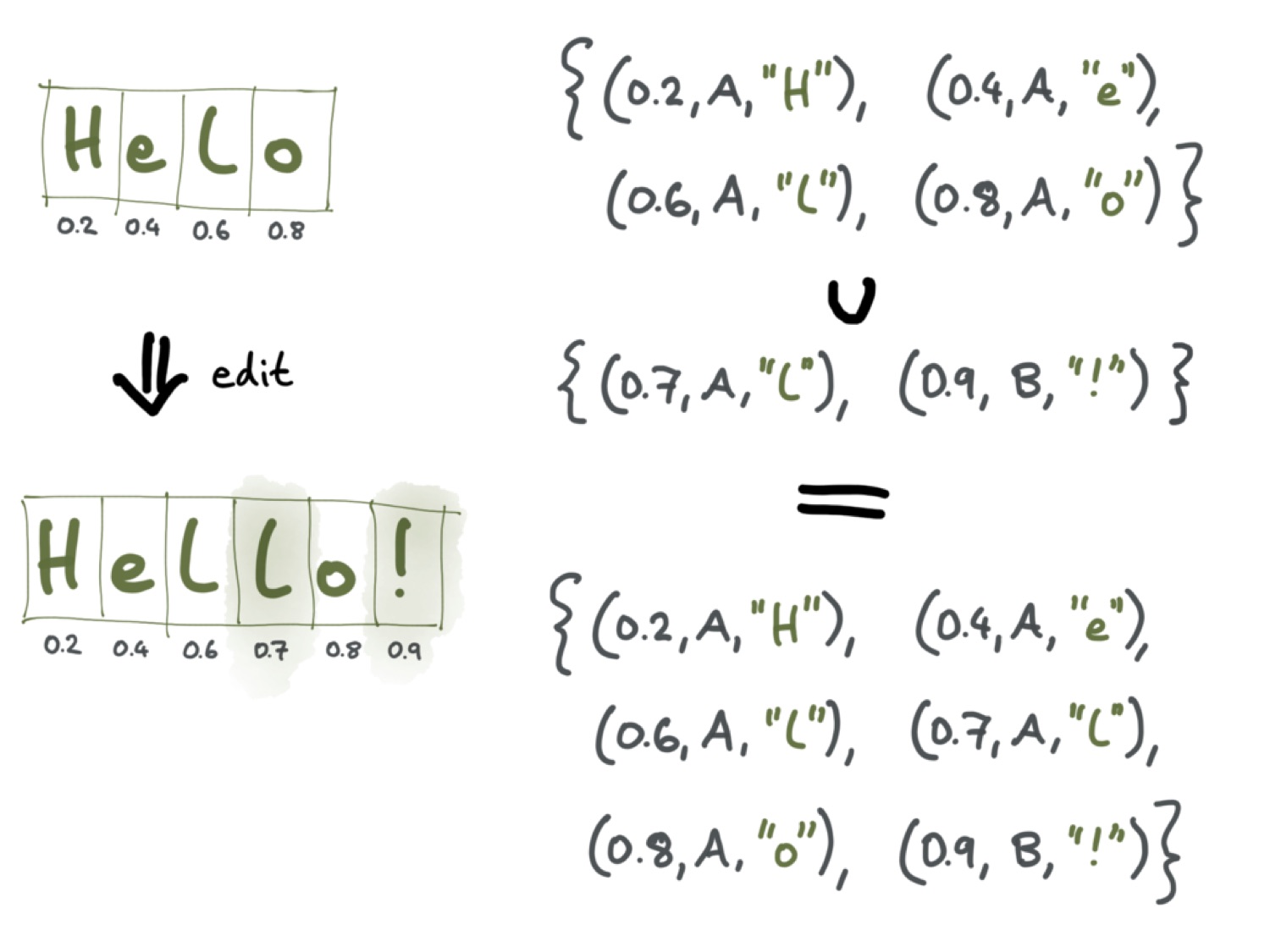
Состояние такой структуры данных можно представить как множество кортежей. Первому тексту соответствует множество кортежей, в котором каждому символу присвоено число, определяющее положение этого символа в тексте, а также идентификатор узла или пользователя, добавившего этот символ. Такой идентификатор необходим, потому что если два пользователя параллельно добавляют символы на одной и той же позиции в тексте, этим символам могут быть присвоены одинаковые числа. Тогда порядок символов уже не является однозначным. Такие конфликты между одинаковыми числами у разных символов можно разрешать на основе идентификаторов пользователя, создавшего символ.
При таком подходе, чтобы получить итоговый документ, необходимо просто выполнить объединение множеств кортежей, а затем упорядочить символы в порядке возрастания соответствующих им чисел.
Звучит разумно. К сожалению, у этого подхода есть существенный недостаток. Рассмотрим пример на слайде.
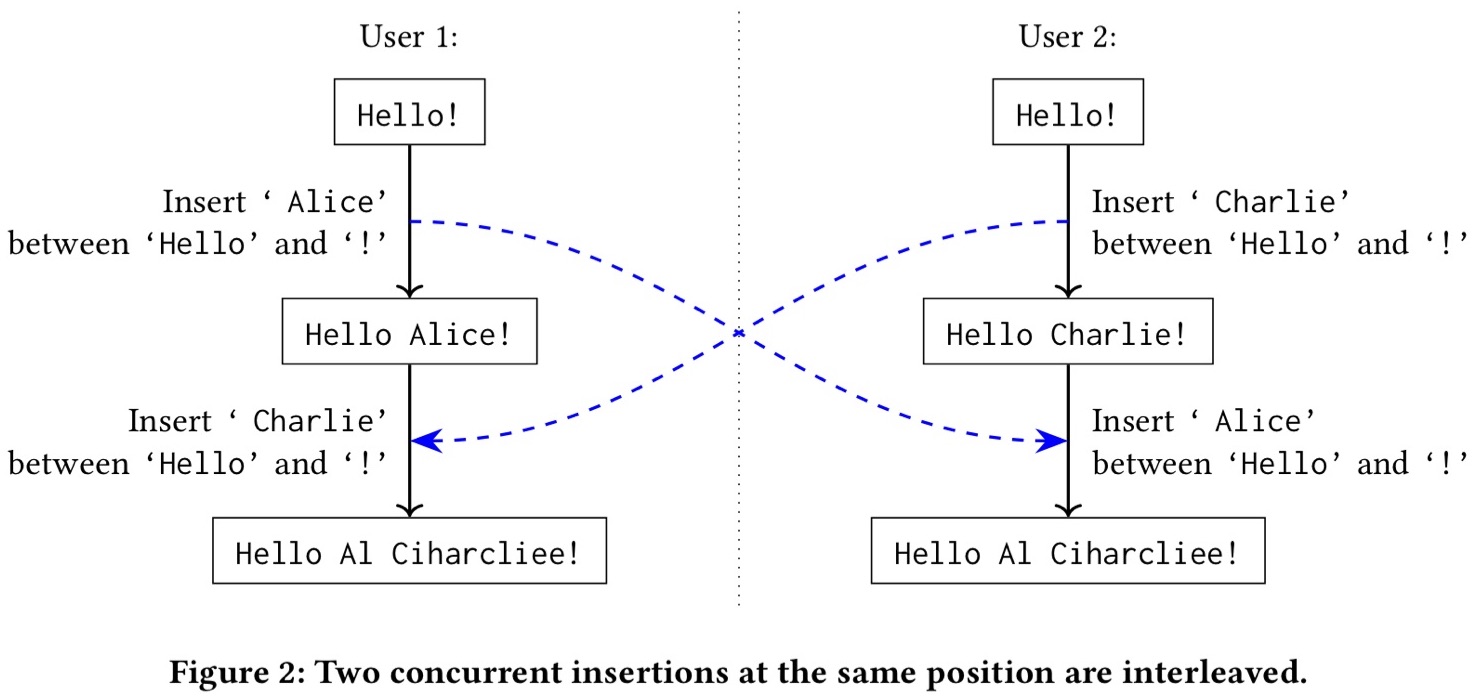
У нас есть документ «Hello!». Один пользователь добавил « Alice» перед восклицательным знаком, второй пользователь добавил « Charlie». Но в результате слияния этих изменений мы получили нечто совершенно непонятное. Почему это произошло? Чтобы разобраться, взглянем на схему, представленную на следующем слайде.
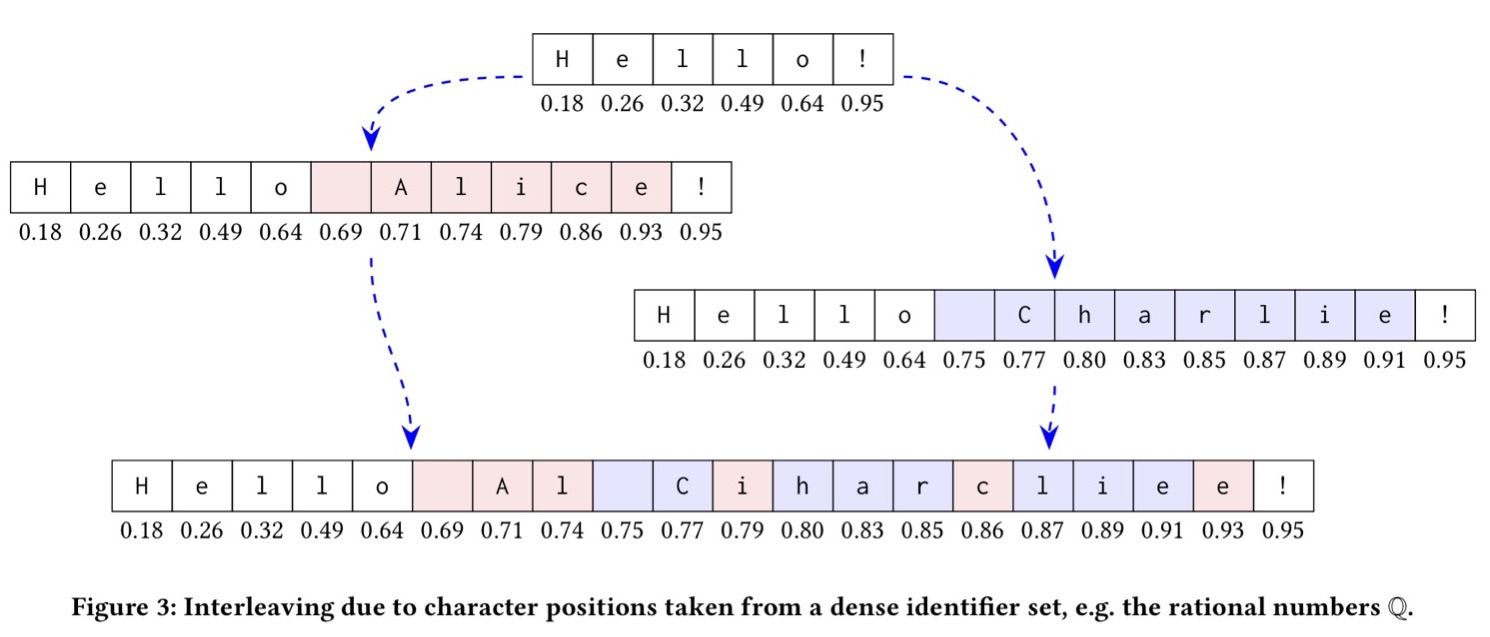
В первоначальном документе символу «o» соответствует цифра 0.64, а восклицательному знаку — 0.95. Первый пользователь добавил несколько символов между этими двумя, и новым символам были присвоены значения от 0.64 и до 0.95. Параллельно этому второй пользователь добавил свои символы на той же позиции, и им были присвоены цифры в том же диапазоне.
Какие именно цифры здесь используются, не так уж и важно. Алгоритмы, действующие по этому принципу, часто добавляют в код символа случайную составляющую, чтобы сделать максимально редкими ситуации, когда изменения разных пользователей получают один и тот же индекс. К сожалению, из-за этого при объединении множеств от разных пользователей для одной позиции мы получим чередование изменений от первого и от второго пользователя, то есть бессмысленный набор символов.
Заметьте, что в нашем примере каждый пользователь добавил только одно слово. При добавлении параграфов или целых разделов всё было бы ещё печальнее. А ведь на практике это вполне может произойти — например, если оба пользователя добавляют новый материал в конце документа или в начале раздела. Итоговый документ окажется нечитаемым, все изменения придётся переписывать. Понятно, что пользователям это не понравится.
Мы рассмотрели несколько существующих алгоритмов CRDT для текста на предмет чередования, результаты этого сравнения представлены на следующем слайде.

Проблему чередования мы нашли как минимум в двух алгоритмах — Logoot и LSEQ. Из-за особенностей этих алгоритмов простого способа решить эту проблему для них нет. Нам не удалось улучшить их в этом отношении, не изменив при этом фундаментально самих алгоритмов. В Treedoc и WOOT мы этой проблемы не нашли, но, к сожалению, эти алгоритмы наименее эффективные. Собственно говоря, главной причиной, по которой был создан LSEQ, было достижение большей производительности по сравнению с Treedoc и WOOT. Возвращаться к этим неэффективным алгоритмам не хотелось бы. Далее, Astrong — не алгоритм, а спецификация, формализующая требования к алгоритмам редактирования текста. К сожалению, она также допускает чередование.
RGA
Отдельный случай — алгоритм RGA. Непосредственно той проблемы, о которой я сейчас говорил, там нет, зато есть другая, правда, менее существенная. Попробуем вкратце её рассмотреть.
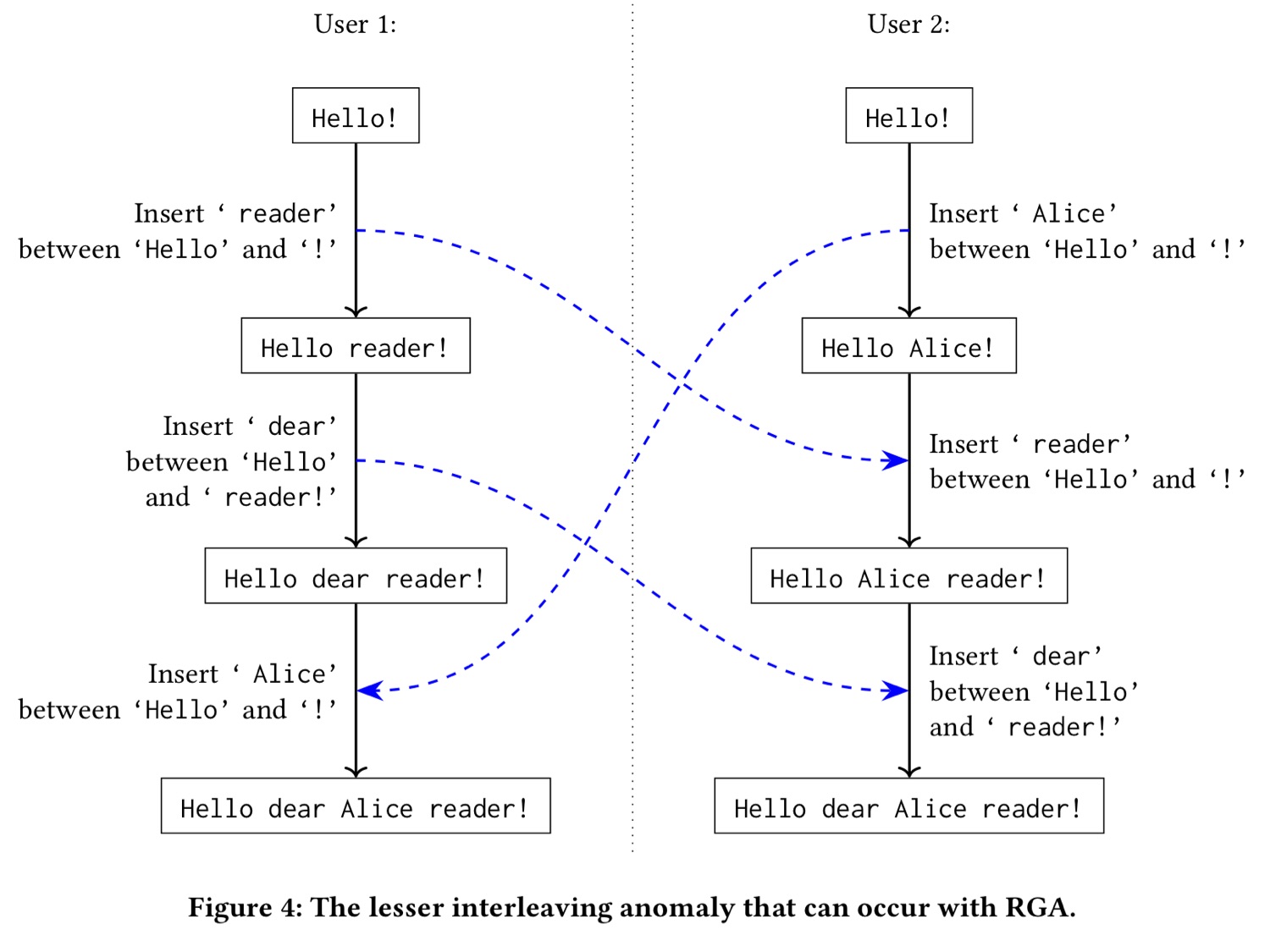
На слайде представлен пример, в котором один пользователь добавляет слово « reader» между «Hello» и «!», затем возвращает курсор к позиции непосредственно перед « reader» и добавляет « dear». Здесь очень важно именно перемещение курсора. Второй пользователь только добавляет « Alice» между «Hello» и «!». При действии алгоритма RGA возможным результатом этих операций будет чередование слов: «Hello dear Alice reader!». Это тоже нежелательно, хоть и лучше, чем чередование символов.
Давайте разберёмся, почему это происходит. RGA использует структуру, показанную на слайде.
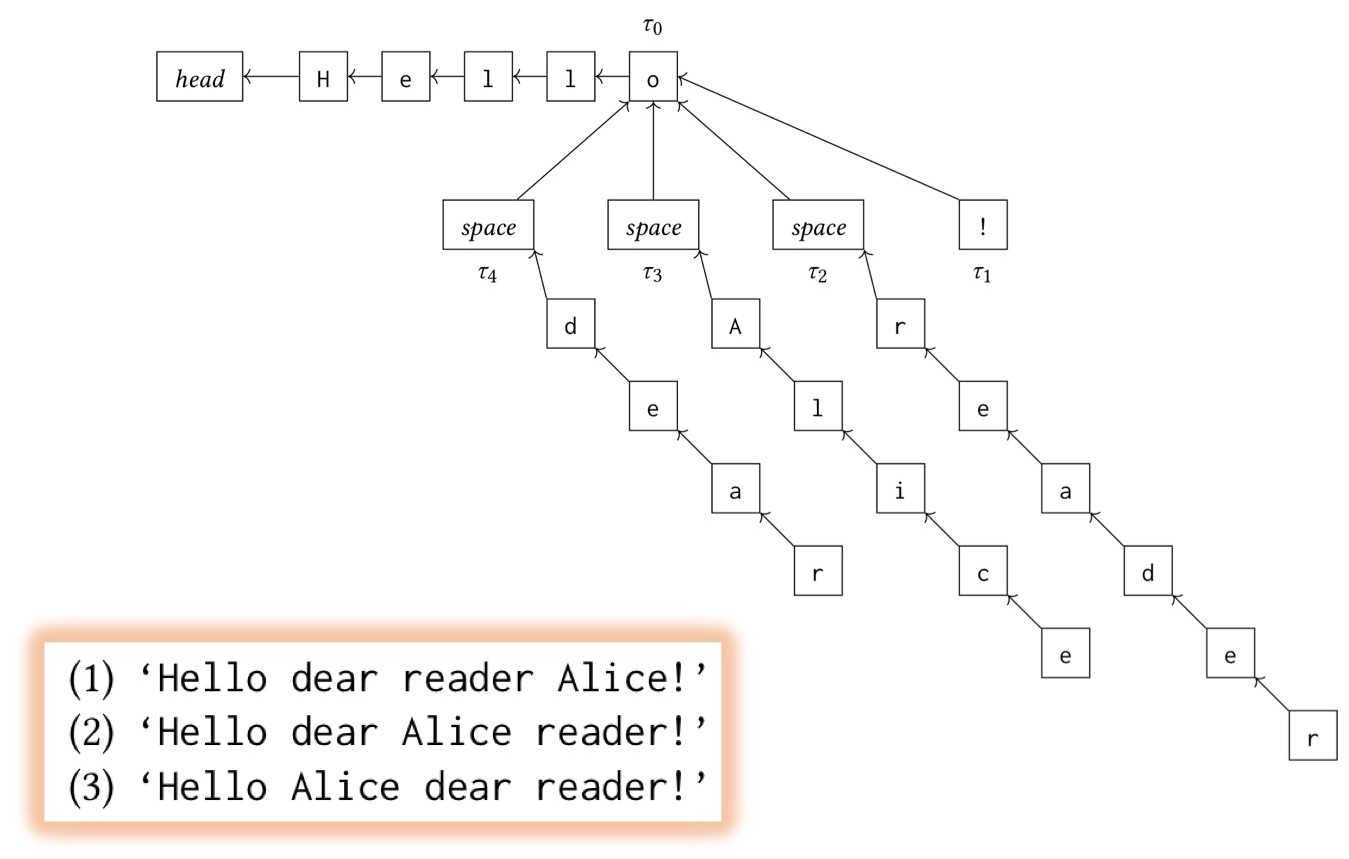
В ней текст представлен в виде очень глубокого дерева, в котором родителем каждого символа является предшествующий на момент добавления символ. Счёт идёт от положения курсора на момент ввода символа. Исходный текст — «Hello!». Затем у нас есть три случая перемещения курсора — перед написанием «reader», «Alice» и «dear». В такой ситуации алгоритм RDA генерирует один из трёх возможных результатов, перечисленных на слайде. Из них второй, на мой взгляд, является нежелательным, поскольку в нём происходит чередование слов разных пользователей. Другие два результата вполне допустимы.
Наихудший сценарий при алгоритме RGA — если пользователь напишет весь документ символ за символом от конца к началу. В этом случае возможно произвольное посимвольное чередование, поскольку перед каждым символом курсор перемещается в начало документа. Учитывая, что большинство пользователей пишут документы всё-таки от начала к концу и более-менее линейно, проблема чередования у RGA значительно менее серьёзная, чем у других алгоритмов. Поэтому в нашей работе мы предпочитаем RGA другим алгоритмам.
В Logoot и LSEQ проблема чередования, как мне кажется, нерешаема, и, к сожалению, использовать их из-за этого нельзя. Мы разработали алгоритм для RGA, который позволяет избавиться даже от этого варианта проблемы чередования, но сейчас у меня нет времени на нём останавливаться. При желании с ним можно ознакомиться в нашей статье об аномалиях чередования, представленной на семинаре PaPoC в 2019 году. Там подробно описан этот алгоритм.
Перемещение элементов в списке
Мы опубликовали статью на эту тему всего несколько месяцев назад (PaPoC 2020). На слайде проблема представлена на примере списка задач.
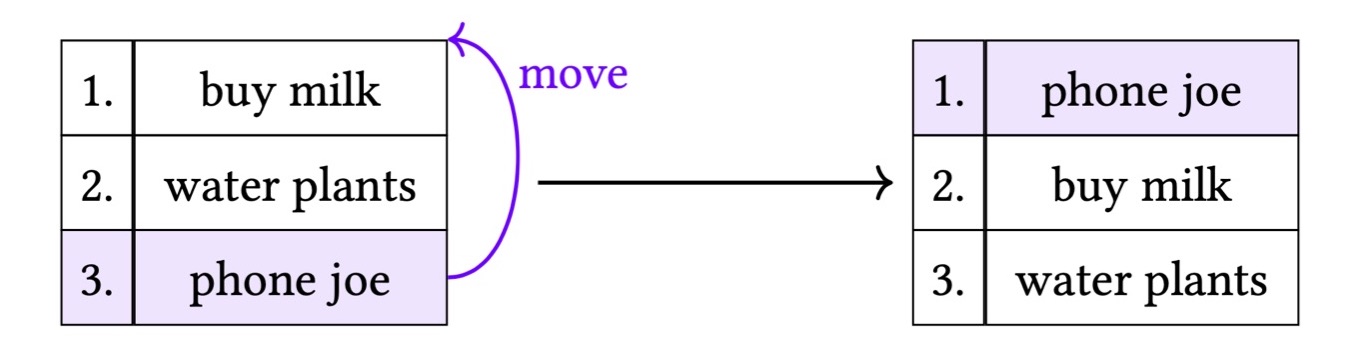
При составлении списков задач пользователям часто бывает необходимо изменить порядок элементов. В нашем случае пользователь вначале написал, что ему нужно купить молоко, полить цветы и позвонить Джо, а потом решил, что позвонить Джо нужно в первую очередь, и переместил этот элемент в начало списка.
Такую структуру данных можно представить с помощью CRDT-списка. В сущности, это то же самое, что CRDT для редактирования текста. Ни в одном из имеющихся алгоритмов CRDT нет встроенной операции перемещения элемента в списке. Вместо неё есть операции удаления элемента и добавления элемента. Казалось бы, операцию перемещения легко представить как операцию удаления с последующей операцией добавления на необходимой позиции в списке.
Давайте посмотрим, что произойдёт при таком подходе в ситуации, когда два пользователя осуществляют перемещение параллельно — как это происходит на слайде.
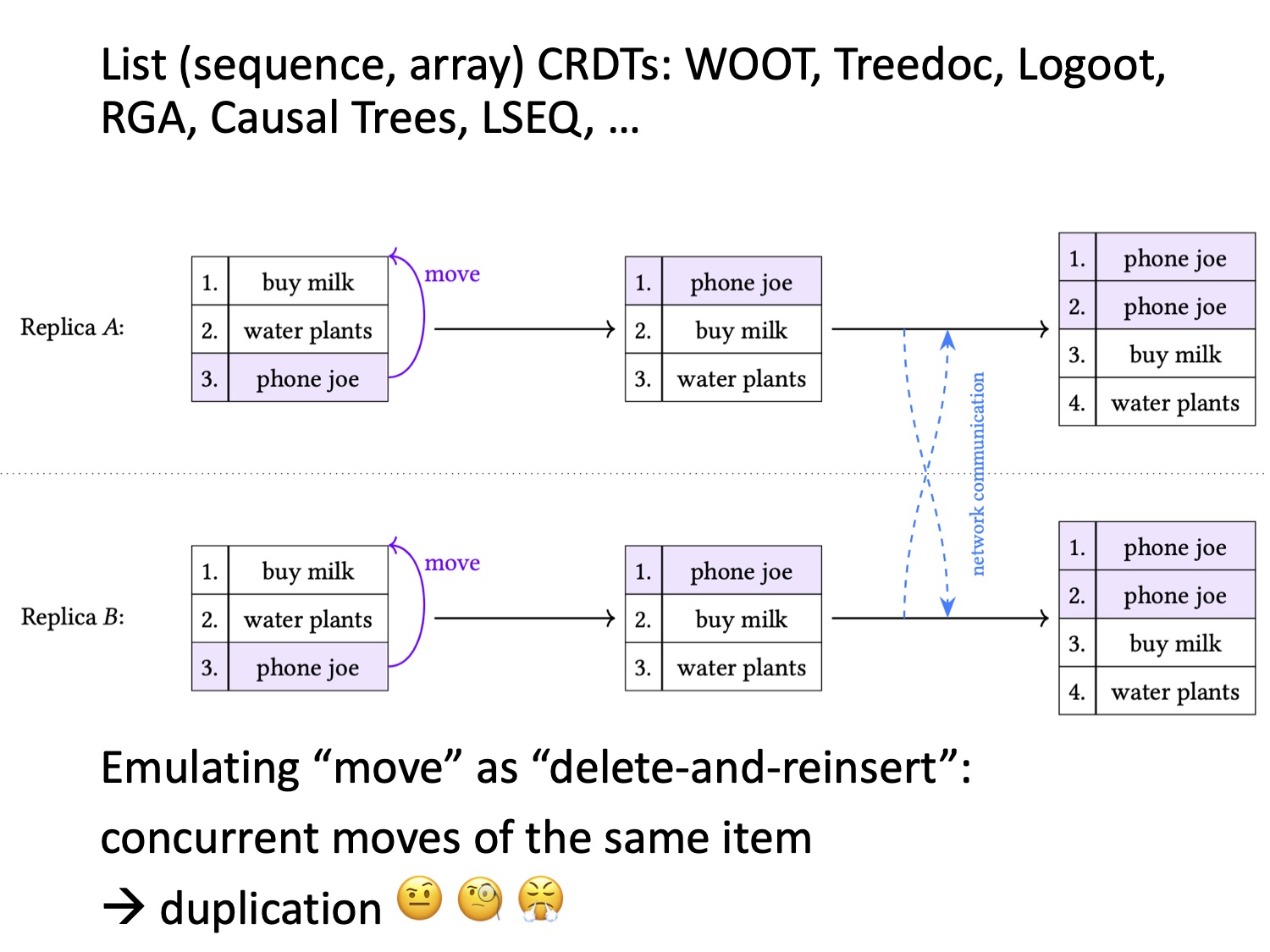
Оба пользователя одновременно выполняют одну и ту же операцию: перемещают операцию «phone joe» с последней позиции в списке на первую. Операция перемещения реализована как удаление с последующим добавлением, поэтому вначале необходимый элемент дважды удаляется на старой позиции. Здесь разницы с тем, чтобы удалить его один раз, нет. А вот если добавить элемент дважды, то на новой позиции появится два элемента «phone joe» вместо одного. Ясно, что такой вариант нам не подходит.
Давайте спросим себя: что именно должно было произойти в этой ситуации?
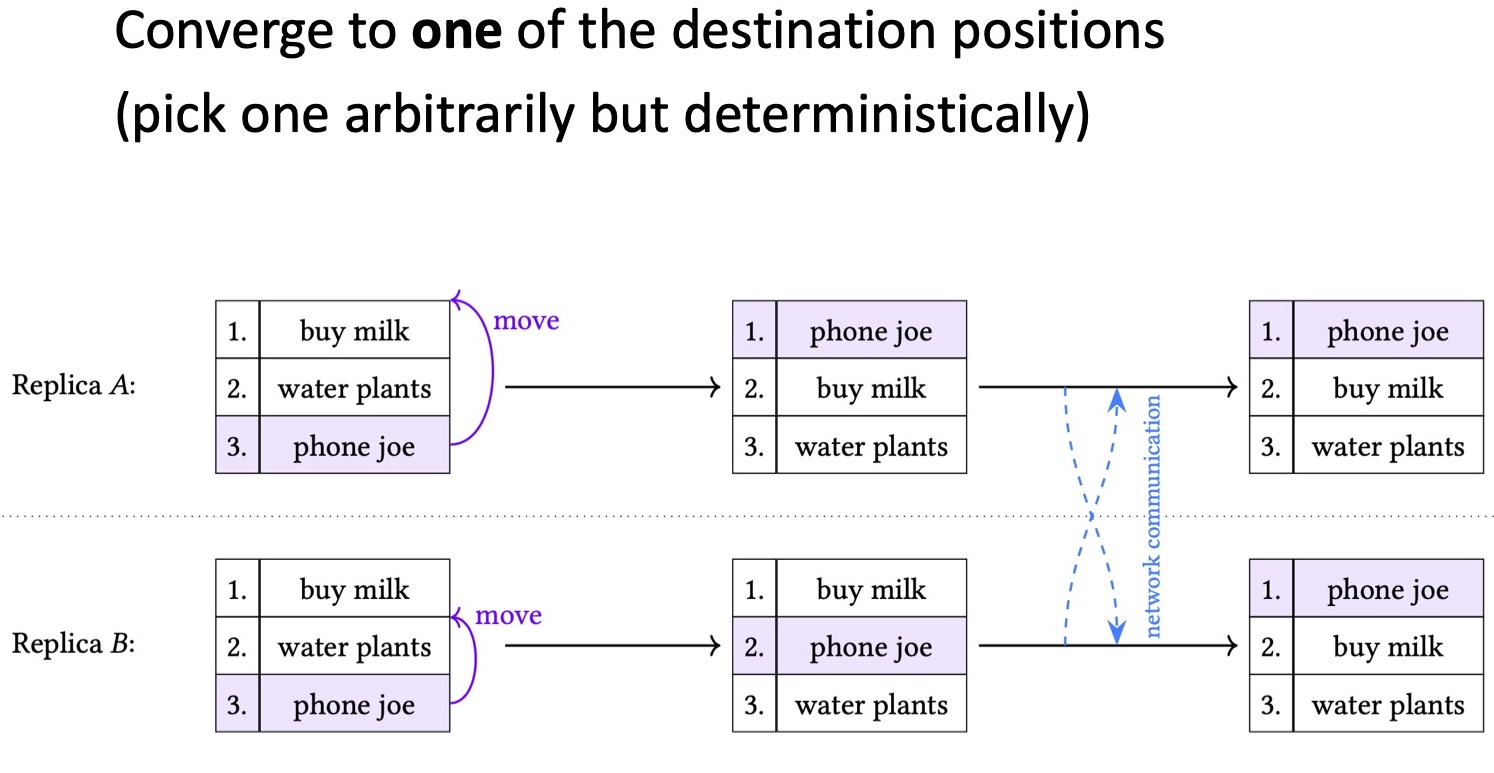
На слайде представлен другой пример, в котором всё тот же элемент пользователи переместили на разные итоговые позиции в списке. Первый пользователь переместил элемент «phone joe» в начало списка, второй — на позицию после «buy milk». К какому именно результату должен прийти алгоритм? Он может, как и в прошлом примере, дублировать элемент «phone joe», чтобы в итоге этот элемент оказался и в начале списка, и после «buy milk». Но это нежелательный вариант. Перемещаемый элемент должен оказаться лишь на одной из этих двух позиций. Чтобы этого достичь, необходимо выбрать одну из двух конфликтующих версий, причём выбрать произвольно, но детерминистично. В нашем примере выбрана версия, в которой «phone joe» оказывается в начале списка.
Как реализовать такой вариант? Если вы знакомы с существующими работами в области CRDT, это может выглядеть знакомо. Мы тут смотрим на ситуацию, в которой произвольно, но детерминистически выбираем одно из нескольких параллельно записываемых значений. Такое происходит к last writer wins register. Там, если значение могут обновлять несколько пользователей, при параллельной записи нескольких значений выбирается одно на основе произвольного критерия вроде метки времени.
Дальше это значение становится общим, а остальные значения удаляются. В нашем примере со списком необходимо именно такое поведение. Мы можем представить позицию каждого элемента в списке как last writer wins register, а значение, находящееся в регистре — как описание позиции данного элемента. Когда первый пользователь указывает для позиции «phone joe» начало списка, а второй перемещает этот элемент на позицию после «buy milk», нам необходимо, чтобы одно из этих значений стало общим для обоих пользователей. Таким итоговым значением может быть начало списка.
То есть для операции перемещения мы можем использовать существующий CRDT (last writer wins register). Чтобы реализовать такую операцию, необходимы две вещи. Во-первых, сам регистр, и, во-вторых, способ описать положение некоторого элемента в списке (это и будет значением, содержащимся в регистре). Но если подумать, то такой способ уже есть.
Вспомните, что я уже говорил выше. Все CRDT присваивают каждому элементу списка или символу в тексте уникальный идентификатор. Каким именно будет этот идентификатор, зависит от того, какой используется алгоритм CRDT. Например, в Treedoc применяется путь через бинарное дерево, в Logoot — путь через более сложное дерево с большим фактором ветвления, в RGA — метка времени и так далее. Во всех этих CRDT есть работающий механизм обращения к определённой позиции в списке. Так что позиции можно сгенерировать с помощью существующих алгоритмов. А при перемещении элемента на новую позицию можно создать новый идентификатор для позиции, на которую мы хотим переместить элемент, после чего записать этот идентификатор в наш last writer wins register.
Помимо этого, нам необходим отдельный регистр last writer wins для каждого элемента в списке. Но здесь тоже есть простое решение: это набор CRDT add-wins set (AWSet на слайде):
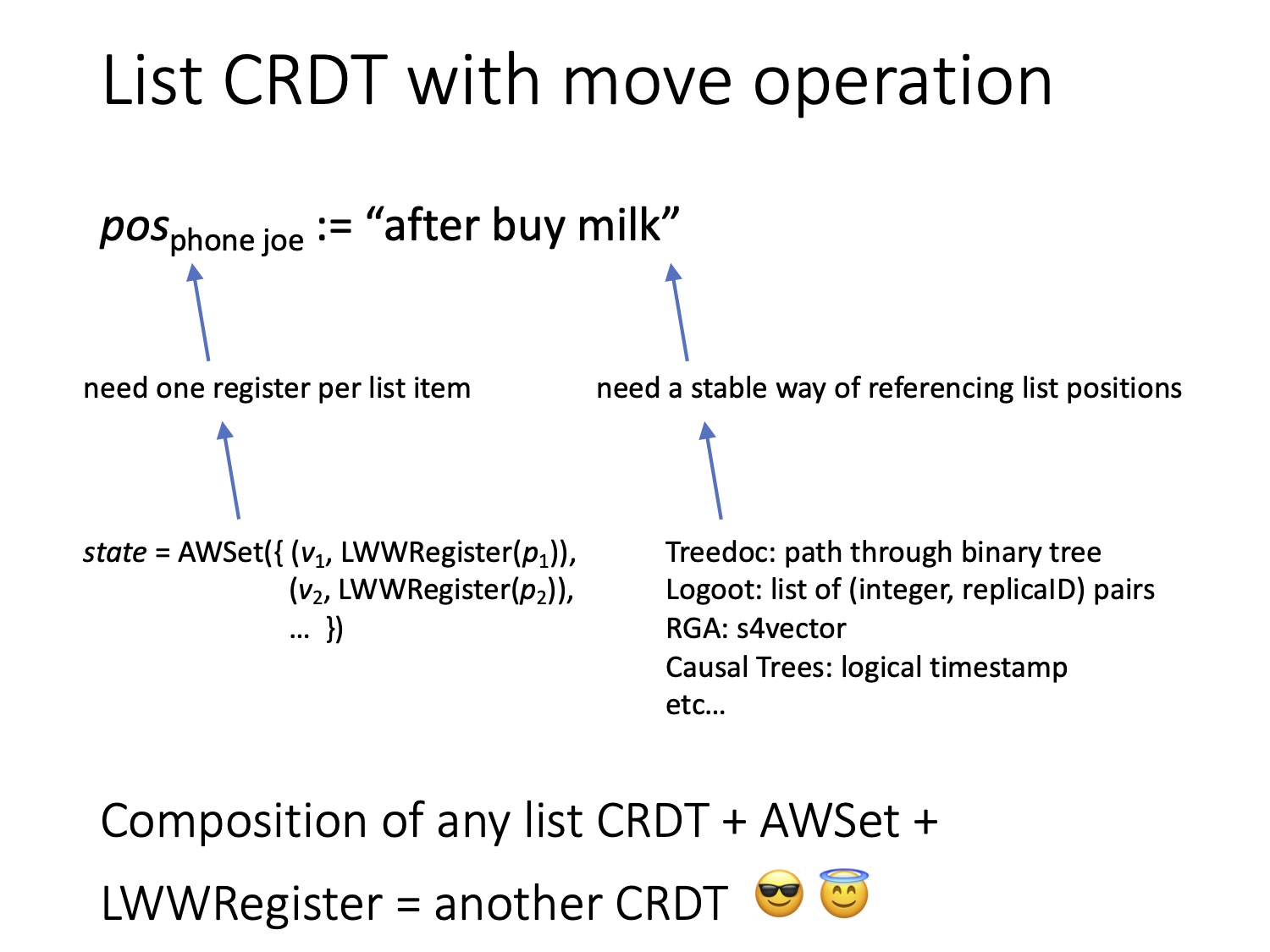
Можно создать add-wins set, в котором каждый элемент набора является пунктом нашего списка и состоит из пары, а именно, значения элемента (например, описание пункта списка) и регистра last writer wins с положением этого пункта. Регистр last writer wins можно поместить в набор AWSet, а идентификаторы позиции из CRDT списка можно поместить в регистр last writer wins register. Итак, мы объединили три CRDT и создали новый CRDT, а именно CRDT списка с операцией перемещения. Он позволяет атомарно переместить элемент с одной позиции в списке на другую — что, согласитесь, весьма неплохо. Заметьте, что этот подход работает с любым из существующих алгоритмов CRDT списка. То есть любой существующий CRDT можно дополнить операцией перемещения.
До сих пор мы рассматривали только перемещение отдельных элементов в списке. В списке задач перемещать несколько задач одновременно, как правило, не нужно, в крайнем случае их нетрудно переместить по одной. Но при редактировании текста нужна более общая операция перемещения, которая может работать с последовательностями символов. Давайте попробуем представить список в качестве текста. Здесь каждый элемент списка начинается с символа маркера и заканчивается символом новой строки:
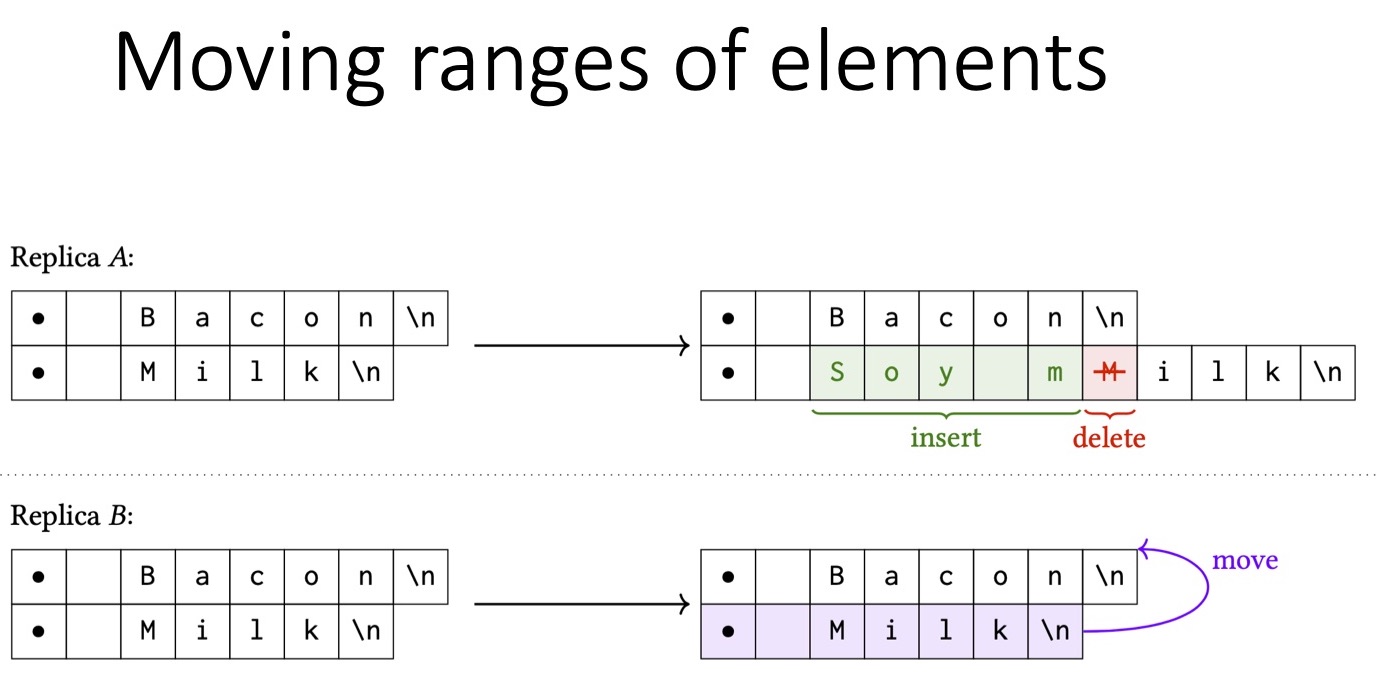
Предположим, второй пользователь хочет переместить элемент «Milk» со второго места в списке на первое, то есть одновременно переместить последовательность символов. Параллельно этому первый пользователь изменяет «Milk» на «Soy milk». Для этого он вначале удаляет первый символ слова «Milk», а затем добавляет все остальные символы. В итоге возникло два отличающихся документа, которые теперь необходимо привести к одному состоянию. Каким должно быть это состояние? Интуитивно ожидаемый вариант — переместить «Milk» в начало списка и изменить текст на «Soy milk». К сожалению, если мы применим описанную мной выше операцию перемещения, то получим результат, показанный на следующем слайде.
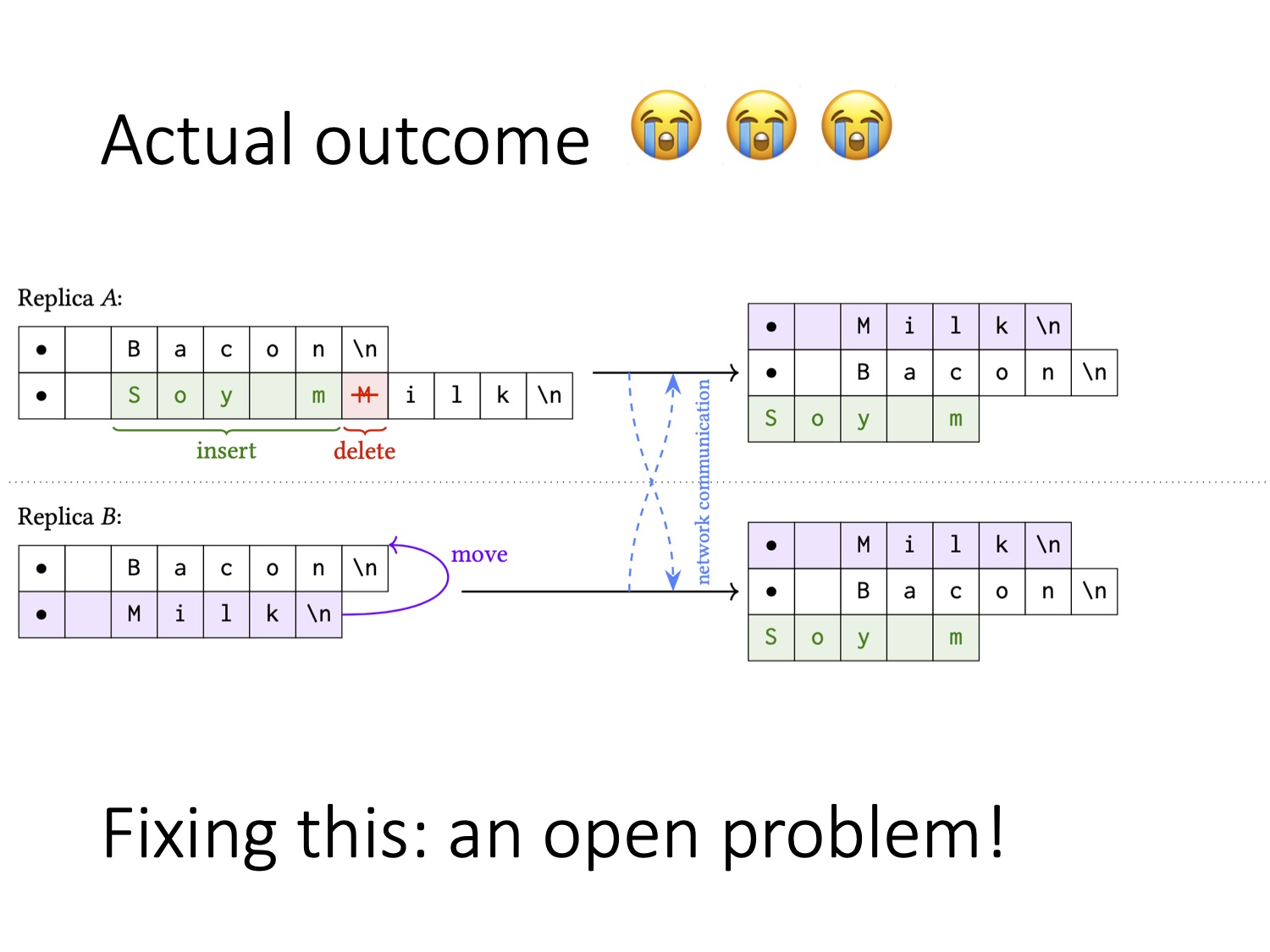
Не знаю как вам, а мне на него смотреть грустно. Элемент «Milk» был перенесён на первую позицию в списке, но все изменения в этом элементе остались на старой позиции этого элемента. В результате документ заканчивается символами «Soy m». Это произошло потому, что позиция, на которой было выполнено добавление этих символов, не изменилась. Я не думаю, что эта проблема нерешаемая, но пока что нам не удалось найти адекватного способа её преодолеть. Я буду очень рад, если кто-то из вас захочет над ней подумать.
Перемещение деревьев
Вообще деревья — крайне полезная структура данных. Файловая система вашего компьютера, документ JSON или XML — всё это примеры деревьев. Предположим, у вас есть приложение, которое использует то или иное дерево — например, распределённую файловую систему или документ JSON с возможностью перемещать поддерева документа. Такому приложению необходима операция перемещения. И здесь сразу возникает проблема, целиком аналогичной той, с которой мы уже встречались в контексте списков: что происходит, когда несколько пользователей параллельно перемещают один и тот же узел на разные позиции?
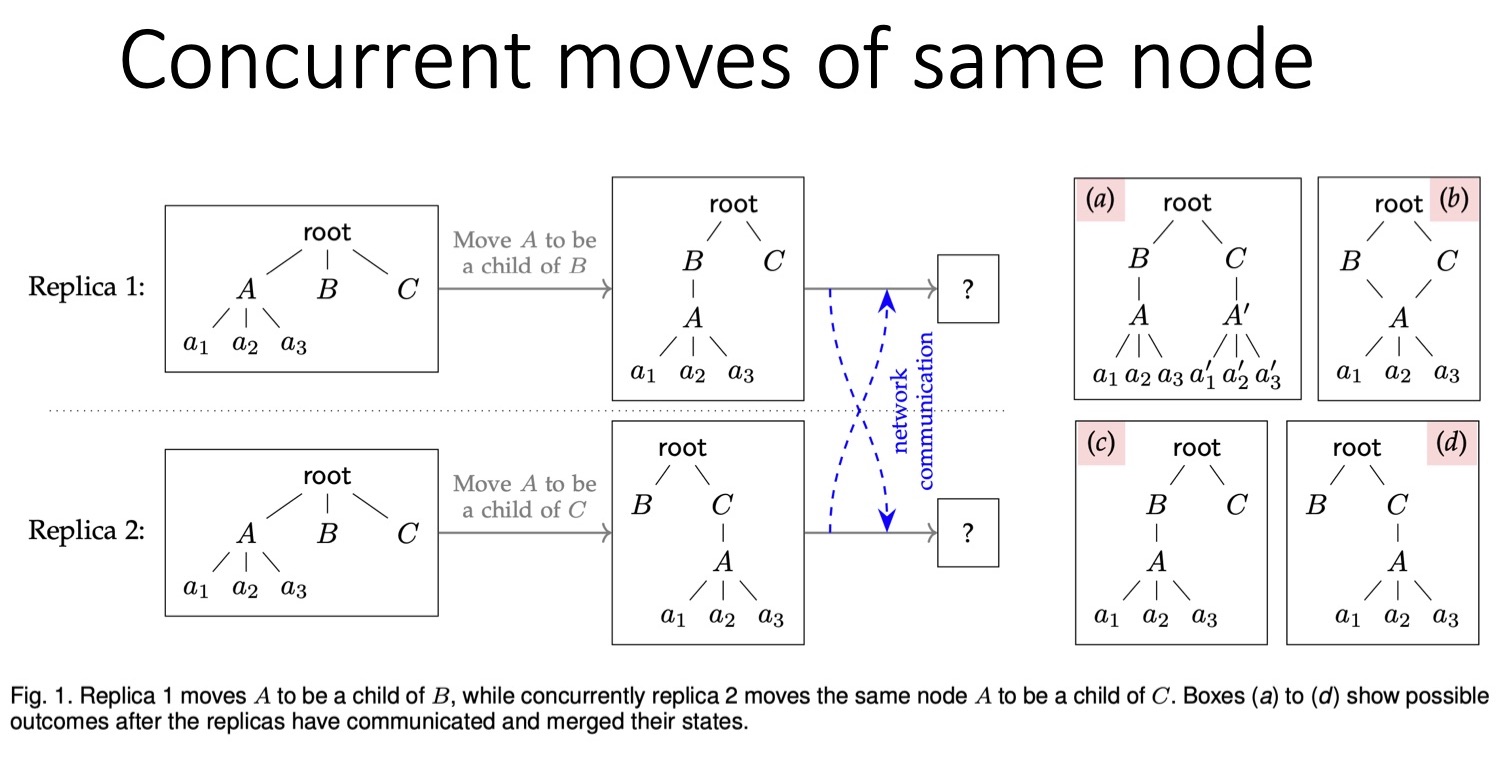
В примере на слайде первый пользователь перемещает узел А (со всеми дочерними узлами) так, что тот становится дочерним узлом B. Одновременно второй пользователь делает узел А дочерним узлом C. При таком конфликте возможны четыре итоговых дерева, которые представлены в правой части слайда. Во-первых, узел А может быть дублирован — это не лучшее решение проблемы. В новом дереве один узел А окажется дочерним для B, а другой — для C. Но помимо самого узла A нужно также скопировать все его дочерние узлы. В большинстве приложений такой итог нежелателен.
Второй вариант — сделать узел A одновременно дочерним и для B, и для C. Такая структура данных — уже не дерево, а ориентированный ациклический граф (DAG), или граф более общего типа. На мой взгляд, этот вариант тоже неудачный. Следует выбирать между третьим и четвёртым вариантами, где A является либо дочерним для B, либо дочерним для C. Здесь, как и в ситуации с перемещением в списке, одна версия становится общей, а вторая удаляется.
Но сейчас перед нами встаёт дополнительное затруднение. Вы можете поставить эксперимент у себя на компьютере. Создайте каталог «a», затем в нём создайте другой каталог «b», а потом попробуйте переместить «a» в «b». То есть попробуйте сделать «a» подкаталогом самого себя. Как вы думаете, что произойдёт? По идее, в результате должен возникнуть цикл. Я попробовал в macOS и получил сообщение об ошибке «Invalid argument». Подозреваю, что большинство операционных систем, в которых файловая система является деревом, реагируют подобным образом, потому что если разрешить такую операцию, то система уже не будет деревом.
Но обнаружить ситуацию, когда пользователь пытается сделать директорию дочерней для себя самой, довольно просто. А вот в случае с CRDT всё сложнее. Взглянем на пример на слайде.
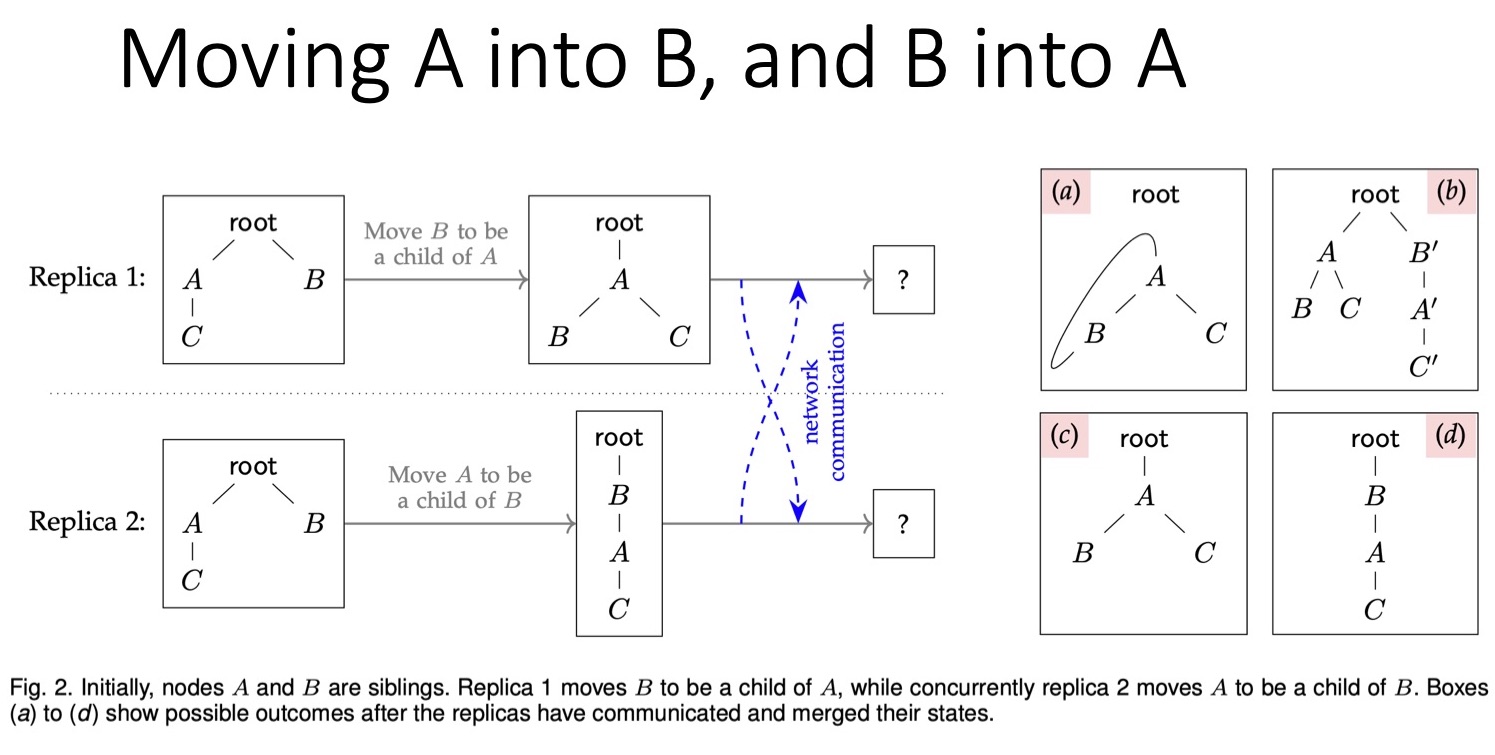
Первый пользователь сделал узел B дочерним для A. Второй пользователь одновременно с этим сделал узел A дочерним для B. По отдельности эти операции вполне допустимы и безопасны. Но если их выполнить одновременно, возникнет только что описанная проблема циклических связей. Возможные результаты таких операций представлены в правой части слайда.
Первый вариант содержит циклические связи, то есть эта структура данных уже не дерево. Второй вариант решения — дублирование. Можно скопировать A и B, так, чтобы в одном случае один узел являлся дочерним, а во втором — другой. Формально это допустимый вариант, но всё-таки нежелательный. Я полагаю, что здесь, как и в прошлом примере, нам следует выбрать одну из конфликтующих операций и удалить вторую. То есть либо A должна быть родителем B, либо наоборот, но не то и другое одновременно.
А как ведут себя существующие программы в таком случае? Я поставил эксперимент с Google Drive, результат которого виден на слайде.
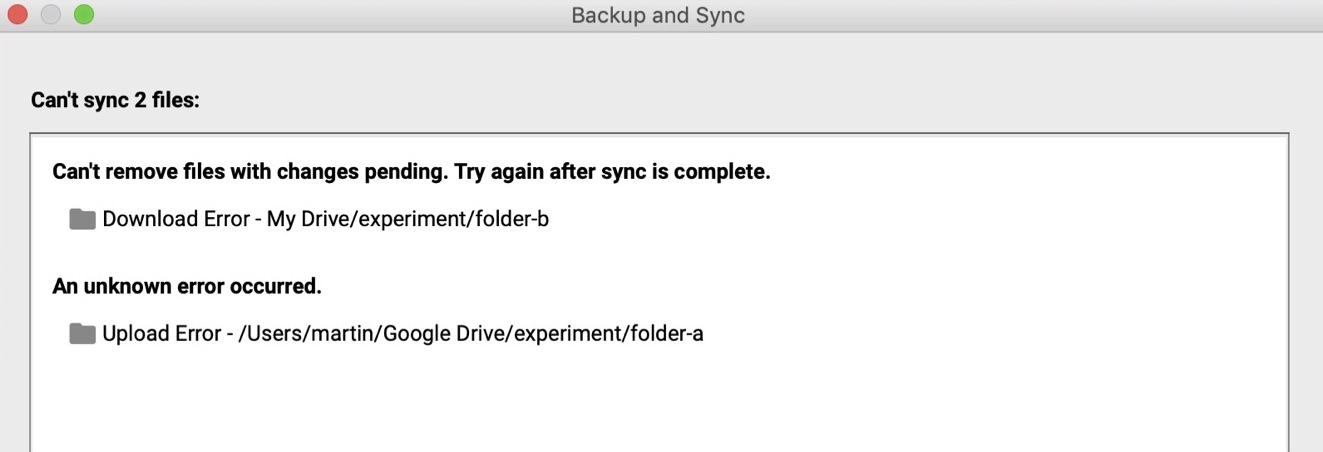
На одном компьютере я переместил A в B, на другом — B в A, затем дал им синхронизироваться. Google Drive вернул сообщение о неизвестной ошибке. Так что как видим, даже Google не удалось найти удовлетворительное решение этой проблемы. Но для CRDT правильное решение всё-таки необходимо. С этой целью мы разработали алгоритм, который позволяет безопасно выполнять такого рода операции для деревьев, не приводя к возникновению циклических связей. О нём я сейчас и расскажу.
Схематично этот алгоритм представлен на следующем слайде:
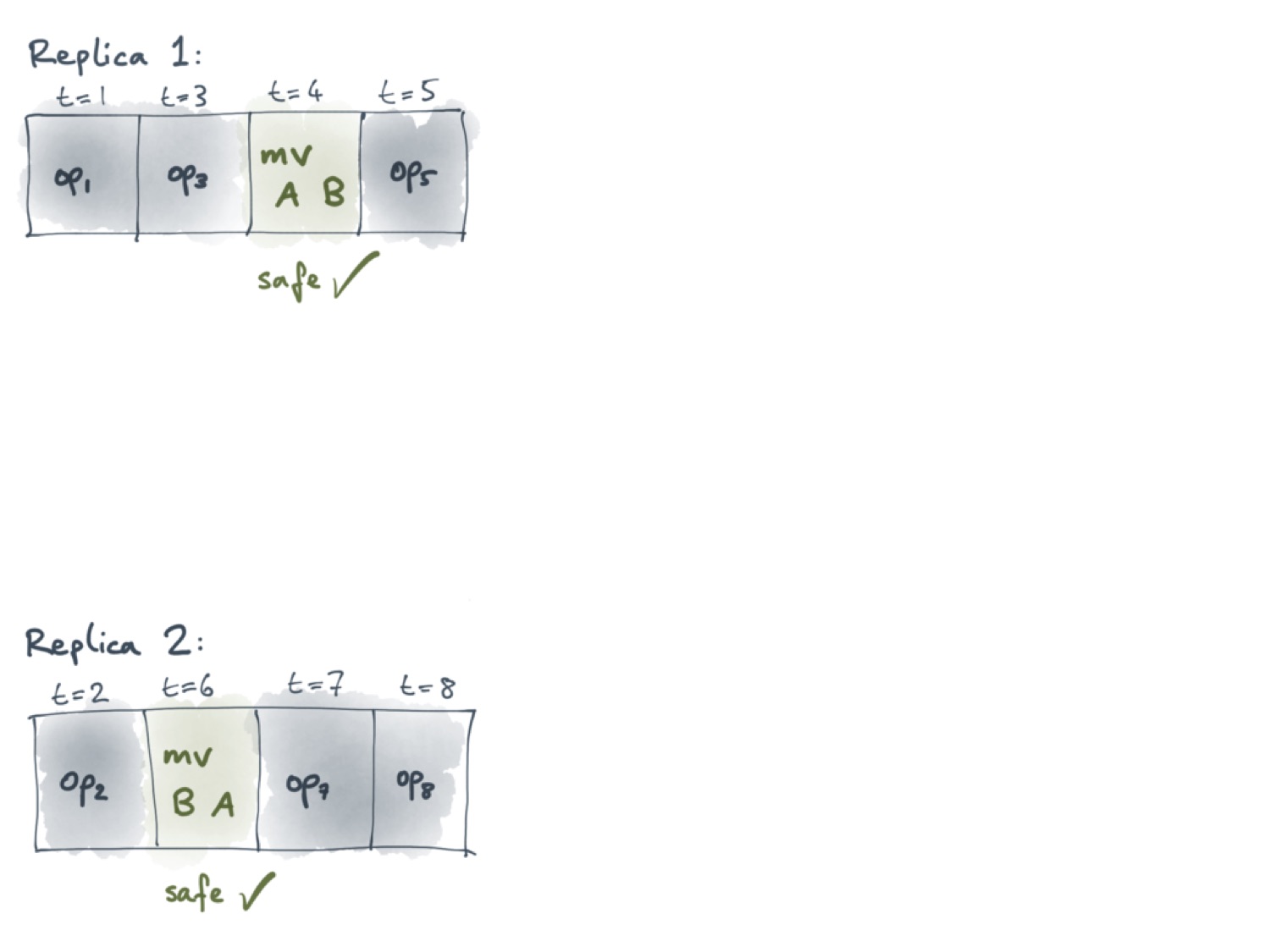
Первый пользователь здесь выполнил операции op1, op3, mv A B и op5. Каждой операции присвоена метка времени t. Для соответствующих операций значения этих меток — 1, 3, 4 и 5. У второго пользователя есть операция mv B A с меткой времени 6. Как уже говорилось, сами по себе эти операции перемещения безопасны. Сложности начинаются, когда мы пытаемся синхронизировать эти операции, как это показано на следующем слайде.
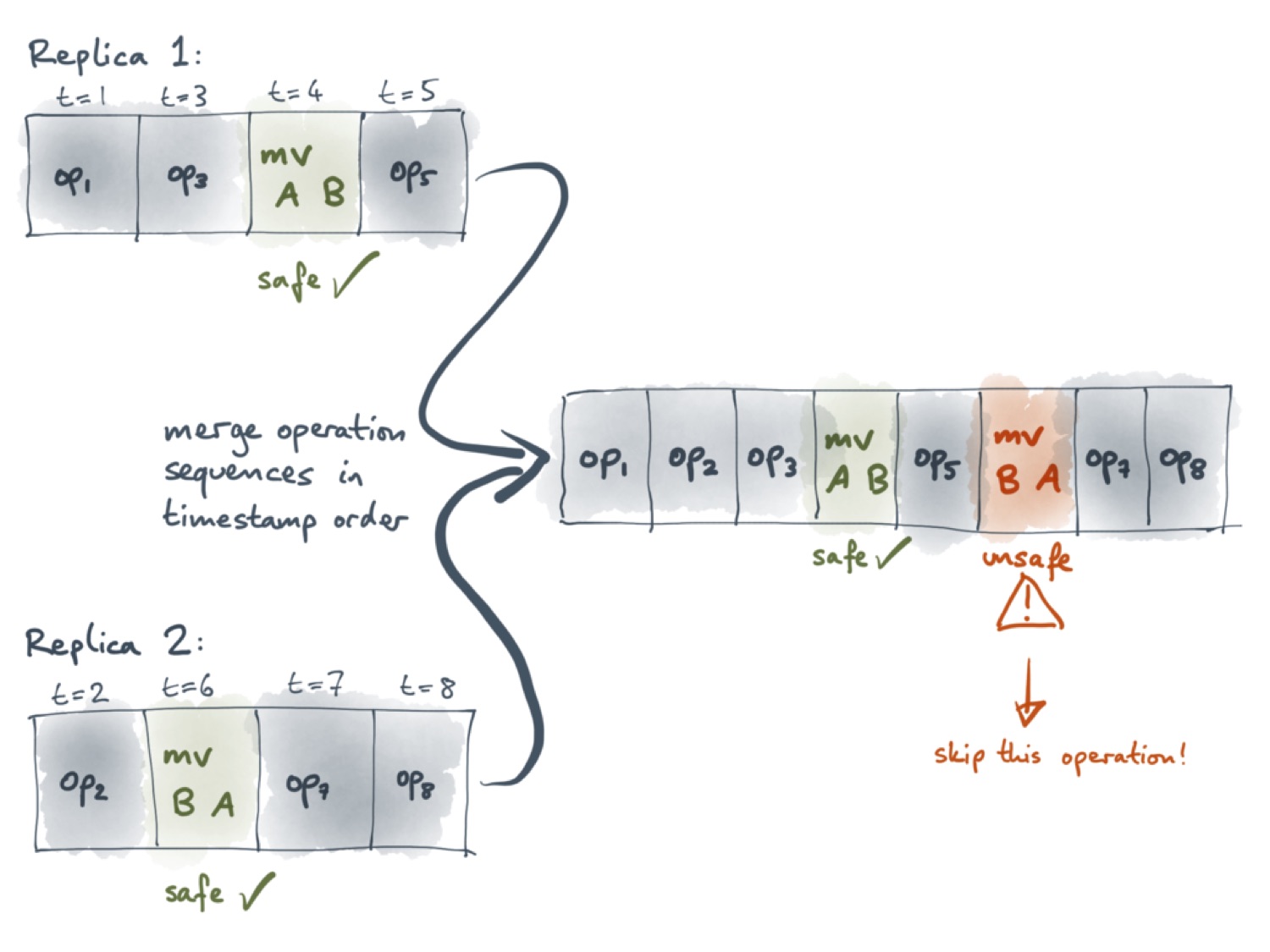
Самый простой способ выполнить синхронизацию — это объединить все операции в один список, расположив их в порядке возрастания метки времени. В этом случае первая операция перемещения всё ещё безопасная, а вторая уже может вызвать цикл. Поэтому нам необходим способ пропустить эту операцию.
Давайте взглянем теперь на ситуацию с точки зрения первого пользователя. В его версии уже выполнены операции с метками времени от 1 до 5. С ними теперь нужно синхронизировать операцию op2, выполненную вторым пользователем. Поскольку значение её метки времени — 2, она должна оказаться между двумя операциями первого пользователя, как это показано на следующем слайде.
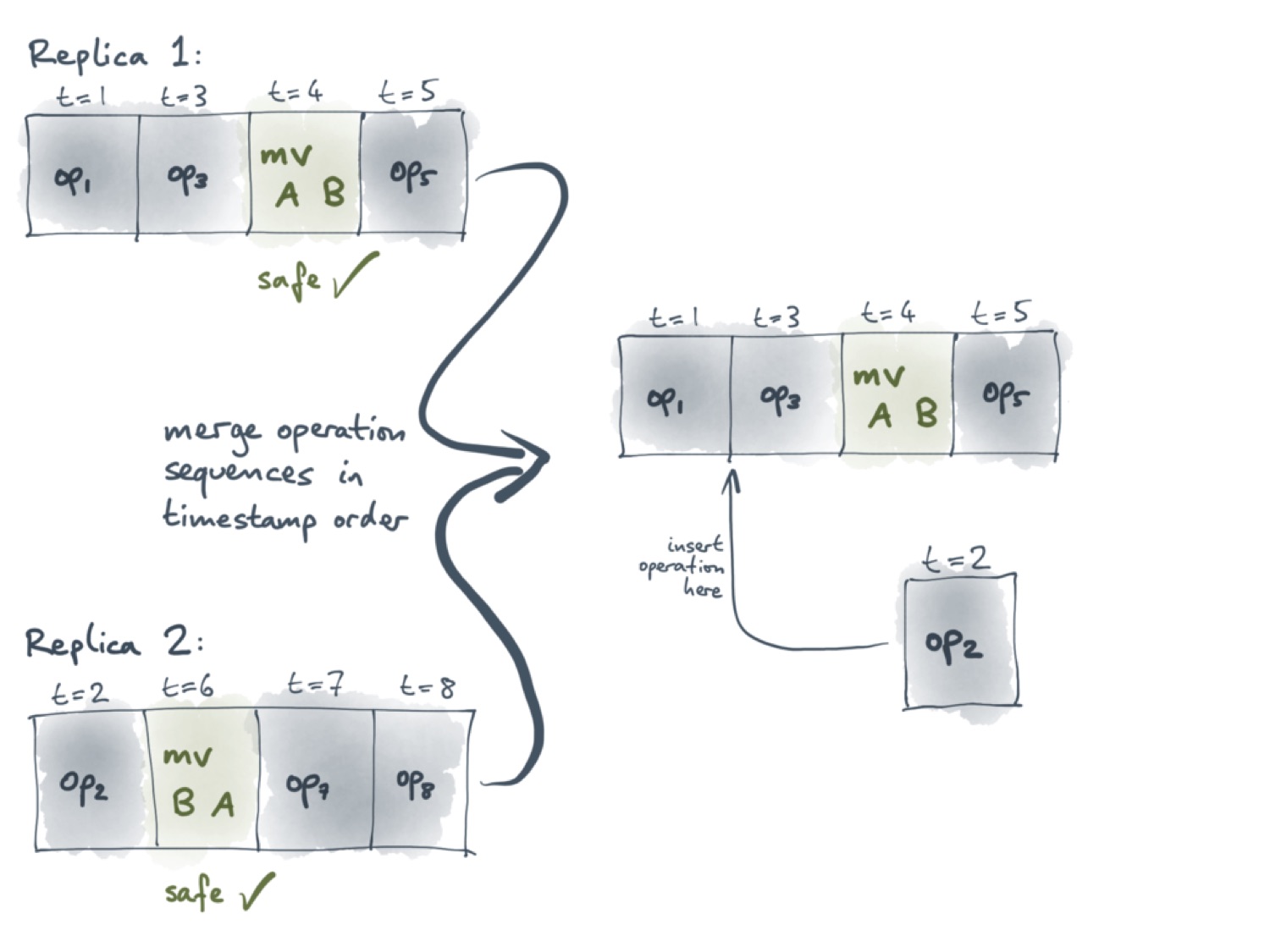
Мы не можем просто добавить op2 в конец списка, потому что тогда они не будут упорядочены по метке времени. Чтобы определить, какие операции безопасные, а какие — нет, важно знать порядок, в котором операции выполняются.
Мы изобрели простой, но весьма элегантный алгоритм для того, чтобы выполнять эту синхронизацию операций. Он представлен на следующем слайде.
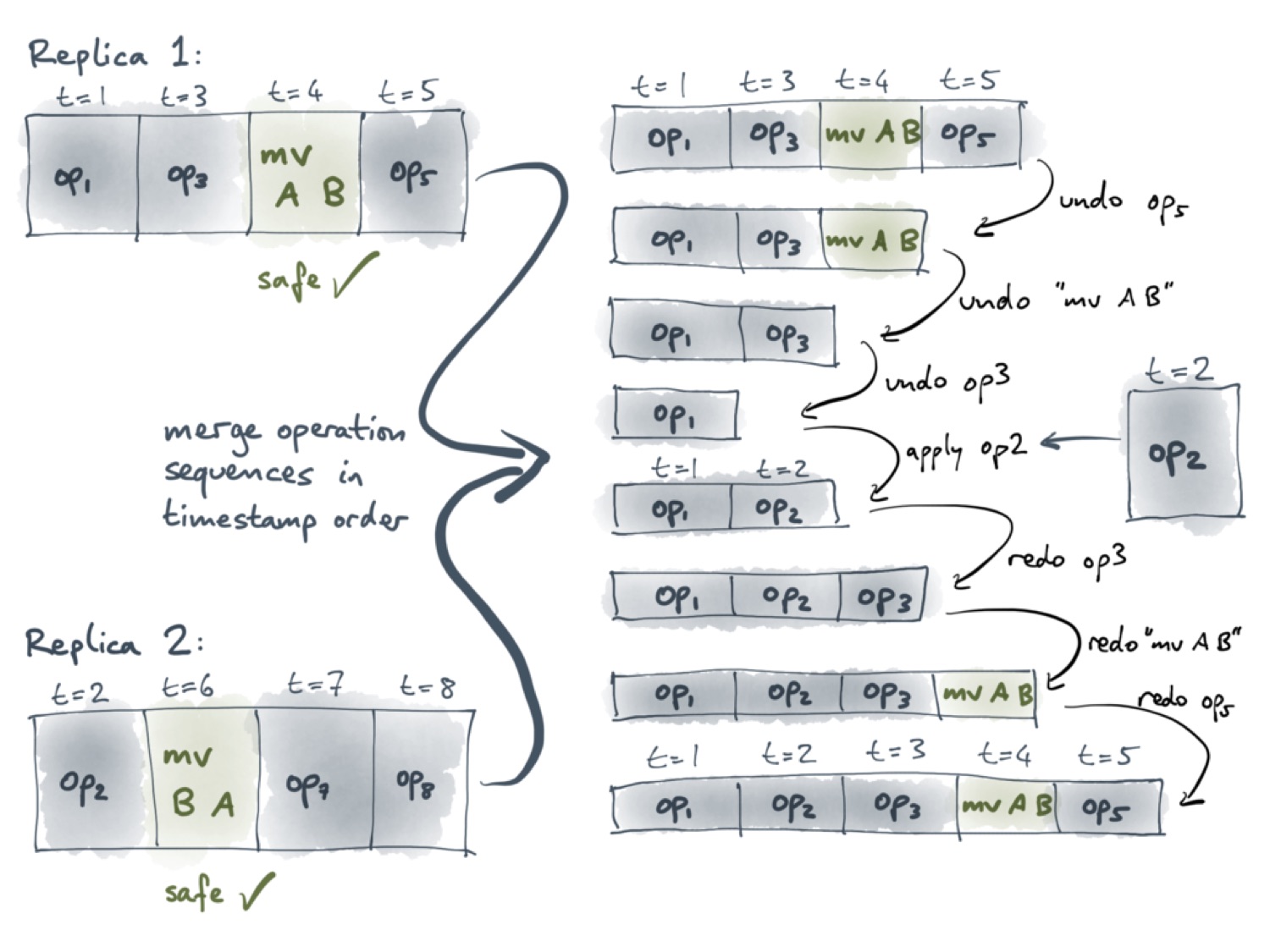
Для реализации этого алгоритма необходима возможность отмены операций. Как видим, первому пользователю нужно добавить новую операцию с меткой времени 2, в то время как у него уже есть операция с меткой времени 5. Поэтому ему необходимо отменить все операции с меткой времени больше 2, то есть операции op5, mv A B и op3. Теперь можно добавить операцию op2, а затем повторно применить все отменённые операции. При условии, что все операции полностью отменяемые, этот алгоритм генерирует список операций, применённых в порядке возрастания метки времени.
Все эти преобразования могут показаться ресурсозатратными. Какие-то издержки здесь, конечно, неизбежны. Чтобы определить их размер, мы поставили эксперимент с тремя репликами, которые мы развернули на трёх разных континентах, чтобы коммуникация происходила с большой задержкой. Затем мы запустили генерацию операций перемещения на этих репликах. Чем быстрее эти операции генерируются, тем больше отмен и повторов необходимо выполнять. Мы обнаружили, что время выполнения отдельной операции растёт линейно в зависимости от скорости применения операций, поскольку количество отмен и повторов растёт линейно в зависимости от числа операций. Тем не менее, в нашей довольно простой программе обрабатывалось около 600 операций в секунду. Это существенно меньше показателей, скажем, системы работы с большими данными, но значительно больше того, что необходимо приложению, запущенному одним пользователем в своей локальной системе для отдельного дерева. Так что для большого диапазона приложений такая производительность вполне допустима.
Теперь я хотел бы в общих чертах описать структуры данных, используемые в этом алгоритме (см. слайд).
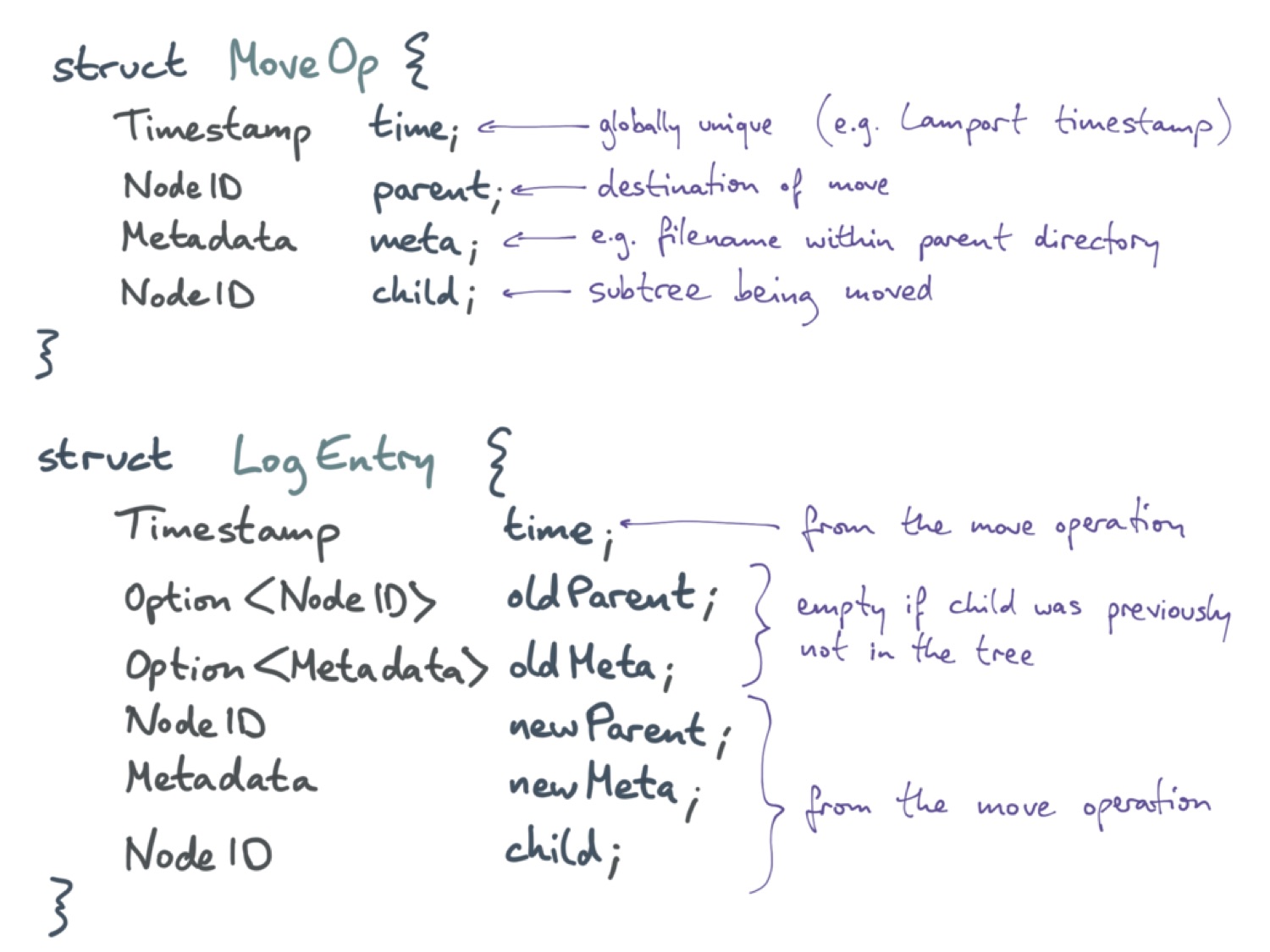
В сокращённом виде операция перемещения описывается структурой MoveOp. В каждой операции есть метка времени Timestamp. Такая метка должна быть уникальной для всего приложения; этого легко добиться с помощью, например, меток времени Лэмпорта. Далее, для операции необходим идентификатор, по которому можно обращаться к узлам дерева. Здесь child — это идентификатор перемещаемого узла, а parent — идентификатор узла назначения. Metadata meta — это метаданные отношения родительского и дочернего узла. Например, если мы работаем с файловой системой, в качестве meta может выступать имя файла. Обратите внимание, что здесь нигде не записано старое местоположение дочернего узла. Операция просто переносит узел со старого местоположения на новое.
Для того чтобы иметь возможность отменить и повторить операцию, необходим журнал и структура данных LogEntry. В ней можно записывать старое местоположение и старые метаданные дочернего узла при его перемещении. Тогда для отмены перемещения нужно просто поместить дочерний узел назад к старому родительскому.
Теперь мы можем описать алгоритм перемещения. Вначале нужно определить, что значит, что a является родительским узлом b. Формально это сделано на слайде.
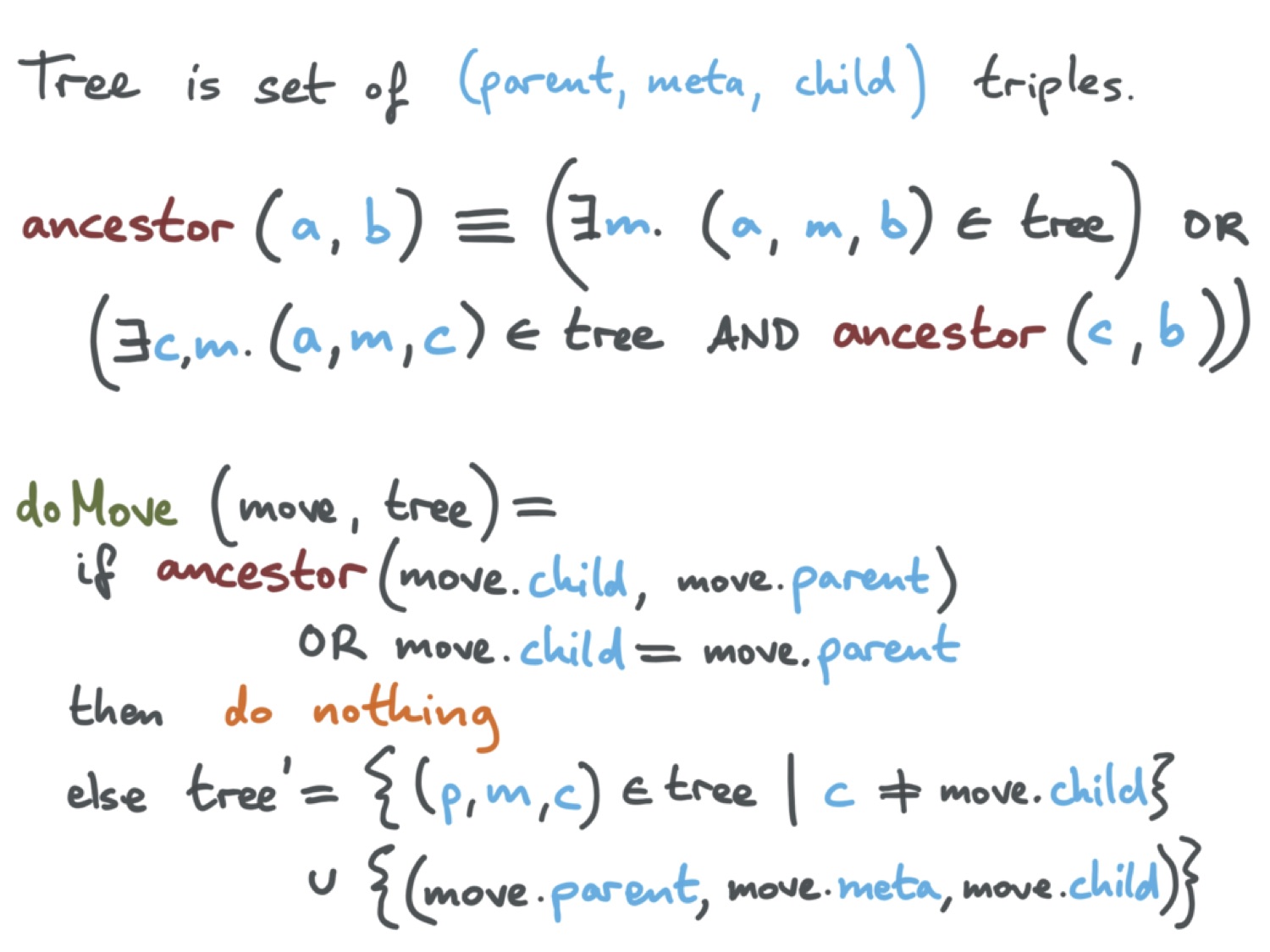
a является родителем b в том случае, если (a, m, b) ∈ дереву, то есть если a является прямым родителем b в дереве, или если есть узел c, такой, что a является родителем c, а c является родителем b. При таком определении операцию перемещения можно определить следующим образом. Вначале нужно проверить, не является ли перемещаемый узел родителем по отношению к своему родительскому узлу. Если да, то операция не выполняется, потому что она привела бы к возникновению цикла. То же самое в ситуации, когда дочерний узел идентичен родительскому. Если эти проверки успешно пройдены, то ситуация безопасна. Старое отношение можно удалить, а затем вставить новое отношение из дерева с новыми метаданными.
Мы доказали правильность этого алгоритма. А именно, мы показали, что для каждого дерева, с которым выполняется операция, сохраняется свойство дерева. Структура данных является деревом в случае, если у каждого узла есть уникальный родитель и если в дереве нет циклов. Выше мы показали, что операция перемещения не нарушает этих свойств. Кроме того, мы доказали, что эта операция является CRDT. То есть не важно, в каком порядке применяются операции — если два пользователя применяют один и тот же набор операций, то итоговое состояние одинаковое. Иначе говоря, мы доказали, что операции коммутативны.
CRDT с самого их появления преследовали проблемы с издержками метаданных. Для свойств CRDT всегда требовалось много места и сетевых ресурсов. Как вы помните, при редактировании текста мы присваивали уникальный идентификатор каждому символу в текстовом документе.
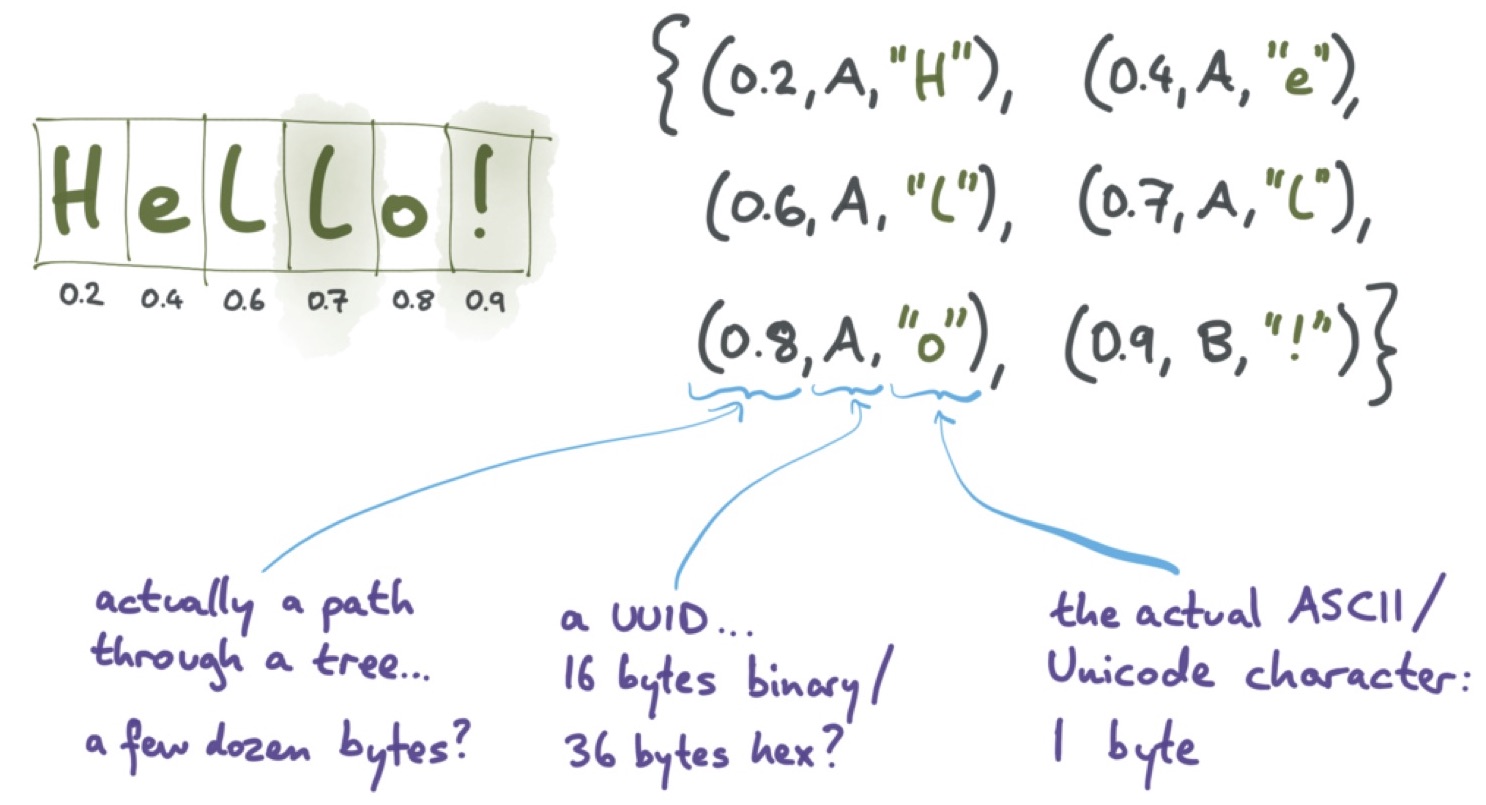
На следующем слайде показан текст, в котором использован такой алгоритм. Если работа идёт с английским текстом, то в кодировке UTF-8 один символ занимает один байт; для текста на русском языке каждый символ, скорее всего, будет занимать два байта. Это не так много; но в дополнение к этому необходим идентификатор позиции. Чаще всего в качестве него используется какой-нибудь путь в дереве, размер которого зависит от длины пути. Он с лёгкостью может занимать несколько десятков байт, если не сотню. Помимо него необходим идентификатор узла, то есть пользователя, который добавил данный символ. В итоге для символа, занимающего один байт, необходимо 100 байт метаданных, или даже больше. Согласитесь, ситуация крайне печальная.
Хочу поговорить об экспериментах, которые мы проводили в проекте Automerge, специальной реализации CRDT. За последние несколько месяцев я посвятил довольно много усилий тому, чтобы сократить издержки CRDT. Результаты вкратце представлены на следующем слайде.

Давайте обсудим их по порядку. Набор данных, на который мы тут смотрим — история редактирования одной статьи в академическом издании. Мы написали исследовательскую статью (в формате plain text-файла в формате LaTeX размером около 100 килобайт) с помощью текстового редактора собственной разработки, записав каждое нажатие клавиши во время этой работы. В общей сложности зафиксировано около 300 000 изменений: это включает все добавления и удаления символов, а также перемещения курсора. Мы хотели сохранить всю эту историю изменений, чтобы иметь возможность наблюдать за эволюцией документа (так же, как в системе контроля версий сохраняют прошлые версии проекта).
Проще всего этого добиться, если хранить журнал операций CRDT. Если записать такой журнал в формате JSON, он займёт около 150 мегабайт. С помощью gzip его можно сжать до примерно 6 мегабайт, но по сравнению со 100 килобайтами исходного текста без метаданных это всё равно огромный размер. Нам удалось, более эффективно закодировать данные и сократить размер файла метаданных до 700 килобайт (то есть где-то в 200 раз), при этом сохранив полную историю изменений. Если же отказаться от хранения перемещений курсора, размер можно сократить ещё на 22%. Далее, если убрать историю редактирования CRDT и оставить только метаданнные, необходимые для слияния текущей версии документа, размер сокращается до 228 килобайт. Это всего лишь в два раза больше размера исходного текста без метаданных. Если эти данные ещё и сжать в gzip, то мы получим чуть больше 100 килобайт. Далее, если избавиться от отметок полного удаления (tombstones), то мы получим 50 килобайт. Это то, что нужно для хранения уникальных идентификаторов для каждого символа. Но без отметок полного удаления мы уже не можем обеспечить слияния параллельно добавленных изменений.
Даже сохраняя целиком историю редактирования и отметки полного удаления, мы всё равно можем добиться весьма компактного размера итогового файла. Сейчас я постараюсь кратко объяснить, как это сделать. Мы храним информацию о всех выполненных операциях, и каждой операции присваивается уникальный идентификатор. В нашем случае таким идентификатором является метка времени Лэмпорта, это пара из счётчика и идентификатора узла. Как и в RGA, в нашем алгоритме для определения местоположения символа используется ссылка на идентификатор предшествующего символа. Далее все операции сохраняются в порядке, в котором они появляются в тексте. В итоге получается таблица вроде той, которая показана на следующем слайде.

В первых двух столбцах слайда хранятся метки времени Лэмпорта для каждой операции. Каждая строка здесь — операция вставки. Как видим, в третьем и четвёртом столбце указаны идентификаторы предшествующих символов. Здесь второй символ добавляется после первого, третий — после второго и так далее. В следующих двух столбцах указаны вставляемые символы в кодировке UTF-8, и количество байт, которое занимает каждый символ. Наконец, в последних двух столбцах записано, был ли символ удалён.
Эти данные можно сжать с помощью нескольких довольно простых приёмов. Каждый столбец этой таблицы можно закодировать отдельно. Первый столбец содержит числа 1, 2, 3, 4, 5, 6. К ним можно применить дельта-кодирование, то есть вычислить для каждого числа разницу между ним и предшествующим числом. Тогда мы получим 1, 1, 1, 1, 1, 1. К этому ряду можно применить кодирование длин серий, то есть сказать, что мы храним 6 повторений числа 1. Если к этому применить кодировку переменной длины для целых чисел, результат займёт всего два байта. Эта кодировка записывает самые короткие числа одним байтом, которые подлиннее — двумя, трёмя и тому подобное. Итак, для записи первого столбца нам потребовалось всего два байта, то есть ⅓ байта на операцию. Для второго столбца нужно создать таблицу подстановки, в которой идентификаторам пользователей присваиваются короткие числа. Тогда второй столбец можно представить как 0, 0, 0, 0, 0, 0. Дальше опять-таки можно применить кодирование длин серий, а затем кодировку переменной длины для целых чисел, и, как и в первом случае, результат будет занимать два байта.
Взглянем на столбец с символами UTF-8. Обратите внимание, что у нас есть отдельный столбец, в котором указана длина символа в байтах. Сам этот столбец легко закодировать только что описанным способом. А символы UTF-8 можно просто объединить в строку UTF-8 размером в 6 байт. Наконец, в последних двух столбцах мы записываем только тот факт, что мы удалили один символ. В дополнение ко всему этому нам необходимо совсем немного метаданных с информацией о том, когда произошло каждое изменение, какой диапазон идентификаторов операций, какие значения счетчиков для каждого изменения. В результате можно реконструировать состояние документа в любой момент времени в прошлом. Итак, мы сохранили целиком историю документа, но сжали её так, что она занимает совсем немного места.
На этом я хотел бы перейти к заключению. Как я уже сказал вначале, в работе с CRDT много трудностей. Сделать хорошую реализацию непросто, а плохую — легче лёгкого. Мы рассмотрели четыре проблемы, которые давно преследуют CRDT: чередование, операции перемещения в списках и деревьях, а также проблему издержек. Если вы хотите ознакомиться с дополнительной литературой по теме, вот список статей, в которых описан целый ряд CRDT для редактирования текста.
Logoot: Stéphane Weiss, Pascal Urso, and Pascal Molli: “Logoot: A Scalable Optimistic Replication Algorithm for Collaborative Editing on P2P Networks,” ICDCS 2009.
LSEQ: Brice Nédelec, Pascal Molli, Achour Mostefaoui, and Emmanuel Desmontils: “LSEQ: an Adaptive Structure for Sequences in Distributed Collaborative Editing,” DocEng 2013.
RGA: Hyun-Gul Roh, Myeongjae Jeon, Jin-Soo Kim, and Joonwon Lee: “Replicated abstract data types: Building blocks for collaborative applications,” Journal of Parallel and Distributed Computing, 71(3):354–368, 2011.
Treedoc: Nuno Preguiça, Joan Manuel Marques, Marc Shapiro, and Mihai Letia: “A Commutative Replicated Data Type for Cooperative Editing,” ICDCS 2009.
WOOT: Gérald Oster, Pascal Urso, Pascal Molli, and Abdessamad Imine: “Data consistency for P2P collaborative editing,” CSCW 2006.
Astrong: Hagit Attiya, Sebastian Burckhardt, Alexey Gotsman, Adam Morrison, Hongseok Yang, and Marek Zawirski: “Specification and Complexity of Collaborative Text Editing,” PODC 2016.
Наконец, вот список наших работ по темам, которые мы сейчас обсуждали.
Interleaving anomaly: Martin Kleppmann, Victor B. F. Gomes, Dominic P. Mulligan, and Alastair R. Beresford: “Interleaving anomalies in collaborative text editors”. PaPoC 2019.
Proof of no interleaving in RGA: Martin Kleppmann, Victor B F Gomes, Dominic P Mulligan, and Alastair R Beresford: “OpSets: Sequential Specifications for Replicated Datatypes”, May 2018.
Moving list items: Martin Kleppmann: “Moving Elements in List CRDTs”. PaPoC 2020.
Move operation in CRDT trees: Martin Kleppmann, Dominic P. Mulligan, Victor B. F. Gomes, and Alastair R. Beresford: “A highly-available move operation for replicated trees and distributed filesystems”. Preprint
Reducing metadata overhead: Martin Kleppmann: “Experiment: columnar data encoding for Automerge”, 2019.
Local-first software: Martin Kleppmann, Adam Wiggins, Peter van Hardenberg, and Mark McGranaghan: “Local-first software: You own your data, in spite of the cloud”. Onward! 2019.
Все слайды доступны в электронном виде. Спасибо большое за внимание!
Если вы дочитали этот доклад с Hydra 2020 до конца, похоже, что вы интересуетесь распределёнными вычислениями. В таком случае вам будет интересно и на Hydra 2021, которая пройдёт с 15 по 18 июня. Там будут как доклады от академиков, так и выступления людей из индустрии, которые имеют дело с параллельными и распределёнными системами в продакшне — на сайте уже анонсирован ряд докладов.
Комментариев нет:
Отправить комментарий