На протяжении пяти лет мы в Smart Engines рассказываем вам о том, как оптимизируем свой софт под процессорную архитектуру Эльбрус. Обычно мы делимся с вами феерическими результатами, когда на Эльбрусах нам удается распознавать почти так же быстро, как на топовых иностранных процессорах. Сегодняшняя статья посвящена описанию оптимизированных «внутренностей» одного крайне важного для всех систем компьютерного зрения алгоритма – быстрого преобразования Хафа. Кроме того, расскажем еще об одном крайне интересном семействе отечественных архитектур – микропроцессорах КОМДИВ.
Что такое преобразование Хафа и когда его применяют?
Преобразование Хафа было предложено в 1959 году Полом Хафом в качестве инструмента анализа фотографий следов частиц в пузырьковой камере [1]. По определению, преобразование Хафа ставит в соответствие каждому паттерну из определенного семейства (прямые, окружности, эллипсы) значение, равное сумме значений пикселей изображения, принадлежащих этому паттерну. Иногда вместо суммы вычисляют результат других заданных на множестве операций (подсчет минимального или максимального значения, вычисление среднее значения или произведения значений пикселей и т. д.). Например, преобразование Хафа для прямых (точнее – дискретных паттернов, аппроксимирующих прямые на изображении) вычисляет суммы по всем дискретным прямым заданной параметризации и структуры. Кстати, во многих источниках такое преобразование также носит название дискретного преобразования Радона [2, 3].
Результат преобразования Хафа (Хаф-образ) представляет собой изображение, в пикселях которого записаны результаты выбранной математической операций вдоль соответствующих паттернов. Его размер зависит от конкретного набора исследуемых паттернов и их параметризации.
Область применения преобразования Хафа в компьютерном зрении крайне обширна. Исторически преобразование Хафа разрабатывалось для решения задачи идентификации прямолинейных треков в пузырьковой камере. Поэтому наиболее известным применением преобразования Хафа является нахождение прямых или их отрезков на изображении [4]. Закономерное развитие – детектирования других паттернов [2]. Помимо выявления графических примитивов БПХ используется для решения самых разных задачах анализа изображений. В качестве примеров областей использования БПХ, весьма далеких от поиска отрезков, приведем бинаризацию [5] и сегментацию [6] изображений, а также задачу автоматического определения параметров оптических аберраций [7].
Существенным недостатком преобразования Хафа является высокая асимптотическая сложность: операций, где
– линейный размер изображения. Откуда взялась такая сложность? Давайте рассмотрим в качестве входа «серое» квадратное изображение с линейным размером
. Число всевозможных дискретных прямых на данном изображении –
, а длина таких прямых пропорциональна
. Следовательно, сложность вычисления сумм значений пикселей вдоль всевозможных прямых по данному изображению – заявленные
.
Поэтому на практике существует несколько схем, обеспечивающие более быстрое построения Хаф-образа (или его аппроксимации). Одна из таких схем была предложена в 1998 году М.Л. Брейди [8]. Именно она получила широко распространенное название «Быстрое преобразование Хафа» или, сокращенно, БПХ. Оценка сложности БПХ составляет .
Быстрое преобразование Хафа и пути его оптимизации
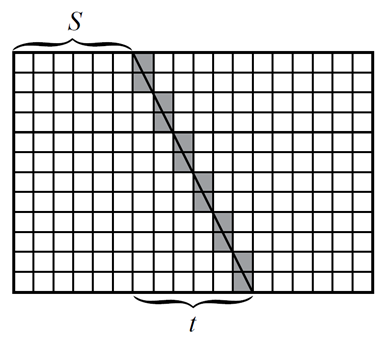
Алгоритм Брейди основан на принципе "разделяй и властвуй". Задача состоит в нахождении сумм значений пикселей вдоль отрезков, соединяющих «левый» и «правый» края изображения. Изображение делится пополам, в каждой части задача решается независимо. Для получения итоговой суммы на каждом из отрезков складываются ответы на «левой» и «правой» его половинах. В алгоритме БПХ пиксели прямых произвольного вида дискретно приближаются диадическими паттернами. Пиксели диадического приближения прямой на изображении размера удалены от исходной прямой не более, чем на
пикселей.
Диадический паттерн параметризуется точками пересечения с противоположными краями изображения и
, где
– целочисленный сдвиг паттерна,
– целочисленный наклон,
– сторона изображения. Такому паттерну соответствует точка
в Хаф-образе, значение в которой равняется сумме значений пикселей вдоль соответствующего паттерна.
Рассмотрим реализацию алгоритма. Пусть дано изображение размером причем
. На следующем листинге приведена рекурсивная реализация алгоритма Брейди на языке MATLAB, опубликованная в работе [9].
function h = fht2(I)
n = size(I, 2);
if n < 2
h = m;
return
end
h = mergeHT(fht2(I(:, 1 : n / 2, :)), fht2(I(:, (n / 2 + 1) : n, :)));
end
function h = mergeHT(h0, h1)
[m, n0, o] = size(h0);
n = 2 * n0;
h = zeros(m, n, o);
r = (n0 - 1) / (n - 1);
for i = 1 : n
t = i - 1;
t0 = round(t * r);
s = t - t1;
h(:, i, :) = h0(:, t0 + 1, :) + [h1(s + 1 : m, t0 + 1, :); h1(1 : s, t0 + 1, :)];
end
endКак видно, в данной реализации алгоритм Брейди состоит из двух частей. Первая часть представляет собой рекурсивное разбиение изображения на левую и правую части до тех пор, пока мы не разобьём изображение на векторов, где
– ширина изображения. Вторая часть задает объединение пар таких частей в одно целое, до тех пор, пока не получится искомый Хаф-образ. Таким образом, алгоритм Брейди, за счет принципа «разделяй и властвуй», фактически, сводится к многократному выполнению векторной операции суммирования, позволяя при этом получить искомую аппроксимацию образа за меньшее число операций.
Пути оптимизации БПХ
Реализация алгоритма Брейди для промышленных распознающих систем, выполненная на языке общего назначения, позволяет устранить «узкие» с вычислительной точки зрения места, представленного выше алгоритма на MATLAB:
-
исключить избыточное копирование данных;
-
развернуть рекурсию в цикл для большего контроля за использованием памяти и минимизации накладных расходов.
Избавление от первого «узкого» места происходит путем перехода от манипуляции столбцами значений к манипуляции с указателями. При этом само изображение следует представить в виде массива указателей. Тогда для того, чтобы поменять местами два столбца, достаточно поменять местами указатели в массиве.
Второе «узкое» место – рекурсия. Несложно видеть, что рекурсивная процедура fht2core фактически строит полное двоичное дерево из интервалов по горизонтальному индексу изображения. Далее, с каждым вызовом процедуры mergeHT, проводится объединение двух интервалов и удаляются два листа с общим родителем, превращая последнего в лист. Так происходит поэтапное объединение всех интервалов, пока не останется один конечный интервал и мы не получим искомую аппроксимацию Хаф-образа. Несмотря на то, что алгоритмически мы строим дерево, программно реализовать необходимо последовательное заполнение массива интервалов размером
. После чего – двигаться по массиву в обратном направлении, объединяя интервалы в соответствии с процедурой
mergeHT.
Наш опыт FHT на Эльбрус
Как вы знаете, мы все свои технологии переносим на Эльбрус. И не просто портируем по известному принципу «главное запустилась и отлично», а со всей ответственностью подходим к этой задаче. Все наши продукты полноценно работают на разных вычислительных платформах.
Преобразование Хафа, точнее БПХ, является одним из ключевых элементов в наших продуктах. К сожалению, на сегодняшний день БПХ пока еще не представлено в библиотеке EML, поэтому эффективная реализация алгоритма легла на наши плечи.
Дополнительно к приемам, описанным выше, мы векторизовали некоторые операции за счет применения специфических векторных инструкций.
В результате, как мы уже писали здесь на Хабре, на наших отечественных Эльбрусах нам удалось:
Теперь КОМДИВ. А что такое КОМДИВ?
Отечественные вычислительные платформы не заканчиваются на Эльбрусах (про особенности и тонкости которых мы так любим рассказывать на Хабре) и Байкалами (наш опыт программирования для этих платформ нами также был уже представлен на Хабре). Еще достаточно широко распространены в узких кругах компьютеры КОМДИВ-64. А что это за электронный зверь?
КОМДИВ-64 – это семейство 64-разрядных микропроцессоров, разработанных в научно-исследовательском институте системных исследований (НИИСИ) Российской Академии наук. Микропроцессоры реализуют набор команд архитектуры MIPS IV (ISA).
Микропроцессор цифровой обработки сигналов 1890ВМ9Я изготавливается по технологии 65 нм, обеспечивает частоту функционирования до 1 ГГц и производительность до 80 Гфлопс.
В составе SoC 1890ВМ9Я присутствует сопроцессор комплексной арифметики CPCA. CPCA имеет отдельную накристальную память команд (64 Кбайт), единый вычислительный конвейер, способный выбирать на исполнение одну вычислительную и одну команду пересылки и управления за такт и четыре вычислительных секции – 4 SIMD. Каждая вычислительная секция содержит 64 Кбайт накристальной памяти данных и набор из 64 64-разрядных регистров общего назначения. В составе сопроцессора имеется также набор разделяемых секциями 16 адресных регистров и 16 регистров общего назначения. К управляющим командам относятся также и команды чтения/записи накристальных памятей данных, скорость доступа к накристальным памятям – 16 байт/такт в каждой секции. CPCA выполнен как сопроцессор управляющего универсального процессора архитектуры MIPS64 Release 1. Загрузка и выгрузка данных из памятей секций осуществляется при помощи контроллера прямого доступа к памяти (ПДП), также заимствованного из СнК 1890ВМ7Я. Контроллер позволяет обмениваться данными с основной памятью со скоростью 16 байт/такт. Выполнение операций загрузки и выгрузки данных может быть совмещено с вычислениями.
КОМДИВ и БПХ
Система команд CPCA содержит инструкции для работы с комплексными числами – парами 32-разрядных вещественных чисел формата ISO 60559. Каждая секция имеет 10 конвейеризированных сумматоров и умножителей, полностью задействованных в инструкции «бабочка Фурье», которая использует помимо регистров еще и накристальную память коэффициентов. Инструкции «умножение вещественной 2x2-матрицы на вещественный 2d-вектор» и «комплексное умножение с накоплением», использующие только регистры, задействуют до 8 сумматоров и умножителей. Таким образом, пиковая производительность CPCA при штатной тактовой частоте 800 МГц составляет 32 Гопс (10 оп./такт в 4 секциях при 800 МГц) или 25.6 Гопс при использовании регистровых инструкций.
Как было отмечено выше, ключевой операцией в алгоритме БПХ является поэлементное суммирование двух столбцов, где один операнд циклически сдвинут. На операции сложения двух векторов производительность CPCA не превышает 4.2 Гопс. Действительно, в то время как сумматоры способны выполнять по 2 сложения каждый такт в 4 секциях (команда сложения двух пар чисел – инструкция psadd), т.е. производительность сумматоров составляет 6.4 Гопс при 800 МГц, однако для достижения такого показателя производительности данная операция требует загрузки 4 чисел из локальной памяти и выгрузки 2 чисел в локальную память каждый такт в каждой секции, т.е. должна достигаться скорость обмена с локальной памятью не менее 19.2 Гчисел/сек при 800 МГц. Пропускная способность шины между сумматорами и накристальной памятью секции ограничена скоростью 4 числа/такт или 12.8 Гчисел/сек при 800 МГц. Таким образом, эффективная производительность сумматоров оказывается в 1.5 раза меньше пиковой.
Более того, контроллер ОЗУ типа DDR3 в составе СнК 1890ВМ9Я работает на частоте 400 МГц, что определяет пиковую скорость обмена между CPCA и ОЗУ в 6.4 Гбайт/сек (16 байт/такт при 400 МГц) или 1.6 Гчисел/сек. При таком ограничении производительность СнК в целом на операции сложения двух векторов не превысит 533 Мопс (3 числa/оп. при скорости 1.6 Гчисел/сек). Следует понимать, что это пиковая теоретическая производительность рассматриваемой операции, на практике такая производительность недостижима.
Таким образом, загрузка CPCA при выполнении быстрого преобразования Хафа составит около 12% от эффективной производительности операции сложения и менее 2% от общей пиковой производительности сопроцессора. Приведенные оценки позволяют определить ключевые направления разработки алгоритма БПХ для CPCA. А именно, что достижение оптимальной реализации вычислительной процедуры практически бессмысленно, поскольку основной вклад в производительность вносят лишь обмены CPCA с внешней памятью. В частности, это означает:
-
необязательно задействовать все 4 секции, производительность одной секции (1 Гопс) в 2 раза превышает пиковую производительность обменов с ОЗУ;
-
совмещение обменов с вычислениями не приводит к заметному повышению производительности (доля вычислений составляет около 12% от общего объема работы);
-
для повышения производительности БПХ необходимо сократить число обменов между ОЗУ и CPCA, иными словами – в алгоритме БПХ требуется выявить повторную используемость данных.
В процедуре mergeHT на два входных среза h0 и h1 с общим числом столбцов n приходится n сумм, то есть большинство столбцов участвует в двух суммах, причём с разными циклическими сдвигами. В случае, когда результирующий срез четного размера и n0 = n1 = n / 2, каждая пара столбцов преобразуется в два новых столбца суммированием с разным циклическим сдвигом. В случае, когда результирующий срез нечётного размера, выделить такие пары не удается, но каждый столбец (кроме одного начального), участвует как минимум в двух суммах подряд (в порядке увеличения индекса).
Повторное использование столбцов позволяет сократить загрузку/выгрузку данных в локальную память сопроцессора CPCA в 1.5 раза: каждый столбец в рамках фиксированной операции объединения двух срезов мы загружаем ровно один раз. Пиковая теоретическая производительность при такой оптимизации возрастет до 800 Мопс, а оценка загрузки CPCA повысится до 18%.
По существу, с точки зрения оценки производительности задача БПХ свелась к задаче копирования массивов в памяти. А производительность этой операции можно измерить штатными тестами из состава библиотеки цифровой обработки сигналов для CPCA. Тест производительности функции копирования комплексных векторов показывает, что достигаемая на практике производительность копирования составляет 1.88 Гбайт/сек при размере копируемых данных 32 КБайта. Переводя полученные результаты в единицы, используемые здесь, получаем, что практически достижимая верхняя оценка производительности БПХ составляет 470 Мопс.
Измеренная производительность БПХ на изображении 5439 × 5439 составила 1.1 изображение/сек или 406 Мопс, то есть 86% от полученной ранее верхней оценки производительности. Производительность ожидаемо возрастает с увеличением размера изображения. В частности, производительность обработки изображений 512 × 512 составляет 116 Мопс (49 изобр./сек), 1024 × 1024 –191 Мопс (18 изобр./сек), 2048 × 2048 – 286 Мопс (6 изобр./сек), 4096 × 4096 – 378 Мопс (1.8 изобр./сек).
Заключение
В сегодняшней статье мы постарались раскрыть сразу несколько моментов. Во-первых, еще один раз рассказали про такой замечательный в компьютерном зрении инструмент, как преобразование Хафа (быстрое преобразование Хафа). Во-вторых, очередной раз помянули вспомнили отечественные процессоры, которые, кстати говоря, совсем неплохи для решения отдельных задач. И наконец, детально рассказали на какие ухищрения приходится идти в процессе оптимизации софта.
Хотелось бы выразить огромную благодарность коллективу ФГУ ФНЦ НИИСИ РАН за предоставленные тестовые образцы оборудования и совершенно бесценные консультации по написанию «правильного» софта для КОМДИВ.
Спасибо.
Данная публикация подготовлена по материалам научной статьи «Эффективная реализация быстрого преобразования Хафа с использованием сопроцессора CPCA», авторы Ф. А. Аникеев, Г. О. Райко, Е. Е. Лимонова, М. А. Алиев, Д. П. Николаев, принятой в печать в журнал «Программирование».
Список литературы
-
Hough P. Machine analysis of bubble chamber pictures // Proc. of the International Conference on High Energy Accelerators and Instrumentation, Sept. 1959. – 1959. – P. 554-556.
-
Mukhopadhyay P., Chaudhuri B. B. A survey of Hough Transform // Pattern Recognition. – 2015. – Vol. 48. – No. 3. – P. 993-1010.
-
Hassanein A. S. et al. A survey on Hough transform, theory, techniques and applications // arXiv preprint arXiv:1502.02160. – 2015.
-
Duda R. O., Hart P. E. Use of the Hough transformation to detect lines and curves in pictures // Communications of the ACM. – 1972. – Vol. 15. – No. 1. – P. 11-15.
-
Ершов Е. И., Асватов Е. Н., Николаев Д. П. Робастная ортогональная линейная регрессия для маломерных гистограмм // Сенсорные системы. – 2017. – Т. 31. – №. 4. – С. 331-342.
-
Nikolaev D. P., Nikolayev P. P. Linear color segmentation and its implementation // Computer Vision and Image Understanding. – 2004. – Vol. 94. – No. 1-3. – P. 115-139.
-
Kunina I. A., Gladilin S. A., Nikolaev D. P. Blind compensation of radial distortion in a single image using fast Hough transform // Computer Optics. – 2016. – Vol. 40. – No. 3. – P. 395-403.
-
Brady M. L. A fast discrete approximation algorithm for the Radon transform // SIAM Journal on Computing. – 1998. – Vol. 27. – No. 1. – P. 107-119.
-
Ершов Е. И., Терехин А. П., Николаев Д. П. Обобщение быстрого преобразования Хафа для трехмерных изображений // Информационные процессы. – 2017. – Т. 17. – №. 4. – С. 294-308.
Комментариев нет:
Отправить комментарий