(c) Илья Мамонтов, 2021
Согласно общепринятой теории фазовые соотношения в спектре звука не важны для восприятия тембра. Как выясняется, это справедливо лишь отчасти (для частот выше 200 Гц). Для звуков низкой частоты (менее сотни Гц) начинает работать другой механизм, в чем и предлагаю убедиться.
Вначале небольшая предыстория.
Мне как-то потребовался периодический звуковой сигнал с достаточно широким спектром (много гармоник). Таким свойством обладает последовательность очень коротких импульсов, вот только их энергия заключена в коротких интервалах времени. При сохранении средней мощности сигнала это приводит к росту пиковой амплитуды. А диапазон что в аналоге, что в цифре – он ограничен. Лучшими амплитудными свойствами обладает двуполярный импульс, но у меня возник вопрос – а можно ли создать такой широкополосный периодический сигнал, чтобы его энергия была равномерно «размазана» по всему периоду? И как он будет выглядеть, если его спектр ограничить некоторой максимальной частотой (для реализации в цифре?).
Интуиция подсказывала варьировать начальные фазы гармоник, но готового решения я нигде не нашел. Тогда начались эксперименты, во время которых выяснилось, что общепринятое представление об отсутствии влияния фазы на восприятие тембра справедливо лишь отчасти. Для высоких звуков это выполняется на 100%, но перестает работать для звуков низкой частоты. Сей факт указывает на то, что в низкочастотной области начинает действовать другой механизм, отличный от спектрального анализа, вроде бы как производимого органом слуха. Вопрос требует дальнейшего изучения (с возможным пересмотром физиологии), здесь же просто демонстрируется этот факт.
Итак, сгенерируем тестовый сигнал с ограниченным спектром – основной тон и первые 19 гармоник (со 2-й по 20-ую), все – с одинаковыми амплитудами. Выбор такого сигнала обусловлен возможностью свободно менять его частоту и не заморачиваться при этом с критерием Котельникова-Найквиста (невыполнение которого приводит к появлению побочных частот-призраков) при экспериментах на компьютере. При стандартной частоте дискретизации 44100 Гц это даст максимальную позволенную частоту основного тона 1100 Гц, что вполне достаточно для покрытия музыкального диапазона (более высокие ноты хоть и употребляются на практике, но воспринимаются больше как писк). Для тестирования выберем три частоты, отстоящие друг от друга достаточно далеко – 40, 200 и 800 Гц.
Если суммировать косинусоиды, то получим форму сигнала, приближающуюся к дельта-функции (короткий высокий импульс):

Если суммировать синусоиды (это те же косинусоиды, только сдвинутые на угол пи/2), получим последовательность двуполярных импульсов:
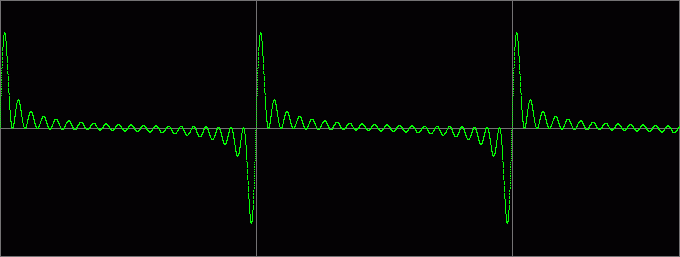
Пока все идет в соответствии с теорией, и даже звон, появляющийся из-за ограниченности спектра, хорошо слышен. Ниже приведен пример звучания «косинусоидального» и «синусоидального» сигналов, следующих друг за другом с небольшим интервалом. Если зациклить такой фрагмент, то можно настроиться на выявление малейших отличий.
Слушать: «Косинусоидальный» импульсный сигнал, затем «синусоидальный» (800 Гц)
Отличия (если нет перегруза, а звуковоспроизводящая аппаратура обладает высоким качеством) не обнаруживаются – несмотря на то, что формы сигналов кардинально различаются. Не будет разницы и если понизить частоту:
Слушать: «Косинусоидальный» импульсный сигнал, затем «синусоидальный» (200 Гц)
Слушать: «Косинусоидальный» импульсный сигнал, затем «синусоидальный» (40 Гц)
Так в чем вопрос? – спросите вы. А в том, что мы рассмотрели только два частных случая, а в жизни их существует бесчисленное множество. И некоторые могут выбиваться из правила.
Не будем изобретать что-то изощренное, а просто смоделируем распространение звука в дисперсной среде – такой, где скорость распространения зависит от частоты. Простейший случай – когда высокие частоты распространяются быстрее низких по пропорциональному закону. Сигнал при этом будет описываться такой функцией:
s(t) = cos(2 пи f•(t+0)) + cos(2•2 пи f•(t+k)) + cos(3•2 пи f•(t+2•k)) + cos(4•2 пи f•(t+3•k)) + ...
где k – достаточно малое число. Назовем его «коэффициент дисперсии», а физический смысл заключается в степени зависимости фазового сдвига гармоники от ее номера. Величине 0 соответствует отсутствие фазовых сдвигов, величине 0,25 (это уже чрезвычайно много) – набег на четверть периода для каждой последующей гармоники (имеется в виду период результирующего сигнала), величине 0,5 (это колоссально много) – набег на половину периода, а величине 1,0 (это уже неприлично много) – набег на целый период. Отрицательным значениям соответствует ситуация, когда высокие частоты распространяются медленнее низких.
Вот как выглядит постепенное увеличение k:
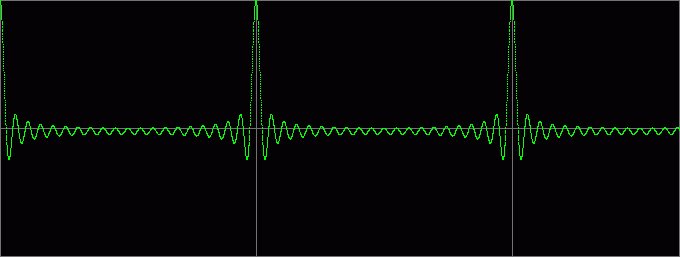
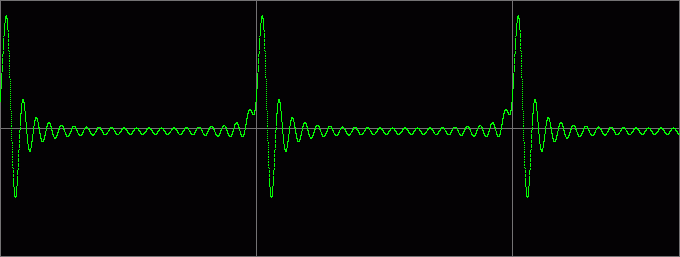
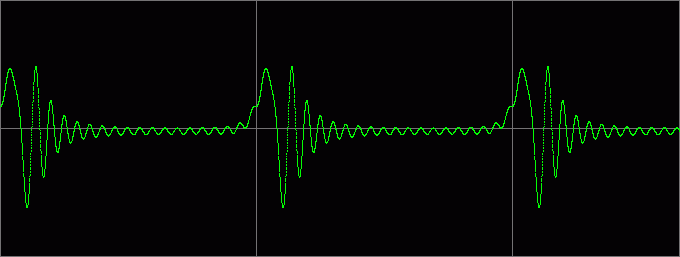
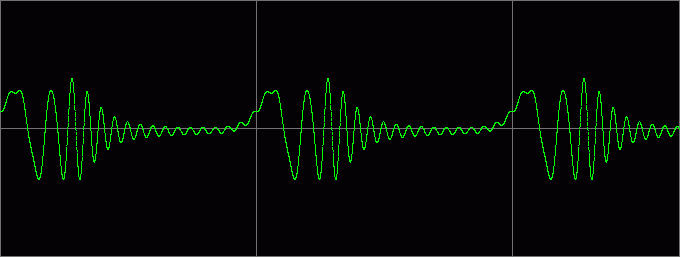
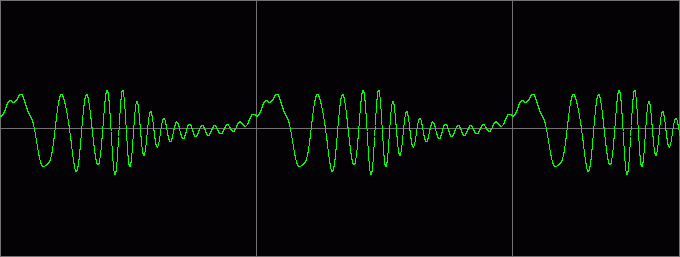
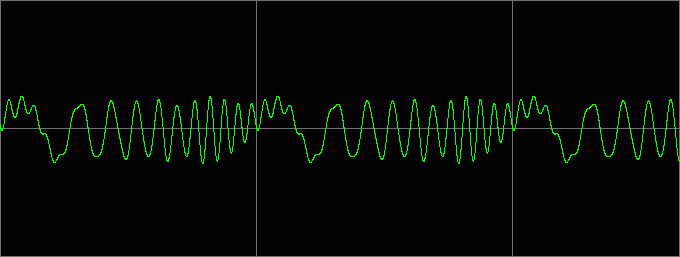
Примеры звучания (k=0,05):
– 40 Гц
– 200 Гц
– 800 Гц
Попутно замечаем, что амплитуды «волн» выравниваются, а следовательно, запас по амплитуде растет (немного не доходит до 4-х кратного).
А теперь послушайте, как звучит этот «размазанный» сигнал. Как и в предыдущем случае, для сравнения в фонограмму добавлен второй сигнал, в качестве которого взят исходный (с k =0). Итог – на 200 и 800 Гц отличий нет (на 200 Гц при использовании хороших головных телефонов, может, кто-то и отметит едва уловимую разницу), а вот на 40 Гц отличие становится заметным даже неискушенному слуху.
Здесь можно было бы остановиться (для опровержения достаточно одного контрпримера), либо рассмотреть другие экзотические случаи, но мне стало интересно – что же будет дальше?
А дальше импульс «расползается» настолько сильно, что затрагивает уже несколько последующих периодов. В результате сигнал становится похожим на случайный (внутри периода, конечно):

Примеры звучания (k=0,1):
– 40 Гц
– 200 Гц
– 800 Гц
Дальнейшее увеличение k ничего нового не дает – характер картинки остается тот же. Все те же волны, возникающие случайно на разных местах и с разными амплитудами. Между тем, меняя k, можно наткнуться на несколько «магических» значений, при которых хаос неожиданно сменяется некоторым порядком. Вот самые яркие случаи:
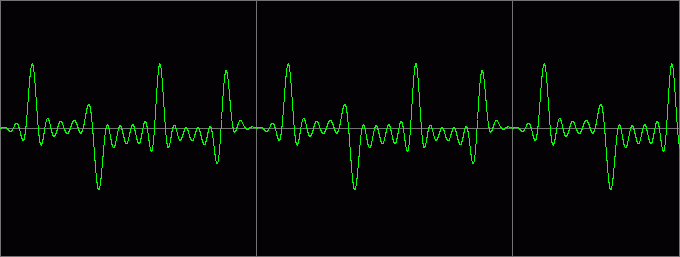
Пример звучания (k=0,25):
– 40 Гц

Пример звучания (k=0,5):
– 40 Гц
А при k=1 вообще получается исходный сигнал (а чего вы ждали – это напрямую следует из формулы)!
Выяснилось, что упорядочивание происходит при k, равном отношению целых чисел (2/3, 3/4 и т.д.). Вспоминая Архимеда, Леонардо да Винчи и прочих великих математиков древности, любивших играться с числами, можно предположить, что наименьшую упорядоченность даст «золотое сечение» (G=[корень(5)-1]/2 = 0,61803..), либо его производные (G/2, G/3, 1/G, 1/2G и т.д.). Соответствующий случай приведен ниже.

Примеры звучания (k=0,1):
– 40 Гц
– 20 Гц
Я перестал приводить примеры для 200 и 800 Гц, т.к. отличий в звучании все равно нет. Вместо этого в последнем случае добавился пример для 20 Гц – чтобы разница проявилась во всем своем блеске. Чтобы сравнить звучания сигналов с разными k между собой (а не с эталонным сигналом), используйте звуковые редакторы и команды «вырезать»–«вставить». Таким же способом можно размножить фрагмент – чтобы не использовать зацикливание.
На этом пока, собственно, все. На низких частотах прослеживается зависимость тембра звука от фазовых соотношений. Помимо спектрального анализа орган слуха начинает вовлекать другой механизм, суть которого, по-видимому, заключается в прямом восприятии пульсаций. Также показано, как можно создать звуковой сигнал с широким спектром, но не имеющий высоких «выбросов». Выигрыш по сравнению с импульсным сигналом достигает почти четырех раз (для данного случая), однако к этому следует подходить с осторожностью, т.к. на низких частотах меняется тембр.
P.S. Когда я это все написал, то наткнулся на статью «Тембр и фазовый спектр» (автор Алдошина И.А., журнал "Звукорежиссер", 2001, №4), где рассказывается об экспериментах с похожими сигналами. Там же отмечается появление второго тона при складывании чередующихся косинусоидальных и синусоидальных гармоник с нулевыми начальными фазами (вот вам и экзотика). Интересно, что именно такая форма получается при k=0,5 (см. выше). Послушайте еще раз это звучание. Лично у меня (и не только) подобные сигналы ассоциируются больше с тарахтением мотора, чем с музыкальными звуками (словарь прилагательных в статье можно было бы дополнить термином «motor boating»). При этом сомнений нет – уверенно ощущается «тарахтение» и на удвоенной частоте.
Комментариев нет:
Отправить комментарий