Добро пожаловать в наше уютное конспирологическое логово. Сегодня мы будем рассматривать тени на фотографиях с Марса, округлять числа и писать отвратительный код.

В этом выпуске: астрономические наблюдения теней в пустыне, аугментация ушей, заглядывание за левый край видео, гадание по фотографиям и особенности работы GSCMOS матриц семилетней давности.
Лифт (предположительно работает):
-
Вертолеты на Марсе
1.1 Оценка расстояния до Марса
1.2 Ошибки? -
Вертолеты жужжат
2.1 Blade Passage Frequency
2.2 Эффект Доплера
2.3 Оцениваем скорость вертолета
2.4 …расстояние до марсохода
2.5 …точки взлета и посадки
2.6 …дальность полета
2.7 …план полета
2.8 Симуляция эффекта Доплера и сравнение
2.9 Ошибки?
2.10 Всякое
2.11 Оффтоп 1: Пассивный Доплер-радар
2.12 Оффтоп 2: Марсианская аэродинамика -
Вертолеты не отбрасывают тень
3.1 Оценка характеристик камеры и оптики
3.2 Почему лопасти прозрачные?
3.3 …они прозрачные в ИК?
3.4 Оффтоп 3: ИК-фотография для бедных
3.5 …они путешествуют во времени?
3.6 Оценка эффективности затвора
3.7 Откуда на фото градиент яркости?
3.8 Передний край
3.9 Ground truth
3.10 Симуляция глобального затвора
1. Вертолеты на Марсе
Маленький вертолет летает на Марсе, но где летает Марс? Насколько он дальше от Солнца чем Земля? Насколько меньше света достается камерам и солнечной батарейке?
У меня нет фотографии солнечной батарейки, чтобы по ней гадать, зато есть фотография тени от солнечной батарейки:


Тень должна быть шириной с саму батарейку (165мм), ведь лучи от солнца параллельны. Можно взять ширину тени на фото и пересчитать пиксели в миллиметры.
2086 пикселей = 165мм. 0.079мм/пиксель.
Зачем нам это, и почему где-то в середине тени, а не по её верхней границе? Потому что перспектива заваливает размеры, а именно на этой линии слева нет особо крупных камней.
Как раз там, где тень переходит в свет.

Солнце, хоть и находится очень далеко, имеет заметный угловой размер на небе и границы теней от него не идеально резкие. Хуже того, ширина полутени (L) очень просто зависит от расстояния до предмета отбрасывающего тень (h), и углового размера Солнца (a)
Вооружившись этим знанием, а так-же тем, что высота Ingenuity составляет 49см, а солнечная батарея находится на самой его макушке, мы можем прикинуть, насколько далеко находится Марс.
Для начала измерим полутень. Песок и камни мешают это сделать вручную, но их можно усреднить. Повернем фотографию так, чтобы граница тени была строго вертикальна, берем кусок без камней, и сохраняем.

Дальше надо преобразовать картинку в Ч/Б, усреднить все строки и построить график яркости от координаты X. 10 строчек на питоне:
import sys
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
im = Image.open(sys.argv[1]).convert('L')
im.resize((im.size[0],1), Image.ANTIALIAS)
plt.plot(np.arange(im.size[0]), np.array(im).mean(axis=0))
plt.show()
Яркость начинает падать примерно на x=43 и перестает на x=80. Ширина полутени получается 37 пикселей, или ~3мм.
Теперь, проведем такой-же эксперимент на Земле. Тень от предмета на расстоянии 49см:
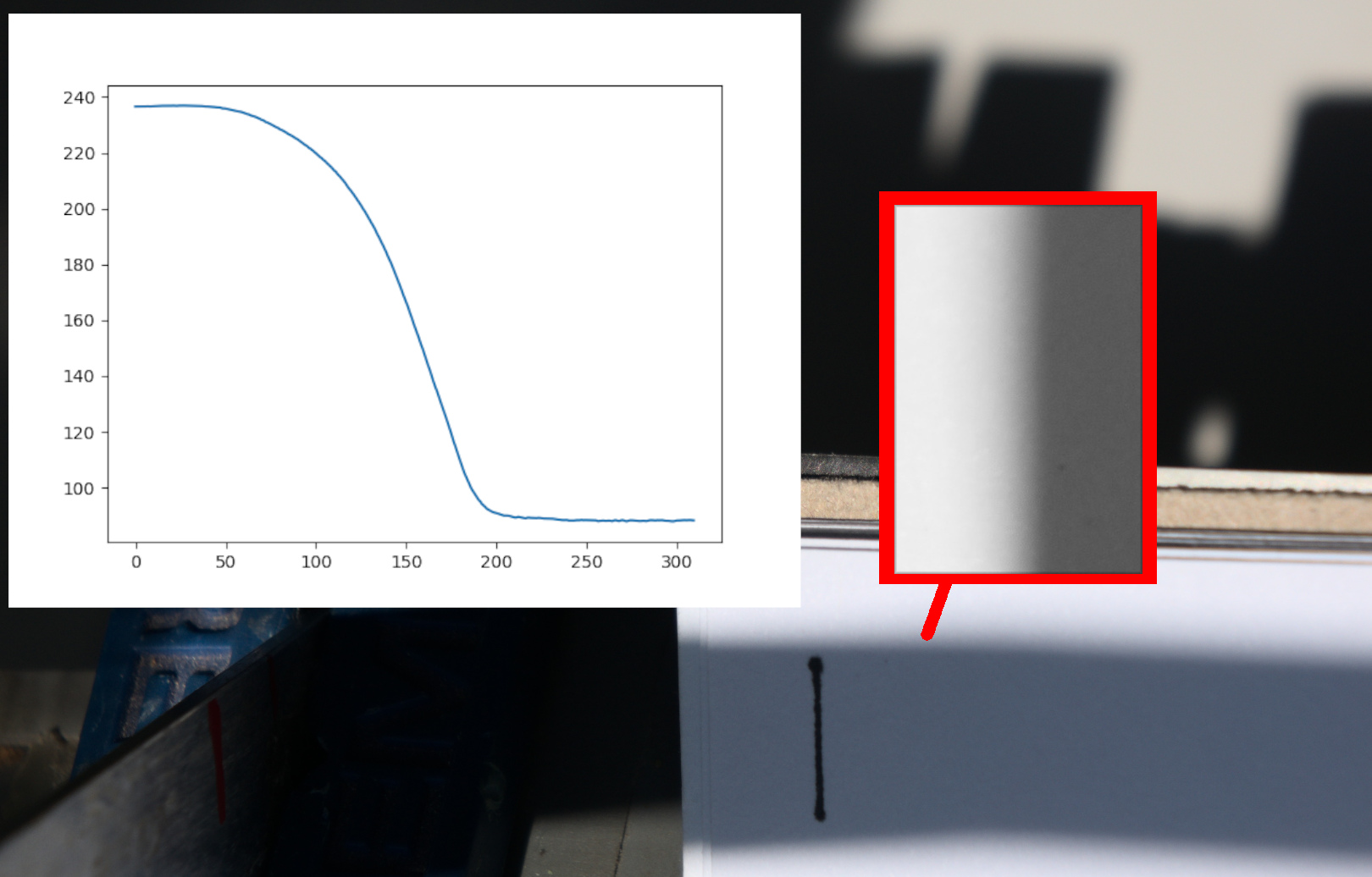
Ширина полутени получилась 4.56мм. Делим одно на другое и узнаем, насколько Марс дальше от Солнца, чем Земля: 4.56/3 = 1.52. А значит света на Марсе в 1.52^2 ≈ 2.3 раза меньше (без учета особенностей атмосфер обоих планет).
Теперь, расстояние от Солнца до Марса: отношение полутени к высоте солнечной батареи 3/490 = 0.00612. Диаметр солнца 1.3927 миллионов километров, значит расстояние 1.3927/0.00612 = 227.5 миллионов километров.
1.2 Ошибки?
На самом деле расстояние от Марса до Солнца меняется от 249.2 до 206.7 миллионов км в течении года. А в день когда было сделано фото (9 апреля 2021), оно составляло 242.8 (подсмотрено в Stellarium). А соотношение расстояний Марс/Земля было не 1.52, а 1.623. Ошибка в 6.3%, неплохо для разминки.
Ошибка в 1px при измерения полутени от Ingenuity даст погрешность в 1/37 ≈ 3%, а ошибка в 1см в высоте батарейки над тенью (земля под вертолетом не идеально ровная) - погрешность в 2%. Я так-же не исправлял искажения объектива и перспективу, наивно надеясь, что если всё достаточно хорошо центрировать, то ошибки друг-друга скомпенсируют. Дуракам, очевидно, везет.
С количеством света интереснее. У Марса почти нет атмосферы, а вот у Земли есть. И она поглощает заметную часть энергии приходящей от Солнца. Из 1350 Вт/м2, которые получает Земля от Солнца, до поверхности долетает только 1040. А до поверхности Марса ~530 Вт/м2 из 586. Разница в 1.9 раза, а не в 2.3.
2. Вертолеты жужжат
Вертолет, летающий на Марсе, работает на солнечной батарейке, 18650 аккумуляторах, процессоре от смартфона и камерах от Raspberry Pi. Ну разве не потрясающе? Смотрите, как летает:
И на видео даже слышно жужжание винтов! Perseverance, снимающий видео, смотрит на пропеллеры сборку (т.е. находится примерно в плоскости вращения), а значит в спектре звука должна быть очень заметна Blade Passage Frequency. Этот компонент зависит от скорости вращения винта и количества лопастей, а его главная гармоника:
Где n - количество лопастей пропеллера, RPM - обороты в минуту.
Можно собрать пропеллер и проверить как должна выглядеть BPF. Хватаем моторчик от мелкого квадрика и винт от него же. За неимением референсного тахометра, собираем его из спичек и желудей: светодиод воткнутый в микрофонный вход компа и фонарик.
Для получения спектра берем первое попавшееся по запросу «microphone FFT online»
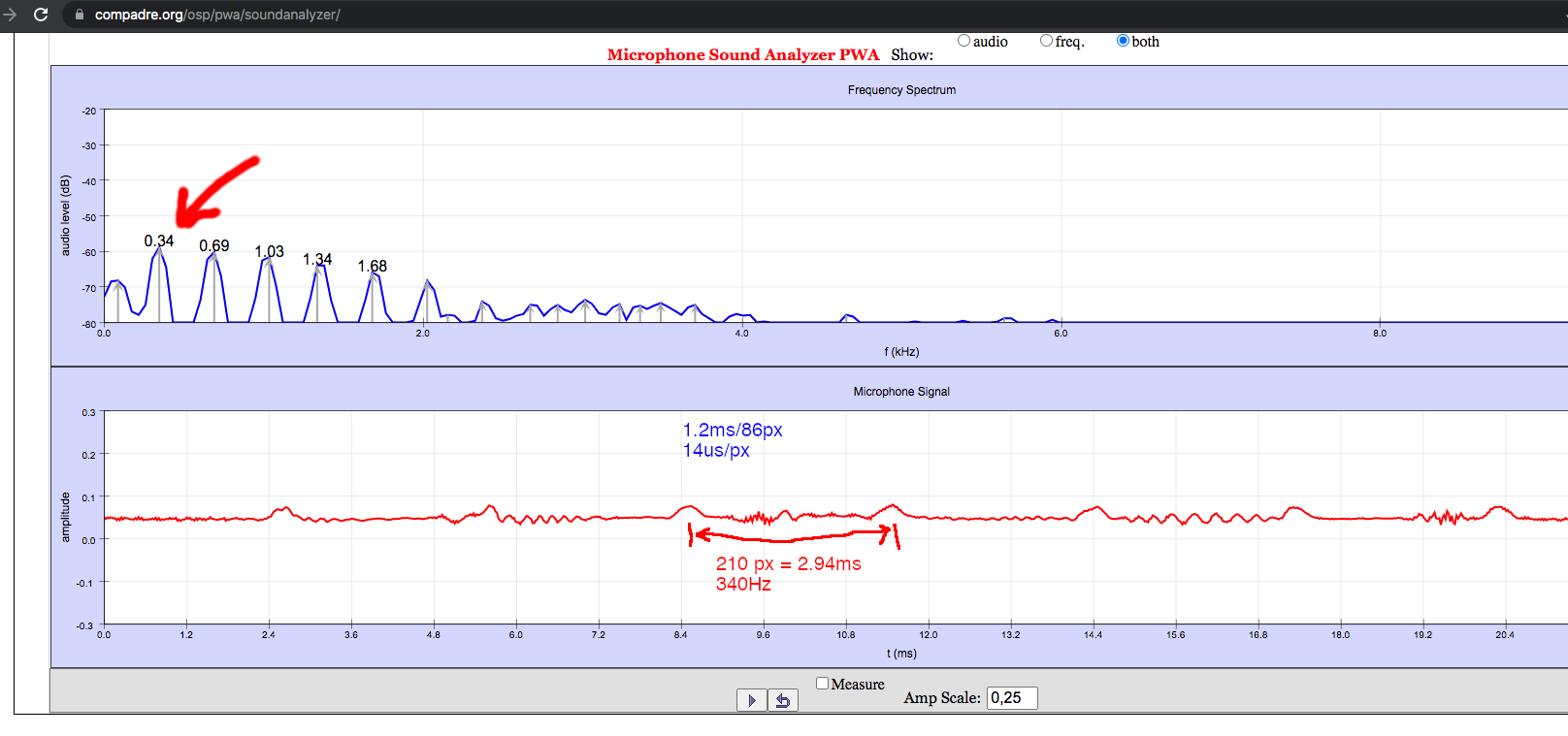
Тени от лопастей проходят мимо светодиода каждые 2.94ms, перекрывая поток света от фонарика, что вызывает изменение фотоэлектрического тока, и уровня сигнала на микрофонном входе. За каждый оборот мимо датчика проходят обе лопасти, так что период вращения винта получается 6ms. А обороты — 10'000 RPM.
Вооружившись этим знанием, берем приложение-спектроанализатор и смотрим на спектр пропеллера:
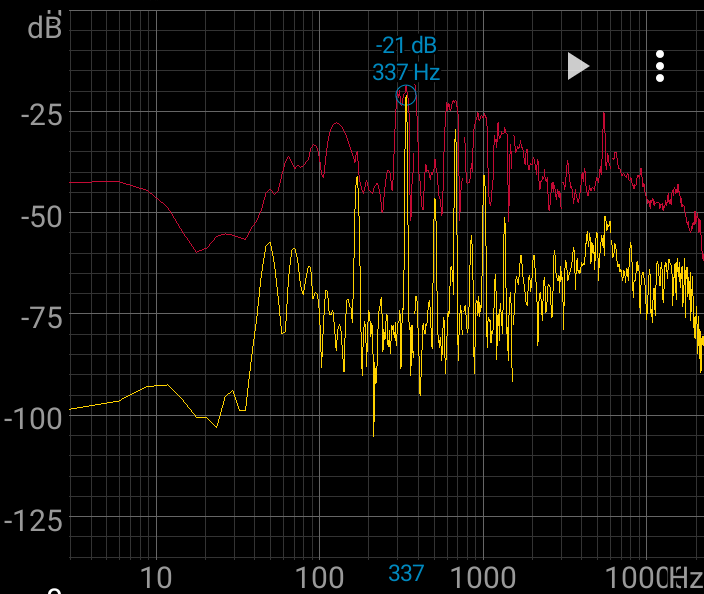
337Гц — та-самая BPF, и разные её гармоники. Убедившись, что всё сходится, посмотрим на BPF вертолета.
Качаем видео, пихаем его в ffmpeg:
ffmpeg -i ./6015_20210507_HelicopterFliesOnMars-1280.m4v \
-lavfi showspectrumpic=s=3000x3000:fscale=log spectrogram.jpg
Картинка получается возмутительно большой, но зато разрешение по частоте и времени позволяет всё разглядеть.
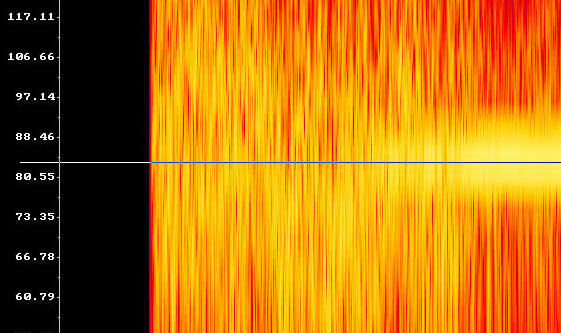
Видно, что пик находится примерно на 84Гц.
Но у ведь Ingenuity не простой винт, а два соосных. Это 2 лопасти или 4?
Не совсем очевидно, но 2. Можно представить себе два пропеллера вращающиеся с одинаковой (иначе вертолет закрутит) скоростью: оба будут шуметь на одной частоте. И как их шум не складывай, ничего кроме громкости меняться не будет.
А можно собрать модель соосного пропеллера из двух обычных и проверить:

Моторы соединены вместе, но повернуты лицом друг к другу, так что винты вращаются в противоположные стороны. RPM (измеренный всё тем-же светодиодом) получился примерно 6000 у каждого.
А спектры шума выглядят вот так:

Пик на ~200Гц как раз соответствует BPF1 для двухлопастного винта на 6000RPM. Обратите внимание что пик двойной — обороты у винтов всё-же немного различаются, и BPF тоже.
А если слушать винты сверху, BPF1 уже не так заметна:

В видео гораздо меньше гармоник BPF. Потому, что звук отфильтровали, заглушив всё лишнее. Но если присмотреться, на спектрограмме видны остатки высших гармоник:

BPF1 на ~84Гц, а значит пропеллеры вращаются примерно на 60*(84/2) = 2520RPM.
Фраза «You can also hear the sound change as the helicopter leaves the area and then returns. That’s called the Doppler effect» которая появляется в видео, меня очень расстроила, потому что я никакого Доплера не слышал. Придется прибегнуть к помощи Машины.
2.2 Эффект Доплера
Вытащим звук из видео в WAV и скормим его numpy. Тон BPF самый громкий (спасибо неизвестному звукорежиссеру из JPL), поэтому мы можем просто выбирать самый высокий пик на FFT и, двигаясь по файлу скользящим окном, построить график его частоты по времени.
Важно выбрать достаточно большое окно, чтобы получить хорошее разрешение по частоте. Если мы хотим (а мы хотим!) разрешение в 0.1Гц, окно должно быть 1/0.1 = 10 секунд.
Почему 10?
Представьте что у вас есть запись длительностью 1 сек, в которой только одна частота. Пусть будет 10Гц. Вы можете посчитать сколько периодов помещается в 1 секунду - 10 штук.
Если частота будет 11Гц, вы насчитаете 11 периодов. Но вот если она будет 10.5Гц, вы уже не сможете уверенно сказать количество. У FFT такие-же проблемы.
Разрешение по частоте определяется как Fs/N где Fs это частота дискретизации, а N количество семплов в выборке. Или, если выборка задана в секундах, как 1/T.
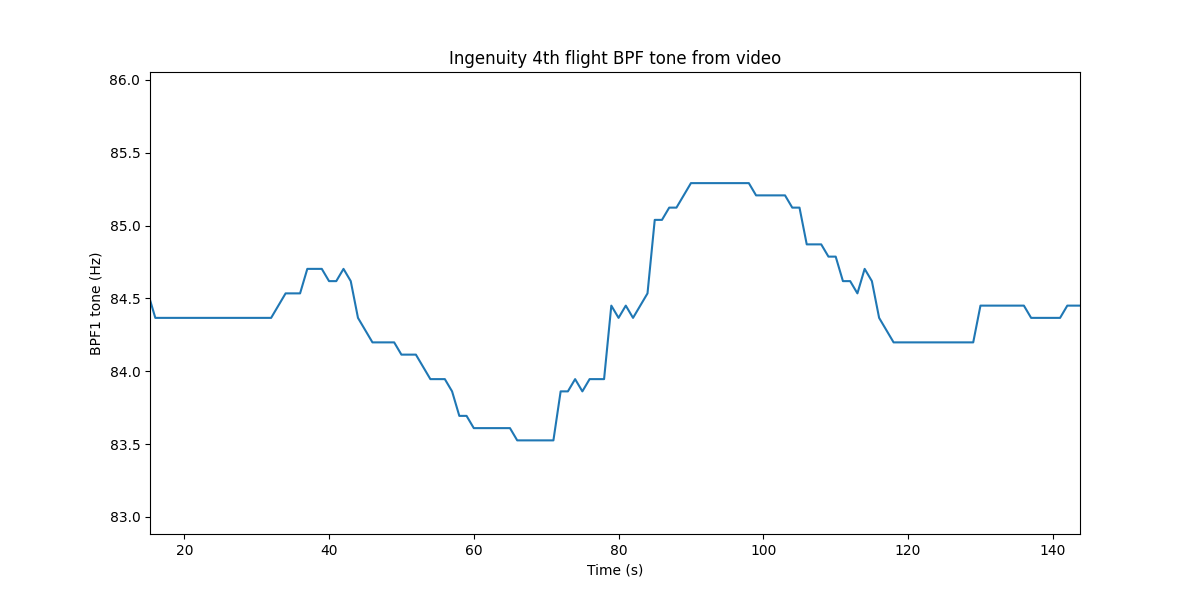
Максимальный сдвиг частоты от центра ~1Гц, или 1.2% от 84Гц. Гугл сообщает что человек различает на слух разницу частот в 0.5%. Ну и пусть различает, а мы посмотрим график:
-
Сразу после взлета вертолет неподвижен. При этом BPF звучит на 84.36Гц, что уточняет обороты до 2531 RPM.
-
Примерно на 32 секунде BPF начинает увеличиваться. А на видео в это же время вертолет начинает разгон. Задержки между видео и звуком не видно, что при скорости звука в 250м/c дает расстояние до вертолета не более 250 метров.
Скорость звука на Марсе
Сильно зависит от времени суток из-за больших перепадов температуры. Она меняется от 216 (при -95°С) до 270 (+5°С) м/c. Вот тут рассказывают как её измерять, стреляя лазером в камни и слушая задержку. Кстати, тем-же самым микрофоном, через который мы слушаем вертолет. 250 м/c я взял практически по-памяти и это отлично совпало со скоростью при текущей погоде. -27°C дают 247м/c.
Раз мы знаем скорость звука, сдвиг частоты можно пересчитать в скорость. Наблюдатель неподвижен, поэтому:
Где v скорость вертолета (вдоль луча зрения), vs скорость звука, f частота для нулевой скорости (84.36Гц), fo - наблюдаемая частота.
При разрешении по частоте в 0.1Гц, разрешение по скорости выходит ~0.3м/c. Неплохо.
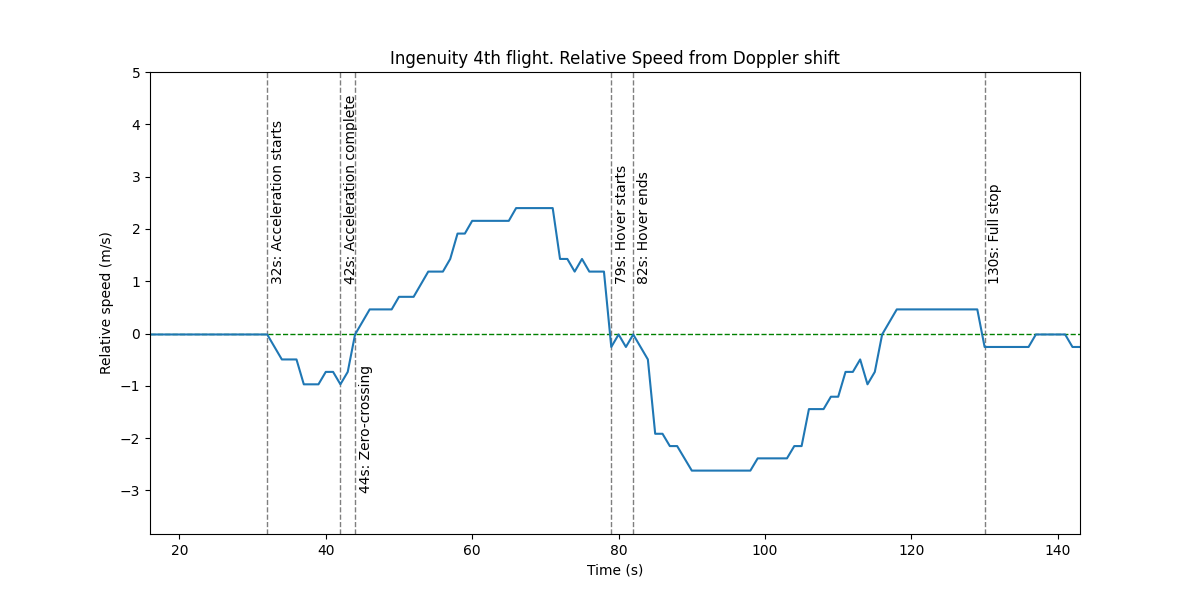
Видно, что график симметричный относительно центра, значит вертолет летал примерно одинаково туда и обратно. В центре есть 3 секунды, когда скорость была нулевой: на взлет и посадку нужно больше, значит он просто потупил в дальней точке и полетел домой.

Относительная скорость в начале отрицательная (он приближается!), а на 44 сек резко переходит через 0 и продолжает расти. Вертолет летел по прямой, поэтому путь должен пролегать примерно так
2.3 С какой скоростью он летал?
На 42й секунде видно, как Ingenuity завершает разгон и возвращается в вертикальное положение. Эффект Доплера дает нам лучевую скорость ~1м/c в этот момент. Скорость в проекции можно оценить взяв два кадра из видео с разницей в пару секунд:

347/2 = 173 пикселя за секунду. Высота от дна корпуса до верхушки вертолета ~36 см, а на картинке ~17.5 пикселей: скорость в проекции 173*(0.36/17.5) = 3.56 м/c.
А полная скорость из этих двух компонентов: 3.7 м/c.
2.4 Можем ли мы уточнить расстояние от ровера до вертолета?
Возьмем два фрейма в начале полета: тот на котором Ingenuity еще не начал разгон, и тот на котором он уже почти вылетел из кадра.

Можно измерить размер вертолета на обоих фреймах (лучше всего измерять высоту от дна корпуса до верхушки) и узнать, что он увеличился примерно с 16.5 до 17.5 пикселей, или на 6%.
Между фреймами прошло 10 секунд, в течении которых вертолет разгонялся, и его максимальная скорость вдоль луча зрения составила ~1м/c. При равномерном ускорении это дает (1/2)*10 = 5 метров на которые вертолет приблизился к камере.
За 5 метров угловой размер вертолета вырос на 6%. Что дает нам 5/0.06 = 83 метра дистанции на момент старта.
Но этот метод очень грубый: Если бы размер изменился не на 1 пиксель, а на 2, дистанция получилась бы 43 метра. Да и лучевая скорость у нас с разрешением 0.3м/c.
Попробуем прикинуть расстояние еще одним способом. Можно сделать очень смелое предположение, что вертолет летает какой-нибудь из сторон ланчбокса вперед, и посмотреть как он ориентирован в начале полета.

3D модельку можно покрутить тут
Выглядит как 22.5°.
А значит,

Разгон начинается в 32 секунды, а в 44 секунды скорость на графике переходит через 0 — в этот момент он летит перпендикулярно лучу зрения. 10 секунд ускорения и 2 секунды полета на 3.7м/с дают 26 метров от начала полета до ближайшей к камере точки. Отсюда,
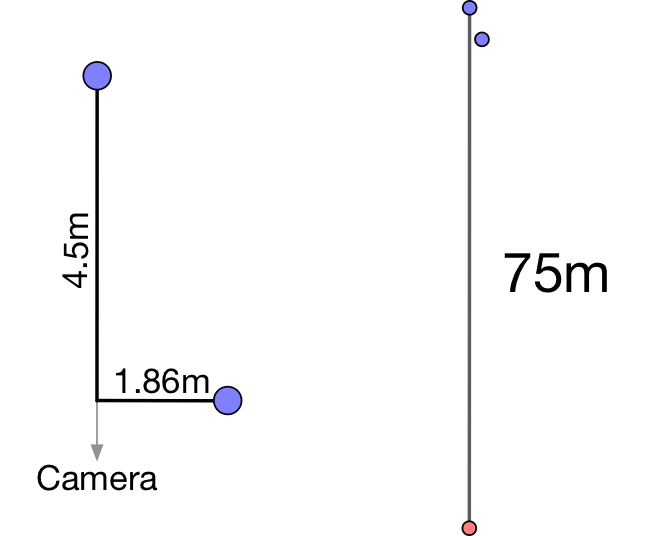
Правда наверняка где-то между, поэтому возьмем среднее от 83 и 68 — 75 метров.
Кстати, можно представить поле зрения камеры: за время пролета вертолета через весь кадр, направление изменилось на 22.5°. Горизонтальный FOV в 24° дает 55мм объектив кроп-факторе 1.5. То есть буквально как китовый 18-55 на камере с APS-C выкрученный на самый большой зум.
2.5 Места взлета и посадки отличаются
Сравним два кадра:

Картинка увеличена в 10 раз, смещение на 85.5 и 5.5 пикселя. Место посадки было правее и ближе, чем место взлета.
Высота вертолета от дна ланчбокса до верхушки - 36см и 16 пикселей на фото, значит он сместился на 85.5*(36/16) = 186 сантиметров вправо в проекции.
5.5 пикселя вниз, дают 12см в проекции. Предположим, что поверхность ровная и плоская, и что высота мачты с камерой на ровере 2 метра. Тогда, смещение по поверхности вдоль луча зрения 0.12*(75/2) = 4.5 метра.

Что дает:
2.6 Как далеко летал Ingenuity?
Мы знаем, что места взлета и посадки различались, поэтому считаем по-отдельности:
По графику видно, что он начал движение в 32сек, а закончил в 79: 47 секунд полета, из которых 20 на разгон и торможение: 273.6+203.6/2 = 134,7 метра для первой части маршрута.
Обратный путь начался на 82 и закончился на 129 секундах, что тоже дает 47 секунд.

Значит, видимое смещение точки посадки вправо вызвано просто углом траектории относительно луча зрения (а может быть, скорости были разными для двух участков пути):
Действительно, arctan(1.86/4.5) ~ 22.5°. А угол a очень мал, потому что длина пути гораздо больше расстояния между точками.
Суммарная дальность полета получилась 269.4 метра.
2.7 Теперь можно нарисовать план полета
Мы знаем все нужные расстояния и углы:

2.8 Симуляция жужжания
Перед тем как сравнивать всё это безобразие с реальными данными, маленькое отступление. Спектрограмма выглядит страшно, на ней видны порывы ветра, которые почти заглушают гудение мотора. Разрешение в 0.3м/c и окно в 10 секунд не внушают доверия. Можем ли мы вообще говорить о точности в 1 секунду, когда окно такое большое?
Давайте набросаем симулятор жужжащего вертолета. Отсюда можно взять относительные координаты ровера, и точек в которых садился вертолет:

Смотрим координаты на скриншоте и измеряем полоску с масштабом:
meters_per_pixel = 50/167
rover = np.array([740, 274])*meters_per_pixel
heli_p1 = np.array([501,209])*meters_per_pixel
heli_p2 = np.array([573, 653])*meters_per_pixel
heli_p3 = np.array([520, 210])*meters_per_pixelДобавим разные параметры по-вкусу:
dt = 0.1
hover_time_at_liftoff = 10
hover_time_at_p2 = 3
hover_time_at_landing = 10
accel_time = 10
max_speed = 3.7
center_freq = 84.36
speed_of_sound = 250И составим план полета:
hover(hover_time_at_liftoff) # Hovering at p1
set_target(heli_p2)
accelerate(max_speed, accel_time) # Accelerating at p1
free_flight(accel_time) # Flying to p2
decelerate(0, accel_time) # Decelerating at p2
hover(hover_time_at_p2) # Hovering at p2
set_target(heli_p3) # Going home
accelerate(max_speed, accel_time) # Accelerating at p2
free_flight(accel_time) # Flying to p3
decelerate(0, accel_time) # Decelerating at p3
hover(hover_time_at_landing) # Hovering at p3Чо творится?
Каждая из функций апдейтит положение вертолета и, с шагом dt заполняет массив значениями BPF с учетом скорости.
hover(t) не меняет скорость и завершается через t секунд
set_target(p) меняет вектор направления вертолета, чтобы он двигался к p
accelerate(s, t) увеличивает скорость до s в течение t секунд
free_flight(t) сохраняет текущую скорость и завершается, когда время до цели будет < t
decelerate(t) - как accelerate только с другим знаком и s = 0.
Получилась вот такая красота:

Выглядит точь-в-точь как график, полученный из видео. Амплитуды и тайминги похожи. Чуть ниже будет картинка с наложением одного на другое, а пока можно поиграться с симулятором и посмотреть, что изменится при разных параметрах полета.
Допустим, дальняя точка была расположена на том-же удалении, но так, что вертолет улетает под углом 10° (а не 22.5°) к проекции камеры:
heli_p2 = np.array([457, 653, 5])*meters_per_pixel
Скорость приближения в начале и конце полета гораздо ниже, а сдвиг частоты всего 0.05Гц. Мы бы даже не заметили этого на графике.
Теперь сложнее. Пусть вертолет, после того как вылетит из кадра, поворачивает немного в сторону, а потом тем-же путем возвращается обратно:
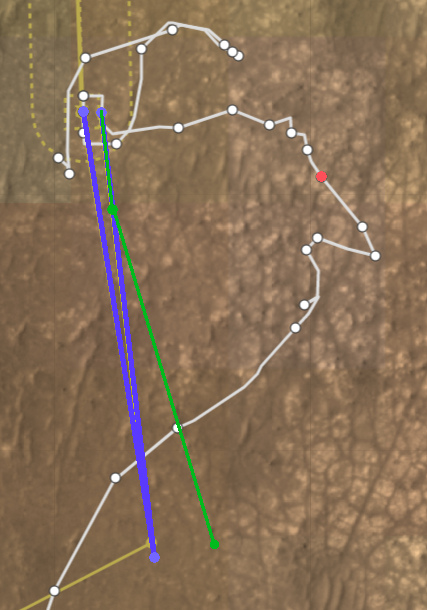
Получатся так:

Видно момент, когда из-за смены направления резко меняется относительная скорость. Я сделал поворот моментальным, в реальности переход был-бы более гладким, но с такой-же амплитудой. Не уверен что его было бы видно на нашем графике, но более резкий поворот точно был-бы заметен.
2.9 Ошибки?
1) Реальное значение RPM было 2537 а не 2531. Ошибка около 0.2% или 0.2Гц для BPF. Вполне близко к пределу точности измерений.
3) Скорость полета, по данным в википедии, 3.5м/c, а не 3.7м/c. Ошибка в 6%. Неплохо, учитывая то, как мы её измеряли.
Можно наложить график симуляции на реальные данные и сравнить:

Видно что симуляция (со скоростью 3.7м/с) немного спешит.
Еще стоит заметить, что в симуляции я не учел задержку звука. Но она составляла всего пол секунды в дальней точке:
Rover-Heli dist @ start: 74.2 meters, sound lag 0.30 sec
Rover-Heli dist max: 124.0 meters, sound lag 0.50 sec4) Расстояние от камеры до Ingenuity на старте, измеренное по карте, получилось 74 метра, а не 75. 1.3% и наглядное подтверждение того, что измерять вещи разными способами и усреднять полученное — полезно. Но вообще, скорее повезло.
6) Дальность полета, по данным из википедии, составляла 268.5 метров в обе стороны. У нас вышло 269.4 метра. Ошибка в 0.3%. На удивление, гораздо меньше ошибки в скорости. Видимо какие-то из предположений (одинаковое время разгона-торможения, равномерное ускорение, одинаковая длина путей) оказались ложными, но ошибки скомпенсировали друг-друга.
5,7) Можно наложить наш план полета на реальную карту:

Я выбрал в качестве опорной точки положение марсохода, а в качестве опорного направления — линию между ним и точкой старта. Совпало хорошо. Чуть-чуть ошиблись в точке посадки, и на пару градусов по направлению. В обоих случаях мы разглядывали 2,5 пикселя, так что ошибки можно понять.
2.10 Всякое
Последняя интересная вещь в видео — посадка вертолета. Коснувшись земли, он немного подпрыгивает и окончательно приземляется на 136 секунде. А на спектрограмме из ffmpeg виден момент когда винт начинает резко сбрасывать обороты:
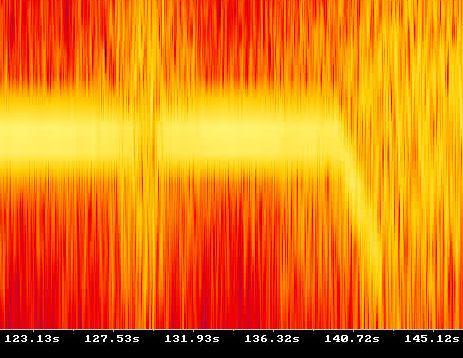
Разница между приземлением и отключением пропеллера 3 секунды. Ingenuity, коснувшись песка, медленно и осторожно уменьшает угол атаки винтов, постепенно увеличивая нагрузку на грунт. И только когда убедится, что опора надежная — выключает моторы. А в эти 3 секунды он готов взлететь и повторить попытку, если датчики заметят что-то неладное.
А вот видео, где вся движуха собрана на один экран:
Вертолеты на Марсе действительно жужжат, и жужжат занимательно.
2.11 Оффтоп 1: Пассивный Доплер-радар
Вернемся к симулятору жужжания:
meters_per_pixel=1.0
rover = np.array([0, 0, 0])*meters_per_pixel
heli_p1 = np.array([5000.0, 200, 200])*meters_per_pixel
heli_p2 = np.array([-3000.0, 200, 200])*meters_per_pixel
. . .
set_target(heli_p2)
accelerate(200, 1)
free_flight(1)Тут вертолет быстро разгоняется до 200 метров в секунду, и пролетает мимо ровера:

Скажем, мы хотим по этой записи найти скорость вертолета, но не знаем даже BPF для нулевой скорости.
Но лучевая скорость становится нулевой в тот момент, когда он пролетает ближайшую точку. И ее можно найти, если принять, что скорости до и после пролета были одинаковыми, но с разным знаком:
Действительно, если взять f1 = 417Гц, а f2 = 45Гц (я взял точки в противоположных концах графика), получается 81.2 Гц. Ошибка в 2.5%, но это не так важно, потому что:
v1 = 250*(81.2/417-1) = -201.3 m/s
v2 = 250*(81.2/45-1) = 201.11 m/s
В тех точках где я измерял частоты, вертолет находился достаточно далеко (порядка 3км), так что я пренебрег поправкой на направление. Но если вам интересно, на 3км угол к лучу зрения получается 5.5°, а cos(5.5°) = 0.995. Погоды не делает.
Ошибка получилась меньше 0.5%. Круто? Попробуем в деле:
Возьмем видео с самым красивым самолетом. 20и-метровый кусок металла с аэродинамикой шлакоблока и радарной сигнатурой маленькой птички, не падающий с неба только благодаря хитрой управляющей электронике. Да, я про F-117:
Можем ли мы измерить его скорость?
Посмотрим на спектрограмму:

Кривая перехода сразу бросается в глаза. Возьмем две частоты и посчитаем:

Частота для нулевой скорости получилась 422Гц.
А скорость вдоль луча зрения в начале видео:
350*(422/898 - 1) = -185.5 м/c
Но летел он не прямо на камеру, а под углом градусов в 15. Так что реальная скорость:
-185.5/cos(15) = -192м/c
Какая была на самом деле? К сожалению видео об этом умалчивает, поэтому возьмем два соседних фрейма, где самолет летит на фоне гор, совместим и измерим:

F-117 в длину 20.1 метр. Но это до края хвостового оперения. А до заднего края корпуса — 17.1 метр. Скорость получается 43*(17.1/110)*30 ≈ 200 м/с. Мы ошиблись на 4%. Наверняка из-за кривой оценки угла, или скорости по фреймам.
2.12 Оффтоп 2: Марсианская аэродинамика
Как известно, у летательного аппарата два врага: сила тяжести и сопротивление атмосферы. Мне было интересно оценить, насколько на вертолет влияет второе (может ему и правда надо летать углом вперед?).
Где Fd сила сопротивления атмосферы, p - плотность, v - скорость вертолета, A - площадь сечения, а k - аэродинамический коэффициент.
-
Плотность атмосферы на Марсе около 0.02 kg/m3
-
Скорость 3.5м/c
-
k считать сложно, скажем, вертолет имеет форму куба (k = 1).
Осталось узнать площадь сечения. Это просто. Открываем 3д модельку и крутим ее до тех пор пока не будет похоже на на вертолет летящий прямо на нас:
Закрашиваем тень, потому что она темнее чем коробка вертолета, и двигаем белый маркер на гистограмме влево, чтобы он стал левее пика светлого фона:
Теперь гистограмма показывает количество пикселей темнее фона. Что, фактически, площадь сечения вертолета с этого ракурса. Правда она в пикселях. Но высота от дна до верхушки тут 100 пикселей, что дает 3.6мм на пиксель. Значит один пиксель это 13мм2, а 8051 пикселей - 104341мм2. Или 0.1м2.
(0.023.5^20.5*0.1)/2 = 0.01225 Ньютона
F = m*a
0.01225 = 1.8*a
a = 0.007м/с2
То-есть, за 27 секунд полета вертолет теряет всего 0.2 м/c скорости.
3. Вертолеты не отбрасывают тени
Вернемся к заглавной картинке (наконец-то!)

Четыре вещи на ней выглядят подозрительно:
-
Вертолет явно в воздухе, значит лопасти вращаются на 2500 RPM, а выглядят они очень четкими. Какая же там должна быть выдержка, диафрагма и ISO чтобы получить такую картинку с хорошей экспозицией и не утонуть в шумах и красивом бокэ?
-
Лопасти кажутся полупрозрачными. Странности добавляет и тень от ноги поверх тени пропеллера, которая прозрачной не выглядит.
-
Сверху лопасти более темные, чем снизу.
-
На переднем (более прямом) крае лопасти тень выглядит темнее. Причем на некоторых фото это заметно, а на других — нет:

Что за камера помогает Ingenuity ориентироваться на местности? Это OV7251. 640х480, отсутствие фильтра Байера, глобальный электронный затвор и до 120FPS в максимальном разрешении. Размер матрицы 1/7.5", а размер пикселя 3х3мкм. Эта камера бывает в двух исполнениях — для видимого света (с hotmirror, который отсекает ИК излучение), и для ближнего ИК (с полосовым фильтром на 830нм).
Надо заметить, что мне так и не удалось найти (или понять по фото) какая из двух версий камеры используется на Марсе. Далее я буду предполагать что обычная.
3.1 Гадание по фотографии
Попробуем оценить выдержку. Ищем какое-нибудь прямое место на лопасти и измеряем ширину полутени. Заодно, измеряем и ширину полутени от солнечной батарейки.
15 пикселей для винта и 10 пикселей для батарейки. Значит винт смазался вращением на 5 пикселей, что на таком расстоянии от оси вращения дает 1.5°. Но мы не учли искажения оптики: вещи на поверхности, ближе к краю кадра выглядят меньше, чем на самом деле. Пусть будет угол в ~2°, или 1/180 от полной окружности. Полную окружность лопасть проходит за 60000/2500RPM = 24мс, а 1/180 за 133мкс. Это и есть длительность выдержки. Ну или 1/7500, если вы фотограф.
Ошибка на 0.5° при измерении угла, дает примерно 33мкс разницы. К примеру если бы угол был в 1.5°, выдержка получилась бы 100мкс или 1/10000.
Теперь ISO. Хоть светочувствительность по ISO-12232 и не используется в этих камерах, её хорошо знать для сравнения с обычными фотоаппаратами. Когда камеры были большими, а экспонометры отдельными и дорогими, люди пользовались правилом «Sunny 16» чтобы подбирать выдержку. Правило гласит:
On a sunny day set aperture to f/16 and shutter speed to the [reciprocal of the] ISO film speed for a subject in direct sunlight
Сделаем поправку на то, что Марс дальше от Солнца и на него попадает в 2 раза меньше света. Делим 16 на и получаем Mars 11 rule. С диафрагмой f/11 и выдержкой 1/7500 матрице нужна будет чувствительность ISO 7500 чтобы получить нормальную экспозицию. Звучит как высокое и шумное ISO, но подождите.
Размер пикселя слишком мал, чтобы позволить диафрагму f/11: дифракционный предел размажет картинку.
Где d - минимальный размер пятна, N - диафрагма, а λ - длина волны света.
При диафрагме f/11 и λ = 550нм, d получается ~15мкм, целых 5 пикселей (размер пикселя у OV7251 - 3мкм).
Но на кадрах с камеры можно разглядеть отдельные детали в пару пикселей размером, значит d не сильно больше размера пикселя. Пусть будет как-раз 3мкм. Тогда:
N = 2.23
Чтобы дифракция не влияла на картинку, диаметр диафрагмы нужно увеличить в 11/2.23 = 5 раз. Поток света увеличится в = 25 раз, и ISO нужно уменьшить до 7500/25 = ISO 300. Хорошее, низкое ISO. И совсем не шумное.
Но хватит ли, при такой большой диафрагме, глубины резкости, чтобы без автофокуса снимать объекты на расстоянии от 15 сантиметров (когда вертолет приземлился) до десятков метров? Мы можем прикинуть гиперфокальное расстояние. Это расстояние H от камеры до точки фокуса, при котором в поле резкости попадает всё от H/2 до бесконечности:
Где H - гиперфокальное расстояние, f - фокусное расстояние объектива, N - диафрагменное число, а c - диаметр круга нерезкости. Круг нерезкости имеет тот-же смысл что и пятно в дифракционном пределе: мы не хотим чтобы он был больше пикселя.
Не хватает фокусного расстояния объектива. Но мы знаем, что размер матрицы 1/7.5", а угол зрения сильно больше 90° но меньше 180°. Пусть будет середина — 135°. Из справочных табличек (или опыта общения с зеркалками), можно узнать что для full frame матрицы угол в 130° получается при 10мм объективе. Диагональ full frame 1.7", а значит кроп-фактор для 1/7.5" матрицы 12.75. Фокусное расстояние получается 10/12.75 = 0.8мм.
Гиперфокальное расстояние:
H = 0.8^2/(2.23*0.003) = 95.6мм
0.003 - это 3мкм, размер круга нерезкости
Если сфокусировать объектив на 95мм, то резким будет всё от 47мм до бесконечности. Так что глубины резкости хватит с запасом.
Можно поискать модули с этой матрицей чтобы убедиться, что мы не сильно ошиблись. Вот модуль с фокусным расстоянием 1.3мм (и углом зрения в 86°), диафрагмой f/2.2 и фиксированным фокусом от 65mm до бесконечности. В целом сходится.
1/7500", ISO300, диафрагма f/2.2 и объектив с фокусным расстоянием 0.8mm. Странная конфигурация, если вы привыкли к большой фототехнике.
А если бы камера работала в ИК (λ = 850нм), то получилось бы: ISO120, диафрагма f/1.4 и гиперфокальное расстояние в 15 сантиметров.
3.2 Прозрачные лопасти
У этой части проблема с экспериментальными данными: проснувшись однажды утром после беспокойного сна, я обнаружил, что в доме нет ни одной камеры с глобальным электронным затвором, годной для переделки в ИК. Да и негодных нет. В конце мы компенсируем недостаток реальности численным моделированием (отвратительный код на питоне, да).
3.3 Потому, что прозрачные.
Самый очевидный вариант, объясняющий полупрозрачность теней, который приводят в каждом втором обсуждении этих фотографий: лопасти выглядят прозрачными потому-что они прозрачные. Логично.
Ведь OV7251 может работать в диапазоне ближнего ИК, где вещи выглядят неожиданно. Знаменитые примеры:
-
Тёмное, почти черное, небо. И чем дальше в ИК — тем темнее.
-
Яркие листья на деревьях, благодаря эффекту Вуда (не от слова "wood", а от слова Robert Wood)
-
Прозрачность разных пластиков и красителей
Может быть и с лопастями так-же? Лопасти у Ingenuity карбоновые, и это хорошо: у меня есть такие-же. В этот раз не придется даже думать, хватаем пропеллер и смотрим на тень от солнца:

Рядом для сравнения светофильтр, прозрачный в ИК, hotmirror непрозрачный в ИК* но прозрачный в видимом свете и кусок дискеты. А снизу то-же самое, но в видимом диапазоне.
Светлое пятно под hotmirror не от того, что оно пропускает ИК, а от того, что отражает вниз свет который попадает на его нижнюю сторону с яркой бумаги. Смотрите, как оно отражает держалку с круглым фильтром. Потому и "mirror".
Тень от пропеллера совершенно такой-же яркости, как тень от мотора рядом:

3.4 Оффтоп 3: Инфракрасная фотография для бедных
А вот тень от дискеты чуть прозрачнее тени от держалки:

Дискета пропускает очень небольшое количество ИК и красного света. Она сойдет за lowpass-фильтр, если вы хотите попробовать ИК фотографию, а покупать нормальный фильтр не хотите.
Вот пара фоток на дискету:


Откуда берутся цвета на инфракрасных фото? Посмотрите на спектральную чувствительность фильтра Байера:

В серой части (как раз там работает ИК фотография) разные каналы всё еще дают разные значения, а значит есть цветовой контраст. Но чем дальше в ИК, тем меньше их различия. Начиная с 850нм, все каналы практически одинаковы. И действительно, чем дальше граница среза у lowpass фильтра, тем меньше насыщенность картинки:

Конечно, производителей не волнуют характеристики фильтра Байера в ИК, поэтому цвета заметно меняются от камеры к камере.
В общем, карбоновые пропеллеры не относятся к вещам, предательски изменчивым в ИК. Приятно знать.
Ну и чтобы окончательно развеять сомнения, можно посмотреть вот эту фотографию:

Лопасти тут не вращаются и совершенно не прозрачны. А значит, дело в движении и таймингах.
3.5 Лопасти перемещаются во времени!
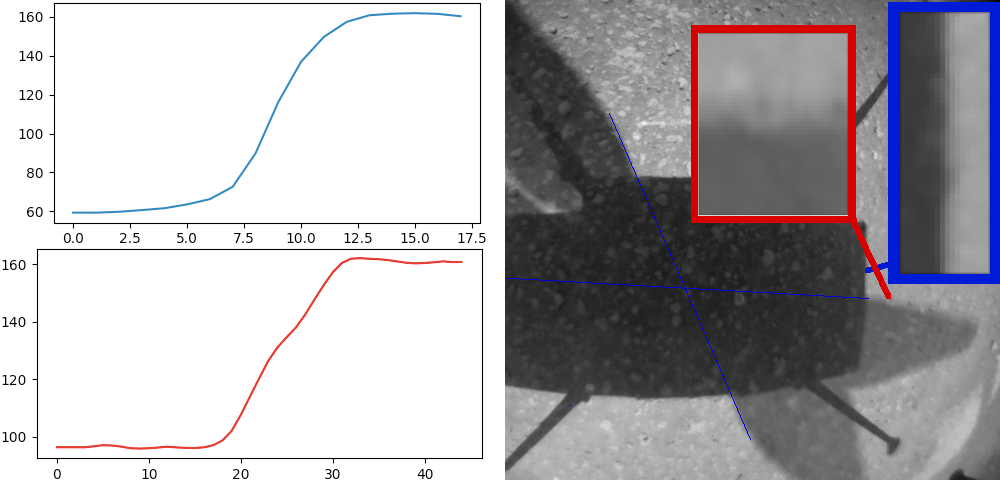
Помните эффект, возникающий при фотографировании со вспышкой чего-то шустрого? Рассмотрим фотографию комара:

Крылья получились четкими, но вокруг них смазанный след, потому что длительность вспышки гораздо меньше длительности выдержки. Но след полупрозрачный, потому что вспышка яркая и хорошо подсветила деревья.
Можно повторить то-же самое с пропеллером:

Такой-же эффект, как на фото Ingenuity! Но ведь у камеры вертолета нет вспышки, ему светит солнце. Откуда этот эффект получается у него?
Ответ скрывается в устройстве самой матрицы:
Данные считываются с CMOS матрицы построчно. Контроллер выбирает одну из строк, и АЦП через мультиплексор по-очереди измеряет заряд на пикселях. Затем следующую.
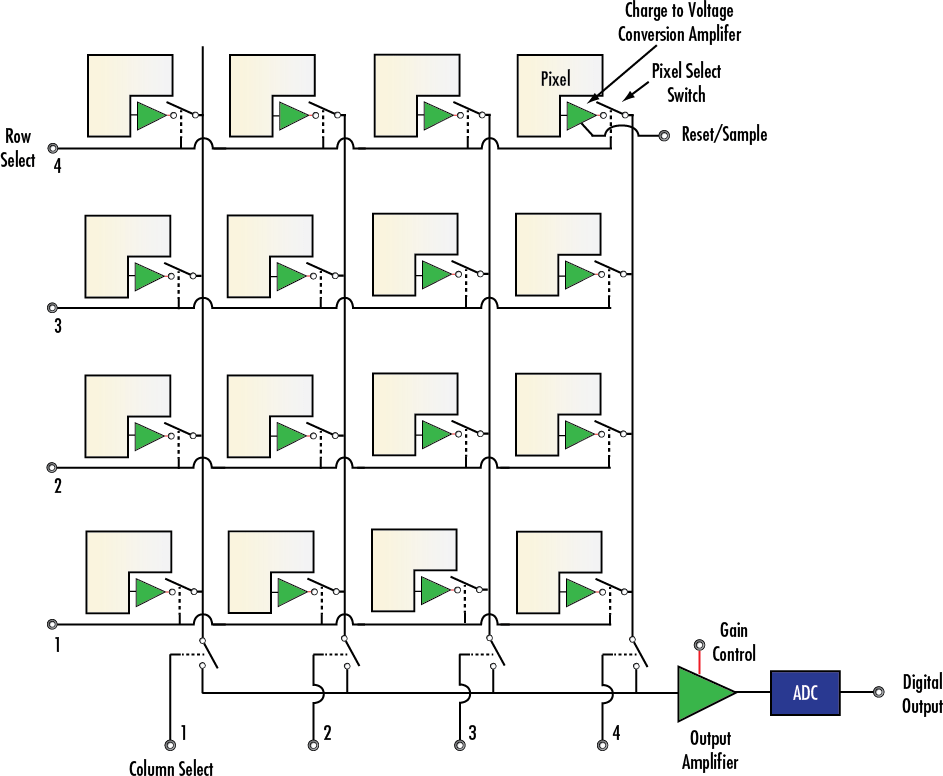
Процесс длится порядка миллисекунд, что сравнимо с длительностью выдержки или даже больше. Поэтому в классических цифровых фотокамерах, по завершении экспозиции матрица прикрывается от света механическим затвором.
А если механического затвора нет, можно экспонировать и считывать строки по-отдельности. Тогда у вас не будет проблемы с тем, что другие строки ждут своей очереди под светом. Но будут другие проблемы: да, мы говорим о rolling shutter. Строки экспонируются в разное время, и объекты в кадре могут успеть переместиться.
Более сложной и дорогой альтернативой rolling shutter является global shutter. Тут вы экспонируете всю матрицу сразу, но по завершении экспозиции перемещаете накопленный пикселем заряд в защищенную от света область, называемую storage node.
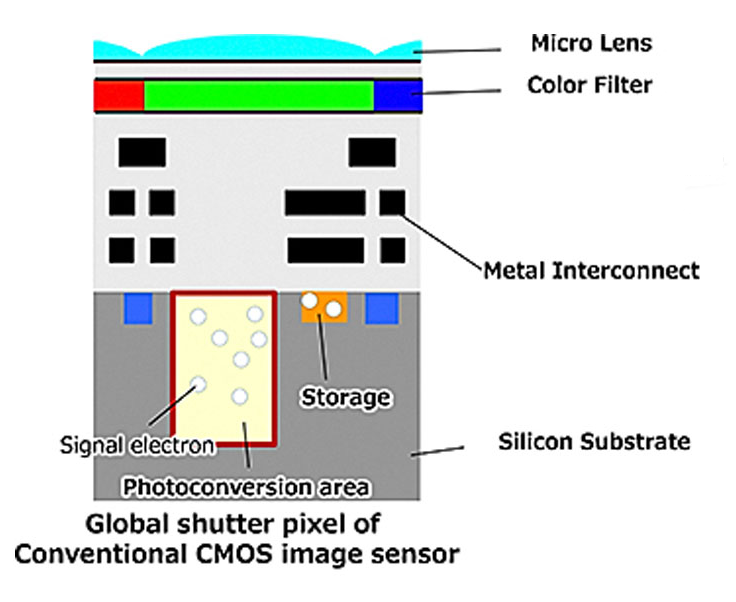
Она маленькая, находится вне фокуса микролинзы и прикрыта от света линиями управляющих сигналов, а то и отдельной крышечкой из металлизации. Перемещение зарядов со всех пикселей происходит одновременно, и уже после этого вы неспешно считываете заряды. Как-будто у вас механический затвор.
Вот только он не механический и не 100% эффективный. Крышка на storage node не может быть значительно больше самой storage node, и свет может под неё проникать за счет дифракции на всякой фигне вокруг. А еще электроны, выбитые фотонами, попавшими мимо фотодиода, могут долететь до storage node.

Эта нежелательная засветка при "закрытом" затворе называется Parasitic Light Sensitivity (PLS) и ужасно всех бесит уже много лет.
Пиксели будут засвечиваться, пока идет чтение, причем те которые считываются последними — засветятся больше всех. А если между завершением экспозиции и началом чтения есть пауза, то пиксели будут засвечиваться и в это время, но равномерно.
PLS, в различных статьях, как и другие специфичные вещи, выражается в чем угодно в зависимости от давности статьи и фазы луны на момент написания: Сначала это называли Shutter Efficiency и измеряли в процентах. 99% означает что закрытый затвор пропускает 1% света.
Когда отличать 99.98% от 99.99% стало слишком тяжело, ввели термин PLS ratio. Например 1/10000 означает что закрытый затвор пропускает в 10000 раз меньше света чем открытый. Иногда указывают 1/PLS, чтобы не писать "1/".
Но так-как писать 4-5 нулей довольно утомительно, PLS выражается еще и в децибелах, например -40dB = 1/10000. Или 1/PLS, чтобы не писать у децибелов минус.
Я же пойду еще дальше и буду говорить PLS, имея ввиду 1/PLS.
3.6 Попробуем оценить PLS у нашей камеры
Сколько времени занимает считывание кадра с матрицы? В даташите этого не написано, но можно примерно прикинуть из таймингов камеры:
На странице 31 указан System Clock в 48MHz. А на 20й странице — тайминги MIPI.

Полное время передачи одного фрейма (1) занимает 478848 тактов SysClock, или 10мс (что как раз дает 100 FPS). Но из этого времени только 445056 тактов (9.3мс), занимает передача самого фрейма. Потому что тайминги (2), (3), (5), (7) и (9) — не относятся к передаче полезных данных.
Можно убедиться, поделив 445056 на 928 (период передачи одного пакета) и получив 480 — количество строк сенсора. Значит в каждом пакете одна строка. А то, что из 928 тактов больше половины — пауза между пакетами, говорит о том, что строки действительно оцифровываются по-ходу передачи. Так что ~9.3мс это время чтения сенсора.
Выдержка была ~133мкс, а значит, время чтения в 70 раз больше выдержки.
Можно вернуться к веселым экспериментам. Возьмем две фотографии тени от пропеллера: неподвижного и размазанного вращением.

Скомбинируем их в режиме Addition (по-пиксельное сложение яркости) и сравним с фотографией, где вертолет летит высоко над землей. Лопасти находятся примерно в центре кадра, так что отношение чтение/выдержка будет ~35.
Скажем, что фото с неподвижным винтом это идеальный затвор. А фото с размазанным - эффект от PLS. Тогда, если бы PLS была ровно 35, то простое сложение кадров дало бы такой-же эффект как у вертолета (экспозиция размытого кадра в 35 раз дольше, но сенсор в это время в 35 раз менее чувствительный):

Похоже? Да, но слишком прозрачно.
Покрутим экспозицию для слоя с размазанным пропеллером.
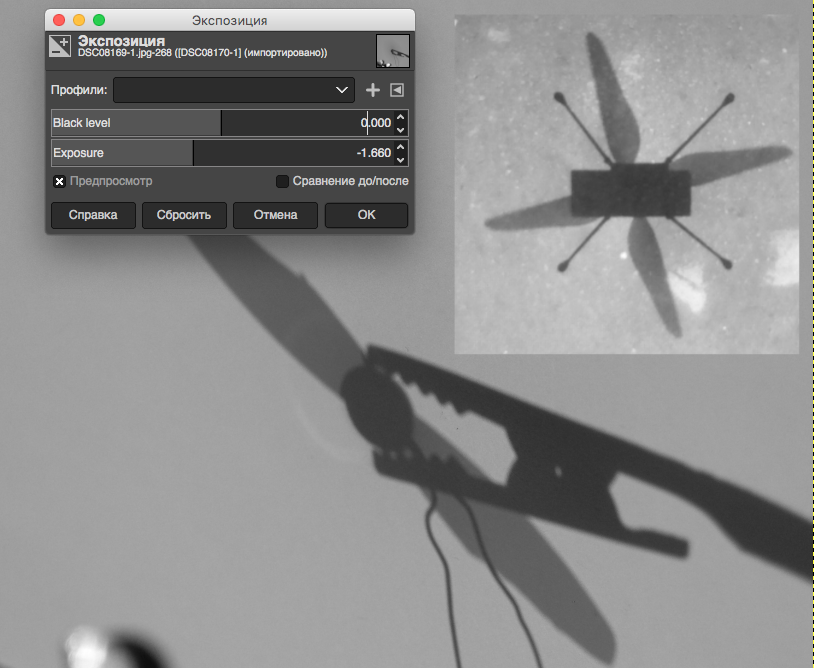
Ну вот, 1.66 ступени вниз и выглядит гораздо лучше. Это эквивалентно уменьшению светочувствительности в 2^1.66 = 3.17 раза. Значит, PLS примерно 35*3.17 ≈ 111.
Такое значение PLS кажется очень плохим по современным меркам. В работах 2018 и 2019 годов приводятся цифры на два порядка лучше для пикселей того-же размера.
Даже в пресс-релизе 2019 года, где Omnivision анонсирует новую версию этой камеры - OV7251-1B, заявлена эффективность в 99.96% (PLS = 2500).
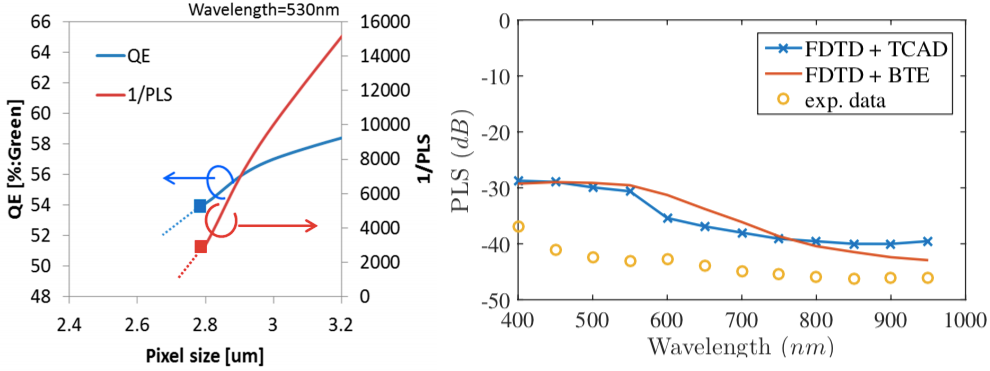
Но на всяческих видео и пресс-конференциях команда Ingenuity рассказывала, что работа над вертолетом велась 5-6 лет. В 2014 году вышел Snapdragon 801 который стоит в Ingenuity и моем телефоне, в 2014-же году вышла первая версия OV7251. И графики от 2013 показывают, что в те давние времена, PLS была довольно печальной:

Обратите внимание, что это график для пикселя размером 3.75мкм, а на OV7251 — 3мкм. И PLS очень стремительно ухудшается с уменьшением размера пикселя: примерно в 5 раз на 10% уменьшения размера. Между 3.75 и 3 — 20% разницы, что дает ухудшение в 10 раз и PLS порядка 100. Сходится.
3.7 Откуда на фото градиент яркости?

Потому, что разные строки ждут очереди на считывание разное время. Верхняя строка считывается первой, и PLS на неё не влияет: верхняя часть кадра самая темная. Нижняя строка считывается последней, а до этого засвечивается все 9.3мс. Средняя — в течении 4.65мс.
Попробуем получить PLS еще одним способом (с расстоянием до ровера ведь сработало!). Возьмем все фотографии c навигационной камеры и слепим из них одну:
convert -evaluate-sequence mean ./HELI_NAV/*.png ./heli_nav_mean.pngПолучилась вот такая красота:

Видно виньетирование от большой диафрагмы и широкого угла, ногу, пыль на стекле, еще ногу, и тень от вертолета по центру.
Теперь возьмем вертикальную полосу откуда-нибудь из центра кадра и построим график яркости:
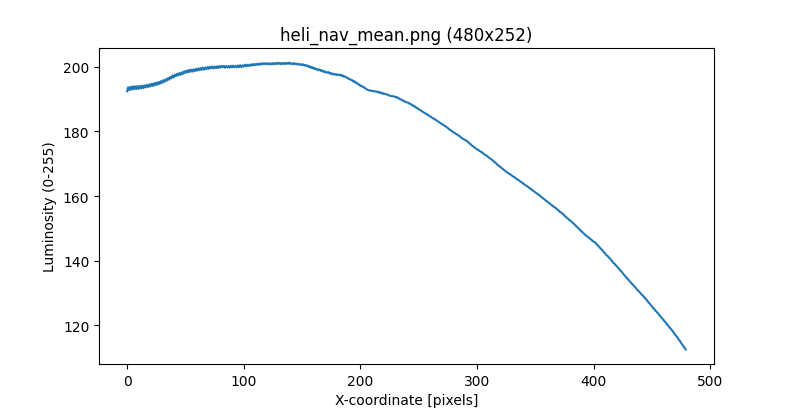
В центральной части (где не мешают искажения оптики и тень от вертолета) график более-менее линейный.
За 80 пикселей (360..280) яркость изменилась со 158 до 180. Или на (180-158)/158 ≈ 14%. 80 пикселей это 1/6 от полной высоты картинки, а значит PLS = 70/6/0.14 ≈ 83.
Можно снова взять что-нибудь среднее между 83 и 111: PLS ≈ 100 (или 99% эффективности затвора)
В данном случае эффект от PLS был так заметен только потому, что у нас есть быстро вращающиеся лопасти. Без них эффект выражался бы только в вертикальном градиенте яркости, который легко правится программно (с потерей динамического диапазона, но это не страшно).
3.8 Передний край
С градиентом понятно, но почему передний край на лопасти темнее, чем остальная часть?

В эксперименте со сложением двух фотографий пропеллера, мы упустили важную деталь: там пропеллер вращался быстро и успевал сделать много оборотов за время экспозиции, потому размазывался в аккуратный диск. Но с Ingenuity всё не так: за 9.3мс чтения лопасть проходит 140°. И это за полное время считывания. Для средних строк это будет уже 70°.
А если пропеллер не успевает сделать даже пол-оборота, тень от второй лопасти не дойдет до места, где была первая в момент начала экспозиции. А значит, тень не размажет в ровный круг, и то место откуда начала двигаться лопасть, будет светлее.
А то, что это заметно не на всех кадрах, объясняется вторым винтом: на 3 кадре угол между винтами около 22.5° и сектора, которые проходят лопасти за время засветки, полностью пересекаются, выравнивая яркость. А вот на двух первых кадрах угол >70° и винты не успевают долететь.

3.9 Ground truth
Можно ли проверить все эти домыслы, кроме как разглядывая фотографии с Ingenuity?
Я уже говорил, что подходящих камер у меня 0. Да и купить такую сейчас будет сложно — за 6 лет характеристики улучшились на порядки. К счастью, у нас есть ютуб, на котором иногда попадаются хорошие видео. Вот сегодняшнее хорошее видео:
(в комментах можно понаблюдать, как я упорно ничего не понимаю)
Это точно такая-же камера как на Ingenuity, снимающая быстро вращающийся пропеллер. Идеально!

И на видео отлично видно, что лопасти выглядят прозрачными. Гораздо более прозрачными, чем тени от вертолета, но тут и выдержка короче (77 а не 133), и сцена гораздо более контрастная.
3.10 Симуляция неэффективного затвора
Это всё еще не выглядит убедительно. Да, мы знаем что у глобального затвора есть засветка, и примерно представляем её величину для OV7251. Но хочется проверить.

Я набросал контуры винта и коробки с ногами, и нагуглил текстуру песочка.
Загружаем всё это безобразие в Pillow:
blade1 = Image.open("blade.png").convert("RGBA")
blade2 = blade1.transpose(Image.FLIP_TOP_BOTTOM)
box = Image.open("box.png").convert("RGBA")
background = Image.open("sand.jpg").convert("RGBA")
w,h = blade1.size
center = (w//2, h//2)
Trow = 19Trow здесь — время оцифровки одной строки изображения в микросекундах. Оно-же — минимальное время экспозиции. Оно-же — шаг времени для нашей симуляции.
Функция для экспонирования кадра за один Trow:
def single_exposure(cx, cy, scale, a1, a2, shadow_alpha, gain):
shape = blade1.rotate(a1, center=center)
t = blade2.rotate(a2, center=center)
shape.paste(t, (0,0), t)
shape.paste(box, (0,0), box)
if scale != 1:
shape = shape.resize((int(w*scale), int(h*scale)), Image.NEAREST)
data = np.array(shape)
r, g, b, a = data.T
black = (r == 0) & (g == 0) & (b == 0) & (a == 255)
data[..., :][black.T] = (0, 0, 0, shadow_alpha*255)
shape = Image.fromarray(data)
bg = background.copy()
bg.paste(shape, (int(w/2 - w*scale/2 + cx), int(h/2 - h*scale/2 + cy)), shape)
return np.array(bg.convert("L")) * gainТут я безуспешно пытаюсь совладать с Pillow, вращаю лопасти на углы a1 и a2, собираю лопасти и коробку вместе, масштабирую и перемещаю, делаю их немного прозрачными (чтобы тень не была совсем черной) и прилепляю на песочек. В конце умножаю всё на gain — коэффициент, который поможет нам в итоге получать нормальную экспозицию.
Как живой!
Теперь, функция, собирающая кадр. Мы можем разделить всё происходящее на три этапа:
-
Сама экспозиция: кадр с выдержкой длительностью exposure_us, за время которой лопасти успевают немного сдвинуться.
-
Ожидание перед считыванием. Теперь длительность hold_us, и учитывается PLS - кадр во много раз темнее.
-
Считывание кадра. Тут вещи становятся хитрыми. Первая строка проэкспонируется в течение 1 лишнего Trow, а потом прочитается. 480я строка - в течение 480 Trow, причем в это время положение лопастей будет заметно меняться. Так что для кадра в 480 строк нам придется наплодить 480 фреймов для того чтобы брать с них строки для симуляции PLS.
def construct_frame(exposure_us, RPM, PLS, a1, a2, readout_us=h*Trow,
shadow_alpha=0.6, gain=None, hold_us=0, cy=0, cx=0, scale=1):
degrees_per_trow = RPM/60E6*360*Trow
exposure_trows = exposure_us//Trow
hold_trows = hold_us//Trow
kReadout = readout_us/h/Trow
if gain==None:
gain = 1/(exposure_trows + hold_trows/PLS + (h/2)/PLS*kReadout) * gain_correction
sensor = np.zeros((w,h))
if exposure_us != 0:
print("Building Base image")
for i in progressbar(range(exposure_trows)):
sensor += single_exposure(cx, cy, scale, a1, a2, shadow_alpha, gain)
a1 += degrees_per_trow
a2 -= degrees_per_trow
if hold_trows != 0:
print("Building Hold image")
for i in progressbar(range(hold_trows)):
sensor += single_exposure(cx, cy, scale, a1, a2, shadow_alpha, gain) / PLS
a1 += degrees_per_trow
a2 -= degrees_per_trow
if readout_us != 0:
print("Applying PLS frames")
PLS_frames = []
for line in progressbar(range(h)):
PLS_frames.append(single_exposure(cx, cy, scale, a1 ,a2, shadow_alpha, gain) / PLS * kReadout)
for t in range(-1, -line-1, -1):
sensor[line,:] += PLS_frames[t][line,:]
a1 += degrees_per_trow * kReadout
a2 -= degrees_per_trow * kReadout
return Image.fromarray(np.uint8(np.clip(sensor, a_min=0, a_max=255)), 'L')readout_us и, получаемый из него, kReadout нужны чтобы симулировать разную скорость считывания. А устанавливая exposure_us, readout_us или hold_us в 0 можно отключать соответствующие компоненты кадра.
sensor - массив в котором мы суммируем все экспозиции. Как и в реальности, каждая часть процесса просто насыпает заряд в его ячейки.
gain выбирается так, чтобы в середине кадра (h/2) экспозиция была нормальной.
Проверим, как этот ужас работает:
construct_frame(exposure_us=133, RPM=2537, PLS=100,
readout_us=9272, a1=-35, a2=90).save("test.png")
Чтобы было удобнее перебирать разные параметры, я написал обертку, которой можно задавать варианты для каждого из них. Посмотрим, как размывает лопасти при разной выдержке (без учета PLS):
Выдержка меняется от 19 до 12000 микросекунд
Интересно, что размывает их не просто в диск, а с паттерном из 4х светлых полос, который отмечает места пересечения лопастей при вращении. В любой точке за время экспозиции пролетает 2 лопасти (в разные стороны), но в точках пересечения — они пролетают одновременно, перекрывая свет на в 2 раза меньшее время.
Теперь, посмотрим на эффект от PLS. Если взять PLS=100, то разное время чтения сенсора будет выглядеть вот так:
Время чтения сенсора меняется от 19 до 24000 миллисекунд
Видно, как при увеличении соотношения Чтение/Экспозиция, PLS всё больше влияет на картинку. Если присмотреться, то можно увидеть размазанный след от того, что за время чтения лопасти успели повернуться:

В верхней части они успели повернуться меньше, чем в нижней. Потому что нижние строки засвечивались дольше.
Скажем, что длительность чтения была 9.3мс и посмотрим, что будет если менять PLS:
На низких PLS градиент практически пересвечивает нижнюю часть кадра, а кроме прозрачных винтов заметны и следы от их движения за время чтения. На PLS порядка 100, градиент выравнивается до приличного уровня. Интересно, что даже на PLS 2500 можно разглядеть разницу в тенях между винтом и ногами.
Мы забыли про паузу между экспозицией и чтением. Скажем, что PLS=100, выдержка 133мкс, а чтение 9.3мс. Тогда:
Пауза при неизменной PLS и времени чтения, влияет на общую яркость, при этом уменьшая градиент.
А вот так выглядит отдельно эффект от PLS при разном времени чтения:
Я выбрал несколько кадров с вертолета и попробовал воспроизвести их.




Выглядит похоже. Хотя симуляция кажется несколько темнее (PLS слишком большой?) и с менее заметными градиентами на передней части лопастей (выдержка должна быть по-меньше?). Но в целом это вполне убедительно доказывает, что параметры примерно верные.
4. Постскриптум
Вот так, с помощью спичек, желудей и школьного учебника геометрии, можно изучать космическую технику не вставая с дивана.
Если бы мне 10 лет назад сказали, что на Марсе будет летать вертолет на солнечной батарейке, а марсоход будет снимать его на видео со звуком, я бы не поверил по целому набору причин.
Но вот мы здесь. Ingenuity, который создавался как proof-of-concept и не был обременен излишней консервативностью при выборе оборудования, таскает камеру с самым большим разрешением из всех что были на поверхности Марса и кучу легкой и компактной industrial-grade электроники.

На вертолете нет научного оборудования, кроме камер. Но зато он может моментально слетать за пол-километра и пофоткать со всех сторон очередной очень интересный камень.
Каждый новый полет сложнее предыдущего, но если МиМи не решит сделать бочку, нас ждет еще много материала от маленького марсианского вертолета.

Нет, вы только послушайте какая энергия у человека!
5. Ссылкография
https://github.com/dcoder-mm/heli-shadow-supplementary
Скрипты, видео и всякое прочее из статьи.
https://github.com/dcoder-mm/HELI_NAV
https://github.com/dcoder-mm/HELI_RTE_JPEG
Архивы фотографий с камер Ingenuity. Я прикручу автообновление, если будет не лень.
Марс и вертолеты
Mars Helicopter Technology Demonstrator PDF от вертолета. Довольно подробное описание железа, конструкции и испытаний от главного инженера проекта.
https://mars.nasa.gov/mars2020/multimedia/raw-images/ Всем известный каталог фотографий с марсохода и вертолета (архивы выше — оттуда).
https://forum.nasaspaceflight.com/index.php?topic=53277.0 API для него
https://archives.esac.esa.int/psa Чуть менее известный каталог от Европейского Космического Агентства, содержащий не только фото но и данные с инструментов. Там можно посмотреть, как Philae закатился в яму на комете и помер :(
https://mars.nasa.gov/technology/helicopter/status/298/what-were-learning-about-ingenuitys-flight-control-and-aerodynamic-performance/ Статья про то как летает вертолет на Марсе. С графиками и интересными подробностями.
https://mars.nasa.gov/technology/helicopter/status/ Статус апдейты вертолета.
https://en.wikipedia.org/wiki/Ingenuity_(helicopter)#List_of_flights Внезапно, википедия. Там отличная сводная таблица полетов с параметрами и описаниями.
https://mars.nasa.gov/rss/api/?feed=weather&category=mars2020&feedtype=json А это json с актуальной погодой на Марсе. Понятия не имею зачем, но сам факт!
Камеры
Даташит на OV7750, потому что она почти такая-же как OV7251. https://cdn.datasheetspdf.com/pdf-down/O/V/7/OV7750-OmniVision.pdf
https://datasheet.octopart.com/OV09716-B77Y-OE-Z-Omnivision-Technologies-datasheet-138897320.pdf Бумажка от OV9716. Да, тоже не та камера. Зато тут много подробностей которые общие для всех этих камер от Omnivision.
https://sst.semiconductor-digest.com/2014/09/global-shutter-image-sensors/ Сравнение разных архитектур глобальных затворов
https://www.imagesensors.org/Past%20Workshops/2013%20Workshop/2013%20Papers/Slides/12-1_Velichko_SLIDES.pdf Тоже сравнение разных архитектур, но в виде слайдов с картинками (отсюда был утащен график для PLS 2013 года)
https://www.imaging.org/Site/PDFS/Conferences/ElectroincImaging/EI2018/EI2017-IMSE-CIS_pixel_design_optimization_Boyd_v2.pdf И еще одна аналогичная презентация, от Omnivision
https://www.researchgate.net/publication/223133651_CMOS_Image_Sensors_for_High_Speed_Applications Хорошая, хоть и старая (2009) статья про высокоскоростные CMOS матрицы и их проблемы.
Комментариев нет:
Отправить комментарий