Новое доказательство за авторством австралийского писателя-фантаста Грега Игана и доказательство от 2011 года, анонимно опубликованное в сети, признали значительными прорывами в области изучения загадки, которую математики исследуют уже 25 лет

16 сентября 2011 года один фанат аниме опубликовал на форуме математический вопрос 4chan, касающийся культового сериала "Меланхолия Харухи Судзумии". Первый сезон шоу, где были и путешествия во времени, показали в порядке, отличном от хронологического, а во время дальнейшего показа и выпуска на DVD порядок эпизодов снова меняли. В интернете фанаты спорили о том, в каком порядке лучше смотреть сериал, а автор вопроса поинтересовался: если бы зрители захотели посмотреть сериал во всех возможных порядках, какое количество эпизодов было бы в кратчайшем их списке? [имеется в виду список, в котором можно найти любую последовательность эпизодов / прим. перев.]
Менее чем за час один аноним привёл ответ на вопрос – не полное решение, но нижнюю границу на необходимое количество эпизодов. Из его рассуждения, применимого к любому количеству эпизодов, следовало, что для первого сезона Харухи, состоявшего из 14 серий, зрителям пришлось бы посмотреть не менее 93 884 313 611 серий подряд, чтобы изучить все возможные перестановки. «Изучите доказательство на предмет недостатков, которые я мог бы пропустить», — написал автор ответа.
Доказательство семь лет оставалось незамеченным в математическом сообществе – оказалось, что в тот момент его заметил только один профессиональный математик, и он не изучил его достаточно тщательно. Однако внезапно в прошлом месяце австралийский писатель-фантаст Грег Иган доказал наличие нового верхнего предела на необходимое количество эпизодов. Открытие Игана заново подняло интерес к задаче и привлекло внимание к записи, касавшейся нижней границы, от 2011 года. Оба эти доказательства сейчас расцениваются как значительные прорывы в деле изучения загадки, которую математики исследуют не менее 25 лет.
Математики быстро проверили верхнюю границу от Игана, которая, как и нижняя граница, применима к последовательностям любой длины. Затем Робин Хьюстон, математик из компании Kiln, занимающейся визуализацией данных, и Джей Пэнтон из Университета Маркетта из Милуоки независимо подтвердили работу анонимного автора с 4chan. «Много усилий ушло на проверку правильности этой гипотезы», — сказал Пэнтон, поскольку ключевые идеи доказательства не были выражены достаточно чётко.
И теперь Хьюстон и Пэнтон, совместно с Винсом Вэтером из Флоридского университета написали формальную работу. В ней они указали первого автора как «анонимный постер 4chan».
«Странность ситуации в том, что это очень элегантное доказательство ранее неизвестного факта появилось в таком маловероятном месте», — сказал Хьюстон.
Города перестановок
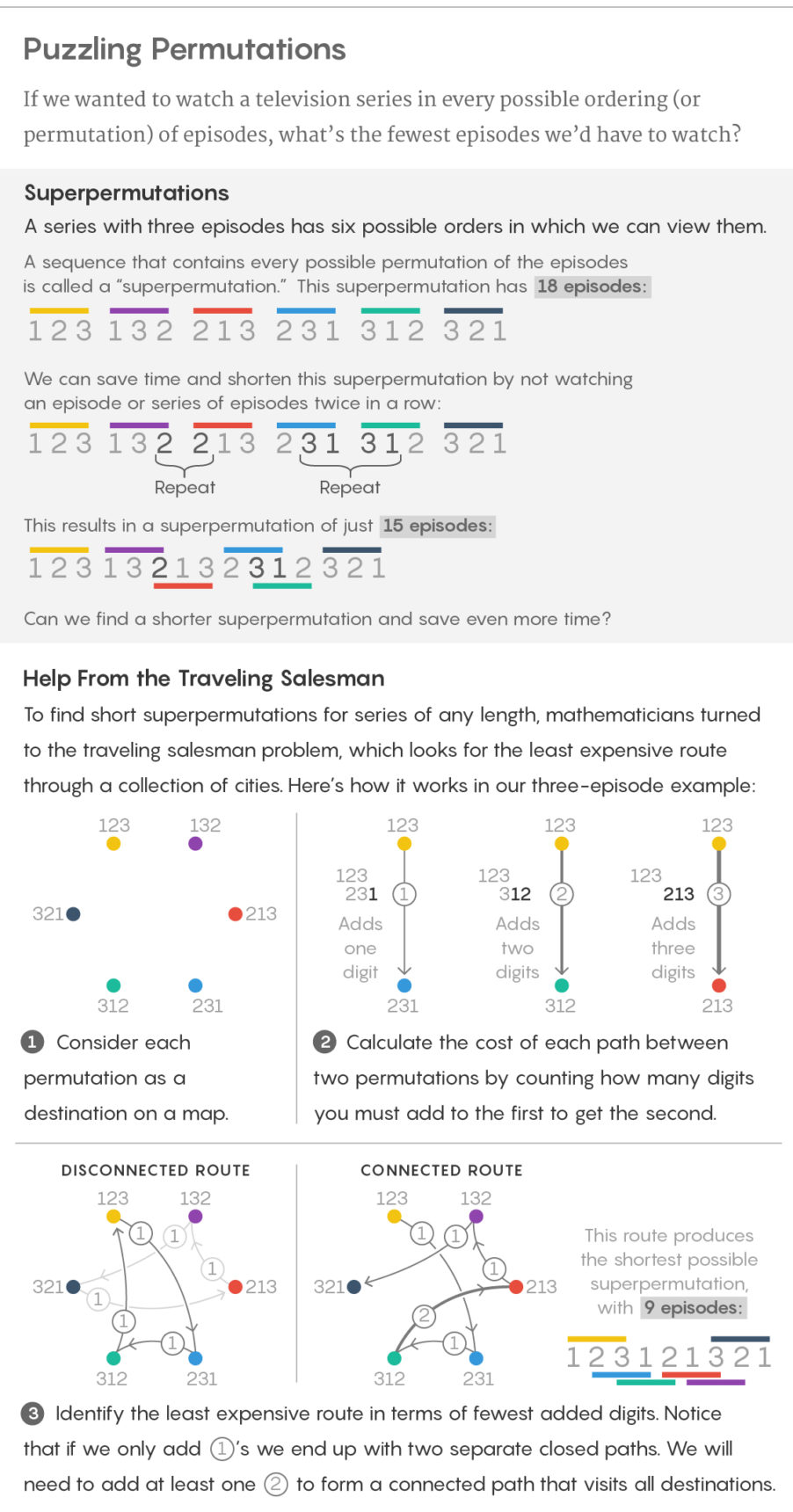
Если в сериале всего три эпизода, существует шесть возможных способов их посмотреть: 123, 132, 213, 231, 312 и 321. Их можно склеить вместе и сделать список из 18 эпизодов, включающих в себя каждый вариант порядка. Однако существует и более эффективный способ склейки: 123121321. Такая последовательность, содержащая все перестановки набора из n символов, называется сверхперестановкой.
В 1993 году Дэниел Эшлок и Дженет Тилотсон обнаружили, что при изучении кратчайших сверхперестановок для различных значений n быстро начинают проявляться факториалы – те же самые значения, записанные в виде n!, то есть, перемножения всех чисел от 1 до n (к примеру, 4! = 4 * 3 * 2 * 1).
Если в вашем сериале всего 1 эпизод, то длина кратчайшей сверхперестановки будет равна 1! (также известная, как старая добрая единица). Для сериала из двух эпизодов кратчайшая сверхперестановка (121) имеет длину 2! + 1!.. Для трёх эпизодов (пример выше) длина оказывается равной 3! + 2! + 1!, а для четырёх эпизодов (123412314231243121342132413214321) она будет 4! + 3! + 2! + 1!.. Правило факториалов стало общепринятым (хотя никто не мог доказать, что оно верно для всех n), и позже математики подтвердили его для n = 5.
Затем в 2014 году Хьюстон поразил математиков, показав, что для n = 6 правило перестаёт работать. Правило предсказывает, что для просмотра шести эпизодов всеми возможными способами потребуется 873 эпизода, но Хьюстон нашёл способ сделать это за 872. И поскольку существует простой способ превратить короткую сверхперестановку для n символов в короткую сверхперестановку для n+1 символов, пример Хьюстона означал, что правило факториалов не работает и для всех n > 6.
Построение Хьюстона превращает задачу сверхперестановки в знаменитую задачу коммивояжёра, которая ищет кратчайший путь через несколько городов. Конкретно, сверхперестановки связаны с «асимметричной» задачей коммивояжёра, в которой каждый путь между двумя городами имеет свою цену (не обязательно одинаковую в обоих направлениях), а целью является нахождение наиболее дешёвого пути через все города.
Это превращение легко понять: представим, что каждая перестановка – это город, и представим себе путь от каждой перестановки до каждой другой перестановки. В задаче сверхперестановки нам нужна кратчайшая последовательность цифр, в которой присутствуют все перестановки, поэтому нашей целью является пройти через все перестановки так, чтобы добавить к начальной перестановке как можно меньше чисел. Мы объявляем, что стоимость каждого пути просто равна количеству цифр, которое нам необходимо присоединить к концу первой перестановки, чтобы получить вторую. В примере с n = 3 путь от 231 до 312 стоит $1, поскольку нам нужно добавить только 2 к концу 231, чтобы получить 312, а путь от 231 до 132 стоит $2, поскольку нам надо добавить 32. В такой формулировки наиболее дешёвый путь через все города напрямую соответствует кратчайшей сверхперестановке.
Такое превращение означало, что Хьюстон мог направить все возможности алгоритмов решения задачи коммивояжёра на задачу сверхперестановки. Эта задача известна своей принадлежностью к классу NP-сложных, что означает отсутствие существования эффективного алгоритма, способного решать её в общем случае. Однако существуют алгоритмы, способные эффективно решать некоторые разновидности задачи, а другие алгоритмы могут выдавать неплохие примерные решения. Хьюстон использовал один из последних, чтобы выдать сверхперестановку длиной в 872 цифры.
Поскольку он выдал лишь приблизительное решение, оно даже может быть не самой идеальной сверхперестановкой. Математики сейчас проводят объёмный вычислительный поиск кратчайшей сверхперестановки из 6 символов, сказал Пэнтон. «Мы знаем, что наши поиски закончатся за конечное время, но не знаем, займёт это неделю или миллион лет, — сказал он. – Индикатора выполнения там нет».
Неправильный порядок
К моменту появления работы Хьюстона, анонимный пост на 4chan сидел в своём уголке интернета почти три года. Один математик, Натаниэль Джонстон из Университета Маунт-Эллисон, заметил копию этого поста на другом сайте через несколько дней после того, как эта запись появилась – и не потому, что он был любителем аниме, но потому, что он вводил в Google разные запросы, связанные с сверхперестановками.
Джонстон прочитал доказательство и оно показалось ему достоверным, но он не стал тратить силы на тщательную проверку. В то время математики считали, что формула факториалов для сверхперестановок была, скорее всего, верной, и когда вы считаете, что вам известен точный ответ на вопрос, нижняя граница оценки вас интересует слабо. Иначе говоря, эпизоды сериала про сверхперестановки шли не в том порядке.
После этого Джонстон упоминал нижнюю границу на паре веб-сайтов, но «я не думаю, что кто-то обратил на это особое внимание», — сказал он.
Затем 26 сентября 2018 математик Джон Баез из Калифорнийского университета в Риверсайде опубликовал в твиттере пост по поводу открытия Хьюстона от 2014 года, в рамках серии твитов по поводу очевидных математических закономерностей, которые перестают работать.
Прим. перев.: там была не такая уж большая серия твитов, всего три. Два остальных тоже интересны сами по себе, хотя не имеют отношения к данной статье. В одном говорится о том, что 6 – это самое популярное расстояние между двумя соседними простыми числами для всех простых чисел меньших, чем 17 427 000 000 000 000 000 000 000 000 000. А потом эта закономерность вдруг перестаёт работать! Второе демонстрирует следующую связь интегралов, тригонометрических функций и числа π

Но только для n < 9,8 × 1042!
Его твит привлёк внимание Игана, изучавшего математику несколько десятилетий назад, до того, как началась его карьера признанного писателя-фантаста (его первая успешная повесть, по счастливой случайности, называлась «Город перестановок»). «Я никогда не переставал интересоваться математикой», — написал Иган по почте.
Иган заинтересовался, возможно ли создать сверхперестановку ещё более короткую, чем у Хьюстона. Он погрузился в изучение литературы о том, как создавать короткие пути в сетях перестановок, и через несколько недель нашёл то, что ему требовалось. За пару дней он вывел новую верхнюю границу на длину кратчайшей сверхперестановки из n символов: n! + (n – 1)! + (n – 2)! + (n – 3)! + n – 3. Она похожа на формулу факториалов, из которой исключили много членов.
«Это полностью разбило предыдущую верхнюю границу», — сказал Хьюстон.
Нижняя граница автора поста на 4chan была соблазнительно близка к новой верхней границе: n! + (n – 1)! + (n – 2)! + n – 3. После публикации результата Игана Джонстон напомнил математикам о доказательстве анонимного автора, и Хьюстон с Пэнтоном вскоре доказали его корректность. Как и в работе Хьюстона, новая нижняя и верхняя границы подходят к сверхперестановкам с точки зрения задачи коммивояжёра: нижняя граница показывает, что путь через все города должен пройти через некоторое минимальное количество путей стоимостью более $1, а верхняя граница создаёт особый путь для каждого n, использующий только соединения стоимостью в $1 и $2.
Теперь исследователи пытаются свести верхнюю и нижнюю границы вместе, и найти единую формулу, решающую задачу сверхперестановки. «Вероятно, в итоге люди всё же разгадают это загадку, — предсказал Баез. – Сейчас уже всё выглядит неплохо».
Для фанатов Харухи решение Игана даёт точную инструкцию о том, как просмотреть все возможные варианты порядка первого сезона, используя всего 93 924 230 411. Начинать просмотр можно уже сегодня, или можно подождать, пока математики смогут ещё урезать это число. Нижняя граница от анонимного автора доказывает, что это урезание не сможет сэкономить им больше 40 млн эпизодов – однако, этого достаточно, чтобы начать готовиться ко второму сезону.
Комментариев нет:
Отправить комментарий