0, 0, 1, 0, 2, 0, 2, 2, 1, 6, 0, 5, 0, 2, 6, 5, 4, 0, 5, 3, 0, 3, 2, 9, 0, 4, 9, 3, 6, 14, 0, 6, 3, 5, 15, 0, 5, 3, 5…

Есть два мужика с именами «Van Eck». Первый, в 1985 году показал всему миру как за 15 долларов перехватывать данные с монитора (Van Eck phreaking), второй, в 2010 придумал хитрую последовательность (Van Eck's sequence). Круче простоты задания этой последовательности могут быть только её свойства и загадки.

Итак, алгоритм генерации членов последовательности. Берем «стартовое число», например «0», выписываем. Следующий член — это то, сколько шагов назад встречалось это число в предыдущей под-последовательности. Если ни разу, то пишем ноль. Следующее — это сколько шагов назад встречался ноль в предыдущей под-последовательности, то есть один шаг назад. Записываем единицу. Единица впервые — пишем ноль. Опа, ноль встречался два шага назад. Пишем два, и так далее…

Для точки отчета «0» первые 97 членов последовательности:
0, 0, 1, 0, 2, 0, 2, 2, 1, 6, 0, 5, 0, 2, 6, 5, 4, 0, 5, 3, 0, 3, 2, 9, 0, 4, 9, 3, 6, 14, 0, 6, 3, 5, 15, 0, 5, 3, 5, 2, 17, 0, 6, 11, 0, 3, 8, 0, 3, 3, 1, 42, 0, 5, 15, 20, 0, 4, 32, 0, 3, 11, 18, 0, 4, 7, 0, 3, 7, 3, 2, 31, 0, 6, 31, 3, 6, 3, 2, 8, 33, 0, 9, 56, 0, 3, 8, 7, 19, 0, 5, 37, 0, 3, 8, 8, 1

График:

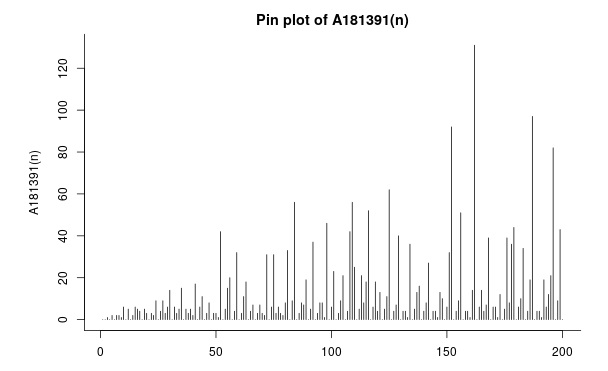
Еще больше график:

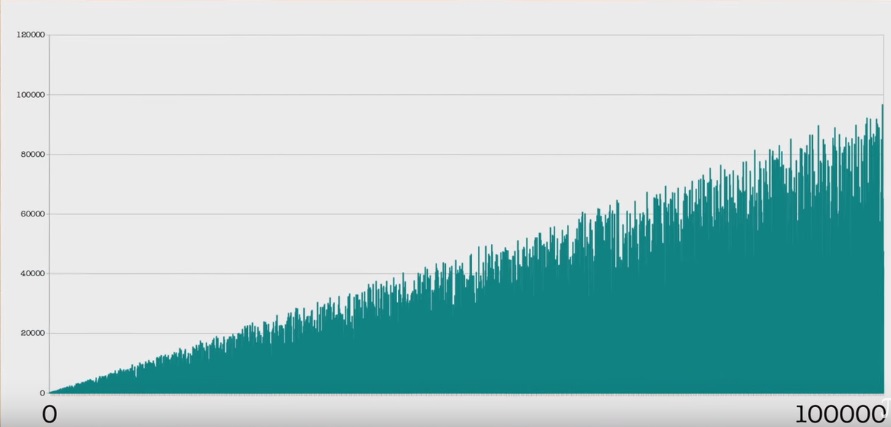
Довольно легко доказываются свойства последовательности, что её максимальный член все время возрастает и что в ней бесконечное количество нулей. Или что в ней нет периодов. (Несколько теорем и следствий тут.)

Логарифмический график:

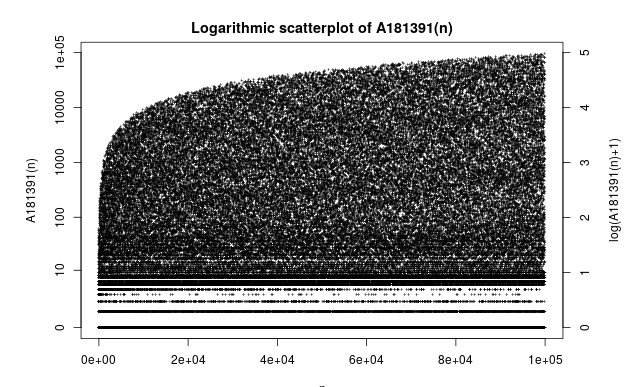
Прога на Python:

A181391 = [0]

last_pos = {}

for i in range(10**4):

    new_value = i - last_pos.get(A181391[i], i)

    A181391.append(new_value)

    last_pos[A181391[i]] = i

# Ehsan Kia, Jun 12 2019

Для стартового числа «1» первая сотня такая:

1, 0, 0, 1, 3, 0, 3, 2, 0, 3, 3, 1, 8, 0, 5, 0, 2, 9, 0, 3, 9, 3, 2, 6, 0, 6, 2, 4, 0, 4, 2, 4, 2, 2, 1, 23, 0, 8, 25, 0, 3, 19, 0, 3, 3, 1, 11, 0, 5, 34, 0, 3, 7, 0, 3, 3, 1, 11, 11, 1, 3, 5, 13, 0, 10, 0, 2, 33, 0, 3, 9, 50, 0, 4, 42, 0, 3, 7, 25, 40, 0, 5, 20, 0, 3, 8, 48, 0, 4, 15

График:

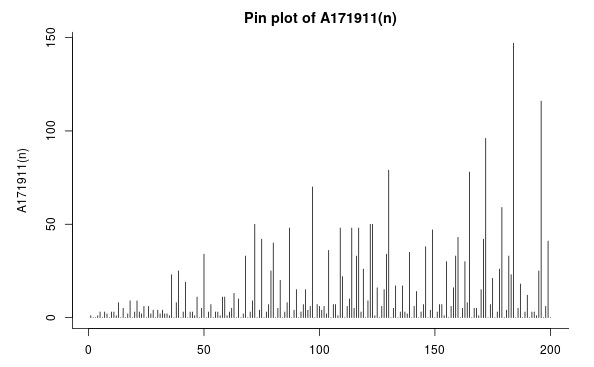
Для стартового числа «2» первая сотня такая:

2, 0, 0, 1, 0, 2, 5, 0, 3, 0, 2, 5, 5, 1, 10, 0, 6, 0, 2, 8, 0, 3, 13, 0, 3, 3, 1, 13, 5, 16, 0, 7, 0, 2, 15, 0, 3, 11, 0, 3, 3, 1, 15, 8, 24, 0, 7, 15, 5, 20, 0, 5, 3, 12, 0, 4, 0, 2, 24, 14, 0, 4, 6, 46, 0, 4, 4, 1, 26, 0, 5, 19, 0, 3, 21, 0, 3, 3, 1, 11, 42, 0, 6, 20, 34, 0, 4, 20, 4

График:

Источники

Let's block ads! (Why?)