Идти будем маленькими шагами: сначала вспомним, как загружать данные в Python, затем научимся считать слова, постепенно подключим линейную алгебру и теорвер, и под конец сделаем из получившегося болтательного алгоритма бота для Телеграм.
Этот туториал подойдёт тем, кто уже немножко трогал пальцем Python, но не особо знаком с машинным обучением. Я намеренно не пользовался никакими nlp-шными библиотеками, чтобы показать, что нечто работающее можно собрать и на голом sklearn.
Поиск ответа в диалоговом датасете
Год назад меня попросили показать ребятам, которые прежде не занимались анализом данных, какое-нибудь вдохновляющее приложение машинного обучения, которое можно собрать самостоятельно. Я попробовал собрать вместе с ними бота-болталку, и у нас это действительно получилось за один вечер. Процесс и результат нам понравились, и написал об этом в своем блоге. А теперь подумал, что и Хабру будет интересно.
Итак, начинаем. Наша задача — сделать алгоритм, который на любую фразу будет давать уместный ответ. Например, на «как дела?» отвечать «отлично, а у тебя?». Самый простой способ добиться этого — найти готовую базу вопросов и ответов. Например, взять субтитры из большого количества кинофильмов.
Я, впрочем, поступлю ещё более по-читерски, и возьму данные из соревнования Яндекс.Алгоритм 2018 — это те же диалоги из фильмов, для которых работники Толоки разметили хорошие и неплохие продолжения. Яндекс собирал эти данные, чтобы обучать Алису (статьи о её кишках 1, 2, 3). Собственно, Алисой я и был вдохновлен, когда придумывал этого бота. В таблице от Яндекса даны три последних фразы и ответ на них (reply), но мы будем пользоваться только самой последней из них (context_0).
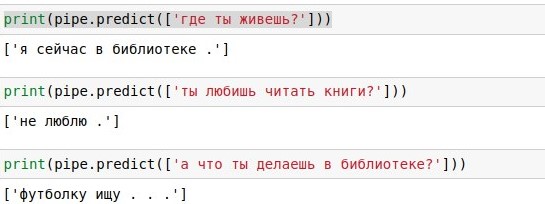
Имея такую базу диалогов, можно просто искать в ней каждую реплику пользователя, и выдавать готовый ответ на ней (если таких реплик много, выбирать случайно). С «как дела ?» такое отлично получилось, о чём свидетельствует приложенный скриншот. Это, если что, jupyter notebook на Python 3. Если вы хотите повторить такое сами, проще всего установить Анаконду — она включает Python и кучу полезных пакетов для него. Или можно ничего не устанавливать, а запустить блокнот в гугловском облаке.

Проблема дословного поиска в том, что у него низкое покрытие. На фразу «как твои дела ?» в базе из 40 тысяч ответов точного совпадения не нашлось, хотя смысл у неё тот же самый. Поэтому в следующем разделе мы будем дополнять наш код, применяя разную математику, чтобы реализовать приближённый поиск. А перед этим вы можете почитать про библиотеку pandas и разобраться, что же делает каждая из 6 строк вышеприведённого кода.
Векторизация текстов
Теперь говорим о том, как превратить тексты в числовые векторы, чтобы осуществлять по ним приближённый поиск.
Мы уже познакомились с библиотекой pandas в Python — она позволяет загружать таблицы, осуществлять поиск в них, и т.п. Теперь затронем библиотеку scikit-learn (sklearn), которая позволяет более хитрые манипуляции с данными — то, что называется машинным обучением. Это значит, что любому алгоритму сперва нужно показать данные (fit), чтобы он узнал о них что-то важное. В результате алгоритм «научится» делать с этими данными что-то полезное — преобразовывать их (transform), или даже предсказывать неизвестные величины (predict).
В данном случае мы хотим преобразовать тексты («вопросы») в числовые векторы. Это нужно, чтобы можно было находить «близкие» друг к другу тексты, пользуясь математическим понятием расстояние. Расстояние между двумя точками можно рассчитать по теореме Пифагора — как корень из суммы квадратов разностей их координат. В математике это называется Евклидовой метрикой. Если мы сможем превращать тексты в объекты, у которых есть координаты, то мы сможем вычислять Евклидову метрику и, например, находить в базе вопрос, наиболее всего похожий на «о чём ты думаешь?».
Самый простой способ задать координаты текста — это пронумеровать все слова в языке, и сказать, что i-тая координата текста равна числу вхождений в него i-того слова. Например, для текста «я не могу не плакать» координата слова «не» равна 2, координаты слов «я», «могу» и «плакать» равны 1, а координаты всех остальных слов (коих десятки тысяч) равны 0. Такое представление теряет информацию о порядке слов, но всё равно работает неплохо.
Проблема в том, что у слов, которые встречаются часто (например, частиц «и» и «а») координаты будут несоразмерно большие, хотя информации они несут мало. Чтобы смягчить эту проблему, координату каждого слова можно поделить на логарифм числа текстов, где такое слово встречается — это называется tf-idf и тоже работает неплохо.

Проблема только одна: в нашей базе 60 тысяч текстовых «вопросов», в которых содержится 14 тысяч различных слов. Если превратить все вопросы в векторы, получится матрица 60к*14к. Работать с такой не очень классно, поэтому дальше мы поговорим о сокращении размерности.
Сокращение размерности
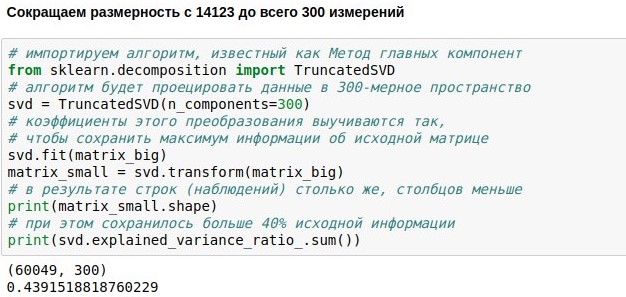
Мы уже поставили задачу создания болталочного чатбота, скачали и векторизовали данные для его обучения. Теперь у нас есть числовая матрица, представляющая реплики пользователей. Она состоит из 60 тысяч строк (столько было реплик в базе диалогов) и 14 тысяч столбцов (столько в них было различных слов). Сейчас наша задача — сделать её поменьше. Например, представить каждый текст не 14123-мерным, а всего лишь 300-мерным вектором.
Достичь этого можно, умножив нашу матрицу размера 60049х14123 на специально подобранную матрицу проекции размера 14123х300, в итоге получим результат 60049х300. Алгоритм PCA (метод главных компонент) подбирает матрицу проекции так, чтобы исходную матрицу можно было потом восстановить с наименьшей среднеквадратической ошибкой. В нашем случае получилось сохранить около 44% об исходной матрице, хотя размерность сократилась почти в 50 раз.
За счёт чего возможно такое эффективное сжатие? Напомним, что исходная матрица содержит счётчики упоминания отдельных слов в текстах. Но слова, как правило, употреблятся не независимо друг от друга, а в контексте. Например, чем больше раз в тексте новости встречается слово «блокировка», тем больше раз, скорее всего в этом тексте встретится также слово «телеграм». А вот корреляция слова «блокировка», например, со словом «кафтан» отрицательная — они встречаются в разных контекстах.
Так вот, получается, что метод главных компонент запоминает не все 14 тысяч слов, а 300 типовых контекстов, по которым эти слова потом можно пытаться восстановить. Столбцы матрицы проекции, соответствующие синонимичным словам, обычно похожи друг на друга, потому что эти слова часто встречаются в одном контексте. А значит, можно сократить избыточные измерения, не потеряв при этом в информативности.
Во многих современных приложениях матрицу проекции слов вычисляют нейросети (например, word2vec). Но на самом деле простой линейной алгебры для практически полезного результата уже достаточно. Метод главных компонент вычислительно сводится к SVD, а оно — к расчёту собственных векторов и собственных чисел матрицы. Впрочем, программировать это можно, даже не зная деталей.
Поиск ближайших соседей
В предыдущих разделах мы закачали в python корпус диалогов, векторизовали его, и сократили размерность, а теперь хотим наконец научиться искать в нашем 300-мерном пространстве ближайших соседей и наконец-то осмысленно отвечать на вопросы.
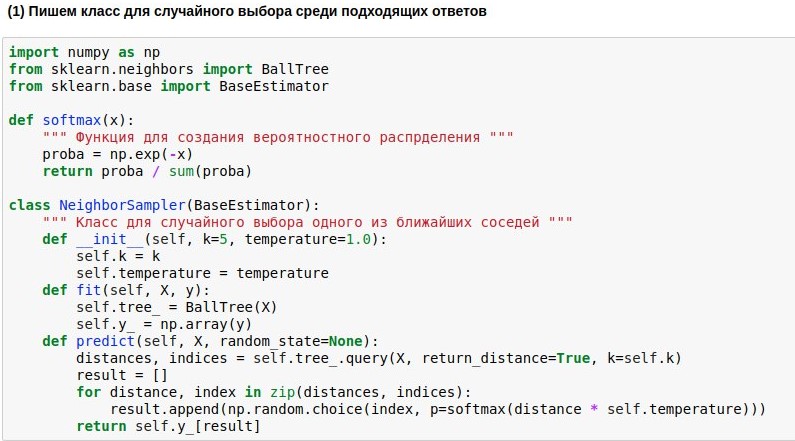
Поскольку научились отображать вопросы в Евклидово пространство не очень высокой размерности, поиск соседей в нём можно осуществлять довольно быстро. Мы воспользуемся уже готовым алгоритмом поиска соседей BallTree. Но мы напишем свою модель-обёртку, которая выбирала бы одного из k ближайших соседей, причём чем ближе сосед, тем выше вероятность его выбора. Ибо брать всегда одного самого близкого соседа — скучно, но не завязываться на сходство совсем — опасно.
Поэтому мы хотим превратить найденные расстояния от запроса до текстов-эталонов в вероятности выбора этих текстов. Для этого можно использовать функцию softmax, которая ещё часто стоит на выходе из нейросетей. Она превращает свои аргументы в набор неотрицательных чисел, сумма которых равна 1 — как раз то, что нам нужно. Дальше полученные «вероятности» мы можем использовать для случайного выбора ответа.
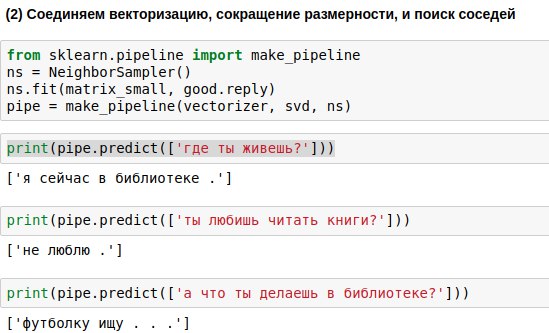
Фразы, которые будет вводить пользователь, надо пропускать через все три алгоритма — векторизатор, метод главных компонент, и алгоритм выбора ответа. Чтобы писать меньше кода, можно связать их в единую цепочку (pipeline), применяющую алгоритмы последовательно.
В результате мы получили алгоритм, который по вопросу пользователя способен найти похожий на него вопрос и выдать ответ на него. И иногда это ответы даже звучат почти осмысленно.
Публикация бота в Telegram
Мы уже разобрались, как сделать чатбота-болталку, который бы выдавал примерно уместные ответы на запросы пользователя. Теперь показываю, как выпустить такого чатбота в Телеграм.
Проще всего использовать для этого готовую обёртку Telegram API для питона — например, pytelegrambotapi. Итак, пошаговая инструкция:
1) Регистрируете своего будущего бота в @botfather и получаете токен доступа, который вам надо будет вставить в свой код.
2) Разово запускаете команду установки — pip install pytelegrambotapi в командной строке (или через! прям в блокноте)
3) Запускаете код примерно как в скриншоте. Ячейка перейдёт в режим исполнения (*), и пока она будет в этом режиме, вы сможете общаться со своим ботом сколько захотите. Чтобы остановить бота, жмите Ctrl+C
4) Если вы хотите, чтобы бот работал перманентно, вам надо выложить его код на какой-нибудь облачный сервис — например, AWS, Heroku, now.sh или Яндекс.Облако. О том, как запустить их, вы можете узнать в мельчайших подробностях на сайтах этих сервисов или в статьях тут же на Хабре. Вот, например, репа с небольшим примером бота, запускаемого на heroku и кладущего логи в mongodb.
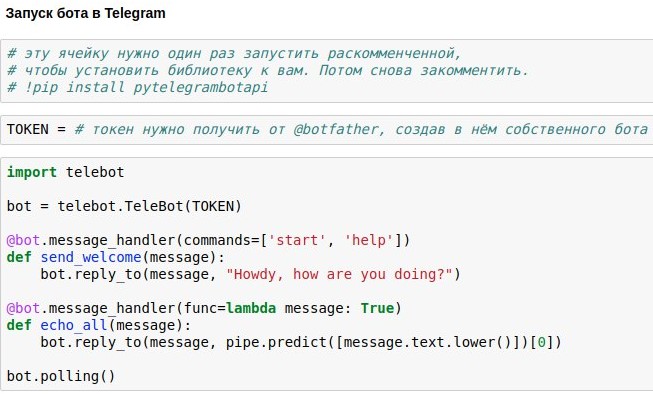
Полный код к статье я намеренно не выкладываю — вы получите гораздо больше удовольствия и полезного опыта, когда напечатаете его сами, и получите работающего бота в результате собственных усилий. Ну или если вам очень лень это делать, можете поболтать с моей версией ботика.
Комментариев нет:
Отправить комментарий