2 в 1: шифрование с имитозащитой

Классическими задачами, которые решаются криптографическими методами, являются обеспечение конфиденциальности и обеспечение аутентичности/имитостойкости хранимых и передаваемых данных. Ранее (примерно до середины 2000-х годов) для решения подобных задач использовались шифрование (конфиденциальность) и функции выработки имитовставки/кодов аутентификации (имитостойоксть). При этом шифрование и функция выработки имитовставки реализовывались отдельными криптографическими механизмами, что вызывало много проблем. В первую очередь, это связано с управлением ключевой информацией: при использовании одного ключа для шифрования и имитозащиты ряд схем, например, AES-CBC + AES-CBC-MAC являются полностью нестойкими. Для того, чтобы сделать такие конструкции безопасности приходится вырабатывать дополнительные ключи используя, например, функции выработки производных ключей (KDF). Это, в свою очередь, зачастую приводит к сильному усложнению криптографических протоколов, использующих подобные схемы. Кроме этого, последовательное использование двух механизмов не всегда является самым быстрым решением с точки зрения производительности.

С начала XXI века начались попытки создать механизмы шифрования с имитозащитой (иногда можно встретить термин «аутентифицированное шифрование» — от английского Authenticated Encryption), которые бы решали сразу обе указанные задачи.
Следующей ступенью развития таких механизмов можно считать механизмы шифрования с имитозащитой и ассоциированными данными (от англ. AEAD — Authenticated Encryption with Associated Data). Особенностью AEAD-механизмов является то, что они одновременно могут обрабатывать данные двух типов: данные, для которых необходимо обеспечить конфиденциальность и имитозащиту (например, данные IP-пакета), и данные, для которых необходимо обеспечить только имитозащиту без конфиденциальности – их еще называют «дополнительно имитозащищаемые данные» («ассоциированные данные», «дополнительно аутентифицируемые данные» — это может быть заголовок IP-пакета). Одной из наиболее востребованных областей применения AEAD-механизмов являются различные криптографические протоколы защиты данных, например, недавно принятый IETF TLS 1.3 RFC 8446, о чем уже писали на Хабре. Так вот, этот RFC 8446 рассматривает в качестве используемых в протоколе алгоритмы аутентифицированного шифрования (о принципах, лежащих в основе протокола TLS 1.3, можно почитать тут).

Строиться AEAD-механизмы могут на основе различных конструкций: поточные и блочные шифры, сжимающие отображения (хэш-функции), популярные сейчас конструкции типа «губка» (от англ. «sponge»). Разнообразие вариантов можно посмотреть, в частности, на сайте конкурса CAESAR и в различных обзорах про этот конкурс, см. например здесь и здесь. Кстати, сам конкурс был организован в 2013 году как раз с целью определения лучшего AEAD-механизма взамен широко используемого AES-GCM (режим GCM стандартизован NIST в 2007 году), для которого на тот момент был предложен ряд атак (вот и вот). При этом, к участникам конкурса CAESAR были предъявлены дополнительные функциональные требования, такие как возможность работы «онлайн», возможность распараллеливания, свобода от инверсий, защита от некорректного использования инициализационных и одноразовых векторов, наличие предвычислений, инкрементация данных, промежуточные имитовставки, повторное использование фиксированных ассоциированных данных. Поясним подробнее.

Работа «онлайн»: зачастую для обеспечения конфиденциальности/имитостойкости требуется сначала сформировать полностью весь пакет данных, который будет обрабатываться, а только потом начать процедуру обработки. Механизмы, допускающие работу «онлайн», этого не требуют, они могут работать с поступающим в режиме реального времени потоком данных, обрабатывая его «на лету». Под распараллеливанием AEAD-механизмов понимается возможность распределения вычислений между несколькими процессорами. Под свободой от инверсий понимается использование в AEAD-механизме только функции зашифрования или только функции расшифрования. Эта характеристика важна с точки зрения реализации: для некоторых шифров (как, например, Кузнечик, AES) – шифрование и расшифрование реализуются с помощью разных преобразований, соответственно, свобода от инверсий означает меньшую площадь кристалла при аппаратных реализациях или меньший объем программного кода при программной. С предвычислениями все просто – это возможность после выбора ключа провести ряд предварительных вычислений, которые в дальнейшем ускорят обработку поступающих данных.

Инкрементацию данных и повторное использование фиксированных ассоциированных данных в некотором смысле тоже можно отнести к предвычислениям. Под инкрементацией понимается возможность быстро пересчитать имитовставку, в случае если к уже обработанным данным мы добавили некоторые дополнительные данные, без повторной обработки всех данных. Использование фиксированных ассоциированных данных – это возможность выполнить предвычисления для часто встречаемых данных, чтобы каждый раз, когда они появляются, заново их не обрабатывать. Последнее свойство (промежуточные имитовставки) – это, в некотором смысле, тоже работа «на лету», т.е. возможность проверки на принимающей стороне корректности данных в процессе их обработки, не дожидаясь окончания передачи. Таким образом, если проверка промежуточной имитовставки не пройдет, весь последующий поток данных не требуется обрабатывать, и это экономит время и ресурсы.

Как оказалось, создать AEAD-механизм, одновременно удовлетворяющий такому широкому спектру требований, крайне сложно. Это привело к тому, что конкурс CAESAR неоднократно продлевался, дедлайны переносились, поскольку жюри не могло выбрать победителя – все участники обладали различными наборами свойств – и закончилось с оревнование только лишь весной 2019 года выбором нескольких участников с различными свойствами.

Прообраз отечественного AEAD-режима, впоследствии названого MGM (Multi Linear Galois Mode), впервые был представлен в 2017 г. MGM является режимом работы блочного шифра. Режим состоит из двух частей, каждая из которых основывается на своем счетчике. Первый счетчик используется для выработки последовательности, которая далее используется для шифрования. Принцип работы схож со счетчиком режима CTR (см. ГОСТ Р 34.13-2015 или ISO/IEC 10116), однако имеет существенное отличие: первоначальное значение счетчика получается с помощью шифрования из уникального вектора инициализации (nonce). Второй счетчик используется для построения мультилинейной функции, на основе которой вырабатывается имитовставка. Первый и второй счетчики работают по разному, первый инкрементирует правую половину блока, а второй — левую. Схема работы режима представлена на рисунке.

Здесь $$ — произвольный блочный шифр с длиной блока $$ бит, $$ — блоки ассоциированных данных, $$ — блоки открытого текста, $$ — уникальный вектор инициализации длины $$ бит, $$ — операция побитового сложения, $$ — операция умножения в поле $$, $$ — усечение блока длины до длины $$, $$ — длина в битах ассоциированных данных и шифртекста соответственно, $$ — функции инкрементирования.

В докладе и в статье можно найти подробное описание принципов построения режима MGM. Если коротко, то при разработке решалась следующая задача: создать функциональный и хорошо распараллеливаемый режим работы блочных шифров, который был бы не подвержен известным атакам, в частности, атакам, успешно применимым к режиму GCM. В упомянуты докладе показаны следующие функциональные возможности режима:

• распараллеливание,
• работа онлайн,
• отсутствие инверсий,
• возможность работы только для выработки имитовставки (т.е. без шифрования, по сути в данном случае MGM становится режимом выработки имитовставки),
• использование одного ключа для шифрования и аутентификации,
• использование уникального вектора инициализации (вместо (псевдо)случайного),
• возможность предвычислений.

В отличие от многих используемых в настоящее время режимов, для MGM удалось получить формальное обоснование стойкости в модели так называемой доказуемой стойкости (provable security), которое может быть резюмировано в виде двух теорем, оценивающих безопасное число блоков открытого текста, допустимых для обработки с помощью режима MGM без смены ключа. Пожалеем читателей и приведем здесь только их формулировки, желающие посмотреть полное доказательство и хорошенько проплавить мозги могут обратиться к исходной публикации. Первая теорема говорит об обеспечении конфиденциальности информации.

Теорема

Преимущество противника в задаче нарушения конфиденциальности, делающего не более $$ запросов к оракулу, общей длины открытого текста и ассоциированных данных не более $$ блоков, оценивается следующим неравенством:

$$

Вторая — о безопасности аутентификации данных (их имитостойкости).

Теорема

Преимущество противника в задаче нарушения имитостойкости, делающего не более $$ запросов к оракулу, общей длины открытого текста и ассоциированных данных не более $$ блоков, и выдающего подделку общей длины шифртекста и ассоциированных данных не более $$ блоков, оценивается следующим неравенством:

$$

Заметим, что при использовании подхода «доказуемой стойкости» всегда возникает вопрос о точности полученных оценок (т.е. насколько они на самом деле соответствуют действительности и адекватны практике). Так вот в данном случае они оказались точными, что подтвердили результаты работы, в которой указаны теоретические атаки для режима MGM в случае, если объем материала не удовлетворяет приведенным теоремам.

В таблице далее представлено сравнение разработанного режима с финалистами конкурса CAESAR по указанным выше характеристикам.

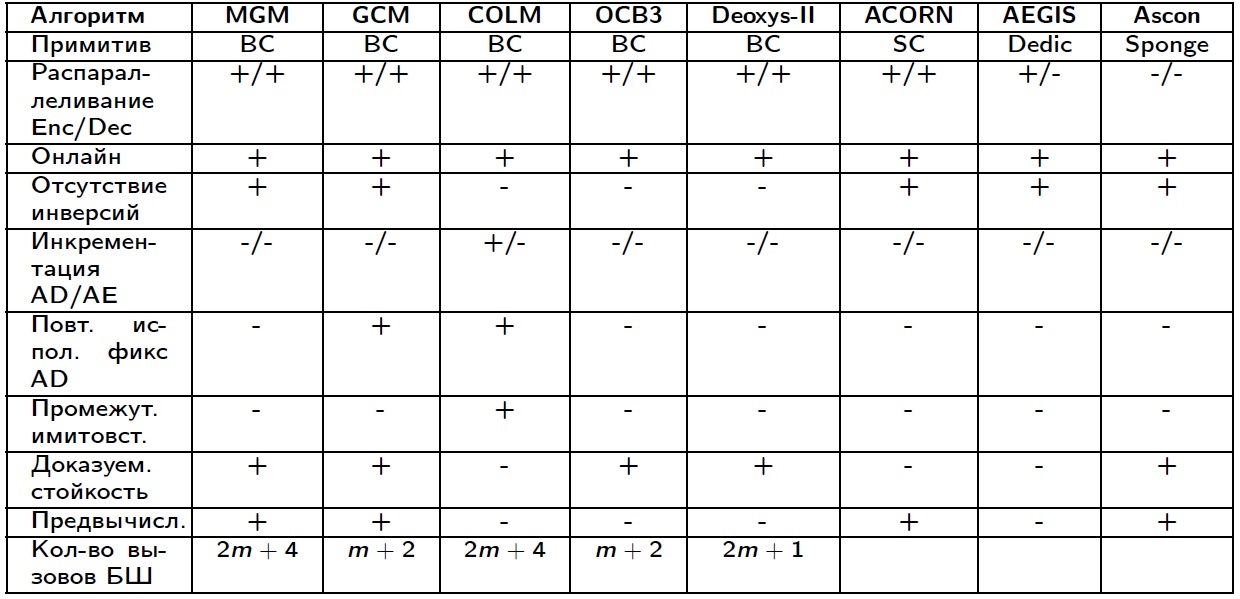
В таблице в качестве используемого примитива: обозначены BC — блочный шифр, SC — поточный шифр, Dedic — оригинальная конструкция (не использует шифр), Sponge — использует губку.

Как можно видеть, удалось разработать режим, удовлетворяющий достаточно большому набору эксплуатационных требований, и, что крайне важно, получить для него формальное обоснование стойкости.

В сентябре прошлого года Росстандарт утвердил режим MGM в рекомендациях по стандартизации Р 1323565.1.026–2019 «Информационная технология. Криптографическая защита информации. Режимы работы блочных шифров, реализующие аутентифицированное шифрование». Кроме того, в начале этого года организацией IANA были выделены идентификаторы, а Росстандартом были приняты рекомендации по стандартизации Р 1323565.1.030-2020 «Информационная технология. Криптографическая защита информации. Использование криптографических алгоритмов в протоколе безопасности транспортного уровня (TLS 1.3)» для использования российских криптоалгоритмов в протоколе TLS 1.3, — и как раз с применением режима MGM.

Let's block ads! (Why?)